3.4 实际问题与一元一次方程专题复习
文档属性
| 名称 | 3.4 实际问题与一元一次方程专题复习 |  | |
| 格式 | zip | ||
| 文件大小 | 565.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-18 13:03:56 | ||
图片预览









文档简介
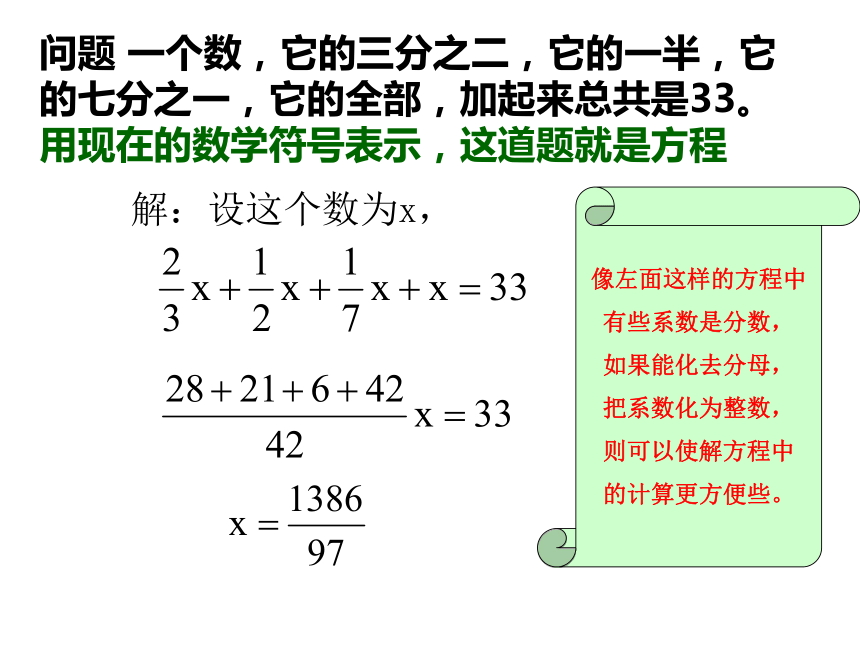
课件40张PPT。一元一次方程应用题专题复习 问题1: 毕达哥拉斯是古希腊著名的数学家,有一次有位数学家问他:“尊敬的毕达哥拉斯先生,请告诉我,有多少名学生在你的学校里听你讲课?” 毕达哥拉斯回答说:“我的学生,现在有 在学习数学, 在学习音乐, 沉默无言,此外,还有三名妇女.”算一算:毕达哥拉斯的学生有多少名? 你能解出这道方程吗?把你的解法与其他同学交流一下,看谁的解法好。总结:像上面这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,则可以使解方程中的计算更方便些。解:设毕达哥拉斯的学生有x名,由题意得我的学生,现在有 在学习数学, 在学习音乐, 沉默无言,此外,还有三名妇女 英国伦敦博物馆保存着一部极其珍贵的文物——纸莎草文书。这是古代埃及人用象形文字写在一种特殊的草上的著作,它于公元前1700年左右写成,至今已有三千七百多年。这部书中记载了许多有关数学的问题,其中有如下一道著名的求未知数的问题。问题2:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,求这个数?纸莎草文书你能解决这个问题吗?问题 一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33。用现在的数学符号表示,这道题就是方程
解:设这个数为x,像左面这样的方程中
有些系数是分数,
如果能化去分母,
把系数化为整数,
则可以使解方程中
的计算更方便些。各分母的最小公倍数时42,方程两边同乘42,则得到合并同类项,系数化为1,思考:方程两边同乘42的依据是什么?
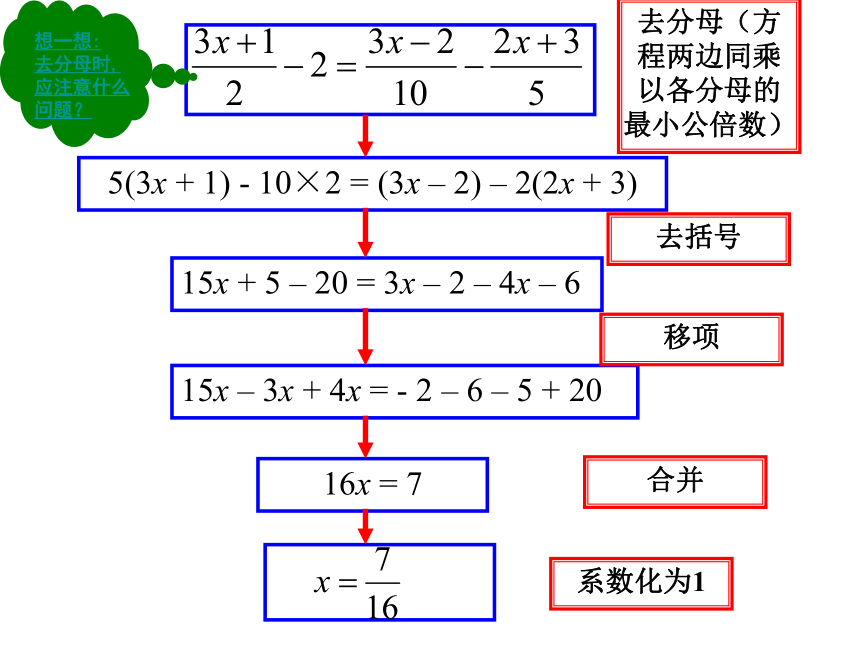
用上述方法解下列方程:(1)这个方程中各分母的最小公倍数是多少?
(2)你认为方程两边应该同时乘以多少?
(3)方程两边同乘上这个数以后分别变成了什么?去分母(方程两边同乘以各分母的最小公倍数)去括号移项合并系数化为1例1 解方程:解:去分母(方程两边同乘6),得18x+3(x-1)=18-2(2x-1).去括号,得18x+3x-3=18-4x+2移项,得18x+3x+4x=18+2+3.合并同类项,得25x=23系数化为1,得? 请你判断 ? 解: 去分母,得 5x-1=8x+4-2(x-1)
去括号,得 5x-1=8x+4-2x-2
移项,得 8x+5x+2x=4-2+1
合并,得 15x =3
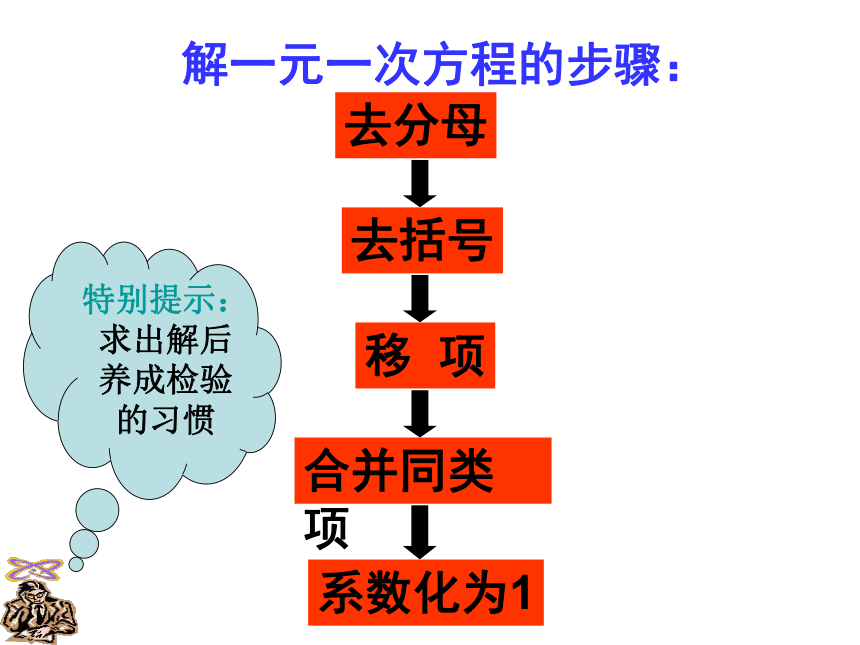
系数化为1,得 x =5 仔细观察 看老师做得对不对? 请你判断 ? 解一元一次方程的步骤:移 项合并同类项系数化为1去括号特别提示:求出解后养成检验的习惯去分母解一元一次方程的一般步骤:2(2x+1)=1-5(x-2)2(2x+1)=1-5(x-2)解:去括号,得 4x+2=1-5x+10移项,得 4x+5x=1+10-2合并,得 9x=9系数化1,得 x=1 例:某工厂要锻造直径为60mm,高为20mm 的圆柱形毛坯,需要截取直径为40mm的圆钢多长? 例:某工厂要锻造长为40mm,宽为30mm ,高为15mm的长方体毛坯,需要截取直径为40mm的圆钢多长? 例:截取20m直径为40m的圆钢,能锻造底面积为120m2的圆柱形毛坯多么长?例: 把先准备好的铁丝围成一个长方形,有多少种围法? 它们的周长改变了吗?它们的面积都相等吗?例:如图所示,小明将一个正方形纸片剪去一个宽为4厘米的长条后,在从剩下的长方形纸片上剪去一个宽为5厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长
条的面积为多少?类型三:打折销售 1、 进 价(成本)
2、 原 价(定价)
3、 售 价
4、 利润
5、利润率
6、折扣一、此类型中的量二、此类型中的等量关系一家商店将某种服装按成本价提高40%后标价,又以8折优惠卖出,结果每件服装仍获利15元.这种
服装每件的成本价是多少元? 一家商店将某种服装按成本价提高40%后标价,
又以8折优惠卖出,结果每件服装仍获利15元.这种
服装每件的成本价是多少元?解: 如果设每件服装的成本价为x元,那么每件服装的标价为:(1+40%)X 元每件服装的实际售价为:80%(1+40%) X 元每件服装的利润为:80%(1+40%)X - X 元由此,列出方程:80%(1+40%)X-X=15解方程,得x=125因此每件服装的成本价是125元。例:某种商品因换季准备打折出售,如
果按定价的七五折出售将赔25元,而
按定价的九折出售将赚20元,这种商
品的定价是多少元?例:张、王、李三户分别装有相同的电灯2
只、4只和3只,共用一块电表,按照电灯
只数分摊16.2元的电费,则各家应分别分摊
多少元电费?例:某洗衣机厂今年计划生产洗衣机3000台,其中Ⅰ型、Ⅱ型、Ⅲ型三种洗衣机的数量的比是2:3:5,这三种洗衣机计划各生产多少台?题型:例:(劳力分配问题)某工程队每天安排
120个劳力修建水库,平均每天每个劳力能
挖土5方或运土3方,为了挖出的土及时运走,
问应如何安排挖土和运土的劳力?例: (比例问题)我国四大发明之一的黑
火药,它所用的原料为硝酸钾、硫磺、木炭,
它们的重量比是15:2:3,要配制这种火药
280千克,三种原料应各取多少千克? 1、某水利工地派 48 人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?练一练 1、某水利工地派 48 人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?练一练解:设安排 x 人去挖土,则有(48 – x )人运土,根据题意,得 5 x = 3 ( 48 – x )
去括号,得 5x = 144 –3x
移项及合并,得 8x = 144
x = 18
运土的人数为 48 – x = 48 –18 = 30
答:应安排18人去挖土,30人去运土,正好能使挖出的土及时运走。3、 某车间每天能生产甲种零件120个,
或乙种零件180个,甲、乙两种零件分别取
2个、3个才能配成一套,现要在30天内生产
最多的成套产品,问怎样安排生产甲、乙
两种零件的天数? 小明在静水中划船的速度为每小时12千米,
今往返于某河,逆流时用了10小时,
顺流时用了6小时.求两地距离。思考题 小明在静水中划船的速度为每小时12千米,
今往返于某河,逆流时用了10小时,
顺流时用了6小时.求两地距离。开放与创新:诗仙李白本性嗜酒、豪放、旷达,向有“斗酒诗百篇”的美誉,是唐代“饮中八仙”之一,民间流传李白买酒歌谣,是一道有趣的数学问题:李白街上走,提壶去买酒;遇店加一倍,见花喝一斗;三遇店和花,喝完壶中酒;试问酒壶中,原有多少酒? 分析:若设酒壶中原有x斗酒,
则李白饮酒的历程可用表格表示为类型五:能追上小明吗?一、涉及到的量 二、三个基本量之间的关系三、类似行程问题的工程问题(路程 速度 时间) 1、路程=速度×时间
2、速度=路程÷时间
3、时间=路程÷速度
1、工作总量 = 工作效率 × 工作时间
2、工作效率 = 工作总量 ÷ 工作时间
3、工作时间 = 工作总量 ÷ 工作效率例:市实验中学学生步行到郊外旅行。(1)班学生组成前队,步行速度为4千米/时,(2)班学生组成后队,速度为6千米/时。前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米时。
根据上面的事实提出问题,并尝试解答。1、后队追上前队需要多长时间?2、后队追上前队时间内,联络员走的路程是多少?3、两队何时相距6千米?4、两队何时相距2千米?例:小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相
向起跑,那么几秒后两人相遇?(2)如果他们两家相距500米,同时出
发多长时间见面? 例:甲、乙两人在一环城公路上骑自行车,环行公路长42km,甲乙两人的速度分别是21km/h,14km/h.
(1)、如果两人从公路的同一地点同时 反向出发,那 么经过几小时后,两人首次相遇?
(2)、如果两人从公路的同一地点 同时同向出发,那么经过几小时后, 两人首次相遇?注水问题:例:一个水池,有甲、乙、丙三个水管,甲、
乙是入水管,丙是排水管,单开甲管16分钟
可将水池注满,单开乙管10分钟可将水池注
满,单开丙管20分钟可将全池水放完。现将
甲、乙两水管打开,4分钟后关上甲管开丙管,
问又经过几分钟才能将水池注满?2、甲工作量+乙工作量+丙工作量=1类型六:教育储蓄一、涉及量二、量之间的关系1、本息和=本金+利息
2、利息税=利息×20℅
3、利息=本金×利率×期数
4、利息=
本金×利率×期数×(1-20℅) 1、本金
2、利息
3、本息和
4、利率
(年、月)
5、期数
6、利息税例:为了准备小敏6年后上大学的学费5000元,她的父母现在就参加了教育储蓄.
下面有两种储蓄方式:
(1)直接存一个6年期;
(2)先存一个3年期的,3
年后将本息和自动转存
一个3年期.你认为哪种储蓄方式开始存入的本金比较少?2.252.702.88 为了准备小颖6年后上大学的费用5000元,她的父
母现在就参加了教育储蓄。下面有两种储蓄方式:
(1)直接存入一个6年期;
(2)先存一个3年期的,3年后将本息和自动转存一
个3年期。
你认为那种储蓄方式开始存入的本金少?设开始存入x元,列出方程:(1+2.88%×6)x=5000元解得 x=4263.3元如果按照第二种储蓄方式,那么1.081×(1+2.7%×3)= 50001.168561x = 5000X≈42791.张先生到银行存了2000元,存期为2年,已知年
利率为2.25%,则两年后,扣除20%的利息税之后
所得的本息和是多少?利息是2000×2.25%×2=90元利息税是90×20%=18元本息和=2000+90-18=2072元【随堂练习】 3、用白铁皮做罐头盒,每张铁片可制盒身10个或制盒底30个。一个盒身与两个盒底配成一套罐头盒。现有100张白铁皮,用多少张制盒身,多少张制盒底,可以既使做出的盒身和盒底配套,又能充分利用白铁皮?盒身的个数×2=盒底的个数
有些系数是分数,
如果能化去分母,
把系数化为整数,
则可以使解方程中
的计算更方便些。各分母的最小公倍数时42,方程两边同乘42,则得到合并同类项,系数化为1,思考:方程两边同乘42的依据是什么?
用上述方法解下列方程:(1)这个方程中各分母的最小公倍数是多少?
(2)你认为方程两边应该同时乘以多少?
(3)方程两边同乘上这个数以后分别变成了什么?去分母(方程两边同乘以各分母的最小公倍数)去括号移项合并系数化为1例1 解方程:解:去分母(方程两边同乘6),得18x+3(x-1)=18-2(2x-1).去括号,得18x+3x-3=18-4x+2移项,得18x+3x+4x=18+2+3.合并同类项,得25x=23系数化为1,得? 请你判断 ? 解: 去分母,得 5x-1=8x+4-2(x-1)
去括号,得 5x-1=8x+4-2x-2
移项,得 8x+5x+2x=4-2+1
合并,得 15x =3
系数化为1,得 x =5 仔细观察 看老师做得对不对? 请你判断 ? 解一元一次方程的步骤:移 项合并同类项系数化为1去括号特别提示:求出解后养成检验的习惯去分母解一元一次方程的一般步骤:2(2x+1)=1-5(x-2)2(2x+1)=1-5(x-2)解:去括号,得 4x+2=1-5x+10移项,得 4x+5x=1+10-2合并,得 9x=9系数化1,得 x=1 例:某工厂要锻造直径为60mm,高为20mm 的圆柱形毛坯,需要截取直径为40mm的圆钢多长? 例:某工厂要锻造长为40mm,宽为30mm ,高为15mm的长方体毛坯,需要截取直径为40mm的圆钢多长? 例:截取20m直径为40m的圆钢,能锻造底面积为120m2的圆柱形毛坯多么长?例: 把先准备好的铁丝围成一个长方形,有多少种围法? 它们的周长改变了吗?它们的面积都相等吗?例:如图所示,小明将一个正方形纸片剪去一个宽为4厘米的长条后,在从剩下的长方形纸片上剪去一个宽为5厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长
条的面积为多少?类型三:打折销售 1、 进 价(成本)
2、 原 价(定价)
3、 售 价
4、 利润
5、利润率
6、折扣一、此类型中的量二、此类型中的等量关系一家商店将某种服装按成本价提高40%后标价,又以8折优惠卖出,结果每件服装仍获利15元.这种
服装每件的成本价是多少元? 一家商店将某种服装按成本价提高40%后标价,
又以8折优惠卖出,结果每件服装仍获利15元.这种
服装每件的成本价是多少元?解: 如果设每件服装的成本价为x元,那么每件服装的标价为:(1+40%)X 元每件服装的实际售价为:80%(1+40%) X 元每件服装的利润为:80%(1+40%)X - X 元由此,列出方程:80%(1+40%)X-X=15解方程,得x=125因此每件服装的成本价是125元。例:某种商品因换季准备打折出售,如
果按定价的七五折出售将赔25元,而
按定价的九折出售将赚20元,这种商
品的定价是多少元?例:张、王、李三户分别装有相同的电灯2
只、4只和3只,共用一块电表,按照电灯
只数分摊16.2元的电费,则各家应分别分摊
多少元电费?例:某洗衣机厂今年计划生产洗衣机3000台,其中Ⅰ型、Ⅱ型、Ⅲ型三种洗衣机的数量的比是2:3:5,这三种洗衣机计划各生产多少台?题型:例:(劳力分配问题)某工程队每天安排
120个劳力修建水库,平均每天每个劳力能
挖土5方或运土3方,为了挖出的土及时运走,
问应如何安排挖土和运土的劳力?例: (比例问题)我国四大发明之一的黑
火药,它所用的原料为硝酸钾、硫磺、木炭,
它们的重量比是15:2:3,要配制这种火药
280千克,三种原料应各取多少千克? 1、某水利工地派 48 人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?练一练 1、某水利工地派 48 人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?练一练解:设安排 x 人去挖土,则有(48 – x )人运土,根据题意,得 5 x = 3 ( 48 – x )
去括号,得 5x = 144 –3x
移项及合并,得 8x = 144
x = 18
运土的人数为 48 – x = 48 –18 = 30
答:应安排18人去挖土,30人去运土,正好能使挖出的土及时运走。3、 某车间每天能生产甲种零件120个,
或乙种零件180个,甲、乙两种零件分别取
2个、3个才能配成一套,现要在30天内生产
最多的成套产品,问怎样安排生产甲、乙
两种零件的天数? 小明在静水中划船的速度为每小时12千米,
今往返于某河,逆流时用了10小时,
顺流时用了6小时.求两地距离。思考题 小明在静水中划船的速度为每小时12千米,
今往返于某河,逆流时用了10小时,
顺流时用了6小时.求两地距离。开放与创新:诗仙李白本性嗜酒、豪放、旷达,向有“斗酒诗百篇”的美誉,是唐代“饮中八仙”之一,民间流传李白买酒歌谣,是一道有趣的数学问题:李白街上走,提壶去买酒;遇店加一倍,见花喝一斗;三遇店和花,喝完壶中酒;试问酒壶中,原有多少酒? 分析:若设酒壶中原有x斗酒,
则李白饮酒的历程可用表格表示为类型五:能追上小明吗?一、涉及到的量 二、三个基本量之间的关系三、类似行程问题的工程问题(路程 速度 时间) 1、路程=速度×时间
2、速度=路程÷时间
3、时间=路程÷速度
1、工作总量 = 工作效率 × 工作时间
2、工作效率 = 工作总量 ÷ 工作时间
3、工作时间 = 工作总量 ÷ 工作效率例:市实验中学学生步行到郊外旅行。(1)班学生组成前队,步行速度为4千米/时,(2)班学生组成后队,速度为6千米/时。前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米时。
根据上面的事实提出问题,并尝试解答。1、后队追上前队需要多长时间?2、后队追上前队时间内,联络员走的路程是多少?3、两队何时相距6千米?4、两队何时相距2千米?例:小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相
向起跑,那么几秒后两人相遇?(2)如果他们两家相距500米,同时出
发多长时间见面? 例:甲、乙两人在一环城公路上骑自行车,环行公路长42km,甲乙两人的速度分别是21km/h,14km/h.
(1)、如果两人从公路的同一地点同时 反向出发,那 么经过几小时后,两人首次相遇?
(2)、如果两人从公路的同一地点 同时同向出发,那么经过几小时后, 两人首次相遇?注水问题:例:一个水池,有甲、乙、丙三个水管,甲、
乙是入水管,丙是排水管,单开甲管16分钟
可将水池注满,单开乙管10分钟可将水池注
满,单开丙管20分钟可将全池水放完。现将
甲、乙两水管打开,4分钟后关上甲管开丙管,
问又经过几分钟才能将水池注满?2、甲工作量+乙工作量+丙工作量=1类型六:教育储蓄一、涉及量二、量之间的关系1、本息和=本金+利息
2、利息税=利息×20℅
3、利息=本金×利率×期数
4、利息=
本金×利率×期数×(1-20℅) 1、本金
2、利息
3、本息和
4、利率
(年、月)
5、期数
6、利息税例:为了准备小敏6年后上大学的学费5000元,她的父母现在就参加了教育储蓄.
下面有两种储蓄方式:
(1)直接存一个6年期;
(2)先存一个3年期的,3
年后将本息和自动转存
一个3年期.你认为哪种储蓄方式开始存入的本金比较少?2.252.702.88 为了准备小颖6年后上大学的费用5000元,她的父
母现在就参加了教育储蓄。下面有两种储蓄方式:
(1)直接存入一个6年期;
(2)先存一个3年期的,3年后将本息和自动转存一
个3年期。
你认为那种储蓄方式开始存入的本金少?设开始存入x元,列出方程:(1+2.88%×6)x=5000元解得 x=4263.3元如果按照第二种储蓄方式,那么1.081×(1+2.7%×3)= 50001.168561x = 5000X≈42791.张先生到银行存了2000元,存期为2年,已知年
利率为2.25%,则两年后,扣除20%的利息税之后
所得的本息和是多少?利息是2000×2.25%×2=90元利息税是90×20%=18元本息和=2000+90-18=2072元【随堂练习】 3、用白铁皮做罐头盒,每张铁片可制盒身10个或制盒底30个。一个盒身与两个盒底配成一套罐头盒。现有100张白铁皮,用多少张制盒身,多少张制盒底,可以既使做出的盒身和盒底配套,又能充分利用白铁皮?盒身的个数×2=盒底的个数
