鲁教版(五四制)八年级数学下册6.3正方形的判定与性质同步练习题(word版含答案)
文档属性
| 名称 | 鲁教版(五四制)八年级数学下册6.3正方形的判定与性质同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 133.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 07:22:02 | ||
图片预览




文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的判定与性质》同步练习题(附答案)
1.如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A.4 B.8 C.16 D.无法计算
2.如图,在正方形ABCD的外侧作等边三角形CDE,则∠AED为( )
A.10° B.15° C.30° D.120°
3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使 ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
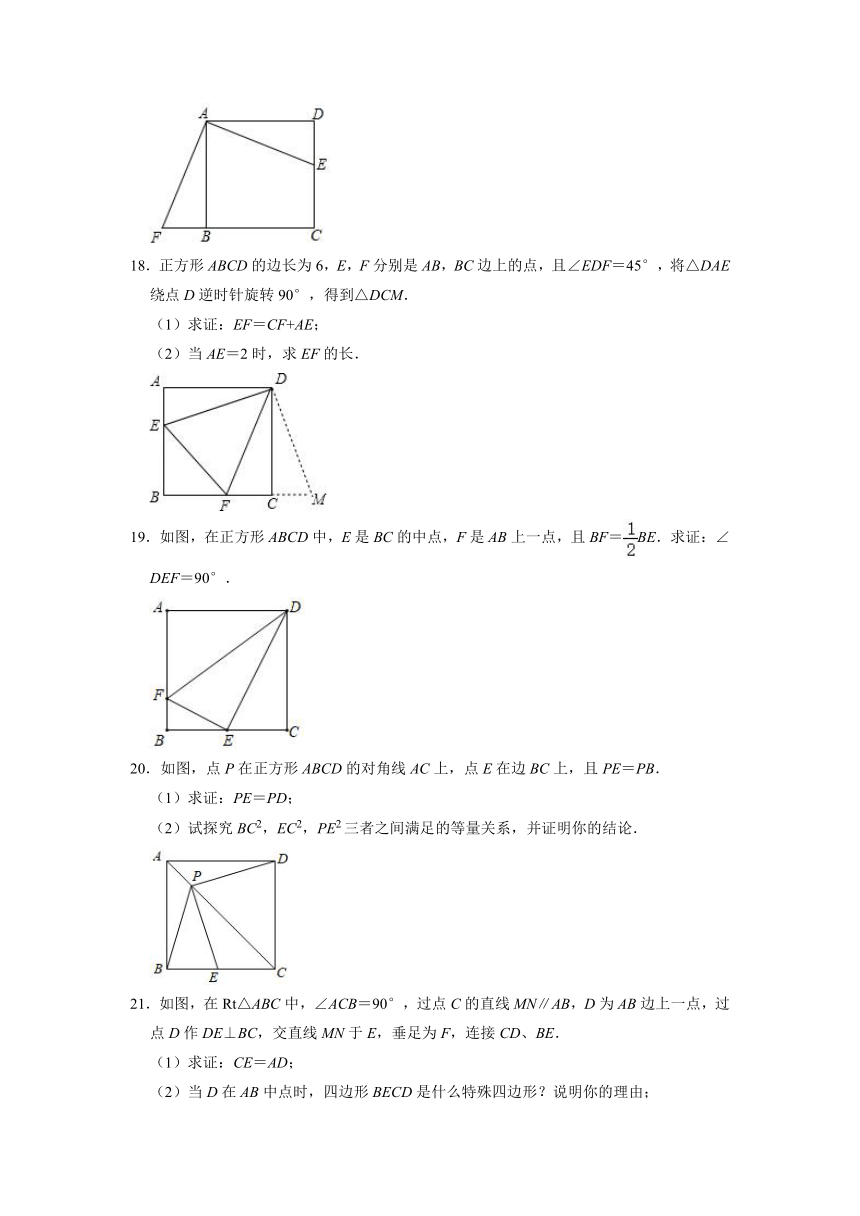
4.如图,在平面直角坐标系中,正方形OABC的顶点O、B的坐标分别是(0,0),(2,0),则顶点C的坐标是( )
A.(1,1) B.(﹣1,﹣1) C.(1,﹣1) D.(﹣1,1)
5.正方形面积为36,则对角线的长为( )
A.6 B. C.9 D.
6.如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
A.64 B.72 C.76 D.84
7.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
8.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.35° B.45° C.55° D.60°
9.如图,在正方形ABCD的外侧作等边△ADE,则∠AEB的度数为( )
A.10° B.12.5° C.15° D.20°
10.如图,已知正方形ABCD的边长为4,M点为CD边上的中点,若M点是A点关于线段EF的对称点,则等于( )
A. B. C.2 D.
11.正方形具有而菱形不具有的性质是( )
A.四条边都相等 B.对角线相等
C.对角线平分一组对角 D.对角线垂直且互相平分
12.下列性质中,矩形具有、正方形也具有、但是菱形却不具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线长度相等 D.一组对角线平分一组对角
13.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
14.如图,在边长为4的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,则EF的最小值为( )
A. B. C.2 D.1
15.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,则∠AEB的度数为 .
16.如图,已知正方形ABCD的边长为6,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=2,则FM的长为 .
17.如图,点E是正方形ABCD的边DC上一点,点F是CB延长线上一点,且△ADE≌△ABF,四边形AECF的面积为8,DE=1,则AE的长为 .
18.正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
19.如图,在正方形ABCD中,E是BC的中点,F是AB上一点,且BF=BE.求证:∠DEF=90°.
20.如图,点P在正方形ABCD的对角线AC上,点E在边BC上,且PE=PB.
(1)求证:PE=PD;
(2)试探究BC2,EC2,PE2三者之间满足的等量关系,并证明你的结论.
21.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
参考答案
1.解:∵四边形ABCD是正方形,
∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE,
∴S四边形AFCE=S正方形ABCD=16.
故选:C.
2.解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
∵△CDE是等边三角形,
∴DE=DC,∠EDC=60°,
∴∠ADE=90°+60°=150°,AD=ED,
∴∠DAE=∠DEA=(180°﹣∠ADE)=15°,
故选:B.
3.解:A、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;
B、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;
C、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意;
D、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.
故选:B.
4.解:连接AC,
∵四边形OABC是正方形,
∴点A、C关于x轴对称,
∴AC所在直线为OB的垂直平分线,即A、C的横坐标均为1,
根据正方形对角线相等的性质,AC=BO=2,
又∵A、C关于x轴对称,
∴A点纵坐标为1,C点纵坐标为﹣1,
故C点坐标(1,﹣1),
故选:C.
5.解:设对角线长是x.则有
x2=36,
解得:x=6.
故选:B.
6.解:∵AE垂直于BE,且AE=6,BE=8,
∴在Rt△ABE中,AB2=AE2+BE2=100,
∴S阴影部分=S正方形ABCD﹣S△ABE
=AB2﹣×AE×BE
=100﹣×6×8
=76.
故选:C.
7.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
8.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE=AB,
∴AE=AB=AD,
∴∠ABE=∠AEB,∠AED=∠ADE,∠ABE+∠AEB+∠BAE=180°,∠AED+∠ADE+∠DAE=180°,
∵∠BAE+∠DAE=∠BAD=90°,
∴∠ABE+∠AEB+∠AED+∠ADE=270°,
∴∠AEB+∠AED=135°,
即∠BED=135°,
∴∠BEF=180°﹣135°=45°.
故选:B.
9.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
又∵△ADE是正三角形,
∴AE=AD,∠DAE=60°,
∴△ABE是等腰三角形,∠BAE=90°+60°=150°,
∴∠ABE=∠AEB=15°.
故选:C.
10.解:
连接EM,
∵M、A关于EB对称,
∴EA=EM,设AE=x,
则ED=4﹣x,EM=x
而DM=2,
在直角△DEM中,
由勾股定理得:(4﹣x)2+22=x2
解得:x=
∴4﹣x=
∴=,
故选:A.
11.解:正方形和菱形都满足:四条边都相等,对角线平分一组对角,对角线垂直且互相平分;
菱形的对角线不一定相等,而正方形的对角线一定相等.
故选:B.
12.解:∵菱形具有的性质是:两组对边分别平行,对角线互相平分,对角线互相垂直;
矩形具有的性质是:两组对边分别平行,对角线互相平分,对角线相等;
正方形具有菱形和矩形的性质,
∴菱形不具有的性质为:对角线相等,
故选:C.
13.解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH==,
∴四边形EFGH的面积是:×=34,
故选:B.
14.解:连接MC,如图所示:
∵四边形ABCD是正方形,
∴∠C=90°,∠DBC=45°,
∵ME⊥BC于E,MF⊥CD于F
∴四边形MECF为矩形,
∴EF=MC,
当MC⊥BD时,MC取得最小值,
此时△BCM是等腰直角三角形,
∴MC=BC=2,
∴EF的最小值为2;
故选:B.
15.解:根据等边三角形和正方形的性质可知AB=AE,
∴∠BAE=90°+60°=150°,
∴∠AEB=(180°﹣150°)÷2=15°.
故答案为:15°
16.解:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
,
∴△DEF≌△DMF(SAS),
∴EF=MF,
设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
∴FM=5.
故答案为:5.
17.解:∵△ADE≌△ABF,
∴正方形ABCD的面积等于四边形AECF的面积,
∵四边形AECF的面积为8,
∴正方形ABCD的面积为8.
∴AD2=8,
在Rt△ADE中,AE===3,
故答案为:3.
18.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF,
∴EF=CF+AE;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
19.证明:∵四边形ABCD为正方形,
∴AB=BC=CD=DA,∠B=∠C=∠D=90°.
∵E是BC的中点,且BF=BE,
∴设BF=x,则BE=2x,AB=CD=DA=BC=4x,AF=3x,
在Rt△BFE中,由勾股定理可得EF2=BF2+BE2=5x2,
同理可得:DF2=25x2,DE=20x2,
∴EF2+DE2=DF2,
∴△DEF为直角三角形,
∴∠DEF=90°.
20.(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)解:BC2+EC2=2PE2,证明如下:
连接DE,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD,
由(1)得:△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
∴∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴DE2=PE2+PD2=2PE2,
在Rt△CDE中,由勾股定理得:CD2+EC2=DE2,
∴BC2+EC2=2PE2.
21.(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD(直角三角形斜边上的中线等于斜边的一半),
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
1.如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A.4 B.8 C.16 D.无法计算
2.如图,在正方形ABCD的外侧作等边三角形CDE,则∠AED为( )
A.10° B.15° C.30° D.120°
3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使 ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
4.如图,在平面直角坐标系中,正方形OABC的顶点O、B的坐标分别是(0,0),(2,0),则顶点C的坐标是( )
A.(1,1) B.(﹣1,﹣1) C.(1,﹣1) D.(﹣1,1)
5.正方形面积为36,则对角线的长为( )
A.6 B. C.9 D.
6.如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
A.64 B.72 C.76 D.84
7.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
8.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.35° B.45° C.55° D.60°
9.如图,在正方形ABCD的外侧作等边△ADE,则∠AEB的度数为( )
A.10° B.12.5° C.15° D.20°
10.如图,已知正方形ABCD的边长为4,M点为CD边上的中点,若M点是A点关于线段EF的对称点,则等于( )
A. B. C.2 D.
11.正方形具有而菱形不具有的性质是( )
A.四条边都相等 B.对角线相等
C.对角线平分一组对角 D.对角线垂直且互相平分
12.下列性质中,矩形具有、正方形也具有、但是菱形却不具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线长度相等 D.一组对角线平分一组对角
13.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
14.如图,在边长为4的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,则EF的最小值为( )
A. B. C.2 D.1
15.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,则∠AEB的度数为 .
16.如图,已知正方形ABCD的边长为6,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=2,则FM的长为 .
17.如图,点E是正方形ABCD的边DC上一点,点F是CB延长线上一点,且△ADE≌△ABF,四边形AECF的面积为8,DE=1,则AE的长为 .
18.正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
19.如图,在正方形ABCD中,E是BC的中点,F是AB上一点,且BF=BE.求证:∠DEF=90°.
20.如图,点P在正方形ABCD的对角线AC上,点E在边BC上,且PE=PB.
(1)求证:PE=PD;
(2)试探究BC2,EC2,PE2三者之间满足的等量关系,并证明你的结论.
21.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
参考答案
1.解:∵四边形ABCD是正方形,
∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE,
∴S四边形AFCE=S正方形ABCD=16.
故选:C.
2.解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
∵△CDE是等边三角形,
∴DE=DC,∠EDC=60°,
∴∠ADE=90°+60°=150°,AD=ED,
∴∠DAE=∠DEA=(180°﹣∠ADE)=15°,
故选:B.
3.解:A、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;
B、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;
C、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意;
D、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.
故选:B.
4.解:连接AC,
∵四边形OABC是正方形,
∴点A、C关于x轴对称,
∴AC所在直线为OB的垂直平分线,即A、C的横坐标均为1,
根据正方形对角线相等的性质,AC=BO=2,
又∵A、C关于x轴对称,
∴A点纵坐标为1,C点纵坐标为﹣1,
故C点坐标(1,﹣1),
故选:C.
5.解:设对角线长是x.则有
x2=36,
解得:x=6.
故选:B.
6.解:∵AE垂直于BE,且AE=6,BE=8,
∴在Rt△ABE中,AB2=AE2+BE2=100,
∴S阴影部分=S正方形ABCD﹣S△ABE
=AB2﹣×AE×BE
=100﹣×6×8
=76.
故选:C.
7.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
8.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE=AB,
∴AE=AB=AD,
∴∠ABE=∠AEB,∠AED=∠ADE,∠ABE+∠AEB+∠BAE=180°,∠AED+∠ADE+∠DAE=180°,
∵∠BAE+∠DAE=∠BAD=90°,
∴∠ABE+∠AEB+∠AED+∠ADE=270°,
∴∠AEB+∠AED=135°,
即∠BED=135°,
∴∠BEF=180°﹣135°=45°.
故选:B.
9.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
又∵△ADE是正三角形,
∴AE=AD,∠DAE=60°,
∴△ABE是等腰三角形,∠BAE=90°+60°=150°,
∴∠ABE=∠AEB=15°.
故选:C.
10.解:
连接EM,
∵M、A关于EB对称,
∴EA=EM,设AE=x,
则ED=4﹣x,EM=x
而DM=2,
在直角△DEM中,
由勾股定理得:(4﹣x)2+22=x2
解得:x=
∴4﹣x=
∴=,
故选:A.
11.解:正方形和菱形都满足:四条边都相等,对角线平分一组对角,对角线垂直且互相平分;
菱形的对角线不一定相等,而正方形的对角线一定相等.
故选:B.
12.解:∵菱形具有的性质是:两组对边分别平行,对角线互相平分,对角线互相垂直;
矩形具有的性质是:两组对边分别平行,对角线互相平分,对角线相等;
正方形具有菱形和矩形的性质,
∴菱形不具有的性质为:对角线相等,
故选:C.
13.解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH==,
∴四边形EFGH的面积是:×=34,
故选:B.
14.解:连接MC,如图所示:
∵四边形ABCD是正方形,
∴∠C=90°,∠DBC=45°,
∵ME⊥BC于E,MF⊥CD于F
∴四边形MECF为矩形,
∴EF=MC,
当MC⊥BD时,MC取得最小值,
此时△BCM是等腰直角三角形,
∴MC=BC=2,
∴EF的最小值为2;
故选:B.
15.解:根据等边三角形和正方形的性质可知AB=AE,
∴∠BAE=90°+60°=150°,
∴∠AEB=(180°﹣150°)÷2=15°.
故答案为:15°
16.解:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
,
∴△DEF≌△DMF(SAS),
∴EF=MF,
设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
∴FM=5.
故答案为:5.
17.解:∵△ADE≌△ABF,
∴正方形ABCD的面积等于四边形AECF的面积,
∵四边形AECF的面积为8,
∴正方形ABCD的面积为8.
∴AD2=8,
在Rt△ADE中,AE===3,
故答案为:3.
18.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF,
∴EF=CF+AE;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
19.证明:∵四边形ABCD为正方形,
∴AB=BC=CD=DA,∠B=∠C=∠D=90°.
∵E是BC的中点,且BF=BE,
∴设BF=x,则BE=2x,AB=CD=DA=BC=4x,AF=3x,
在Rt△BFE中,由勾股定理可得EF2=BF2+BE2=5x2,
同理可得:DF2=25x2,DE=20x2,
∴EF2+DE2=DF2,
∴△DEF为直角三角形,
∴∠DEF=90°.
20.(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)解:BC2+EC2=2PE2,证明如下:
连接DE,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD,
由(1)得:△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
∴∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴DE2=PE2+PD2=2PE2,
在Rt△CDE中,由勾股定理得:CD2+EC2=DE2,
∴BC2+EC2=2PE2.
21.(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD(直角三角形斜边上的中线等于斜边的一半),
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
