冀教版七年级下册第六章6.3二元一次方程组的应用 同步练习(含解析)
文档属性
| 名称 | 冀教版七年级下册第六章6.3二元一次方程组的应用 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 13:31:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
冀教版七年级下册第六章6.3二元一次方程组的应用
一、选择题
为了研究吸烟与肺癌的关系,某肿瘤研究所随机地抽查了人,并进行统计分析结果显示:在吸烟者中患肺癌的比例是,在不吸烟者中患肺癌的比例是,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多人如果设这人中,吸烟者患肺癌的人数为,不吸烟者患肺癌的人数为,根据题意,下面列出的方程组正确的是
A. B.
C. D.
如图,有四个相同的小长方形和两个相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是
A. B. C. D.
九章算术是中国古代的数学专著,下面这道题是九章算术中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出钱,则多了钱;如果每人出钱,则少了钱.问有多少人,物品的价格是多少?”设有人,物品价格为钱,可列方程组为
A. B. C. D.
我国古代算法统宗里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住人,那么有人无房住;如果每一间客房住人,那么就空出一间客房.设该店有客房间、房客人,下列方程组中正确的是
A. B. C. D.
某公司有学徒工和熟练工两个工种的工人,已知一个学徒工每天制造的零件比一个熟练工少个,一个学徒工与两个熟练工每天共可制造个零件,求一个学徒工与一个熟练工每天各能制造多少个零件?设一个学徒工每天能制造个零件,一个熟练工每天能制造个零件,根据题意可列方程组为
A. B.
C. D.
中国古代人民在生产生活中发现了许多数学问题,在九章算术中记载了这样一个问题,大意为:“今有只雀、只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,则衡器两边的总重量相等,如果只雀和只燕的总重量为斤,问雀、燕每只各重多少斤?”如果设每只雀重斤,每只燕重斤,则下列方程组正确的是
A. B.
C. D.
夏季来临,某超市试销、两种型号的风扇,两周内共销售台,销售收入元,型风扇每台元,型风扇每台元,问、两种型号的风扇分别销售了多少台?若设型风扇销售了台,型风扇销售了台,则根据题意列出方程组为
A. B.
C. D.
孙子算经中的一道名题:今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?其意思是:用绳子去量一根木头,绳子还剩余尺,将绳子对折再量木头,木头还剩余尺,问木头长多少尺?设木头为尺,绳子为尺,可列方程组为
A. B. C. D.
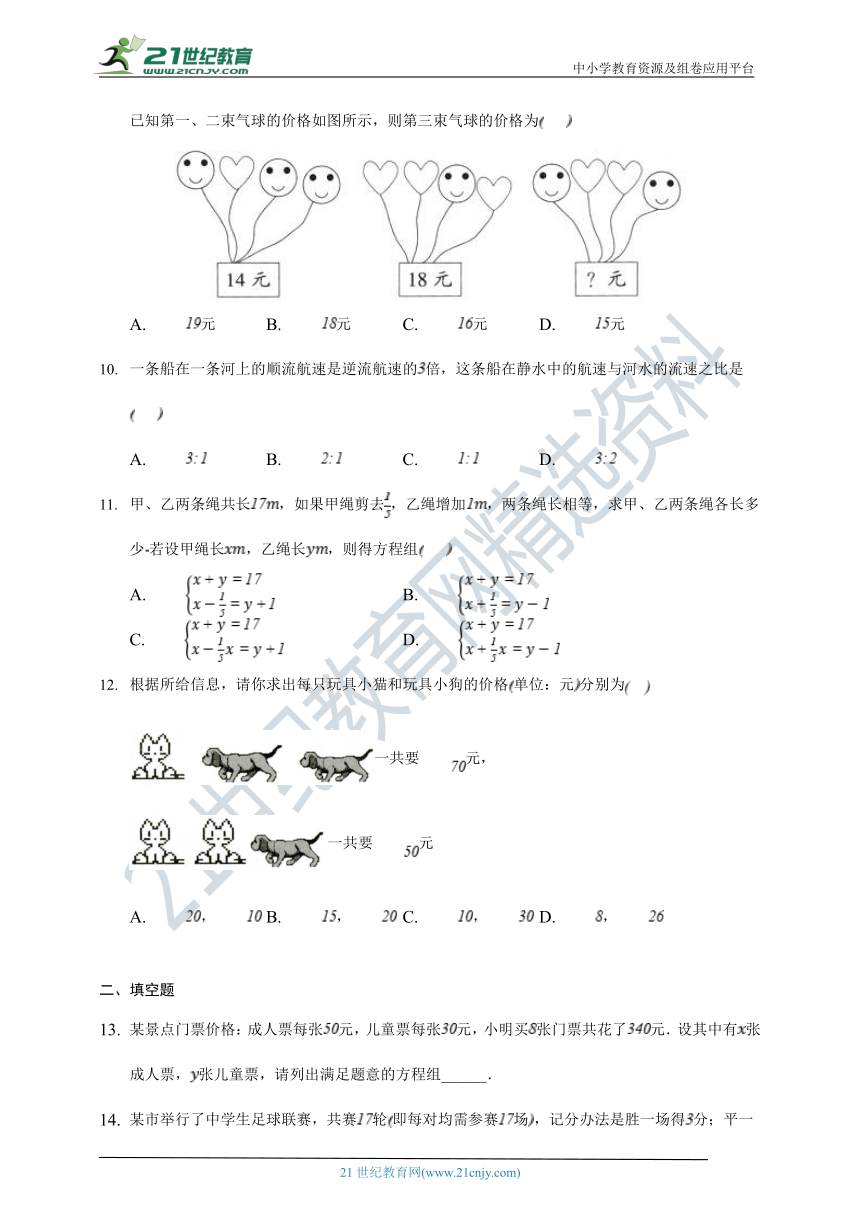
陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束个气球为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为
A. 元 B. 元 C. 元 D. 元
一条船在一条河上的顺流航速是逆流航速的倍,这条船在静水中的航速与河水的流速之比是
A. B. C. D.
甲、乙两条绳共长,如果甲绳剪去,乙绳增加,两条绳长相等,求甲、乙两条绳各长多少若设甲绳长,乙绳长,则得方程组
A. B.
C. D.
根据所给信息,请你求出每只玩具小猫和玩具小狗的价格单位:元分别为
一共要元,
一共要元
A. , B. , C. , D. ,
二、填空题
某景点门票价格:成人票每张元,儿童票每张元,小明买张门票共花了元.设其中有张成人票,张儿童票,请列出满足题意的方程组______.
某市举行了中学生足球联赛,共赛轮即每对均需参赛场,记分办法是胜一场得分;平一场得分,负一场得分.若八中足球积分为分,且踢平场数是所负场数的整数倍,且胜、平、负的场数各不相同.问八中足球队共负______场.
某超市以、两种糖果为原料,组装出了甲、乙、丙三种糖果礼盒礼盒包装成本忽略不计其中,甲礼盒每盒含千克糖果、千克糖果;乙礼盒每盒含千克糖果、千克糖果;丙礼盒每盒含千克糖果、千克糖果.甲礼盒每盒售价元,利润率为国庆节期间,该超市进行打折促销活动,将甲、乙、丙礼盒各一盒合组装成大礼包,并且每购买一个大礼包可免费赠送一个乙礼盒,这样即可实现利润率为,则每个大礼包的售价为______元.
某旅馆的客房有三人间和两人间两种,三人间每人每天元,两人间每人每天元.一个人的旅游团到该旅馆住宿,租住了若干客房,且每个客房正好住满,一天共花去住宿费元.设该旅游团租住三人间客房间,两人间客房间,请列出满足题意的方程组____.
三、解答题
某服装店用元购进,两种新式服装,按标价售出后可获得毛利润元毛利润售价进价,这两种服装的进价、标价如下表所示:
求这两种服装各购进的件数
如果种服装按标价的折出售,种服装按标价的折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元
某山区县的林地面积和耕地面积原来共有,该县响应国家“退耕还林”号召,将一部分耕地恢复为林地后,林地面积增加了,耕地面积减少了设原有耕地面积为,林地面积为,列二元一次方程组.
“利海”通讯器材商场,计划用元从厂家购进若干部新型手机,出厂价分别为甲种型号手机每部元,乙种型号手机每部元,丙种型号手机每部元.若商场同时购进其中两种不同型号的手机共部,并将元恰好用完,请你帮助商场计算一下如何购买.
“端午节”是中国的传统节日,武商超市决定在六月份开展让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买盒甲品牌粽子和盒乙品牌粽子需元;打折后,买盒甲品牌粽子和盒乙品牌粽子需元.
打折前甲、乙两种品牌粽子每盒分别为多少元?
阳光敬老院需购买甲品牌粽子盒,乙品牌粽子盒,问打折后购买这批粽子比不打折节省了多少钱?
答案和解析
1.【答案】
【解析】提示:由“吸烟者患肺癌的人数比不吸烟者患肺癌的人数多人”可列方程为;
由“吸烟者人数不吸烟者人数”及“抽查的不吸烟者人数”可列方程为,
故可列方程组为.
2.【答案】
【解析】解:设小长方形的长为,宽为,
根据题意得:,即,
整理得:.
则小长方形的长与宽的差是.
故选:.
设小长方形的长为,宽为,根据题意由大长方形的长度相等列出方程求出的值,即为长与宽的差.
此题考查了二元一次方程组的应用,解题关键是弄清题意,合适的等量关系,列出方程,注意整体思想的运用.
3.【答案】
【解析】解:由题意可得,
,
故选:.
根据题意可以找出题目中的等量关系,列出相应的方程组,从而可以解答本题.
本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
4.【答案】
【解析】
【试题解析】
【分析】
本题考查了由实际问题抽象出二元一次方程组;根据题意得出方程组是解决问题的关键.
设该店有客房间,房客人;根据题意一房七客多七客,一房九客一房空得出方程组即可.
【解答】
解:设该店有客房间,房客人;
根据题意得:,
故选:.
5.【答案】
【解析】解:根据题意可列方程组为,
故选:.
根据“一个学徒工每天制造的零件比一个熟练工少个,一个学徒工与两个熟练工每天共可制造个零件”可方程组.
本题主要考查由实际问题抽象出二元一次方程组,由实际问题列方程组是把“未知”转化为“已知”的重要方法,它的关键是把已知量和未知量联系起来,找出题目中的相等关系.
6.【答案】
【解析】
【分析】
设每只雀有斤,每只燕有斤,根据五只雀、六只燕,共重斤,雀重燕轻,互换其中一只,恰好一样重,列方程组即可.
本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
【解答】
解:设每只雀有斤,每只燕有斤,
由题意得,,
故选A.
7.【答案】
【解析】
【分析】
本题直接利用两周内共销售台,销售收入元,分别得出等式进而得出答案.
此题主要考查了由实际问题抽象出二元一次方程组,正确得出等量关系是解题关键.
【解答】
解:设型风扇销售了台,型风扇销售了台,
则根据题意列出方程组为:
故选C.
8.【答案】
【解析】解:依题意,得:.
故选:.
根据“用绳子去量一根木头,绳子还剩余尺,将绳子对折再量木头,木头还剩余尺”,即可得出关于,的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
9.【答案】
【解析】提示:设每个笑脸气球的价格为元,每个爱心气球的价格为元,
由题图中信息的等量关系可以列出方程组
解方程组可得
所以每个笑脸气球的价格为元,每个爱心气球的价格为元,
第三束气球的价格为元
10.【答案】
【解析】提示:设船的逆流航速为,河水流速为,则顺流航速为,
那么,
解得,
静水航速顺流航速河水流速,
所以静水航速为,
所以船的静水航速与河水流速之比为.
11.【答案】
【解析】提示:根据甲、乙两条绳共长,得方程;
根据甲绳剪去,乙绳增加,两条绳长相等,得方程,
故列方程组为.
12.【答案】
【解析】
【分析】
本题主要考查了二元一次方程组的应用,解答本题的关键是根据图形列出相关的二元一次方程组.
设一只玩具小猫元,一只玩具小狗元,根据一只小猫和两只小狗一共要元可得,由两只小猫和一只小狗一共要元可得,据此解二元一次方程组,求出,的值即可.
【解答】
解:设一只玩具小猫元,一只玩具小狗元,
根据题意得
解得.
故选C.
13.【答案】
【解析】解:设其中有张成人票,张儿童票,
根据题意得:.
故答案为:.
设其中有张成人票,张儿童票,根据张门票共元,即可得出关于、的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
14.【答案】或
【解析】解:设八中足球队胜了场,平了场,负了场,
由题意得,
,
把代入得:
,
解得:为整数.
又为正整数,
当时,,,,因为胜、平、负的场数各不相同,所以,不符合题意,舍去
当时,,,;
当时,,,,
答:八中足球队负了或场.
故答案为:或.
设该校足球队胜了场,平了场,负了场,依题意建立方程组,解方程组从而用整数表示负场数,根据为整数,分别求出的取值,然后求出、的值,继而可得出该校足球队负几场即可.
本题考查了三元一次组的应用,解答本题的关键是设出未知数列出方程组,用表示出的值,根据为整数,即可分类讨论出的值.
15.【答案】
【解析】解:设原料的成本为元千克,原料的成本为元千克,
根据题意得:,
解得:,
礼盒的售价为元.
故答案为:元.
设原料的成本为元千克,原料的成本为元千克,根据成本利润率售价,即可得出关于,的二元一次方程,解之可得出,的值,找出礼盒及赠品与,之间的关系,再利用售价利润率成本,即可得出结论.
本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
16.【答案】
【解析】
【分析】
本题主要考查由实际问题抽象出二元一次方程组,解答时找到反应全题题意的两个等量关系建立方程组是关键.设租住三人间间,租住两人间间,就可以得出,,由这两个方程构成方程组.
【解答】
解:设租住三人间间,租住两人间间,
由题意,得
故答案为.
17.【答案】解:设种服装购进件,种服装购进件,
由题意得
解得
答:种服装购进件,种服装购进件
由题意,得元.
答:服装店比按标价售出少收入元
18.【答案】解:设原有耕地面积为,林地面积为,由题意得:
.
【解析】根据题意可得等量关系:原有林地面积原有耕地面积,恢复后林地面积恢复后耕地面积,根据等量关系列出方程组即可.
此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系.
19.【答案】解:分三种情况:
设分别购进甲乙两种手机为、部,
依题意得,,
解得:,
即可以购进甲乙两种手机分别是部、部;
设分别购进甲丙两种手机为、部,
依题意得,,
解得:,
即可以购进甲丙两种手机分别是部、部;
设分别购进乙丙两种手机为、部,
依题意得,,
解得:不合题意,舍去,
答:有两种购买方法:甲种型号手机购买部,乙种型号手机购买部;或甲种型号手机购买部,丙种型号手机购买部;
【解析】分三种情况:
设分别购进甲乙两种手机为、部,根据两种不同型号的手机共部,并将元恰好用完可以列出方程组,解方程组即可解决问题;
设分别购进甲丙两种手机为、部,根据两种不同型号的手机共部,并将元恰好用完可以列出方程组,解方程组即可解决问题;
设分别购进乙丙两种手机为、部,根据两种不同型号的手机共部,并将元恰好用完可以列出方程组,解方程组即可解决问题.
本题考查了二元一次方程组的应用,比较复杂,解题的关键是根据已知条件分类讨论,然后在可能的情况下分别列出方程组,解方程组根据解的情况就可以确定购买方案.
20.【答案】解:设打折前甲品牌粽子每盒元,乙品牌粽子每盒元,根据题意得:,
解得:,
答:打折前甲品牌粽子每盒元,乙品牌粽子每盒元;
元,
答:打折后购买这批粽子比不打折节省了元.
【解析】本题考查了二元一次方程组的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;根据数量关系,列式计算.
设打折前甲品牌粽子每盒元,乙品牌粽子每盒元,根据“打折前,买盒甲品牌粽子和盒乙品牌粽子需元;打折后,买盒甲品牌粽子和盒乙品牌粽子需要元”,即可得出关于、的二元一次方程组,解之即可得出结论;
根据节省钱数甲品牌粽子节省的钱数乙品牌粽子节省的钱数,即可求出节省的钱数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
冀教版七年级下册第六章6.3二元一次方程组的应用
一、选择题
为了研究吸烟与肺癌的关系,某肿瘤研究所随机地抽查了人,并进行统计分析结果显示:在吸烟者中患肺癌的比例是,在不吸烟者中患肺癌的比例是,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多人如果设这人中,吸烟者患肺癌的人数为,不吸烟者患肺癌的人数为,根据题意,下面列出的方程组正确的是
A. B.
C. D.
如图,有四个相同的小长方形和两个相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是
A. B. C. D.
九章算术是中国古代的数学专著,下面这道题是九章算术中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出钱,则多了钱;如果每人出钱,则少了钱.问有多少人,物品的价格是多少?”设有人,物品价格为钱,可列方程组为
A. B. C. D.
我国古代算法统宗里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住人,那么有人无房住;如果每一间客房住人,那么就空出一间客房.设该店有客房间、房客人,下列方程组中正确的是
A. B. C. D.
某公司有学徒工和熟练工两个工种的工人,已知一个学徒工每天制造的零件比一个熟练工少个,一个学徒工与两个熟练工每天共可制造个零件,求一个学徒工与一个熟练工每天各能制造多少个零件?设一个学徒工每天能制造个零件,一个熟练工每天能制造个零件,根据题意可列方程组为
A. B.
C. D.
中国古代人民在生产生活中发现了许多数学问题,在九章算术中记载了这样一个问题,大意为:“今有只雀、只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,则衡器两边的总重量相等,如果只雀和只燕的总重量为斤,问雀、燕每只各重多少斤?”如果设每只雀重斤,每只燕重斤,则下列方程组正确的是
A. B.
C. D.
夏季来临,某超市试销、两种型号的风扇,两周内共销售台,销售收入元,型风扇每台元,型风扇每台元,问、两种型号的风扇分别销售了多少台?若设型风扇销售了台,型风扇销售了台,则根据题意列出方程组为
A. B.
C. D.
孙子算经中的一道名题:今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何?其意思是:用绳子去量一根木头,绳子还剩余尺,将绳子对折再量木头,木头还剩余尺,问木头长多少尺?设木头为尺,绳子为尺,可列方程组为
A. B. C. D.
陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束个气球为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为
A. 元 B. 元 C. 元 D. 元
一条船在一条河上的顺流航速是逆流航速的倍,这条船在静水中的航速与河水的流速之比是
A. B. C. D.
甲、乙两条绳共长,如果甲绳剪去,乙绳增加,两条绳长相等,求甲、乙两条绳各长多少若设甲绳长,乙绳长,则得方程组
A. B.
C. D.
根据所给信息,请你求出每只玩具小猫和玩具小狗的价格单位:元分别为
一共要元,
一共要元
A. , B. , C. , D. ,
二、填空题
某景点门票价格:成人票每张元,儿童票每张元,小明买张门票共花了元.设其中有张成人票,张儿童票,请列出满足题意的方程组______.
某市举行了中学生足球联赛,共赛轮即每对均需参赛场,记分办法是胜一场得分;平一场得分,负一场得分.若八中足球积分为分,且踢平场数是所负场数的整数倍,且胜、平、负的场数各不相同.问八中足球队共负______场.
某超市以、两种糖果为原料,组装出了甲、乙、丙三种糖果礼盒礼盒包装成本忽略不计其中,甲礼盒每盒含千克糖果、千克糖果;乙礼盒每盒含千克糖果、千克糖果;丙礼盒每盒含千克糖果、千克糖果.甲礼盒每盒售价元,利润率为国庆节期间,该超市进行打折促销活动,将甲、乙、丙礼盒各一盒合组装成大礼包,并且每购买一个大礼包可免费赠送一个乙礼盒,这样即可实现利润率为,则每个大礼包的售价为______元.
某旅馆的客房有三人间和两人间两种,三人间每人每天元,两人间每人每天元.一个人的旅游团到该旅馆住宿,租住了若干客房,且每个客房正好住满,一天共花去住宿费元.设该旅游团租住三人间客房间,两人间客房间,请列出满足题意的方程组____.
三、解答题
某服装店用元购进,两种新式服装,按标价售出后可获得毛利润元毛利润售价进价,这两种服装的进价、标价如下表所示:
求这两种服装各购进的件数
如果种服装按标价的折出售,种服装按标价的折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元
某山区县的林地面积和耕地面积原来共有,该县响应国家“退耕还林”号召,将一部分耕地恢复为林地后,林地面积增加了,耕地面积减少了设原有耕地面积为,林地面积为,列二元一次方程组.
“利海”通讯器材商场,计划用元从厂家购进若干部新型手机,出厂价分别为甲种型号手机每部元,乙种型号手机每部元,丙种型号手机每部元.若商场同时购进其中两种不同型号的手机共部,并将元恰好用完,请你帮助商场计算一下如何购买.
“端午节”是中国的传统节日,武商超市决定在六月份开展让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买盒甲品牌粽子和盒乙品牌粽子需元;打折后,买盒甲品牌粽子和盒乙品牌粽子需元.
打折前甲、乙两种品牌粽子每盒分别为多少元?
阳光敬老院需购买甲品牌粽子盒,乙品牌粽子盒,问打折后购买这批粽子比不打折节省了多少钱?
答案和解析
1.【答案】
【解析】提示:由“吸烟者患肺癌的人数比不吸烟者患肺癌的人数多人”可列方程为;
由“吸烟者人数不吸烟者人数”及“抽查的不吸烟者人数”可列方程为,
故可列方程组为.
2.【答案】
【解析】解:设小长方形的长为,宽为,
根据题意得:,即,
整理得:.
则小长方形的长与宽的差是.
故选:.
设小长方形的长为,宽为,根据题意由大长方形的长度相等列出方程求出的值,即为长与宽的差.
此题考查了二元一次方程组的应用,解题关键是弄清题意,合适的等量关系,列出方程,注意整体思想的运用.
3.【答案】
【解析】解:由题意可得,
,
故选:.
根据题意可以找出题目中的等量关系,列出相应的方程组,从而可以解答本题.
本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
4.【答案】
【解析】
【试题解析】
【分析】
本题考查了由实际问题抽象出二元一次方程组;根据题意得出方程组是解决问题的关键.
设该店有客房间,房客人;根据题意一房七客多七客,一房九客一房空得出方程组即可.
【解答】
解:设该店有客房间,房客人;
根据题意得:,
故选:.
5.【答案】
【解析】解:根据题意可列方程组为,
故选:.
根据“一个学徒工每天制造的零件比一个熟练工少个,一个学徒工与两个熟练工每天共可制造个零件”可方程组.
本题主要考查由实际问题抽象出二元一次方程组,由实际问题列方程组是把“未知”转化为“已知”的重要方法,它的关键是把已知量和未知量联系起来,找出题目中的相等关系.
6.【答案】
【解析】
【分析】
设每只雀有斤,每只燕有斤,根据五只雀、六只燕,共重斤,雀重燕轻,互换其中一只,恰好一样重,列方程组即可.
本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
【解答】
解:设每只雀有斤,每只燕有斤,
由题意得,,
故选A.
7.【答案】
【解析】
【分析】
本题直接利用两周内共销售台,销售收入元,分别得出等式进而得出答案.
此题主要考查了由实际问题抽象出二元一次方程组,正确得出等量关系是解题关键.
【解答】
解:设型风扇销售了台,型风扇销售了台,
则根据题意列出方程组为:
故选C.
8.【答案】
【解析】解:依题意,得:.
故选:.
根据“用绳子去量一根木头,绳子还剩余尺,将绳子对折再量木头,木头还剩余尺”,即可得出关于,的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
9.【答案】
【解析】提示:设每个笑脸气球的价格为元,每个爱心气球的价格为元,
由题图中信息的等量关系可以列出方程组
解方程组可得
所以每个笑脸气球的价格为元,每个爱心气球的价格为元,
第三束气球的价格为元
10.【答案】
【解析】提示:设船的逆流航速为,河水流速为,则顺流航速为,
那么,
解得,
静水航速顺流航速河水流速,
所以静水航速为,
所以船的静水航速与河水流速之比为.
11.【答案】
【解析】提示:根据甲、乙两条绳共长,得方程;
根据甲绳剪去,乙绳增加,两条绳长相等,得方程,
故列方程组为.
12.【答案】
【解析】
【分析】
本题主要考查了二元一次方程组的应用,解答本题的关键是根据图形列出相关的二元一次方程组.
设一只玩具小猫元,一只玩具小狗元,根据一只小猫和两只小狗一共要元可得,由两只小猫和一只小狗一共要元可得,据此解二元一次方程组,求出,的值即可.
【解答】
解:设一只玩具小猫元,一只玩具小狗元,
根据题意得
解得.
故选C.
13.【答案】
【解析】解:设其中有张成人票,张儿童票,
根据题意得:.
故答案为:.
设其中有张成人票,张儿童票,根据张门票共元,即可得出关于、的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
14.【答案】或
【解析】解:设八中足球队胜了场,平了场,负了场,
由题意得,
,
把代入得:
,
解得:为整数.
又为正整数,
当时,,,,因为胜、平、负的场数各不相同,所以,不符合题意,舍去
当时,,,;
当时,,,,
答:八中足球队负了或场.
故答案为:或.
设该校足球队胜了场,平了场,负了场,依题意建立方程组,解方程组从而用整数表示负场数,根据为整数,分别求出的取值,然后求出、的值,继而可得出该校足球队负几场即可.
本题考查了三元一次组的应用,解答本题的关键是设出未知数列出方程组,用表示出的值,根据为整数,即可分类讨论出的值.
15.【答案】
【解析】解:设原料的成本为元千克,原料的成本为元千克,
根据题意得:,
解得:,
礼盒的售价为元.
故答案为:元.
设原料的成本为元千克,原料的成本为元千克,根据成本利润率售价,即可得出关于,的二元一次方程,解之可得出,的值,找出礼盒及赠品与,之间的关系,再利用售价利润率成本,即可得出结论.
本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
16.【答案】
【解析】
【分析】
本题主要考查由实际问题抽象出二元一次方程组,解答时找到反应全题题意的两个等量关系建立方程组是关键.设租住三人间间,租住两人间间,就可以得出,,由这两个方程构成方程组.
【解答】
解:设租住三人间间,租住两人间间,
由题意,得
故答案为.
17.【答案】解:设种服装购进件,种服装购进件,
由题意得
解得
答:种服装购进件,种服装购进件
由题意,得元.
答:服装店比按标价售出少收入元
18.【答案】解:设原有耕地面积为,林地面积为,由题意得:
.
【解析】根据题意可得等量关系:原有林地面积原有耕地面积,恢复后林地面积恢复后耕地面积,根据等量关系列出方程组即可.
此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系.
19.【答案】解:分三种情况:
设分别购进甲乙两种手机为、部,
依题意得,,
解得:,
即可以购进甲乙两种手机分别是部、部;
设分别购进甲丙两种手机为、部,
依题意得,,
解得:,
即可以购进甲丙两种手机分别是部、部;
设分别购进乙丙两种手机为、部,
依题意得,,
解得:不合题意,舍去,
答:有两种购买方法:甲种型号手机购买部,乙种型号手机购买部;或甲种型号手机购买部,丙种型号手机购买部;
【解析】分三种情况:
设分别购进甲乙两种手机为、部,根据两种不同型号的手机共部,并将元恰好用完可以列出方程组,解方程组即可解决问题;
设分别购进甲丙两种手机为、部,根据两种不同型号的手机共部,并将元恰好用完可以列出方程组,解方程组即可解决问题;
设分别购进乙丙两种手机为、部,根据两种不同型号的手机共部,并将元恰好用完可以列出方程组,解方程组即可解决问题.
本题考查了二元一次方程组的应用,比较复杂,解题的关键是根据已知条件分类讨论,然后在可能的情况下分别列出方程组,解方程组根据解的情况就可以确定购买方案.
20.【答案】解:设打折前甲品牌粽子每盒元,乙品牌粽子每盒元,根据题意得:,
解得:,
答:打折前甲品牌粽子每盒元,乙品牌粽子每盒元;
元,
答:打折后购买这批粽子比不打折节省了元.
【解析】本题考查了二元一次方程组的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;根据数量关系,列式计算.
设打折前甲品牌粽子每盒元,乙品牌粽子每盒元,根据“打折前,买盒甲品牌粽子和盒乙品牌粽子需元;打折后,买盒甲品牌粽子和盒乙品牌粽子需要元”,即可得出关于、的二元一次方程组,解之即可得出结论;
根据节省钱数甲品牌粽子节省的钱数乙品牌粽子节省的钱数,即可求出节省的钱数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
