人教版八年级数学 下册 第十七章 17.2 勾股定理的逆定理 同步练习题(含答案)
文档属性
| 名称 | 人教版八年级数学 下册 第十七章 17.2 勾股定理的逆定理 同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 11:34:19 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十七章 勾股定理
17.2 勾股定理的逆定理
一、选择题
1.满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1∶2∶1 B.三边之比为1∶2∶
C.三边之比为∶2∶ D. 三个内角比为1∶2∶3
2.在△ABC中,∠A,∠B,∠C的对边分别是 a,b,c,那么下面不能判定△ABC是直角三角形的是( )
A.∠B=∠C-∠A
B.a2 = (b+c) (b-c)
C.∠A:∠B:∠C=5 :4 :3
D.a : b : c=5 : 4 : 3
3.已知四个三角形分别满足下列条件:①三角形的三边之比为1:1:;②三角形的三边分别是9、40、41;③三角形三内角之比为1:2:3;④三角形一边上的中线等于这边的一半。其中直角三角形有( )个。
A.4 B.3 C.2 D.1
4.下列命题中是假命题的是( ).
A.△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形.
B.△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形.
C.△ABC中,若∠A∶∠B∶∠C=3∶4∶5则△ABC是直角三角形.
D.△ABC中,若a∶b∶c=5∶4∶3则△ABC是直角三角形.
5.如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
填空题
6.若△ABC的三个外角的度数之比为3:4:5,最大边AB与最小边BC的关系是_________.
7.三边为9、12、15的三角形,其面积为 .
8.如图,D为△ABC的边BC上一点,已知 AB = 13,AD = 12,AC =15,BD=5,则BC的长为 .
9.如图,AB=5,AC=3,BC边上的中线AD=2,且AD⊥AC,则△ABC的面积为______.
10.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_______.
三、解答题
11.已知△ABC的三边长分别是a,b,c,其中a=3,c=5,且关于x的一元二次方程x2-4x+b=0有两个相等的实数根,判断△ABC的形状。
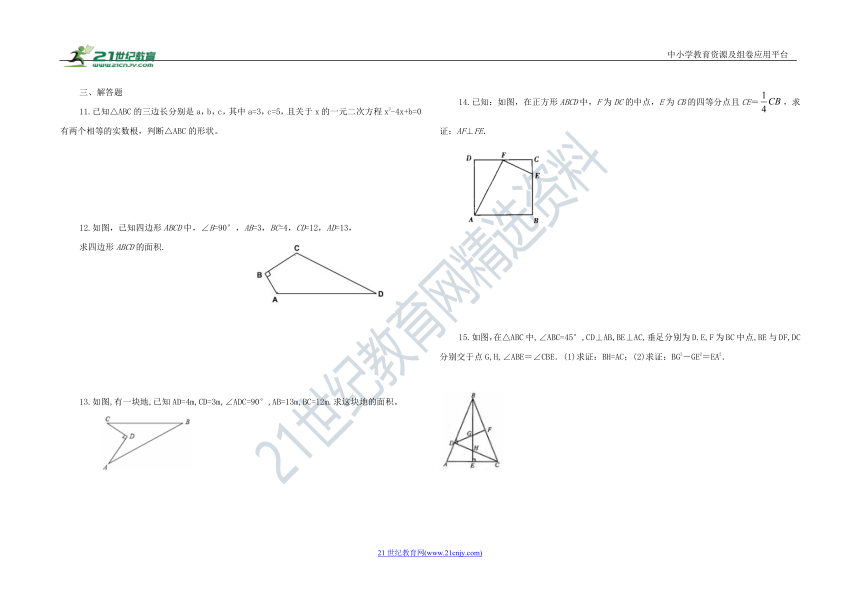
12.如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,
求四边形ABCD的面积.
13.如图,有一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.求这块地的面积。
14.已知:如图,在正方形ABCD中,F为DC的中点,E为CB的四等分点且CE=,求证:AF⊥FE.
15.如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D.E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.(1)求证:BH=AC;(2)求证:BG2-GE2=EA2.
16.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的
C处有一筐水果,一只猴子从D处上爬到树顶A处,
利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处
滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,
求树高AB.
17.观察下列各组勾股数的组成特点,你能求出第7组勾股数a,b,c各是多少吗?第n组呢?
第 1 组:3=2X1+1,4=2X1X(1+1),5=2X1X(1 + 1)+1;
第 2 组:5=2X2+1,12=2X2X(2+1),13=2X2X(2+1) + 1;
第 3 组:7=2X3+1,24=2X3X(3+1),25=2X3X(3+1) + 1;
第 4 组:9=2X4+1,40=2X4X(4+1),41=2X4X(4+1) + 1;
…;
第 7 组:a,b,c.
18.如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?
参考答案:
一、1.C 2.C 3.A 4.C 5.A
二、6.AB=2BC
7.54,提示:先根基勾股定理逆定理得三角形是直角三角形,面积为
8. 14 解析 由AD2+BD2=AB2可知ΔABC为直角三角形,则AD为ΔABC的BC边上的高,在RtΔACD中,CD2=AC2-AD2=152-122=81,所以CD=9,BC=BD+CD=5+9=14.
9.6.提示:延长AD到E,使DE=AD,连结BE,可得△ABE为Rt△.
10.4
三、11.【答案】∵关于x的一元二次方程x2-4x+b=0有两个相等的实数根,
∴b2-4ac=16-4b=0
解得:b=4,
∵a=3,c=5,
∴32+42=52,
∴△ABC为直角三角形.
12.解:连接AC,在Rt△ABC中,
AC2=AB2+BC2=32+42=25, ∴ AC=5.
在△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
∴ AC2+CD2=AB2,∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD=AB·BC+AC·CD=×3×4+×5×12=6+30=36.
13.解:连接AC,∵∠ADC=90°,AD=4,CD=3,∴AC2=AD2+CD2=42+32=25,∴AC=5.又∵BC=12,AB=13,∴AC2+BC2=52+122=169,又∵AB2=169,∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°,∴S四边形ABCD=S△ABC-S△ADC=×12×5-×3×4=24m2.
14.提示:连结AE,设正方形的边长为4a,计算得出AF,EF,AE的长,由AF2+EF2=AE2得结论.
15.证明:(1)∵CD⊥AB,BE⊥AC,∴∠BDH=∠BEC=∠CDA=90°,∵∠ABC=45°,∴∠BCD=180°-90°-45°=45°=∠ABC∴DB=DC.∵∠BDH=∠BEC=∠CDA=90°,∴∠A+∠ACD=90°,∠A+∠HBD=90°,∴∠HBD=∠ACD. ∵在△DBH和△DCA中, ∠BDH=∠CDA, BD=CD,∠HBD=∠ACD,∴△DBH≌△DCA(ASA),∴BH=AC.
(2)连接CG,由(1)知DB=CD.∵F为BC的中点,∴DF垂直平分BC,∴BG=CG.∵点E为AC中点,BE⊥AC,∴EC=EA.在Rt△CGE中,由勾股定理得CG2-GE2=CE2.∵CE=AE,BG=CG,∴BG2-GE2=EA2.
16.设AD=x米,则AB为(10+x)米,AC为(15-x)米,BC为5米,∴(x+10)2+52=(15-x)2,解得x=2,∴10+x=12(米)
17.分析:观察已知勾股数的特点,找出规律.
解:第7组:a=2×7+1=15,b=2×7×(7+1)=112,c=2×7×(7+1)+1=113.
第n组:a=2n+1,b=2n(n+1),c=2n(n+1)+1.
18.【答案】BM=8×2=16海里,
BP=15×2=30海里,
在△BMP中,BM2+BP2=256+900=1156,PM2=1156,
BM2+BP2=PM2,
∴∠MBP=90°,
180°-90°-60°=30°,
故乙船沿南偏东30°方向航行。
21世纪教育网(www.21cnjy.com)
第十七章 勾股定理
17.2 勾股定理的逆定理
一、选择题
1.满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1∶2∶1 B.三边之比为1∶2∶
C.三边之比为∶2∶ D. 三个内角比为1∶2∶3
2.在△ABC中,∠A,∠B,∠C的对边分别是 a,b,c,那么下面不能判定△ABC是直角三角形的是( )
A.∠B=∠C-∠A
B.a2 = (b+c) (b-c)
C.∠A:∠B:∠C=5 :4 :3
D.a : b : c=5 : 4 : 3
3.已知四个三角形分别满足下列条件:①三角形的三边之比为1:1:;②三角形的三边分别是9、40、41;③三角形三内角之比为1:2:3;④三角形一边上的中线等于这边的一半。其中直角三角形有( )个。
A.4 B.3 C.2 D.1
4.下列命题中是假命题的是( ).
A.△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形.
B.△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形.
C.△ABC中,若∠A∶∠B∶∠C=3∶4∶5则△ABC是直角三角形.
D.△ABC中,若a∶b∶c=5∶4∶3则△ABC是直角三角形.
5.如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
填空题
6.若△ABC的三个外角的度数之比为3:4:5,最大边AB与最小边BC的关系是_________.
7.三边为9、12、15的三角形,其面积为 .
8.如图,D为△ABC的边BC上一点,已知 AB = 13,AD = 12,AC =15,BD=5,则BC的长为 .
9.如图,AB=5,AC=3,BC边上的中线AD=2,且AD⊥AC,则△ABC的面积为______.
10.在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_______.
三、解答题
11.已知△ABC的三边长分别是a,b,c,其中a=3,c=5,且关于x的一元二次方程x2-4x+b=0有两个相等的实数根,判断△ABC的形状。
12.如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,
求四边形ABCD的面积.
13.如图,有一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.求这块地的面积。
14.已知:如图,在正方形ABCD中,F为DC的中点,E为CB的四等分点且CE=,求证:AF⊥FE.
15.如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D.E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.(1)求证:BH=AC;(2)求证:BG2-GE2=EA2.
16.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的
C处有一筐水果,一只猴子从D处上爬到树顶A处,
利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处
滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,
求树高AB.
17.观察下列各组勾股数的组成特点,你能求出第7组勾股数a,b,c各是多少吗?第n组呢?
第 1 组:3=2X1+1,4=2X1X(1+1),5=2X1X(1 + 1)+1;
第 2 组:5=2X2+1,12=2X2X(2+1),13=2X2X(2+1) + 1;
第 3 组:7=2X3+1,24=2X3X(3+1),25=2X3X(3+1) + 1;
第 4 组:9=2X4+1,40=2X4X(4+1),41=2X4X(4+1) + 1;
…;
第 7 组:a,b,c.
18.如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?
参考答案:
一、1.C 2.C 3.A 4.C 5.A
二、6.AB=2BC
7.54,提示:先根基勾股定理逆定理得三角形是直角三角形,面积为
8. 14 解析 由AD2+BD2=AB2可知ΔABC为直角三角形,则AD为ΔABC的BC边上的高,在RtΔACD中,CD2=AC2-AD2=152-122=81,所以CD=9,BC=BD+CD=5+9=14.
9.6.提示:延长AD到E,使DE=AD,连结BE,可得△ABE为Rt△.
10.4
三、11.【答案】∵关于x的一元二次方程x2-4x+b=0有两个相等的实数根,
∴b2-4ac=16-4b=0
解得:b=4,
∵a=3,c=5,
∴32+42=52,
∴△ABC为直角三角形.
12.解:连接AC,在Rt△ABC中,
AC2=AB2+BC2=32+42=25, ∴ AC=5.
在△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
∴ AC2+CD2=AB2,∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD=AB·BC+AC·CD=×3×4+×5×12=6+30=36.
13.解:连接AC,∵∠ADC=90°,AD=4,CD=3,∴AC2=AD2+CD2=42+32=25,∴AC=5.又∵BC=12,AB=13,∴AC2+BC2=52+122=169,又∵AB2=169,∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°,∴S四边形ABCD=S△ABC-S△ADC=×12×5-×3×4=24m2.
14.提示:连结AE,设正方形的边长为4a,计算得出AF,EF,AE的长,由AF2+EF2=AE2得结论.
15.证明:(1)∵CD⊥AB,BE⊥AC,∴∠BDH=∠BEC=∠CDA=90°,∵∠ABC=45°,∴∠BCD=180°-90°-45°=45°=∠ABC∴DB=DC.∵∠BDH=∠BEC=∠CDA=90°,∴∠A+∠ACD=90°,∠A+∠HBD=90°,∴∠HBD=∠ACD. ∵在△DBH和△DCA中, ∠BDH=∠CDA, BD=CD,∠HBD=∠ACD,∴△DBH≌△DCA(ASA),∴BH=AC.
(2)连接CG,由(1)知DB=CD.∵F为BC的中点,∴DF垂直平分BC,∴BG=CG.∵点E为AC中点,BE⊥AC,∴EC=EA.在Rt△CGE中,由勾股定理得CG2-GE2=CE2.∵CE=AE,BG=CG,∴BG2-GE2=EA2.
16.设AD=x米,则AB为(10+x)米,AC为(15-x)米,BC为5米,∴(x+10)2+52=(15-x)2,解得x=2,∴10+x=12(米)
17.分析:观察已知勾股数的特点,找出规律.
解:第7组:a=2×7+1=15,b=2×7×(7+1)=112,c=2×7×(7+1)+1=113.
第n组:a=2n+1,b=2n(n+1),c=2n(n+1)+1.
18.【答案】BM=8×2=16海里,
BP=15×2=30海里,
在△BMP中,BM2+BP2=256+900=1156,PM2=1156,
BM2+BP2=PM2,
∴∠MBP=90°,
180°-90°-60°=30°,
故乙船沿南偏东30°方向航行。
21世纪教育网(www.21cnjy.com)
