冀教版数学七年级下册第七章7.5平行线的性质 同步练习(含解析)
文档属性
| 名称 | 冀教版数学七年级下册第七章7.5平行线的性质 同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 13:40:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
冀教版数学七年级下册第七章7.5平行线的性质
一、选择题
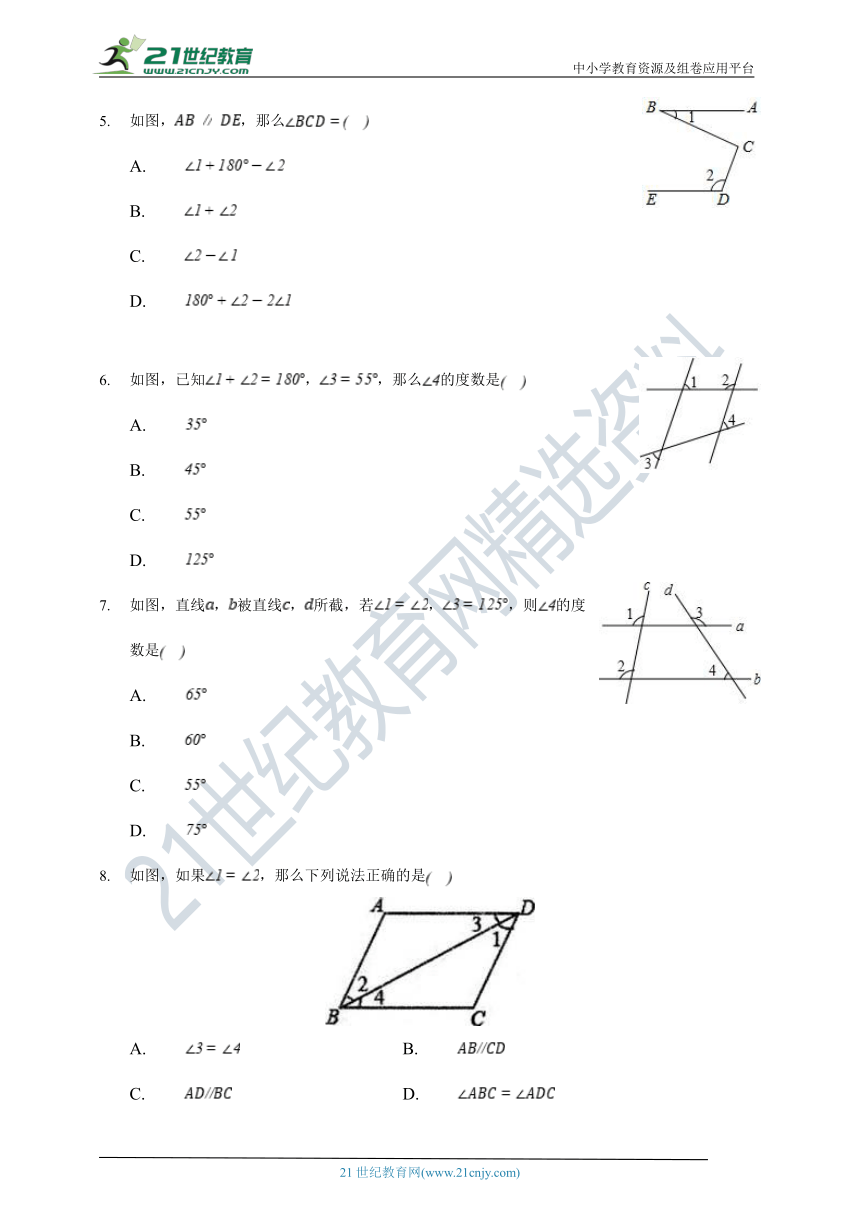
如图,将一张矩形纸片折叠,若,则的度数是
A. B. C. D.
如图,三角板的直角顶点落在长方形纸片的一边上.若,则的度数是
A.
B.
C.
D.
如图,平行线,被直线所截,若,则等于
A.
B.
C.
D.
一个零件的形状如图所示,,,,,则的度数是
A.
B.
C.
D.
如图, ,那么
A.
B.
C.
D.
如图,已知,,那么的度数是
A.
B.
C.
D.
如图,直线,被直线,所截,若,,则的度数是
A.
B.
C.
D.
如图,如果,那么下列说法正确的是
A. B.
C. D.
如图,直线,是直线上的动点,当点的位置变化时,三角形的面积将
A. 变小
B. 变大
C. 不变
D. 变大变小要看点向左还是向右移动
如图,,是的高,过点作,则下列线段的长可表示图中两条平行线之间的距离的是
A.
B.
C.
D.
二、填空题
如图,直线、被直线所截,,,则______.
如图,,,则_________。
如图,若直线 ,,,则的度数为__________.
如图所示,,表示直线与之间距离的是线段______的长度.
三、解答题
如图,直线,与、分别交于点、,且,交直线于点.
若,求的度数;
若,,求直线与的距离.
如图,定义:直线与交于点,对于平面内任意一点,点到直线,的距离分别为,,则称有序实数对是点的“距离坐标”根据上述定义,求“距离坐标”是的点的个数.
如图,在中,于,于,.
求证:.
如图,已知,,垂足分别为、,,试说明:请补充说明过程,并在括号内填上相应的理由.
解:,已知
______,
______,
____________
又已知,
______,
____________,
______
已知;如图,在四边形中,,,的平分线、分别与线段相交于点、,与相交于点,求证:.
答案和解析
1.【答案】
【解析】解:,
,
由翻折不变性可知:,
故选:.
2.【答案】
【解析】解:
,,
,
由题意的纸片的对边平行,
,
故选:.
3.【答案】
【解析】解:如图,平行线,被直线所截,
.
又,
.
故选:.
根据“两直线平行,同旁内角互补”解答.
考查了平行线的性质.平行线性质定理:
定理:两直线平行,同位角相等.
定理:两直线平行,同旁内角互补.
定理:两直线平行,内错角相等.
4.【答案】
【解析】解:,,
,,
,,
,,
,
故选:.
5.【答案】
【解析】解:如图,过点作使,则,
,,
,
即,
故选A.
6.【答案】
【解析】解:如图,
,
,
,
,,
,
故选:.
7.【答案】
【解析】解:,
,
,
,
,
故选:.
8.【答案】
【解析】
解:,
,
故选B.
9.【答案】
【解析】解:设平行线、间的距离为,
则,
长度不变,大小不变,
三角形的面积不变.
故选C.
10.【答案】
【解析】解:表示图中两条平行线之间的距离的是,
故选:.
根据平行线之间的距离的定义解答即可.
本题考查了平行线之间的距离,熟记定义是解题的关键.
11.【答案】
【解析】解:,
,
,
.
故答案为:.
12.【答案】
【解析解:
,
,
,
又,
.
13.【答案】
【解析】解:延长交于,
,
,
,
,
.
14.【答案】
【解析】解:由题可得,,,
直线与直线之间的距离是线段的长度,
故答案为:.
从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,由此可得出答案.
本题考查了平行线之间的距离:从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.
15.【答案】解:直线,
,
又,
,
;
如图,过作于,则的长即为直线与的距离.
,,
,
,
,
直线与的距离为.
16.【答案】解:“距离坐标”是的点表示的含义是该点到直线 , 的距离分别为,.
由于到直线 的距离是的点在与直线 平行且与 的距离是的两条平行线 或 上,
到直线 的距离是的点在与直线 平行且与 的距离是的两条平行线 或 上,它们有个交点,即为如图所示的点 , , , .
故满足条件的点的个数为.
17.【答案】证明:,,
,
,
,
又,
,
,
.
18.【答案】垂直的定义 同位角相等两直线平行 两直线平行同旁内角互补 同角的补角相等 内错角相等两直线平行 两直线平行同位角相等
【解析】解:,已知
垂直的定义,
同位角相等两直线平行,
两直线平行同旁内角互补,
又已知,
同角的补角相等,
内错角相等两直线平行,
两直线平行同位角相等.
故答案为:垂直的定义,同位角相等两直线平行,,两直线平行同旁内角互补,同角的补角相等,,内错角相等两直线平行,两直线平行同位角相等.
根据平行线的判定和性质,垂直的定义,同角的补角相等知识一一判断即可.
本题考查平行线的判定和性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.【答案】证明:,
.
,分别是,的平分线,
,.
.
.
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
冀教版数学七年级下册第七章7.5平行线的性质
一、选择题
如图,将一张矩形纸片折叠,若,则的度数是
A. B. C. D.
如图,三角板的直角顶点落在长方形纸片的一边上.若,则的度数是
A.
B.
C.
D.
如图,平行线,被直线所截,若,则等于
A.
B.
C.
D.
一个零件的形状如图所示,,,,,则的度数是
A.
B.
C.
D.
如图, ,那么
A.
B.
C.
D.
如图,已知,,那么的度数是
A.
B.
C.
D.
如图,直线,被直线,所截,若,,则的度数是
A.
B.
C.
D.
如图,如果,那么下列说法正确的是
A. B.
C. D.
如图,直线,是直线上的动点,当点的位置变化时,三角形的面积将
A. 变小
B. 变大
C. 不变
D. 变大变小要看点向左还是向右移动
如图,,是的高,过点作,则下列线段的长可表示图中两条平行线之间的距离的是
A.
B.
C.
D.
二、填空题
如图,直线、被直线所截,,,则______.
如图,,,则_________。
如图,若直线 ,,,则的度数为__________.
如图所示,,表示直线与之间距离的是线段______的长度.
三、解答题
如图,直线,与、分别交于点、,且,交直线于点.
若,求的度数;
若,,求直线与的距离.
如图,定义:直线与交于点,对于平面内任意一点,点到直线,的距离分别为,,则称有序实数对是点的“距离坐标”根据上述定义,求“距离坐标”是的点的个数.
如图,在中,于,于,.
求证:.
如图,已知,,垂足分别为、,,试说明:请补充说明过程,并在括号内填上相应的理由.
解:,已知
______,
______,
____________
又已知,
______,
____________,
______
已知;如图,在四边形中,,,的平分线、分别与线段相交于点、,与相交于点,求证:.
答案和解析
1.【答案】
【解析】解:,
,
由翻折不变性可知:,
故选:.
2.【答案】
【解析】解:
,,
,
由题意的纸片的对边平行,
,
故选:.
3.【答案】
【解析】解:如图,平行线,被直线所截,
.
又,
.
故选:.
根据“两直线平行,同旁内角互补”解答.
考查了平行线的性质.平行线性质定理:
定理:两直线平行,同位角相等.
定理:两直线平行,同旁内角互补.
定理:两直线平行,内错角相等.
4.【答案】
【解析】解:,,
,,
,,
,,
,
故选:.
5.【答案】
【解析】解:如图,过点作使,则,
,,
,
即,
故选A.
6.【答案】
【解析】解:如图,
,
,
,
,,
,
故选:.
7.【答案】
【解析】解:,
,
,
,
,
故选:.
8.【答案】
【解析】
解:,
,
故选B.
9.【答案】
【解析】解:设平行线、间的距离为,
则,
长度不变,大小不变,
三角形的面积不变.
故选C.
10.【答案】
【解析】解:表示图中两条平行线之间的距离的是,
故选:.
根据平行线之间的距离的定义解答即可.
本题考查了平行线之间的距离,熟记定义是解题的关键.
11.【答案】
【解析】解:,
,
,
.
故答案为:.
12.【答案】
【解析解:
,
,
,
又,
.
13.【答案】
【解析】解:延长交于,
,
,
,
,
.
14.【答案】
【解析】解:由题可得,,,
直线与直线之间的距离是线段的长度,
故答案为:.
从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,由此可得出答案.
本题考查了平行线之间的距离:从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.
15.【答案】解:直线,
,
又,
,
;
如图,过作于,则的长即为直线与的距离.
,,
,
,
,
直线与的距离为.
16.【答案】解:“距离坐标”是的点表示的含义是该点到直线 , 的距离分别为,.
由于到直线 的距离是的点在与直线 平行且与 的距离是的两条平行线 或 上,
到直线 的距离是的点在与直线 平行且与 的距离是的两条平行线 或 上,它们有个交点,即为如图所示的点 , , , .
故满足条件的点的个数为.
17.【答案】证明:,,
,
,
,
又,
,
,
.
18.【答案】垂直的定义 同位角相等两直线平行 两直线平行同旁内角互补 同角的补角相等 内错角相等两直线平行 两直线平行同位角相等
【解析】解:,已知
垂直的定义,
同位角相等两直线平行,
两直线平行同旁内角互补,
又已知,
同角的补角相等,
内错角相等两直线平行,
两直线平行同位角相等.
故答案为:垂直的定义,同位角相等两直线平行,,两直线平行同旁内角互补,同角的补角相等,,内错角相等两直线平行,两直线平行同位角相等.
根据平行线的判定和性质,垂直的定义,同角的补角相等知识一一判断即可.
本题考查平行线的判定和性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.【答案】证明:,
.
,分别是,的平分线,
,.
.
.
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
