人教版八年级数学下册17.2勾股定理的逆定理(寒假衔接预习检测卷) (word版含解析)
文档属性
| 名称 | 人教版八年级数学下册17.2勾股定理的逆定理(寒假衔接预习检测卷) (word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 71.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 09:20:11 | ||
图片预览




文档简介
【寒假衔接】人教版 八年级数学下册
17.2勾股定理的逆定理(预习检测卷)
一、选择题(共8题)
若 ,, 为 的三边长,则下列条件中不能判定 是直角三角形的是
A. ,, B.
C. D.
长度为下列三个数据的三条线段,能组成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
在① ,,;② ,,;③ ,,;④ ,, 这四组数中,勾股数组有
A. 组 B. 组 C. 组 D. 组
下列各组数据中的三个数分别作为三角形的边长,其中能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
已知 ,, 是三角形的三边长,如果满足 ,则三角形的形状是
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
满足下列条件时, 不是直角三角形的为
A. ,, B.
C. D.
已知 , 是线段 上的两点,,,以点 为圆心, 长为半径画弧;再以点 为圆心, 长为半径画弧,两弧交于点 ,连接 ,,则 一定是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
某市地图上有一块草地,三边长分别为 ,,,已知这块草地最短边的实际长度为 ,则这块草地的实际面积是
A. B. C. D.
二、填空题(共7题)
用 根火柴棒首尾顺次连接, (选填“能”或“不能”)组成一个直角三角形.
在 中,若三边 ,, 满足 ,则 是 三角形.
如果三角形的三边长 ,, 满足 ,那么这个三角形是 , .
一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理 .
如果两个命题的题设、结论正好相反,我们就把这样的两个命题叫做 .如果把其中一个叫做原命题,那么另一个叫做它的 .
若一个三角形的三边的比为 ,则这个三角形的三边上的高之比为 .
掌握勾股定理的逆定理
如果三角形的三边长 ,, 满足 ,那么这个三角形是直角三角形.
三、解答题(共5题)
如图,点 ,, 在格点上,若小正方形的边长均为 ,试判断 的形状,并说明理由.
判断由线段 ,, 组成的三角形是不是直角三角形.
(1) ,,;
(2) ,,;
(3) ,,;
(4) ,,( 为正整数).
判断由线段 ,, 组成的三角形是否是直角三角形.
(1) ,,;
(2) ,,;
(3) ,,;
(4) .
已知 中,,,.
(1) 求证: 是直角三角形;
(2) 当 时,求 , 满足的关系式.
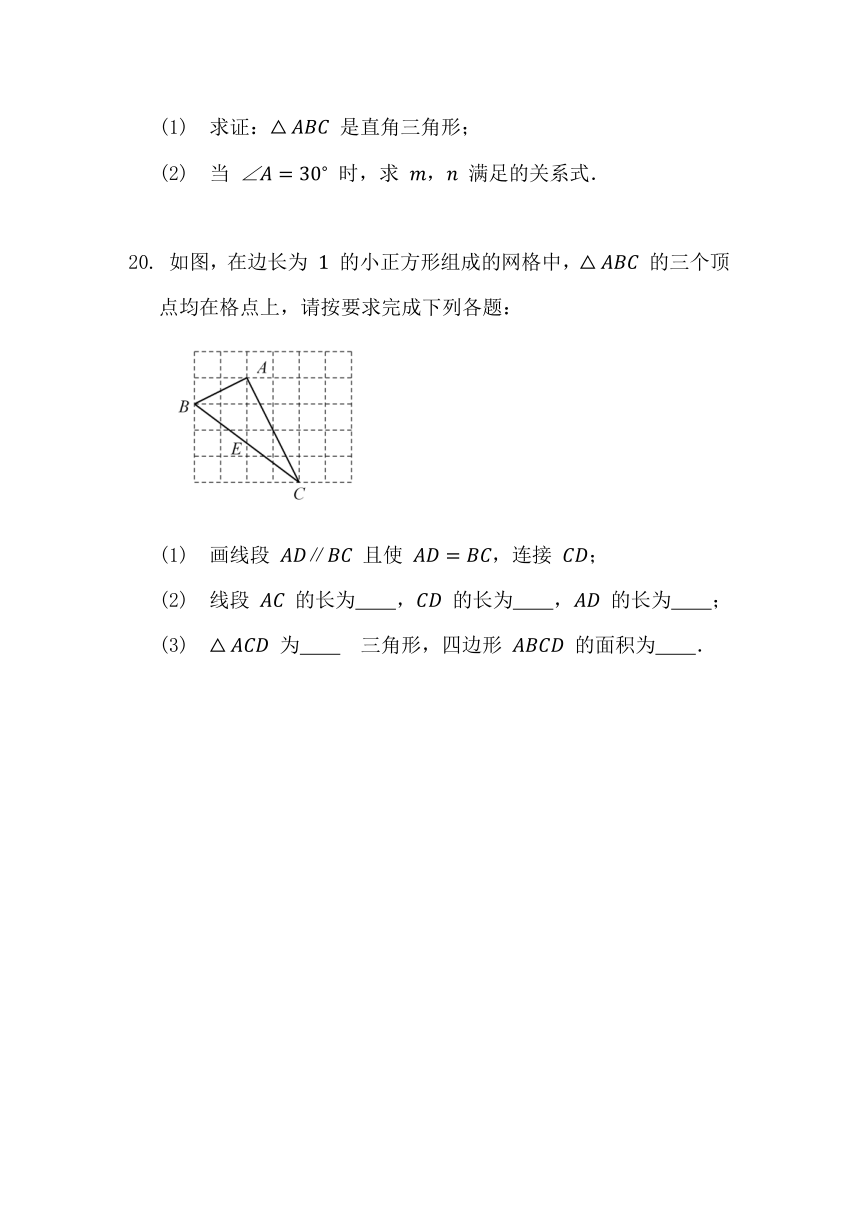
如图,在边长为 的小正方形组成的网格中, 的三个顶点均在格点上,请按要求完成下列各题:
(1) 画线段 且使 ,连接 ;
(2) 线段 的长为 , 的长为 , 的长为 ;
(3) 为 三角形,四边形 的面积为 .
答案
一、选择题(共8题)
1. 【答案】D
【解析】A选项中,,即 ,满足勾股定理,故是直角三角形;
B选项中,, 满足勾股定理,故是直角三角形;
C选项中,,,所以 ,故是直角三角形;
D中,,,则 ,,,故不是直角三角形.
故选D.
【知识点】勾股逆定理
2. 【答案】D
【解析】A.,不能组成直角三角形,故此选项错误;
B.,不能组成直角三角形,故此选项错误;
C.,不能组成直角三角形,故此选项错误;
D.,能组成直角三角形,故此选项正确.
【知识点】勾股逆定理
3. 【答案】B
【知识点】勾股逆定理
4. 【答案】C
【知识点】勾股逆定理
5. 【答案】C
【知识点】勾股逆定理
6. 【答案】C
【知识点】勾股逆定理
7. 【答案】B
【知识点】勾股逆定理
8. 【答案】D
【知识点】勾股逆定理
二、填空题(共7题)
9. 【答案】能
【知识点】勾股逆定理
10. 【答案】直角
【知识点】勾股逆定理
11. 【答案】直角三角形;
【知识点】勾股逆定理
12. 【答案】互为逆定理
13. 【答案】互逆命题;逆命题
【知识点】逆命题
14. 【答案】
【知识点】勾股逆定理
15. 【答案】
【知识点】勾股逆定理
三、解答题(共5题)
16. 【答案】 是直角三角形.
理由:由题意,可知 ,,.
.
是直角三角形.
【知识点】勾股定理、勾股逆定理
17. 【答案】
(1) .不符合勾股定理的逆定理,不是直角三角形;
(2) ,符合勾股定理的逆定理,是直角三角形;
(3) ,符合勾股定理的逆定理,是直角三角形;
(4) ,符合勾股定理的逆定理,是直角三角形.
【知识点】勾股逆定理
18. 【答案】
(1) ,,
.
这个三角形是直角三角形.
(2) ,,
.
这个三角形是直角三角形.
(3) ,,
.
这个三角形不是直角三角形.
(4) 设三角形的三边长分别为 ,,,
,,
.
这个三角形是直角三角形.
【知识点】勾股逆定理、勾股定理
19. 【答案】
(1) ,,,
.
是为直角三角形;
(2) ,
,
.
【知识点】勾股逆定理、30度所对的直角边等于斜边的一半
20. 【答案】
(1) 如图:
(2) ;;
(3) 直角;
【知识点】勾股逆定理、勾股定理、平行线的画法
17.2勾股定理的逆定理(预习检测卷)
一、选择题(共8题)
若 ,, 为 的三边长,则下列条件中不能判定 是直角三角形的是
A. ,, B.
C. D.
长度为下列三个数据的三条线段,能组成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
在① ,,;② ,,;③ ,,;④ ,, 这四组数中,勾股数组有
A. 组 B. 组 C. 组 D. 组
下列各组数据中的三个数分别作为三角形的边长,其中能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
已知 ,, 是三角形的三边长,如果满足 ,则三角形的形状是
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
满足下列条件时, 不是直角三角形的为
A. ,, B.
C. D.
已知 , 是线段 上的两点,,,以点 为圆心, 长为半径画弧;再以点 为圆心, 长为半径画弧,两弧交于点 ,连接 ,,则 一定是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
某市地图上有一块草地,三边长分别为 ,,,已知这块草地最短边的实际长度为 ,则这块草地的实际面积是
A. B. C. D.
二、填空题(共7题)
用 根火柴棒首尾顺次连接, (选填“能”或“不能”)组成一个直角三角形.
在 中,若三边 ,, 满足 ,则 是 三角形.
如果三角形的三边长 ,, 满足 ,那么这个三角形是 , .
一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理 .
如果两个命题的题设、结论正好相反,我们就把这样的两个命题叫做 .如果把其中一个叫做原命题,那么另一个叫做它的 .
若一个三角形的三边的比为 ,则这个三角形的三边上的高之比为 .
掌握勾股定理的逆定理
如果三角形的三边长 ,, 满足 ,那么这个三角形是直角三角形.
三、解答题(共5题)
如图,点 ,, 在格点上,若小正方形的边长均为 ,试判断 的形状,并说明理由.
判断由线段 ,, 组成的三角形是不是直角三角形.
(1) ,,;
(2) ,,;
(3) ,,;
(4) ,,( 为正整数).
判断由线段 ,, 组成的三角形是否是直角三角形.
(1) ,,;
(2) ,,;
(3) ,,;
(4) .
已知 中,,,.
(1) 求证: 是直角三角形;
(2) 当 时,求 , 满足的关系式.
如图,在边长为 的小正方形组成的网格中, 的三个顶点均在格点上,请按要求完成下列各题:
(1) 画线段 且使 ,连接 ;
(2) 线段 的长为 , 的长为 , 的长为 ;
(3) 为 三角形,四边形 的面积为 .
答案
一、选择题(共8题)
1. 【答案】D
【解析】A选项中,,即 ,满足勾股定理,故是直角三角形;
B选项中,, 满足勾股定理,故是直角三角形;
C选项中,,,所以 ,故是直角三角形;
D中,,,则 ,,,故不是直角三角形.
故选D.
【知识点】勾股逆定理
2. 【答案】D
【解析】A.,不能组成直角三角形,故此选项错误;
B.,不能组成直角三角形,故此选项错误;
C.,不能组成直角三角形,故此选项错误;
D.,能组成直角三角形,故此选项正确.
【知识点】勾股逆定理
3. 【答案】B
【知识点】勾股逆定理
4. 【答案】C
【知识点】勾股逆定理
5. 【答案】C
【知识点】勾股逆定理
6. 【答案】C
【知识点】勾股逆定理
7. 【答案】B
【知识点】勾股逆定理
8. 【答案】D
【知识点】勾股逆定理
二、填空题(共7题)
9. 【答案】能
【知识点】勾股逆定理
10. 【答案】直角
【知识点】勾股逆定理
11. 【答案】直角三角形;
【知识点】勾股逆定理
12. 【答案】互为逆定理
13. 【答案】互逆命题;逆命题
【知识点】逆命题
14. 【答案】
【知识点】勾股逆定理
15. 【答案】
【知识点】勾股逆定理
三、解答题(共5题)
16. 【答案】 是直角三角形.
理由:由题意,可知 ,,.
.
是直角三角形.
【知识点】勾股定理、勾股逆定理
17. 【答案】
(1) .不符合勾股定理的逆定理,不是直角三角形;
(2) ,符合勾股定理的逆定理,是直角三角形;
(3) ,符合勾股定理的逆定理,是直角三角形;
(4) ,符合勾股定理的逆定理,是直角三角形.
【知识点】勾股逆定理
18. 【答案】
(1) ,,
.
这个三角形是直角三角形.
(2) ,,
.
这个三角形是直角三角形.
(3) ,,
.
这个三角形不是直角三角形.
(4) 设三角形的三边长分别为 ,,,
,,
.
这个三角形是直角三角形.
【知识点】勾股逆定理、勾股定理
19. 【答案】
(1) ,,,
.
是为直角三角形;
(2) ,
,
.
【知识点】勾股逆定理、30度所对的直角边等于斜边的一半
20. 【答案】
(1) 如图:
(2) ;;
(3) 直角;
【知识点】勾股逆定理、勾股定理、平行线的画法
