北师大版九年级上册2.6 应用一元二次方程 同步练习(word版含答案)
文档属性
| 名称 | 北师大版九年级上册2.6 应用一元二次方程 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 66.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 10:13:47 | ||
图片预览

文档简介
2.6 应用一元二次方程
一、选择题(共10小题;共50分)
1. 在一次同学聚会上,每人都向其他人赠送了一份小礼品,共互送 份小礼品,若设参加聚会的同学有 名,则下列方程正确的是
A. B.
C. D.
2. 若两个相邻自然数的积是 ,则这两个数中,较大的数是
A. B. C. D.
3. 如题图,把一块长为 ,宽为 的矩形便纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒,若该无盖纸盒的底面积为 ,设剪去小正方形的边长为 ,则可列方程为
A. B.
C. D.
4. 某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植 株时,平均每株盈利 元;在此基础上若每盆多植 株,平均每株盈利减少 元,要使每盆的盈利达到 元,每盆应多植多少株 设每盆多植 株,则可以列出的方程是
A. B.
C. D.
5. 游行队伍有 行 列,后又增加了 人,且队伍增加的行、列数相同,设增加的行、列数为 ,下列方程符合题意的是
A.
B.
C.
D.
6. 在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛 场.设有 个队参赛,根据题意,可列方程为
A. B.
C. D.
7. 某市今年从第二季度开始到年底全面实现垃圾分类.已知该市一共有 个社区,第二季度已有 个社区实现垃圾分类,第三、四季度实现垃圾分类的社区个数较前一季度的平均增长率为 ,则下面所列方程正确的是
A.
B.
C.
D.
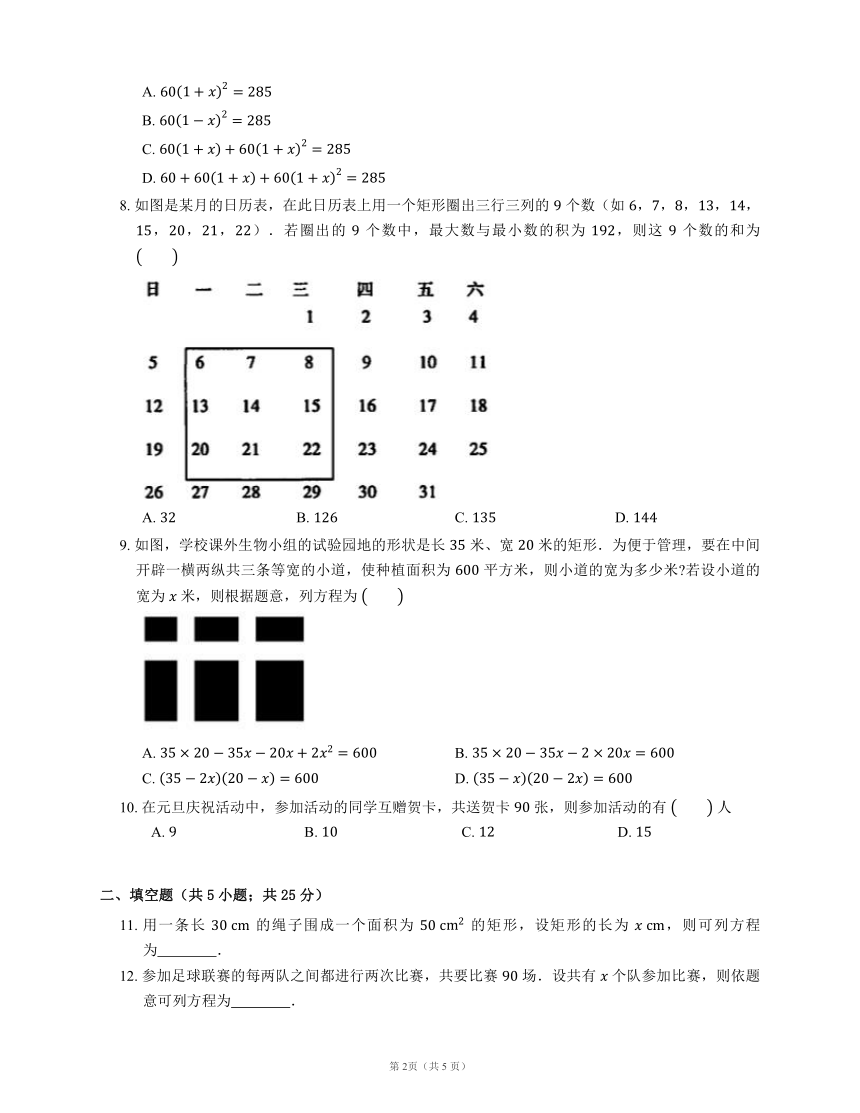
8. 如图是某月的日历表,在此日历表上用一个矩形圈出三行三列的 个数(如 ,,,,,,,,).若圈出的 个数中,最大数与最小数的积为 ,则这 个数的和为
A. B. C. D.
9. 如图,学校课外生物小组的试验园地的形状是长 米、宽 米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为 平方米,则小道的宽为多少米 若设小道的宽为 米,则根据题意,列方程为
A. B.
C. D.
10. 在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡 张,则参加活动的有 人
A. B. C. D.
二、填空题(共5小题;共25分)
11. 用一条长 的绳子围成一个面积为 的矩形,设矩形的长为 ,则可列方程为 .
12. 参加足球联赛的每两队之间都进行两次比赛,共要比赛 场.设共有 个队参加比赛,则依题意可列方程为 .
13. 某小组有若干人,新年大家互相发一条微信祝福,已知全组共发微信 条,则这个小组的人数为 人.
14. 两个连续奇数之积为 ,则这两个奇数分别为 .
15. 某机械厂九月份生产零件 万个,十月份生产零件 万个.设该机械厂九、十月份生产零件数量的月平均增长率为 ,则可列方程为 .
三、解答题(共4小题;共52分)
16. 为倡导“我运动、我健康、我快乐”的生活方式,学校团委准备组织一次篮球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排 天,每天安排 场比赛,学校团委应该邀请多少个队参赛
17. 如图,一块长 米宽 米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的 .
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价 元,其余部分每平方米造价 元,求地毯的总造价.
18. 读诗词解题(通过列方程,算出周瑜去世时的年龄):
大江东去浪淘尽,千古风流数人物.
而立之年( 岁的代称)督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符(相等).
哪位学子算得快,多少年华属周瑜
19. 一商店销售某种商品,平均每天可售出 件,每件盈利 元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于 元的前提下,经过一段时间销售,发现销售单价每降低 元,平均每天可多售出 件.
(1)若销售单价降低 元,则平均每天盈利多少元
(2)当销售单价降低多少元时,该商品每天的盈利为 元
答案
第一部分
1. B
2. B
3. D
4. A 【解析】根据“每盆花卉株数 平均每株盈利 总盈利”得出方程.
5. B
【解析】依题意,得 .
故选B.
6. A
7. D
8. D 【解析】根据题意可以得出,圈出的 个数中,最大数与最小数的差为 ,设最小数为 ,则最大数为 ,所以 ,解得 ,(不合题意,舍去),故圈出的 个数中,第一行的三个数为 ,,,第二行的三个数为 ,,,第三行的三个数为 ,,,故这 个数的和为 .
9. C
10. B
第二部分
11.
12.
13.
14. , 或 ,
15.
第三部分
16. 设学校团委应该邀请 个队参赛.
根据题意,得
整理,得
解得
答:学校团委应该邀请 个队参赛.
17. (1) 设条纹的宽度为 米.依题意得
解得:
答:配色条纹宽度为 米.
(2) 条纹造价:(元),
其余部分造价:(元),
总造价为:(元),
答:地毯的总造价是 元.
18. 设周瑜去世时的年龄的个位数字为 ,则十位数字为 .由题意得
解得
当 时,周瑜的年龄为 岁,不到而立之年,不合题意,舍去;
当 时,周瑜的年龄为 岁,符合题意.
答:周瑜去世时的年龄为 岁.
19. (1) 若销售单价降低 元,则平均每天可多售出 (件),
平均每天盈利 (元).
(2) 设销售单价降低 元时,该商店每天的盈利为 元.
由题意,得
整理,得
解得
每件盈利不少于 元,
.
解得 .
.
答:当销售单价降低 元时,该商品每天的盈利为 元.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 在一次同学聚会上,每人都向其他人赠送了一份小礼品,共互送 份小礼品,若设参加聚会的同学有 名,则下列方程正确的是
A. B.
C. D.
2. 若两个相邻自然数的积是 ,则这两个数中,较大的数是
A. B. C. D.
3. 如题图,把一块长为 ,宽为 的矩形便纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒,若该无盖纸盒的底面积为 ,设剪去小正方形的边长为 ,则可列方程为
A. B.
C. D.
4. 某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植 株时,平均每株盈利 元;在此基础上若每盆多植 株,平均每株盈利减少 元,要使每盆的盈利达到 元,每盆应多植多少株 设每盆多植 株,则可以列出的方程是
A. B.
C. D.
5. 游行队伍有 行 列,后又增加了 人,且队伍增加的行、列数相同,设增加的行、列数为 ,下列方程符合题意的是
A.
B.
C.
D.
6. 在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛 场.设有 个队参赛,根据题意,可列方程为
A. B.
C. D.
7. 某市今年从第二季度开始到年底全面实现垃圾分类.已知该市一共有 个社区,第二季度已有 个社区实现垃圾分类,第三、四季度实现垃圾分类的社区个数较前一季度的平均增长率为 ,则下面所列方程正确的是
A.
B.
C.
D.
8. 如图是某月的日历表,在此日历表上用一个矩形圈出三行三列的 个数(如 ,,,,,,,,).若圈出的 个数中,最大数与最小数的积为 ,则这 个数的和为
A. B. C. D.
9. 如图,学校课外生物小组的试验园地的形状是长 米、宽 米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为 平方米,则小道的宽为多少米 若设小道的宽为 米,则根据题意,列方程为
A. B.
C. D.
10. 在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡 张,则参加活动的有 人
A. B. C. D.
二、填空题(共5小题;共25分)
11. 用一条长 的绳子围成一个面积为 的矩形,设矩形的长为 ,则可列方程为 .
12. 参加足球联赛的每两队之间都进行两次比赛,共要比赛 场.设共有 个队参加比赛,则依题意可列方程为 .
13. 某小组有若干人,新年大家互相发一条微信祝福,已知全组共发微信 条,则这个小组的人数为 人.
14. 两个连续奇数之积为 ,则这两个奇数分别为 .
15. 某机械厂九月份生产零件 万个,十月份生产零件 万个.设该机械厂九、十月份生产零件数量的月平均增长率为 ,则可列方程为 .
三、解答题(共4小题;共52分)
16. 为倡导“我运动、我健康、我快乐”的生活方式,学校团委准备组织一次篮球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排 天,每天安排 场比赛,学校团委应该邀请多少个队参赛
17. 如图,一块长 米宽 米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的 .
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价 元,其余部分每平方米造价 元,求地毯的总造价.
18. 读诗词解题(通过列方程,算出周瑜去世时的年龄):
大江东去浪淘尽,千古风流数人物.
而立之年( 岁的代称)督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符(相等).
哪位学子算得快,多少年华属周瑜
19. 一商店销售某种商品,平均每天可售出 件,每件盈利 元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于 元的前提下,经过一段时间销售,发现销售单价每降低 元,平均每天可多售出 件.
(1)若销售单价降低 元,则平均每天盈利多少元
(2)当销售单价降低多少元时,该商品每天的盈利为 元
答案
第一部分
1. B
2. B
3. D
4. A 【解析】根据“每盆花卉株数 平均每株盈利 总盈利”得出方程.
5. B
【解析】依题意,得 .
故选B.
6. A
7. D
8. D 【解析】根据题意可以得出,圈出的 个数中,最大数与最小数的差为 ,设最小数为 ,则最大数为 ,所以 ,解得 ,(不合题意,舍去),故圈出的 个数中,第一行的三个数为 ,,,第二行的三个数为 ,,,第三行的三个数为 ,,,故这 个数的和为 .
9. C
10. B
第二部分
11.
12.
13.
14. , 或 ,
15.
第三部分
16. 设学校团委应该邀请 个队参赛.
根据题意,得
整理,得
解得
答:学校团委应该邀请 个队参赛.
17. (1) 设条纹的宽度为 米.依题意得
解得:
答:配色条纹宽度为 米.
(2) 条纹造价:(元),
其余部分造价:(元),
总造价为:(元),
答:地毯的总造价是 元.
18. 设周瑜去世时的年龄的个位数字为 ,则十位数字为 .由题意得
解得
当 时,周瑜的年龄为 岁,不到而立之年,不合题意,舍去;
当 时,周瑜的年龄为 岁,符合题意.
答:周瑜去世时的年龄为 岁.
19. (1) 若销售单价降低 元,则平均每天可多售出 (件),
平均每天盈利 (元).
(2) 设销售单价降低 元时,该商店每天的盈利为 元.
由题意,得
整理,得
解得
每件盈利不少于 元,
.
解得 .
.
答:当销售单价降低 元时,该商品每天的盈利为 元.
第1页(共1 页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
