2021-2022学年人教版九年级数学上册第23章旋转寒假自主提升测评 (word版解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册第23章旋转寒假自主提升测评 (word版解析) |  | |
| 格式 | docx | ||
| 文件大小 | 876.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 12:06:46 | ||
图片预览

文档简介
2021-2022学年人教版九年级数学上册《第23章旋转》寒假自主提升测评(附答案)
一、单选题(满分40分)
1.下面四个图案中,是中心对称不是轴对称图形的是( )
A. B. C. D.
2.若点A(n,5)与点B(-1,m)关于原点对称,则( )
A.4 B.-4 C.6 D.- 6
3.如图,在平面直角坐标系中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,其中A、B、C分别和D、E、F对应,则旋转中心的坐标是( )
A.(0,0) B. C. D.
4.如图,在中,,将绕点逆时针旋转得到,使点的对应点恰好落在边上,点的对应点为,延长交于点,则下列结论一定正确的是( )
A. B. C. D.
5.如图,ODC是由OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数是( )
A.30° B.45° C.60° D.75°
6.如图,在△ABC中,∠ACB=45°,BC=1,AC=2,将△ABC绕点A逆时针旋转得到,其中点与点B是对应点,且点C、、在同一条直线上,则的长为( )
A.3 B.4 C.2.5 D.3
7.如图将△ABC绕点C(0,﹣1)旋转180°得到△ABC,设点的坐标为(a,b),则A的坐标为( )
A.(﹣a,﹣b) B.(﹣a,﹣b﹣1) C.(﹣a,﹣b+1) D.(﹣a,﹣b﹣2)
8.如图,ABC是等腰直角三角形,BC是斜边,将ABP绕点A逆时针旋转后得到,如果AP=2,那么的长等于( )
A. B. C. D.
二、填空题(满分40分)
9.在“正三角形,平行四边形,菱形,矩形,正方形”中,是轴对称图形但不是中心对称图形的是 _______.
10.如图, ABC绕点B旋转后到达△BDE处,若∠ABC=120°,∠CBD=30°,则∠DBE=_______,∠CBE=________________.
11.如图,△ABC是边长为2的等边三角形,点D为BC边上的中点,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为____.
12.在平面直角坐标系中,已知点与点关于原点对称.则______.
13.如图,在中,,将绕点按逆时针方向旋转得到.若点恰好落在边上,且,则的度数为______.
14.如图,点M,N分别在正方形ABCD的边BC,CD上,且把绕点A顺时针旋转得到,若正方形的周长为12,,则ME的长为______.
15.如图,在中,,,延长至点P,使,将线段绕点C逆时针旋转角得到,连结,.
(1)当时,点到直线的距离为_________;
(2)当时,点到直线的距离为_________.
16.如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转角(0°<<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角度数为__,△ADF是等腰三角形.
三、解答题(满分40分)
17.如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中,画出一个与△ABC成中心对称的格点三角形;
(2)在图2中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
18.如图,在等边中,点是边上一点,连接将绕点顺时针旋转后得到,连接.
(1)是_ 三角形;
(2)若,求的周长;
(3)求证:.
19.在中,,将绕点C顺时针旋转,得,D,E分别是点B,A的对应点.记旋转角为.
(1)如图①,连接AD,若,,,求AD的长;
(2)如图②,连接BD,若,求证:.
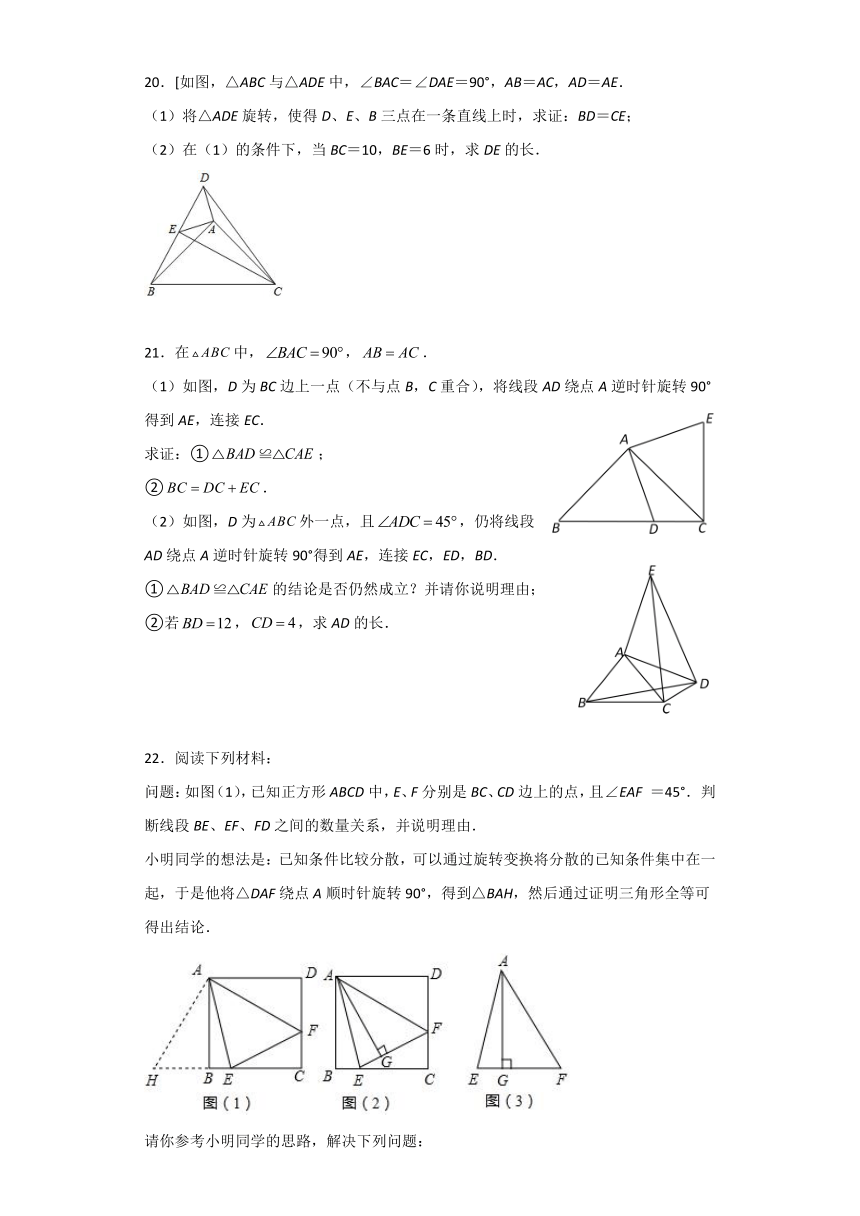
20.[如图,△ABC与△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.
(1)将△ADE旋转,使得D、E、B三点在一条直线上时,求证:BD=CE;
(2)在(1)的条件下,当BC=10,BE=6时,求DE的长.
21.在中,,.
(1)如图,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.
求证:①;
②.
(2)如图,D为外一点,且,仍将线段AD绕点A逆时针旋转90°得到AE,连接EC,ED,BD.
①的结论是否仍然成立?并请你说明理由;
②若,,求AD的长.
22.阅读下列材料:
问题:如图(1),已知正方形ABCD中,E、F分别是BC、CD边上的点,且∠EAF =45°. 判断线段BE、EF、FD之间的数量关系,并说明理由.
小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△DAF绕点A顺时针旋转90°,得到△BAH,然后通过证明三角形全等可得出结论.
请你参考小明同学的思路,解决下列问题:
(1)如图(1)中线段BE、EF、FD之间的数量关系是 ;
(2)如图(2),已知正方形ABCD边长为5,E、F分别是BC、CD边上的点,且∠EAF=45°,AG⊥EF于点G,则AG的长为 ,△EFC的周长为 ;
(3)如图(3),已知△AEF中,∠EAF=45°,AG⊥EF于点G,且EG=2,GF=3,求△AEF的面积.写出解答过程.
23.已知,在平面直角坐标系中,A,B两点的坐标分别为点A(3,0),点B(0,b),将线段AB绕点A顺时针旋转α°得到AC,连接BC.
(1)若α=90.
①如图1,b=1,直接写出点C的坐标;
②如图2,D为BC中点,连接OD.求证:OD平分∠AOB;
(2)如图3,若α=60,b=3,N为BC边上一点,M为AB延长线上一点,BM=CN,连接MN,将线段MN绕点N逆时针旋转120°得到NP,连接OP.求当∠AOP取何值时,线段OP最短
24.如图,抛物线y=-x2+bx+c与x轴交于A,B两点,其中A(3,0),B(-1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A、C,连接CD.
(1)分别求抛物线和直线AC的解析式;
(2)在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1,且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.
试卷第1页,共3页
参考答案
1.A
解:A、是中心对称图形,不是轴对称图形,故此选项符合题意;
B、既是中心对称图形,也是轴对称图形,故此选项不合题意;
C、是轴对称图形,不是中心对称图形,故此选项不合题意;
D、既不是中心对称图形,也不是轴对称图形,故此选项不合题意;
故选:A.
2.C
解:∵点A(n,5)与点B(-1,m)关于原点对称,
∴n=1,m=-5,
∴n-m=1-(-5)=6,
故选:C.
3.C
解:如图,点Q即为所求,;
故选C.
4.D
解:∵将△ABC绕点A逆时针旋转得到△AED,
∴∠D=∠C,
∵∠AED=∠CEF,
∴∠CFE=∠DAE=∠BAC=90°,
∴BC⊥DF,
故选:D.
5.D
解:由题意得:∠AOD=30°,OA=OD,
∴∠A=∠ADO75°.
故选D.
6.A
解:由旋转的性质可得,,,
∴,
∴,
∴,
∴,
故选A.
7.D
解: 将△ABC绕点C(0,﹣1)旋180°得到△ABC,
设 而
由中点坐标公式可得:
解得:
故选D
8.C
解:将ABP绕点A逆时针旋转后得到,
即
ABC是等腰直角三角形,
在中,
故选C
9.正三角形
解:正三角形是轴对称图形,但不是中心对称图形;
平行四边形不是轴对称图形,是中心对称图形;
菱形,矩形,正方形既是轴对称图形又是中心对称图形.
故答案为:正三角形.
10.120°; 150°
解:根据旋转的性质得,
,
,
,
根据题意,旋转角为,
.
故答案是:,.
11.
解:连接AD,
∵△ABC是边长为2的等边三角形,点D为BC边上的中点,
∴,,
在Rt△ABD中,AD==,
当点E在DA延长线上时,AE=DE AD.
此时AE取最小值,
∴在Rt△ADG中,AG=;
故答案为:.
12.
解:因为点与点关于原点对称,
∴,
所以,,
所以.
故答案为:-1.
13.
解:
将绕点按逆时针方向旋转得到.
,
故答案为:
14.
解:由旋转的性质得,,
,
,
点E,点B,点C三点共线,
,
,
,
,
,
,
正方形的周长为12,
,
,
,
设,则,
在中,,
,
解得,
,
故答案为:
15.1
解:(1)过P'点作CP垂线,垂足为D,如下图
∵CP'=2且∠P'CB=30°
∴P'D= =1
(2)由P'向CP作垂线,垂足为D,设BD为x
所构成的图形中△CDP',△BDP'都是直角三角形
所以P'B -BD =P'D =CP' -CD
又BP'=AB==
所以
解得x=
所以P'D==
16.40°
解:∵△ABC绕C点逆时针方向旋转得到△DEC,
∴AC=CD,
∴∠ADF=∠DAC=(180°-α),
∴∠DAF=∠ADC-∠BAC=(180°-α)-30°,
根据三角形的外角性质,∠AFD=∠BAC+∠DAC=30°+α,
△ADF是等腰三角形,分三种情况讨论,
①∠ADF=∠DAF时,(180°-α)=(180°-α)-30°,无解;
②∠ADF=∠AFD时,(180°-α)=30°+α,
解得α=40°,
③∠DAF=∠AFD时,(180°-α)-30°=30°+α,
解得α=20°,
综上所述,旋转角α度数为20°或40°.
故答案为:20°或40°.
17.解:(1)如图1,△DCE即为所求;
(2)如图2,△DCE即为所求.
18.(1)等边;(2);(3)
解:(1)∵将绕点顺时针旋转后得到,
∴,
是等边三角形
故答案为:等边
(2)
是等边三角形
是等边三角形
的周长为
(3),是等边三角形
,
19.(1)10;(2)
解:(1)由旋转的性质可得,,
∵,
∴.
∵是旋转得到的,
∴在中,根据勾股定理得.
(2)由(1)知,,由旋转的性质得,
∴是等边三角形.
∴.
又,
∴.
∴.
20.(1);(2)DE=2
证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠EAB=∠DAE+∠EAB,
即∠DAB=∠EAC,
在△ABD和△ACE中,
,
∴△DAB≌△EAC(SAS),
∴DB=EC;
(2)由(1)知△DAB≌△EAB,
∴∠DBA=∠ECA,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
即∠ABC+(∠BCE+∠ACE)=90°,
∴∠ABC+∠DBA+∠BCE=90°,
即∠DBA+∠BCE=90°,
∴∠BEC=90°,
∵BC=10,BE=6,
∴EC2=BC2 BE2=102 62=64,
∴EC=8,
∴DE=DB BE=DB CE=8 6=2.
21.(1)①;②;(2)①成立,理由;②8
解:(1)①证明:由旋转的性质得,,AE=AD,
∴,即.
在和中,
∴;
②由①知,
∴,
∴.
(2)①结论仍然成立.
理由:由旋转的性质得,,AE=AD,
∴,即,
在与中,
∴.
②由(2)①知,
∴.
∵线段AD绕点A逆时针旋转90°得到AE,
∴,,
∴.
∵,
∴.
∵在中,,
∴.
∵在中,由勾股定理得:,
∴,
∴.
22.(1);(2)5,10;(3)△AEF的面积为15.解答过程见解析.
解:(1),理由如下:
∵将△DAF绕点A顺时针旋转90°,得到△BAH
∴ △ ADF≌ △ ABH
∴ ∠ DAF=∠ BAH,AF=AH
∴∠FAH=90°
∴∠EAF=∠EAH=45°
在△FAE和△HAE中,
AF=AH
∠FAE=∠HAE
AE=AE
∴△FAE≌△HAE(SAS)
∴EF=HE=BE+HB
∴EF=BE+DF
(2)∵△FAE≌△HAE,AG、AB分别是△FAE与△HAE的高
∴ AG=AB=5
在△AEG与△ABE中,
∠AGE=∠ABE=90°
AE=AE
AG=AB
∴ Rt△AEG≌ Rt△ABE(HL)
∴EG=BE
同理GF=DF
∴△EFC的周长=EC+EF+FC=EC+EG+GF+FC=EC+BE+DF+FC=BC+CD=10
(3)将△AEF置于图2中,
∵EG=2,GF=3
∴BE=2,DF=3,EF=5
设AB=x,则CE=x-2,CF=x-3
在△CEF中,
∵∠C=90°
∴
故
解得(舍去),
∴AB=6
∴AG=AB=6
∴
23.(1)①;②;(2)时,线段OP最短
解:(1)①∵,
∴为等腰直角三角形,
过点作轴于点,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵A(3,0),点B(0,1),
∴,
∴点;
②∵点,点,
∴的中点的坐标为,
即,
过点作轴与轴交于点,
则可知,
∴为等腰直角三角形,
∴,
∴OD平分∠AOB;
(2)作交于点,
连接,过点作
交延长线于点,
∵,
∴,
∵是等边三角形,
∴,
∵,
∴,,
∴是等边三角形,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴点在直线上运动,
根据垂线段最短可知,当点和点重合时,的值最小,
此时.
24.(1)y=-x2+2x+3,y=-x+3;(2)存在,(-1,0)或(4,-5);(3)存在,(1,2)或(1,-3)
解:(1)把、代入,
解得、
∴抛物线的解析式为
则C点为(0,3),又,代入,
得,, ∴直线AC的解析式为,
(2)如图,连接BC,
∵点D是抛物线的对称轴与x轴的交点,
∴,
∴,
∵,
∴,此时,点P与点B重合,
即:,
过B点作交抛物线于点P,
则直线BP的解析式为①,
∵抛物线的解析式为②,
联立①②解得,或,
∴P(4,﹣5),
∴即点P的坐标为(﹣1,0)或(4,﹣5);
(3)由(1)可知,抛物线解析式为
把代入直线AC解析式
得AC与抛物线对称轴的交点,如下图所示:
,
即
则是等腰直角三角形,符合题意,
M点即为所求Q点的一种情况,
当Q点在x轴下方时,设Q为,,
因为线段AQ绕Q点顺时针旋转90°得到线段
过A1作直线DQ的垂线于E点,则
∴,
∴
∵点A1恰好落在抛物线上,
代入,解得m=-3或 (舍去)
∴Q(1,-3)
综上,Q点坐标为(1,2)或(1,-3)
一、单选题(满分40分)
1.下面四个图案中,是中心对称不是轴对称图形的是( )
A. B. C. D.
2.若点A(n,5)与点B(-1,m)关于原点对称,则( )
A.4 B.-4 C.6 D.- 6
3.如图,在平面直角坐标系中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,其中A、B、C分别和D、E、F对应,则旋转中心的坐标是( )
A.(0,0) B. C. D.
4.如图,在中,,将绕点逆时针旋转得到,使点的对应点恰好落在边上,点的对应点为,延长交于点,则下列结论一定正确的是( )
A. B. C. D.
5.如图,ODC是由OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数是( )
A.30° B.45° C.60° D.75°
6.如图,在△ABC中,∠ACB=45°,BC=1,AC=2,将△ABC绕点A逆时针旋转得到,其中点与点B是对应点,且点C、、在同一条直线上,则的长为( )
A.3 B.4 C.2.5 D.3
7.如图将△ABC绕点C(0,﹣1)旋转180°得到△ABC,设点的坐标为(a,b),则A的坐标为( )
A.(﹣a,﹣b) B.(﹣a,﹣b﹣1) C.(﹣a,﹣b+1) D.(﹣a,﹣b﹣2)
8.如图,ABC是等腰直角三角形,BC是斜边,将ABP绕点A逆时针旋转后得到,如果AP=2,那么的长等于( )
A. B. C. D.
二、填空题(满分40分)
9.在“正三角形,平行四边形,菱形,矩形,正方形”中,是轴对称图形但不是中心对称图形的是 _______.
10.如图, ABC绕点B旋转后到达△BDE处,若∠ABC=120°,∠CBD=30°,则∠DBE=_______,∠CBE=________________.
11.如图,△ABC是边长为2的等边三角形,点D为BC边上的中点,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为____.
12.在平面直角坐标系中,已知点与点关于原点对称.则______.
13.如图,在中,,将绕点按逆时针方向旋转得到.若点恰好落在边上,且,则的度数为______.
14.如图,点M,N分别在正方形ABCD的边BC,CD上,且把绕点A顺时针旋转得到,若正方形的周长为12,,则ME的长为______.
15.如图,在中,,,延长至点P,使,将线段绕点C逆时针旋转角得到,连结,.
(1)当时,点到直线的距离为_________;
(2)当时,点到直线的距离为_________.
16.如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转角(0°<<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角度数为__,△ADF是等腰三角形.
三、解答题(满分40分)
17.如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中,画出一个与△ABC成中心对称的格点三角形;
(2)在图2中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
18.如图,在等边中,点是边上一点,连接将绕点顺时针旋转后得到,连接.
(1)是_ 三角形;
(2)若,求的周长;
(3)求证:.
19.在中,,将绕点C顺时针旋转,得,D,E分别是点B,A的对应点.记旋转角为.
(1)如图①,连接AD,若,,,求AD的长;
(2)如图②,连接BD,若,求证:.
20.[如图,△ABC与△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.
(1)将△ADE旋转,使得D、E、B三点在一条直线上时,求证:BD=CE;
(2)在(1)的条件下,当BC=10,BE=6时,求DE的长.
21.在中,,.
(1)如图,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.
求证:①;
②.
(2)如图,D为外一点,且,仍将线段AD绕点A逆时针旋转90°得到AE,连接EC,ED,BD.
①的结论是否仍然成立?并请你说明理由;
②若,,求AD的长.
22.阅读下列材料:
问题:如图(1),已知正方形ABCD中,E、F分别是BC、CD边上的点,且∠EAF =45°. 判断线段BE、EF、FD之间的数量关系,并说明理由.
小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△DAF绕点A顺时针旋转90°,得到△BAH,然后通过证明三角形全等可得出结论.
请你参考小明同学的思路,解决下列问题:
(1)如图(1)中线段BE、EF、FD之间的数量关系是 ;
(2)如图(2),已知正方形ABCD边长为5,E、F分别是BC、CD边上的点,且∠EAF=45°,AG⊥EF于点G,则AG的长为 ,△EFC的周长为 ;
(3)如图(3),已知△AEF中,∠EAF=45°,AG⊥EF于点G,且EG=2,GF=3,求△AEF的面积.写出解答过程.
23.已知,在平面直角坐标系中,A,B两点的坐标分别为点A(3,0),点B(0,b),将线段AB绕点A顺时针旋转α°得到AC,连接BC.
(1)若α=90.
①如图1,b=1,直接写出点C的坐标;
②如图2,D为BC中点,连接OD.求证:OD平分∠AOB;
(2)如图3,若α=60,b=3,N为BC边上一点,M为AB延长线上一点,BM=CN,连接MN,将线段MN绕点N逆时针旋转120°得到NP,连接OP.求当∠AOP取何值时,线段OP最短
24.如图,抛物线y=-x2+bx+c与x轴交于A,B两点,其中A(3,0),B(-1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A、C,连接CD.
(1)分别求抛物线和直线AC的解析式;
(2)在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1,且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.
试卷第1页,共3页
参考答案
1.A
解:A、是中心对称图形,不是轴对称图形,故此选项符合题意;
B、既是中心对称图形,也是轴对称图形,故此选项不合题意;
C、是轴对称图形,不是中心对称图形,故此选项不合题意;
D、既不是中心对称图形,也不是轴对称图形,故此选项不合题意;
故选:A.
2.C
解:∵点A(n,5)与点B(-1,m)关于原点对称,
∴n=1,m=-5,
∴n-m=1-(-5)=6,
故选:C.
3.C
解:如图,点Q即为所求,;
故选C.
4.D
解:∵将△ABC绕点A逆时针旋转得到△AED,
∴∠D=∠C,
∵∠AED=∠CEF,
∴∠CFE=∠DAE=∠BAC=90°,
∴BC⊥DF,
故选:D.
5.D
解:由题意得:∠AOD=30°,OA=OD,
∴∠A=∠ADO75°.
故选D.
6.A
解:由旋转的性质可得,,,
∴,
∴,
∴,
∴,
故选A.
7.D
解: 将△ABC绕点C(0,﹣1)旋180°得到△ABC,
设 而
由中点坐标公式可得:
解得:
故选D
8.C
解:将ABP绕点A逆时针旋转后得到,
即
ABC是等腰直角三角形,
在中,
故选C
9.正三角形
解:正三角形是轴对称图形,但不是中心对称图形;
平行四边形不是轴对称图形,是中心对称图形;
菱形,矩形,正方形既是轴对称图形又是中心对称图形.
故答案为:正三角形.
10.120°; 150°
解:根据旋转的性质得,
,
,
,
根据题意,旋转角为,
.
故答案是:,.
11.
解:连接AD,
∵△ABC是边长为2的等边三角形,点D为BC边上的中点,
∴,,
在Rt△ABD中,AD==,
当点E在DA延长线上时,AE=DE AD.
此时AE取最小值,
∴在Rt△ADG中,AG=;
故答案为:.
12.
解:因为点与点关于原点对称,
∴,
所以,,
所以.
故答案为:-1.
13.
解:
将绕点按逆时针方向旋转得到.
,
故答案为:
14.
解:由旋转的性质得,,
,
,
点E,点B,点C三点共线,
,
,
,
,
,
,
正方形的周长为12,
,
,
,
设,则,
在中,,
,
解得,
,
故答案为:
15.1
解:(1)过P'点作CP垂线,垂足为D,如下图
∵CP'=2且∠P'CB=30°
∴P'D= =1
(2)由P'向CP作垂线,垂足为D,设BD为x
所构成的图形中△CDP',△BDP'都是直角三角形
所以P'B -BD =P'D =CP' -CD
又BP'=AB==
所以
解得x=
所以P'D==
16.40°
解:∵△ABC绕C点逆时针方向旋转得到△DEC,
∴AC=CD,
∴∠ADF=∠DAC=(180°-α),
∴∠DAF=∠ADC-∠BAC=(180°-α)-30°,
根据三角形的外角性质,∠AFD=∠BAC+∠DAC=30°+α,
△ADF是等腰三角形,分三种情况讨论,
①∠ADF=∠DAF时,(180°-α)=(180°-α)-30°,无解;
②∠ADF=∠AFD时,(180°-α)=30°+α,
解得α=40°,
③∠DAF=∠AFD时,(180°-α)-30°=30°+α,
解得α=20°,
综上所述,旋转角α度数为20°或40°.
故答案为:20°或40°.
17.解:(1)如图1,△DCE即为所求;
(2)如图2,△DCE即为所求.
18.(1)等边;(2);(3)
解:(1)∵将绕点顺时针旋转后得到,
∴,
是等边三角形
故答案为:等边
(2)
是等边三角形
是等边三角形
的周长为
(3),是等边三角形
,
19.(1)10;(2)
解:(1)由旋转的性质可得,,
∵,
∴.
∵是旋转得到的,
∴在中,根据勾股定理得.
(2)由(1)知,,由旋转的性质得,
∴是等边三角形.
∴.
又,
∴.
∴.
20.(1);(2)DE=2
证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠EAB=∠DAE+∠EAB,
即∠DAB=∠EAC,
在△ABD和△ACE中,
,
∴△DAB≌△EAC(SAS),
∴DB=EC;
(2)由(1)知△DAB≌△EAB,
∴∠DBA=∠ECA,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
即∠ABC+(∠BCE+∠ACE)=90°,
∴∠ABC+∠DBA+∠BCE=90°,
即∠DBA+∠BCE=90°,
∴∠BEC=90°,
∵BC=10,BE=6,
∴EC2=BC2 BE2=102 62=64,
∴EC=8,
∴DE=DB BE=DB CE=8 6=2.
21.(1)①;②;(2)①成立,理由;②8
解:(1)①证明:由旋转的性质得,,AE=AD,
∴,即.
在和中,
∴;
②由①知,
∴,
∴.
(2)①结论仍然成立.
理由:由旋转的性质得,,AE=AD,
∴,即,
在与中,
∴.
②由(2)①知,
∴.
∵线段AD绕点A逆时针旋转90°得到AE,
∴,,
∴.
∵,
∴.
∵在中,,
∴.
∵在中,由勾股定理得:,
∴,
∴.
22.(1);(2)5,10;(3)△AEF的面积为15.解答过程见解析.
解:(1),理由如下:
∵将△DAF绕点A顺时针旋转90°,得到△BAH
∴ △ ADF≌ △ ABH
∴ ∠ DAF=∠ BAH,AF=AH
∴∠FAH=90°
∴∠EAF=∠EAH=45°
在△FAE和△HAE中,
AF=AH
∠FAE=∠HAE
AE=AE
∴△FAE≌△HAE(SAS)
∴EF=HE=BE+HB
∴EF=BE+DF
(2)∵△FAE≌△HAE,AG、AB分别是△FAE与△HAE的高
∴ AG=AB=5
在△AEG与△ABE中,
∠AGE=∠ABE=90°
AE=AE
AG=AB
∴ Rt△AEG≌ Rt△ABE(HL)
∴EG=BE
同理GF=DF
∴△EFC的周长=EC+EF+FC=EC+EG+GF+FC=EC+BE+DF+FC=BC+CD=10
(3)将△AEF置于图2中,
∵EG=2,GF=3
∴BE=2,DF=3,EF=5
设AB=x,则CE=x-2,CF=x-3
在△CEF中,
∵∠C=90°
∴
故
解得(舍去),
∴AB=6
∴AG=AB=6
∴
23.(1)①;②;(2)时,线段OP最短
解:(1)①∵,
∴为等腰直角三角形,
过点作轴于点,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵A(3,0),点B(0,1),
∴,
∴点;
②∵点,点,
∴的中点的坐标为,
即,
过点作轴与轴交于点,
则可知,
∴为等腰直角三角形,
∴,
∴OD平分∠AOB;
(2)作交于点,
连接,过点作
交延长线于点,
∵,
∴,
∵是等边三角形,
∴,
∵,
∴,,
∴是等边三角形,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴点在直线上运动,
根据垂线段最短可知,当点和点重合时,的值最小,
此时.
24.(1)y=-x2+2x+3,y=-x+3;(2)存在,(-1,0)或(4,-5);(3)存在,(1,2)或(1,-3)
解:(1)把、代入,
解得、
∴抛物线的解析式为
则C点为(0,3),又,代入,
得,, ∴直线AC的解析式为,
(2)如图,连接BC,
∵点D是抛物线的对称轴与x轴的交点,
∴,
∴,
∵,
∴,此时,点P与点B重合,
即:,
过B点作交抛物线于点P,
则直线BP的解析式为①,
∵抛物线的解析式为②,
联立①②解得,或,
∴P(4,﹣5),
∴即点P的坐标为(﹣1,0)或(4,﹣5);
(3)由(1)可知,抛物线解析式为
把代入直线AC解析式
得AC与抛物线对称轴的交点,如下图所示:
,
即
则是等腰直角三角形,符合题意,
M点即为所求Q点的一种情况,
当Q点在x轴下方时,设Q为,,
因为线段AQ绕Q点顺时针旋转90°得到线段
过A1作直线DQ的垂线于E点,则
∴,
∴
∵点A1恰好落在抛物线上,
代入,解得m=-3或 (舍去)
∴Q(1,-3)
综上,Q点坐标为(1,2)或(1,-3)
同课章节目录
