2021-2022学年人教版九年级数学下册第二十七章相似单元测试卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十七章相似单元测试卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 12:11:53 | ||
图片预览


文档简介
人教版九年级数学下册
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如果两个相似三角形对应边中线之比是1∶4,那么它们的对应高之比是( )
A.1∶2 B.1∶4 C.1∶8 D.1∶16
2. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.= B.= C.= D.=
3. 如图,在△ABC中,DE∥BC,=,BC=12,则DE的长是( )
A.3 B.4 C.5 D.6
4. 如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是( )
A.2 B.3 C.4 D.5
5. 如图,将平行四边形AEFG变换到平行四边形ABCD,其中E,G分别是AB,AD的中点,下列叙述不正确的是( )
A.这种变换是位似变换 B.对应边扩大到原来的2倍
C.各对应角度数不变 D.面积扩大到原来的2倍
6. 两个相似三角形的最短边长分别是5 cm和3 cm,它们的周长之差为12 cm,那么较小三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
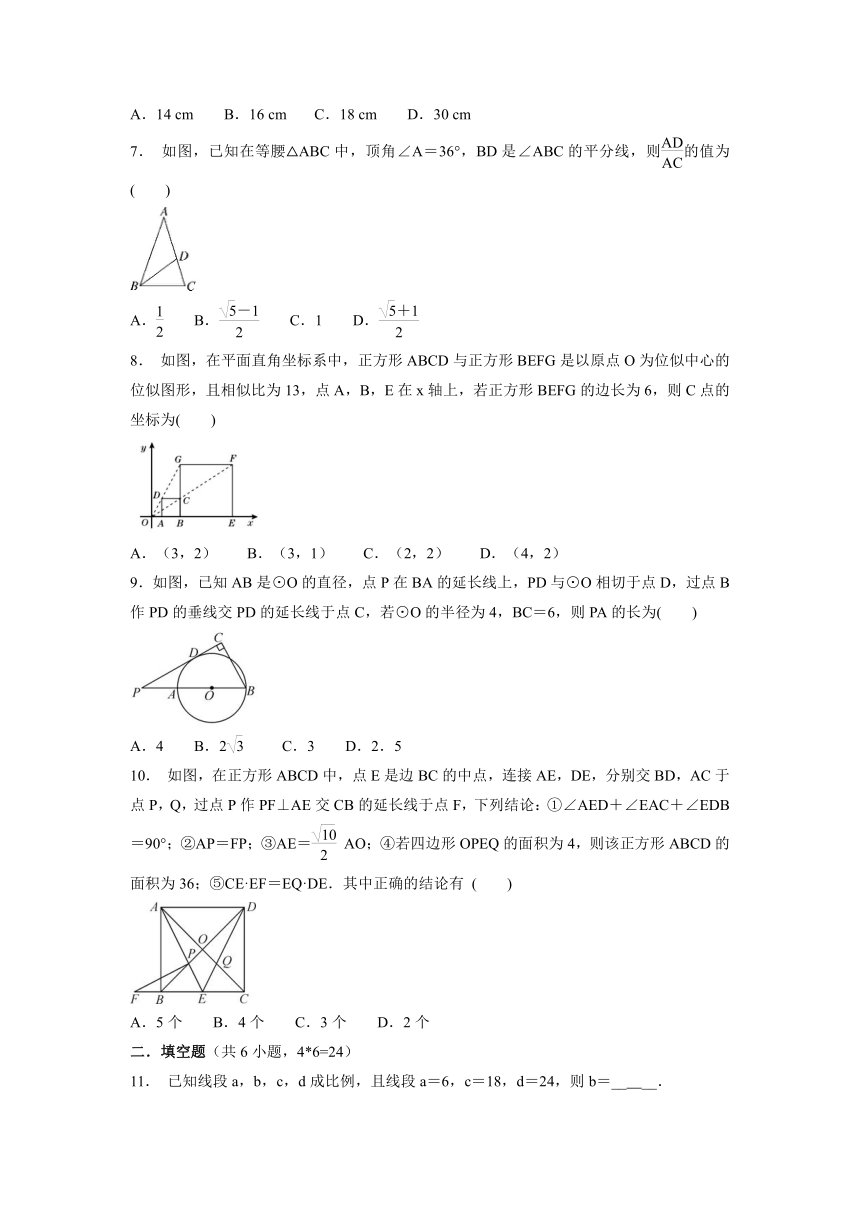
7. 如图,已知在等腰△ABC中,顶角∠A=36°,BD是∠ABC的平分线,则的值为( )
A. B. C.1 D.
8. 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为13,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点的坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
9.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( )
A.4 B.2 C.3 D.2.5
10. 如图,在正方形ABCD中,点E是边BC的中点,连接AE,DE,分别交BD,AC于点P,Q,过点P作PF⊥AE交CB的延长线于点F,下列结论:①∠AED+∠EAC+∠EDB=90°;②AP=FP;③AE=AO;④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36;⑤CE·EF=EQ·DE.其中正确的结论有 ( )
A.5个 B.4个 C.3个 D.2个
二.填空题(共6小题,4*6=24)
11. 已知线段a,b,c,d成比例,且线段a=6,c=18,d=24,则b=__ __.
12. 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF=_____.
13. 在△ABC中,AB=8,AC=6,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,则需要添加一个条件是 .(写出一种情况即可)
14. 如图,△ABC在平面直角坐标系中,以原点O为位似中心,将△ABC放大到原来的2倍得到△A′B′C′,那么落在第四象限的点A′的坐标是________.
15.如图,在△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠B,CD=2,点E是线段BC延长线上一动点,则当CE的长为_____时,△DCE和△ABC相似.
16.)如图,在Rt△ABC中,∠C=90°,AB的垂直平分线分别交AB,AC于点D,E,BE=8,⊙O为△BCE的外接圆,过点E作⊙O的切线EF交AB于点F,则下列结论正确的是__________.(写出所有正确结论的序号)
①AE=BC;②∠AED=∠CBD;
③若∠DBE=40°,则的长为;④=;⑤若EF=6,则CE=2.24.
三.解答题(共5小题, 56分)
17.(6分) 如图,在△ABC中,DE∥BC,DE=2,BC=3.求的值.
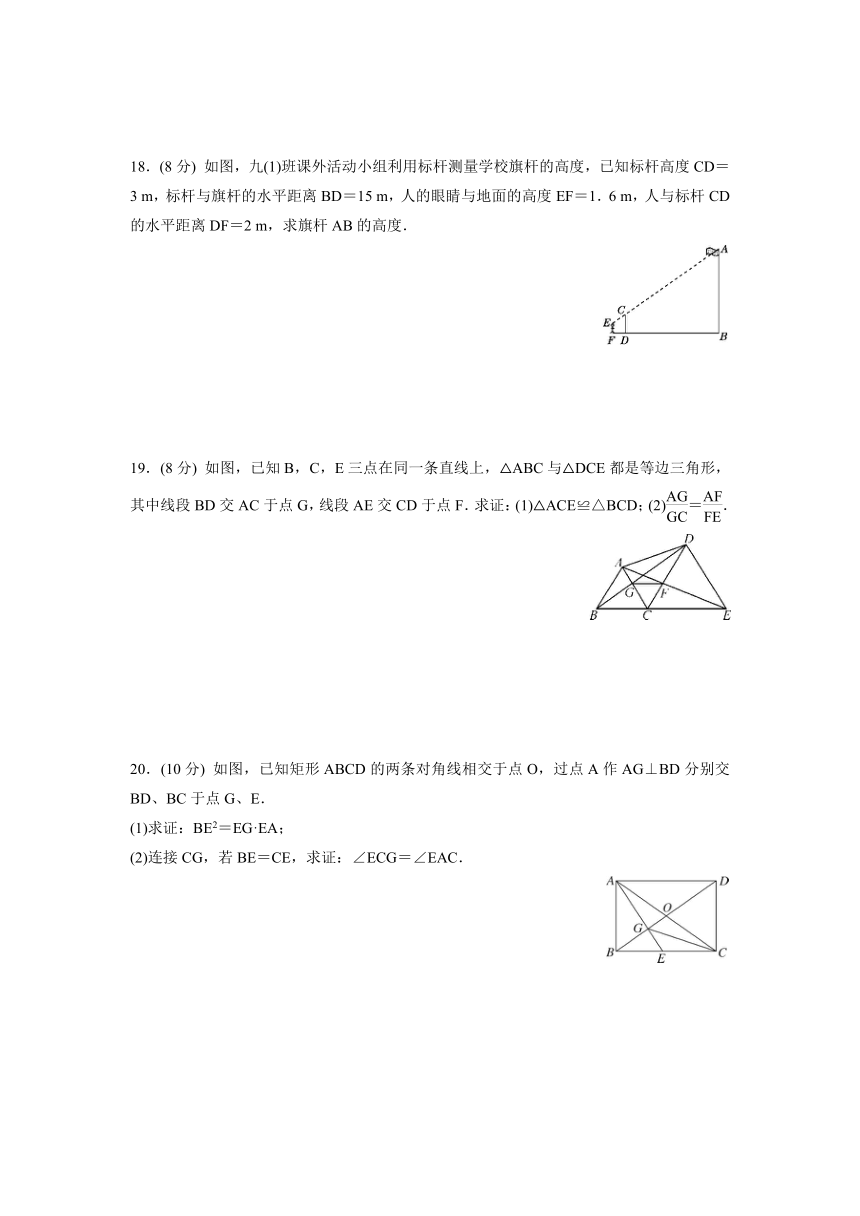
18.(8分) 如图,九(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6 m,人与标杆CD的水平距离DF=2 m,求旗杆AB的高度.
19.(8分) 如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)=.
20.(10分) 如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E.
(1)求证:BE2=EG·EA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
21.(12分) 有一块锐角三角形卡纸余料ABC,它的边BC=120 cm,高AD=80 cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2:5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片一边在矩形纸片的较长边EH上,其余顶点分别在AB,AC上,具体裁剪方式如图所示,AD交PQ于K,交EH于R.
(1)求矩形纸片较长边EH的长;
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料△AEH中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
22.(12分) 已知正方形ABCD,点E在边CD上,点F在线段BE的延长线上,连接FC,且∠FCE=∠CBE.
(1)如图①,当点E为CD边的中点时,求证:CF=2EF;
(2)如图②,当点F位于线段AD的延长线上时,求证:=.
参考答案
1-5BDBCD 6-10CBAAB
11.8
12.4
13.∠A=∠D(或BC∶EF=2∶1)
14.(2,-4)
15.3或
16.②④⑤
17. 解:∵DE∥BC,∴△ADE∽△ABC,∴==.
18. 解:作EH⊥AB于点H,交CD于点G.∵CD⊥FB,AB⊥FB,∴CD∥AB.∴△CGE∽△AHE.∴=,即=.∴=,解得AH=11.9 m.∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).答:旗杆AB的高度为13.5 m.
19. 解:(1)∵△ABC与△CDE都是等边三角形,∴AC=BC,CE=CD,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,可证△ACE≌△BCD(SAS) (2)∵△ACE≌△BCD,∴∠AEC=∠BDC,可证△GCD≌△FCE(ASA),∴CG=CF,∴△CFG为等边三角形,∴∠CGF=∠ACB=60°,∴GF∥CE,∴=
20. 证明:(1)∵四边形ABCD是矩形,∴∠ABC=90°.∵AE⊥BD,∴∠BGE=∠ABC=90°.∵∠BEG=∠AEB,∴△ABE∽△BGE,∴=,∴BE2=EG·EA.
(2)由(1)得BE2=EG·EA.∵BE=CE,∴CE2=EG·EA,∴=.又∵∠CEG=∠AEC,∴△CEG∽△AEC,∴∠ECG=∠EAC.
21. 解:(1)设EF=2x cm,EH=5x cm.∵四边形EFGH是矩形,∴EH∥BC,∴△AEH∽△ABC,∴=,即=,解得x=15,∴EH=15×5=75(cm),∴矩形纸片较长边EH的长为75 cm.
(2)小聪的剪法不正确.理由如下:设正方形的边长为a cm,AR=AD-RD=80-2×15=50(cm),AK=(50-a)cm,由题意,知△APQ∽△AEH,∴=,即=,解得a=30,与边EH平行的中位线=×75=37.5(cm).∵37.5≠30,∴小聪的剪法不正确.
22. 证明:(1)∵四边形ABCD是正方形,∴CD=BC.∵点E为CD边的中点,∴CE=CD=BC.∵∠FCE=∠CBE,∠F=∠F,∴△FCE∽△FBC,∴=.又∵CE=BC,∴=,∴CF=2EF.
(2)∵四边形ABCD是正方形,∴DE∥AB,AD∥BC,AD=CD,∴=,∴=.∵AF∥BC,∴∠DFE=∠CBE.∵∠FCE=∠CBE,∴∠DFE=∠FCE.又∵∠FDE=∠CDF,∴△FDE∽△CDF,∴=,∴=.
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如果两个相似三角形对应边中线之比是1∶4,那么它们的对应高之比是( )
A.1∶2 B.1∶4 C.1∶8 D.1∶16
2. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.= B.= C.= D.=
3. 如图,在△ABC中,DE∥BC,=,BC=12,则DE的长是( )
A.3 B.4 C.5 D.6
4. 如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是( )
A.2 B.3 C.4 D.5
5. 如图,将平行四边形AEFG变换到平行四边形ABCD,其中E,G分别是AB,AD的中点,下列叙述不正确的是( )
A.这种变换是位似变换 B.对应边扩大到原来的2倍
C.各对应角度数不变 D.面积扩大到原来的2倍
6. 两个相似三角形的最短边长分别是5 cm和3 cm,它们的周长之差为12 cm,那么较小三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
7. 如图,已知在等腰△ABC中,顶角∠A=36°,BD是∠ABC的平分线,则的值为( )
A. B. C.1 D.
8. 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为13,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点的坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
9.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则PA的长为( )
A.4 B.2 C.3 D.2.5
10. 如图,在正方形ABCD中,点E是边BC的中点,连接AE,DE,分别交BD,AC于点P,Q,过点P作PF⊥AE交CB的延长线于点F,下列结论:①∠AED+∠EAC+∠EDB=90°;②AP=FP;③AE=AO;④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36;⑤CE·EF=EQ·DE.其中正确的结论有 ( )
A.5个 B.4个 C.3个 D.2个
二.填空题(共6小题,4*6=24)
11. 已知线段a,b,c,d成比例,且线段a=6,c=18,d=24,则b=__ __.
12. 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF=_____.
13. 在△ABC中,AB=8,AC=6,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,则需要添加一个条件是 .(写出一种情况即可)
14. 如图,△ABC在平面直角坐标系中,以原点O为位似中心,将△ABC放大到原来的2倍得到△A′B′C′,那么落在第四象限的点A′的坐标是________.
15.如图,在△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠B,CD=2,点E是线段BC延长线上一动点,则当CE的长为_____时,△DCE和△ABC相似.
16.)如图,在Rt△ABC中,∠C=90°,AB的垂直平分线分别交AB,AC于点D,E,BE=8,⊙O为△BCE的外接圆,过点E作⊙O的切线EF交AB于点F,则下列结论正确的是__________.(写出所有正确结论的序号)
①AE=BC;②∠AED=∠CBD;
③若∠DBE=40°,则的长为;④=;⑤若EF=6,则CE=2.24.
三.解答题(共5小题, 56分)
17.(6分) 如图,在△ABC中,DE∥BC,DE=2,BC=3.求的值.
18.(8分) 如图,九(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6 m,人与标杆CD的水平距离DF=2 m,求旗杆AB的高度.
19.(8分) 如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)=.
20.(10分) 如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E.
(1)求证:BE2=EG·EA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
21.(12分) 有一块锐角三角形卡纸余料ABC,它的边BC=120 cm,高AD=80 cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2:5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片一边在矩形纸片的较长边EH上,其余顶点分别在AB,AC上,具体裁剪方式如图所示,AD交PQ于K,交EH于R.
(1)求矩形纸片较长边EH的长;
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料△AEH中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
22.(12分) 已知正方形ABCD,点E在边CD上,点F在线段BE的延长线上,连接FC,且∠FCE=∠CBE.
(1)如图①,当点E为CD边的中点时,求证:CF=2EF;
(2)如图②,当点F位于线段AD的延长线上时,求证:=.
参考答案
1-5BDBCD 6-10CBAAB
11.8
12.4
13.∠A=∠D(或BC∶EF=2∶1)
14.(2,-4)
15.3或
16.②④⑤
17. 解:∵DE∥BC,∴△ADE∽△ABC,∴==.
18. 解:作EH⊥AB于点H,交CD于点G.∵CD⊥FB,AB⊥FB,∴CD∥AB.∴△CGE∽△AHE.∴=,即=.∴=,解得AH=11.9 m.∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).答:旗杆AB的高度为13.5 m.
19. 解:(1)∵△ABC与△CDE都是等边三角形,∴AC=BC,CE=CD,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,可证△ACE≌△BCD(SAS) (2)∵△ACE≌△BCD,∴∠AEC=∠BDC,可证△GCD≌△FCE(ASA),∴CG=CF,∴△CFG为等边三角形,∴∠CGF=∠ACB=60°,∴GF∥CE,∴=
20. 证明:(1)∵四边形ABCD是矩形,∴∠ABC=90°.∵AE⊥BD,∴∠BGE=∠ABC=90°.∵∠BEG=∠AEB,∴△ABE∽△BGE,∴=,∴BE2=EG·EA.
(2)由(1)得BE2=EG·EA.∵BE=CE,∴CE2=EG·EA,∴=.又∵∠CEG=∠AEC,∴△CEG∽△AEC,∴∠ECG=∠EAC.
21. 解:(1)设EF=2x cm,EH=5x cm.∵四边形EFGH是矩形,∴EH∥BC,∴△AEH∽△ABC,∴=,即=,解得x=15,∴EH=15×5=75(cm),∴矩形纸片较长边EH的长为75 cm.
(2)小聪的剪法不正确.理由如下:设正方形的边长为a cm,AR=AD-RD=80-2×15=50(cm),AK=(50-a)cm,由题意,知△APQ∽△AEH,∴=,即=,解得a=30,与边EH平行的中位线=×75=37.5(cm).∵37.5≠30,∴小聪的剪法不正确.
22. 证明:(1)∵四边形ABCD是正方形,∴CD=BC.∵点E为CD边的中点,∴CE=CD=BC.∵∠FCE=∠CBE,∠F=∠F,∴△FCE∽△FBC,∴=.又∵CE=BC,∴=,∴CF=2EF.
(2)∵四边形ABCD是正方形,∴DE∥AB,AD∥BC,AD=CD,∴=,∴=.∵AF∥BC,∴∠DFE=∠CBE.∵∠FCE=∠CBE,∴∠DFE=∠FCE.又∵∠FDE=∠CDF,∴△FDE∽△CDF,∴=,∴=.
