2021-2022学年人教版七年级数学上册第4章几何图形初步 寒假自主提升训练(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册第4章几何图形初步 寒假自主提升训练(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 120.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 14:59:13 | ||
图片预览




文档简介
2021-2022学年人教版七年级数学上册《第4章几何图形初步》寒假自主提升训练(附答案)
1.如图,下列说法中正确的是( )
A.OA的方向是北偏东30° B.OB的方向是北偏西60°
C.OC的方向是南偏西15° D.OC的方向是南偏西75°
2.在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69° B.111° C.141° D.159°
3.如图,OA为北偏东44°方向,∠AOB=90°,则OB的方向为( )
A.南偏东46° B.南偏东44° C.南偏西44° D.北偏东46°
4.如图,甲从A处出发沿北偏东60°向走向B处,乙从A处出发沿南偏西30°方向走到C处,则∠BAC的度数是( )
A.160° B.150° C.120° D.90°
5.已知一个角的补角的一半比这个角小30°,求这个的余角.
6.一个角的补角比这个角的余角的3倍少10°,求这个角的度数.
7.已知一个角的补角比这个角的余角的3倍大20°,求这个角的度数.
8.若一个角的补角是这个角的余角的3倍,求这个角的度数.
9.若一个角的余角的3倍与这个角的补角的和为250°,试求这个角的度数.
10.如图,已知点A、B、C在同一直线上,线段AC=12,BC=16,点M、N分别是AC、BC的中点,求MN的长度.
11.(1)如图,已知点C在线段AB上,AC=8cm,BC=6cm,M,N分别是AC,BC的中点,求线段MN的长度;
(2)在(1)题中,如果AC=acm,BC=bcm,其他条件不变,求此时线段MN的长度.
12.如图,已知线段MN=8cm,C为AB上一点,且AC:CB=3:5,M,N分别为AC、AB的中点,求AB的长.
13.如图,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=12cm,AM=5cm,求BC的长;
(2)如果MN=8cm,求AB的长.
14.已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若线段AC=4,BC=6,则线段MN= ;
(2)若AB=m,求线段MN的长度.
15.如图,M为线段AB的中点,点C在线段BM上且CM:CB=1:2.若AB=12,求线段AC的长.
16.如图,已知点C在线段AB上,点M为AB的中点,AB=12,MC=2CB.求AC的长.
17.先画图,再解答:
(1)画线段AB,在线段AB的反向延长线上取一点C,使,再取AB得中点D;(注:非尺规作图)
(2)在(1)中,若C、D两点间的距离为6cm,求线段AB的长.
18.如图,线段AC=6cm,线段AB=21cm,M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
19.如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB,延长线段BA到D,使AD:AC=4:3,点M是BD的中点,求线段BD和AM的长度.
20.如图,已知点M是线段AB的中点,点E将AB分成AE:EB=3:4的两段,若EM=2cm,求线段AB的长度.
21.如图,已知线段a和线段AB,
(1)延长线段AB到C,使BC=a(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AB=5,BC=3,点O是线段AC的中点,求线段OB的长.
22.(1)钟表上2时15分时,时针与分针所成的锐角的度数是多少?
(2)若时针由2点30分走到2点55分,问分针转过多大的角度?
23.钟面上的角的问题.
(1)3点45分,时针与分针的夹角是多少?
(2)在9点与10点之间,什么时候时针与分针成100°的角?
24.在3点20分时,时钟的分针与时针的夹角为多少度?过多少分钟后它们的夹角为130°?
25.如图,已知∠AOB=90°,∠COD=90°,OE为∠BOD的平分线,∠BOE=17°,求∠AOC的度数.
26.如图1,∠AOB=∠COD=90°.
(1)若∠BOC=2∠AOC,求∠BOC的大小;
(2)试探究∠BOC与∠DOA之间的数量关系;
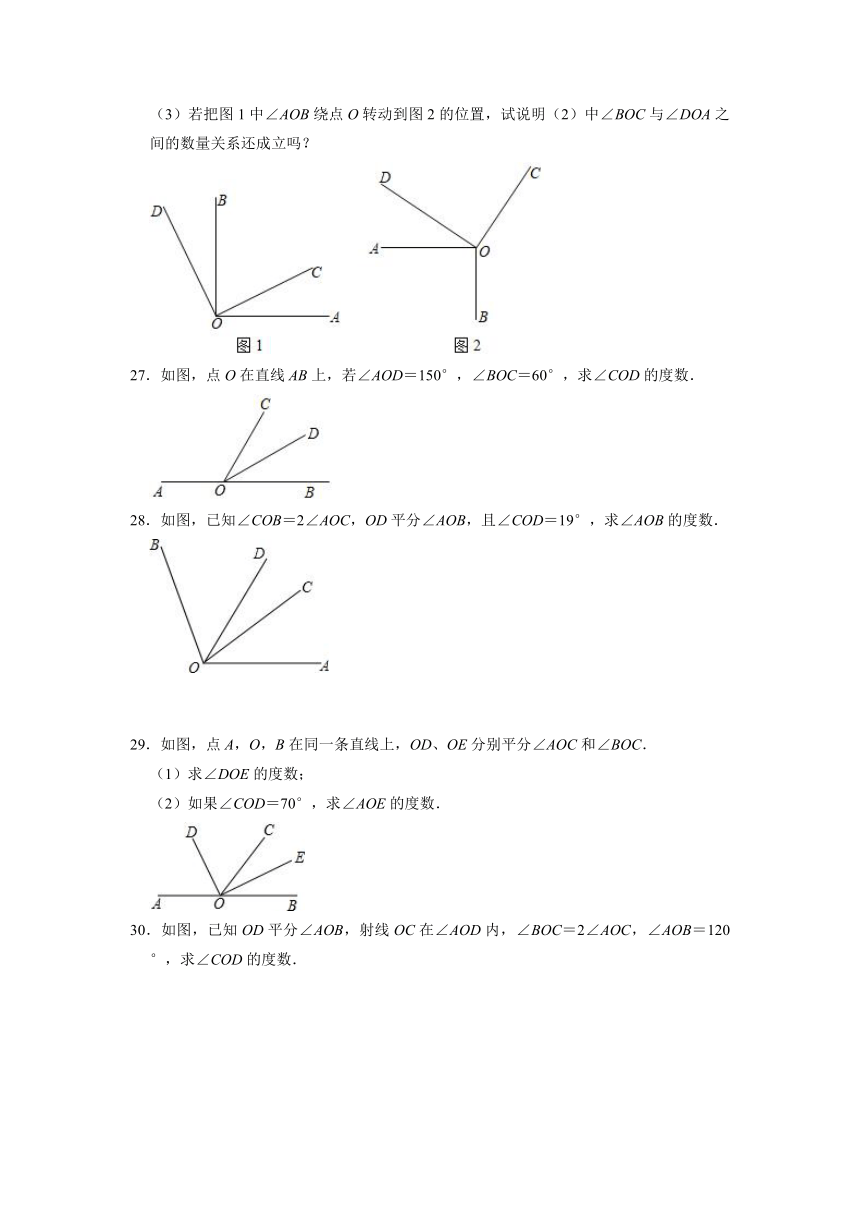
(3)若把图1中∠AOB绕点O转动到图2的位置,试说明(2)中∠BOC与∠DOA之间的数量关系还成立吗?
27.如图,点O在直线AB上,若∠AOD=150°,∠BOC=60°,求∠COD的度数.
28.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=19°,求∠AOB的度数.
29.如图,点A,O,B在同一条直线上,OD、OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=70°,求∠AOE的度数.
30.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=120°,求∠COD的度数.
31.如图所示,直线AE上有一点O,∠AOB=30°,∠BOC=∠AOB.
(1)求∠EOC的度数;
(2)如果OD平分∠EOC,求∠BOD的度数.
参考答案
1.解:由方向角的定义可知,
OA的方向是北偏东90°﹣30°=60°,因此选项A不符合题意;
OB的方向是北偏西90°﹣60°=30°,因此选项B不符合题意;
OC的方向是南偏西90°﹣15°=75°,因此选项C不符合题意;选项D符合题意;
故选:D.
2.解:由题意得:∠1=54°,∠2=15°,
∠3=90°﹣54°=36°,
∠AOB=36°+90°+15°=141°,
故选:C.
3.解:如图,
∵∠AOB=90°,
∴∠1+∠2=90°,
∴∠2=90°﹣∠1=90°﹣44°=46°,
∴OB的方向是南偏东46°,
故选:A.
4.解:由方向角的意义可知,∠NAB=60°,∠SAC=30°,
∴∠BOE=90°﹣60°=30°,
∴∠BAC=∠BAE+∠EAS+∠SAC
=30°+90°+30°
=150°,
故选:B.
5.解:设这个角的度数为x°,
依题意得(180﹣x)=x﹣30,
解得x=80,
90°﹣80°=10°.
答:这个角的余角为10°.
6.解:设这个角为x,
由题意得,180°﹣x=3(90°﹣x)﹣10°,
解得x=40°.
答:这个角的度数为40°.
7.解:设这个角是x°,
则(180﹣x)﹣3(90﹣x)=20,
解得x=55.
答:这个角的度数为55°.
8.解:设这个角是x,
则这个角的补角为180°﹣x,余角为90°﹣x,
所以3(90°﹣x)=180°﹣x,
整理,可得2x=90°,
解得:x=45°,
即这个角的度数为45°.
9.解:设这个角的度数为n°,由题意得:
3(90﹣n)+(180﹣n)=250,
解得:n=50.
经检验n=50符合题意,
答:这个角的度数为50°.
10.解:点M、N分别是AC、BC的中点,AC=12,BC=16,
MC=AC÷2=12÷2=6,
NC=CB÷2=16÷2=8,
由线段的和差,得
MN=MC+NC
=6+8
=14.
∴线段MN的长是14.
11.解:(1)∵AC=8cm,点M是AC的中点,
∴CM=AC=4cm,
∵BC=6cm,点N是BC的中点,
∴CN=BC=3cm,
∴MN=CM+CN=7cm,
∴线段MN的长度为7cm;
(2)∵点M、N分别是AC、BC的中点,
∴CM=AC,CN=BC,
∵AC=acm,BC=bcm,
∴MN=(AC+BC)=cm.
12.解:∵M、N分别为AC、AB的中点,
∴AC=2AM,AB=2AN,
∴AB﹣AC=2AN﹣2AM=2MN=16cm,
∵AC:CB=3:5,
∴AB=16÷(3+5﹣3)×(3+5)=25.6(cm).
故AB的长是25.6cm.
13.解:(1)∵点M是线段AC的中点,
∴AC=2AM,
∵AM=5cm,
∴AC=10cm,
∵AB=12cm,
∴BC=AB﹣AC=2cm;
(2)∵点M是线段AC的中点,点N是线段BC的中点,
∴BC=2NC,AC=2MC,
∵MN=NC+MC=8cm,
∴AB=BC+AC=2MN=2×8=16cm.
14.解:(1)∵N是BC的中点,M是AC的中点,AC=4,BC=6,
∴MC=2,CN=3,
∴MN=MC+CN=2+3=5;
(2)∵M是AC的中点,N是BC的中点,AB=m,
∴NM=MC+CN=AB=m.
故答案为:5.
15.解:∵M为线段AB的中点,AB=12,
∴AM=BM=AB=×12=6.
∵CM:CB=1:2,
∴CM=BM=×6=2.
∴AC=AM+CM=6+2=8.
16.解:∵点M为AB的中点,AB=12.
∴.
∵MC=2CB.
∴.
∴AC=AM+MC=10.
17.解:(1)根据题意画图如下:
(2)∵点D是AB的中点,
∴AD=AB,
∵AB=AC,
∴CD=5AD,
∵CD=6cm,
∴AD=cm,
∴AB=cm.
18.解:因为M是AC的中点,AC=6cm,
所以(cm).
因为AC=6cm,AB=21cm,
所以BC=AB﹣AC=15(cm),
因为CN:NB=1:2,
所以(cm),
所以MN=MC+CN=3+5=8(cm).
所以MN的长为8cm.
19.解:∵AB=3cm,BC=2AB,
∴BC=6(cm),
∴AC=AB+BC=9(cm),
∵AD:AC=4:3,
∴AD=9×=12(cm),
∴BD=AD+AB=15(cm),
∵点M是BD的中点,
∴BM=BD=(cm),
∴AM=BM﹣AB=﹣3=(cm).
20.解:设AB=x,则AM=x,AE=x,
根据题意得,x﹣x=2,
解得:x=28,
答:线段AB的长度为28cm.
21.解:(1)如图:
(2)∵AB=5,BC=3,
∴AC=8,
∵点O是线段AC的中点,
∴AO=CO=4,
∴BO=AB﹣AO=5﹣4=1,
∴OB长为1.
22.解:(1)2点15分时分针指向数字3,而时针从数字2开始转动的角度为15×0.5°=7.5°,
所以钟表上2时15分时,时针与分针所成的锐角的度数为30°﹣7.5°=22.5°;
(2)分针转过的角度为25×6°=150°.
23.解:(1)如图,∵由3点到3点45分,分针转了270°,时针转了270°×,
∴时针与分针的夹角是:180°﹣270°×=157.5°;
(2)设分针转的度数为x,则时针转的度数为,
得①90°+x﹣=100°,
解得,x=°,
°÷6°=(分);
②90°+﹣(x﹣180°)=100°,
解得,x=°,
°÷6°=(分);
∴9点过或分钟时,时针与分针成100°的角.
24.解:3点20分,时钟的分针与时针的夹角20×6﹣(3×30+0.5×20)=120﹣100=20°;
设过x分钟后它们的夹角为130°,得
6x+20﹣x=130,
解得x=20,
故过20分钟后它们的夹角为130°.
25.解:∵OE为∠BOD的平分线,∠BOE=17°,
∴∠BOD=2∠BOE=34°.
∴∠AOC=360°﹣∠AOB﹣∠COD﹣∠BOD=360°﹣90°﹣90°﹣34°=146°.
26.解:(1)∵∠BOC=2∠AOC,∠AOB=90°,
∴∠BOC+∠AOC=90°,
∵∠BOC=2∠AOC,
∴∠BOC=60°;
(2)∵∠COD=90°,
∴∠AOD=∠COD+∠AOC=90°+∠AOC,
∵∠AOB=90°,
∴∠BOC+∠AOC=90°,
∴∠BOC+∠AOD=∠BOC+90°+∠AOC=90°+90°=180°,
即∠BOC与∠AOD互为补角;
(3)成立.
∵∠AOB=∠COD=90°,
∴∠AOB+∠COD=180°,
∵∠BOC+∠AOD+∠AOB+∠COD=360°,
∴∠BOC+∠AOD=180°,
即∠BOC与∠AOD互为补角.
27.解:∵∠AOD=150°,∠BOC=60°,
∴∠COD=∠AOD+∠BOC﹣∠AOB=150°+60°﹣180°=30°.
28.解:设∠AOC=x,则∠COB=2x,
∴∠AOB=∠AOC+∠BOC=3x.
∵OD平分∠AOB,
∴∠AOD=∠AOB=.
∵∠COD=19°,
∴∠AOD﹣∠AOC=19°,
即=19.
解得:x=38.
∴∠AOB=3x=114°.
29.解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOC=∠AOC,∠COE=∠BOC,
∴∠DOE=∠DOC+∠COE=(∠AOC+∠BOC).
∵点A,O,B在同一条直线上,
∴∠AOC+∠BOC=180°.
∴∠DOE=×180°=90°.
(2))∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOC=∠AOC,∠COE=∠BOC,
∵∠COD=70°,
∴∠AOC=140°.
∴∠BOC=180°﹣∠AOC=40°.
∴∠COE=∠BOC=20°.
∴∠AOE=∠AOC+∠COE=140°+20°=160°.
30.解:∵OD平分∠AOB,∠AOB=120°,
∴∠AOD=∠AOB=×120°=60°,
∵∠BOC=2∠AOC,∠AOB=120°,
∴∠AOC=∠AOB=×120°=40°,
∴∠COD=∠AOD﹣∠AOC=60°﹣40°=20°.
31.解:(1)∵∠AOB=30°,∠BOC=∠AOB,
∴∠AOC=2∠AOB=60°,
∴∠EOC=120°.
(2)∵∠EOC=120°,OD平分∠EOC,
∴∠COD=∠EOC=60°,
∴∠BOD=∠COB+∠COD=30°+60°=90°.
1.如图,下列说法中正确的是( )
A.OA的方向是北偏东30° B.OB的方向是北偏西60°
C.OC的方向是南偏西15° D.OC的方向是南偏西75°
2.在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69° B.111° C.141° D.159°
3.如图,OA为北偏东44°方向,∠AOB=90°,则OB的方向为( )
A.南偏东46° B.南偏东44° C.南偏西44° D.北偏东46°
4.如图,甲从A处出发沿北偏东60°向走向B处,乙从A处出发沿南偏西30°方向走到C处,则∠BAC的度数是( )
A.160° B.150° C.120° D.90°
5.已知一个角的补角的一半比这个角小30°,求这个的余角.
6.一个角的补角比这个角的余角的3倍少10°,求这个角的度数.
7.已知一个角的补角比这个角的余角的3倍大20°,求这个角的度数.
8.若一个角的补角是这个角的余角的3倍,求这个角的度数.
9.若一个角的余角的3倍与这个角的补角的和为250°,试求这个角的度数.
10.如图,已知点A、B、C在同一直线上,线段AC=12,BC=16,点M、N分别是AC、BC的中点,求MN的长度.
11.(1)如图,已知点C在线段AB上,AC=8cm,BC=6cm,M,N分别是AC,BC的中点,求线段MN的长度;
(2)在(1)题中,如果AC=acm,BC=bcm,其他条件不变,求此时线段MN的长度.
12.如图,已知线段MN=8cm,C为AB上一点,且AC:CB=3:5,M,N分别为AC、AB的中点,求AB的长.
13.如图,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=12cm,AM=5cm,求BC的长;
(2)如果MN=8cm,求AB的长.
14.已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若线段AC=4,BC=6,则线段MN= ;
(2)若AB=m,求线段MN的长度.
15.如图,M为线段AB的中点,点C在线段BM上且CM:CB=1:2.若AB=12,求线段AC的长.
16.如图,已知点C在线段AB上,点M为AB的中点,AB=12,MC=2CB.求AC的长.
17.先画图,再解答:
(1)画线段AB,在线段AB的反向延长线上取一点C,使,再取AB得中点D;(注:非尺规作图)
(2)在(1)中,若C、D两点间的距离为6cm,求线段AB的长.
18.如图,线段AC=6cm,线段AB=21cm,M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
19.如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB,延长线段BA到D,使AD:AC=4:3,点M是BD的中点,求线段BD和AM的长度.
20.如图,已知点M是线段AB的中点,点E将AB分成AE:EB=3:4的两段,若EM=2cm,求线段AB的长度.
21.如图,已知线段a和线段AB,
(1)延长线段AB到C,使BC=a(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AB=5,BC=3,点O是线段AC的中点,求线段OB的长.
22.(1)钟表上2时15分时,时针与分针所成的锐角的度数是多少?
(2)若时针由2点30分走到2点55分,问分针转过多大的角度?
23.钟面上的角的问题.
(1)3点45分,时针与分针的夹角是多少?
(2)在9点与10点之间,什么时候时针与分针成100°的角?
24.在3点20分时,时钟的分针与时针的夹角为多少度?过多少分钟后它们的夹角为130°?
25.如图,已知∠AOB=90°,∠COD=90°,OE为∠BOD的平分线,∠BOE=17°,求∠AOC的度数.
26.如图1,∠AOB=∠COD=90°.
(1)若∠BOC=2∠AOC,求∠BOC的大小;
(2)试探究∠BOC与∠DOA之间的数量关系;
(3)若把图1中∠AOB绕点O转动到图2的位置,试说明(2)中∠BOC与∠DOA之间的数量关系还成立吗?
27.如图,点O在直线AB上,若∠AOD=150°,∠BOC=60°,求∠COD的度数.
28.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=19°,求∠AOB的度数.
29.如图,点A,O,B在同一条直线上,OD、OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=70°,求∠AOE的度数.
30.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=120°,求∠COD的度数.
31.如图所示,直线AE上有一点O,∠AOB=30°,∠BOC=∠AOB.
(1)求∠EOC的度数;
(2)如果OD平分∠EOC,求∠BOD的度数.
参考答案
1.解:由方向角的定义可知,
OA的方向是北偏东90°﹣30°=60°,因此选项A不符合题意;
OB的方向是北偏西90°﹣60°=30°,因此选项B不符合题意;
OC的方向是南偏西90°﹣15°=75°,因此选项C不符合题意;选项D符合题意;
故选:D.
2.解:由题意得:∠1=54°,∠2=15°,
∠3=90°﹣54°=36°,
∠AOB=36°+90°+15°=141°,
故选:C.
3.解:如图,
∵∠AOB=90°,
∴∠1+∠2=90°,
∴∠2=90°﹣∠1=90°﹣44°=46°,
∴OB的方向是南偏东46°,
故选:A.
4.解:由方向角的意义可知,∠NAB=60°,∠SAC=30°,
∴∠BOE=90°﹣60°=30°,
∴∠BAC=∠BAE+∠EAS+∠SAC
=30°+90°+30°
=150°,
故选:B.
5.解:设这个角的度数为x°,
依题意得(180﹣x)=x﹣30,
解得x=80,
90°﹣80°=10°.
答:这个角的余角为10°.
6.解:设这个角为x,
由题意得,180°﹣x=3(90°﹣x)﹣10°,
解得x=40°.
答:这个角的度数为40°.
7.解:设这个角是x°,
则(180﹣x)﹣3(90﹣x)=20,
解得x=55.
答:这个角的度数为55°.
8.解:设这个角是x,
则这个角的补角为180°﹣x,余角为90°﹣x,
所以3(90°﹣x)=180°﹣x,
整理,可得2x=90°,
解得:x=45°,
即这个角的度数为45°.
9.解:设这个角的度数为n°,由题意得:
3(90﹣n)+(180﹣n)=250,
解得:n=50.
经检验n=50符合题意,
答:这个角的度数为50°.
10.解:点M、N分别是AC、BC的中点,AC=12,BC=16,
MC=AC÷2=12÷2=6,
NC=CB÷2=16÷2=8,
由线段的和差,得
MN=MC+NC
=6+8
=14.
∴线段MN的长是14.
11.解:(1)∵AC=8cm,点M是AC的中点,
∴CM=AC=4cm,
∵BC=6cm,点N是BC的中点,
∴CN=BC=3cm,
∴MN=CM+CN=7cm,
∴线段MN的长度为7cm;
(2)∵点M、N分别是AC、BC的中点,
∴CM=AC,CN=BC,
∵AC=acm,BC=bcm,
∴MN=(AC+BC)=cm.
12.解:∵M、N分别为AC、AB的中点,
∴AC=2AM,AB=2AN,
∴AB﹣AC=2AN﹣2AM=2MN=16cm,
∵AC:CB=3:5,
∴AB=16÷(3+5﹣3)×(3+5)=25.6(cm).
故AB的长是25.6cm.
13.解:(1)∵点M是线段AC的中点,
∴AC=2AM,
∵AM=5cm,
∴AC=10cm,
∵AB=12cm,
∴BC=AB﹣AC=2cm;
(2)∵点M是线段AC的中点,点N是线段BC的中点,
∴BC=2NC,AC=2MC,
∵MN=NC+MC=8cm,
∴AB=BC+AC=2MN=2×8=16cm.
14.解:(1)∵N是BC的中点,M是AC的中点,AC=4,BC=6,
∴MC=2,CN=3,
∴MN=MC+CN=2+3=5;
(2)∵M是AC的中点,N是BC的中点,AB=m,
∴NM=MC+CN=AB=m.
故答案为:5.
15.解:∵M为线段AB的中点,AB=12,
∴AM=BM=AB=×12=6.
∵CM:CB=1:2,
∴CM=BM=×6=2.
∴AC=AM+CM=6+2=8.
16.解:∵点M为AB的中点,AB=12.
∴.
∵MC=2CB.
∴.
∴AC=AM+MC=10.
17.解:(1)根据题意画图如下:
(2)∵点D是AB的中点,
∴AD=AB,
∵AB=AC,
∴CD=5AD,
∵CD=6cm,
∴AD=cm,
∴AB=cm.
18.解:因为M是AC的中点,AC=6cm,
所以(cm).
因为AC=6cm,AB=21cm,
所以BC=AB﹣AC=15(cm),
因为CN:NB=1:2,
所以(cm),
所以MN=MC+CN=3+5=8(cm).
所以MN的长为8cm.
19.解:∵AB=3cm,BC=2AB,
∴BC=6(cm),
∴AC=AB+BC=9(cm),
∵AD:AC=4:3,
∴AD=9×=12(cm),
∴BD=AD+AB=15(cm),
∵点M是BD的中点,
∴BM=BD=(cm),
∴AM=BM﹣AB=﹣3=(cm).
20.解:设AB=x,则AM=x,AE=x,
根据题意得,x﹣x=2,
解得:x=28,
答:线段AB的长度为28cm.
21.解:(1)如图:
(2)∵AB=5,BC=3,
∴AC=8,
∵点O是线段AC的中点,
∴AO=CO=4,
∴BO=AB﹣AO=5﹣4=1,
∴OB长为1.
22.解:(1)2点15分时分针指向数字3,而时针从数字2开始转动的角度为15×0.5°=7.5°,
所以钟表上2时15分时,时针与分针所成的锐角的度数为30°﹣7.5°=22.5°;
(2)分针转过的角度为25×6°=150°.
23.解:(1)如图,∵由3点到3点45分,分针转了270°,时针转了270°×,
∴时针与分针的夹角是:180°﹣270°×=157.5°;
(2)设分针转的度数为x,则时针转的度数为,
得①90°+x﹣=100°,
解得,x=°,
°÷6°=(分);
②90°+﹣(x﹣180°)=100°,
解得,x=°,
°÷6°=(分);
∴9点过或分钟时,时针与分针成100°的角.
24.解:3点20分,时钟的分针与时针的夹角20×6﹣(3×30+0.5×20)=120﹣100=20°;
设过x分钟后它们的夹角为130°,得
6x+20﹣x=130,
解得x=20,
故过20分钟后它们的夹角为130°.
25.解:∵OE为∠BOD的平分线,∠BOE=17°,
∴∠BOD=2∠BOE=34°.
∴∠AOC=360°﹣∠AOB﹣∠COD﹣∠BOD=360°﹣90°﹣90°﹣34°=146°.
26.解:(1)∵∠BOC=2∠AOC,∠AOB=90°,
∴∠BOC+∠AOC=90°,
∵∠BOC=2∠AOC,
∴∠BOC=60°;
(2)∵∠COD=90°,
∴∠AOD=∠COD+∠AOC=90°+∠AOC,
∵∠AOB=90°,
∴∠BOC+∠AOC=90°,
∴∠BOC+∠AOD=∠BOC+90°+∠AOC=90°+90°=180°,
即∠BOC与∠AOD互为补角;
(3)成立.
∵∠AOB=∠COD=90°,
∴∠AOB+∠COD=180°,
∵∠BOC+∠AOD+∠AOB+∠COD=360°,
∴∠BOC+∠AOD=180°,
即∠BOC与∠AOD互为补角.
27.解:∵∠AOD=150°,∠BOC=60°,
∴∠COD=∠AOD+∠BOC﹣∠AOB=150°+60°﹣180°=30°.
28.解:设∠AOC=x,则∠COB=2x,
∴∠AOB=∠AOC+∠BOC=3x.
∵OD平分∠AOB,
∴∠AOD=∠AOB=.
∵∠COD=19°,
∴∠AOD﹣∠AOC=19°,
即=19.
解得:x=38.
∴∠AOB=3x=114°.
29.解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOC=∠AOC,∠COE=∠BOC,
∴∠DOE=∠DOC+∠COE=(∠AOC+∠BOC).
∵点A,O,B在同一条直线上,
∴∠AOC+∠BOC=180°.
∴∠DOE=×180°=90°.
(2))∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOC=∠AOC,∠COE=∠BOC,
∵∠COD=70°,
∴∠AOC=140°.
∴∠BOC=180°﹣∠AOC=40°.
∴∠COE=∠BOC=20°.
∴∠AOE=∠AOC+∠COE=140°+20°=160°.
30.解:∵OD平分∠AOB,∠AOB=120°,
∴∠AOD=∠AOB=×120°=60°,
∵∠BOC=2∠AOC,∠AOB=120°,
∴∠AOC=∠AOB=×120°=40°,
∴∠COD=∠AOD﹣∠AOC=60°﹣40°=20°.
31.解:(1)∵∠AOB=30°,∠BOC=∠AOB,
∴∠AOC=2∠AOB=60°,
∴∠EOC=120°.
(2)∵∠EOC=120°,OD平分∠EOC,
∴∠COD=∠EOC=60°,
∴∠BOD=∠COB+∠COD=30°+60°=90°.
