【寒假衔接】人教版八年级数学下册 18.1平行四边形 预习检测卷(word版、含答案)
文档属性
| 名称 | 【寒假衔接】人教版八年级数学下册 18.1平行四边形 预习检测卷(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 369.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 00:00:00 | ||
图片预览



文档简介
【寒假衔接】人教版 八年级数学下册
18.1平行四边形(预习检测卷)
一、选择题(共8题)
如图,将平行四边形 折叠,使顶点 落在 边上的点 处,折痕为 ,下列说法中不正确的是
A. B. C. D.
平行四边形有两个内角之和为 ,则该平行四边形的最大内角度数是
A. B. C. D.
如图,在平行四边形 中,两条对角线交于点 ,且 ,,.则下列选项错误的是
A.
B.
C.
D.平行四边形 的周长为
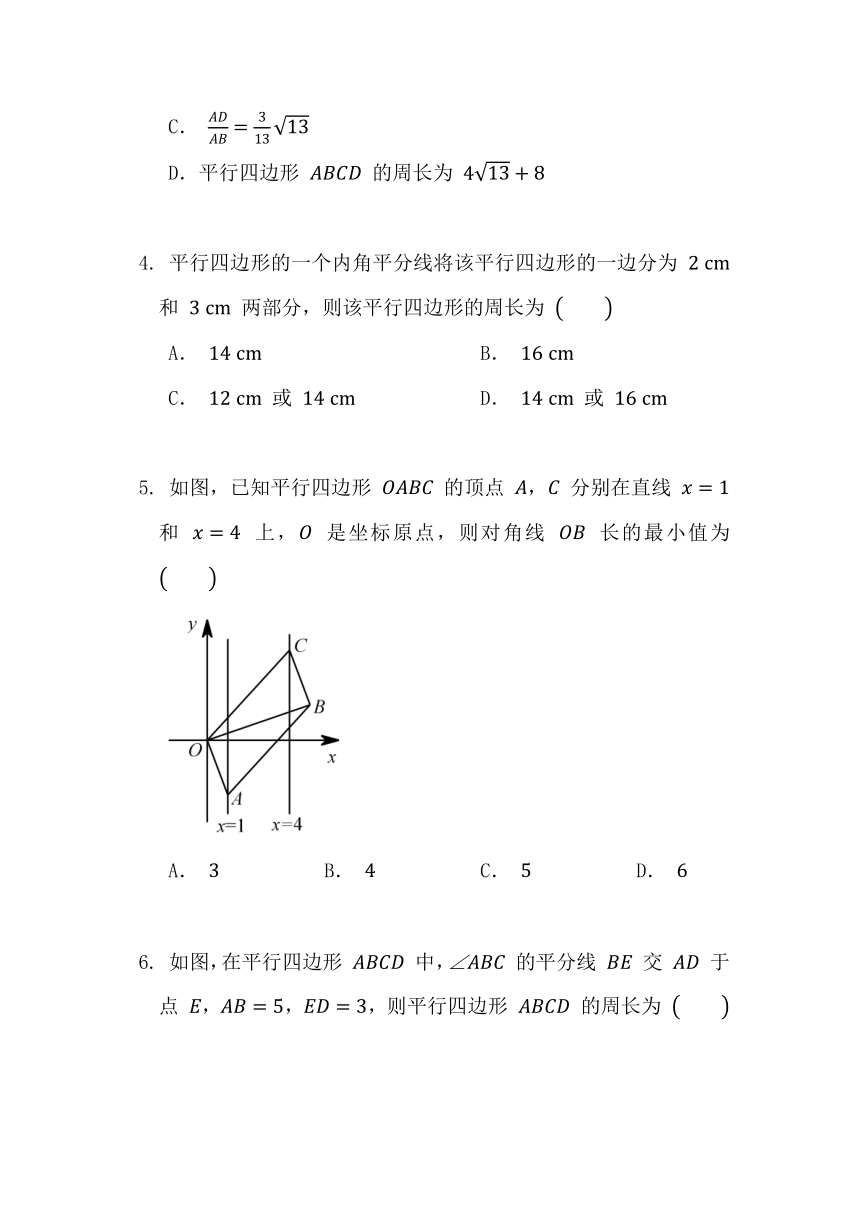
平行四边形的一个内角平分线将该平行四边形的一边分为 和 两部分,则该平行四边形的周长为
A. B.
C. 或 D. 或
如图,已知平行四边形 的顶点 , 分别在直线 和 上, 是坐标原点,则对角线 长的最小值为
A. B. C. D.
如图,在平行四边形 中, 的平分线 交 于点 ,,,则平行四边形 的周长为
A. B. C. D.
一个平行四边形的对角线的长分别为 和 ,则它的一边长可能为
A. B. C. D.
如图,若平行四边形 与平行四边形 关于 所在直线对称,,则 度数为
A. B. C. D.
二、填空题(共4题)
如图,长方形 中,,,点 是边 的中点,动点 从 点出发,以 的速度沿 运动,最终到达点 .若点 运动的时间为 ,那么当 时,以 ,, 为顶点的三角形的面积等于 .
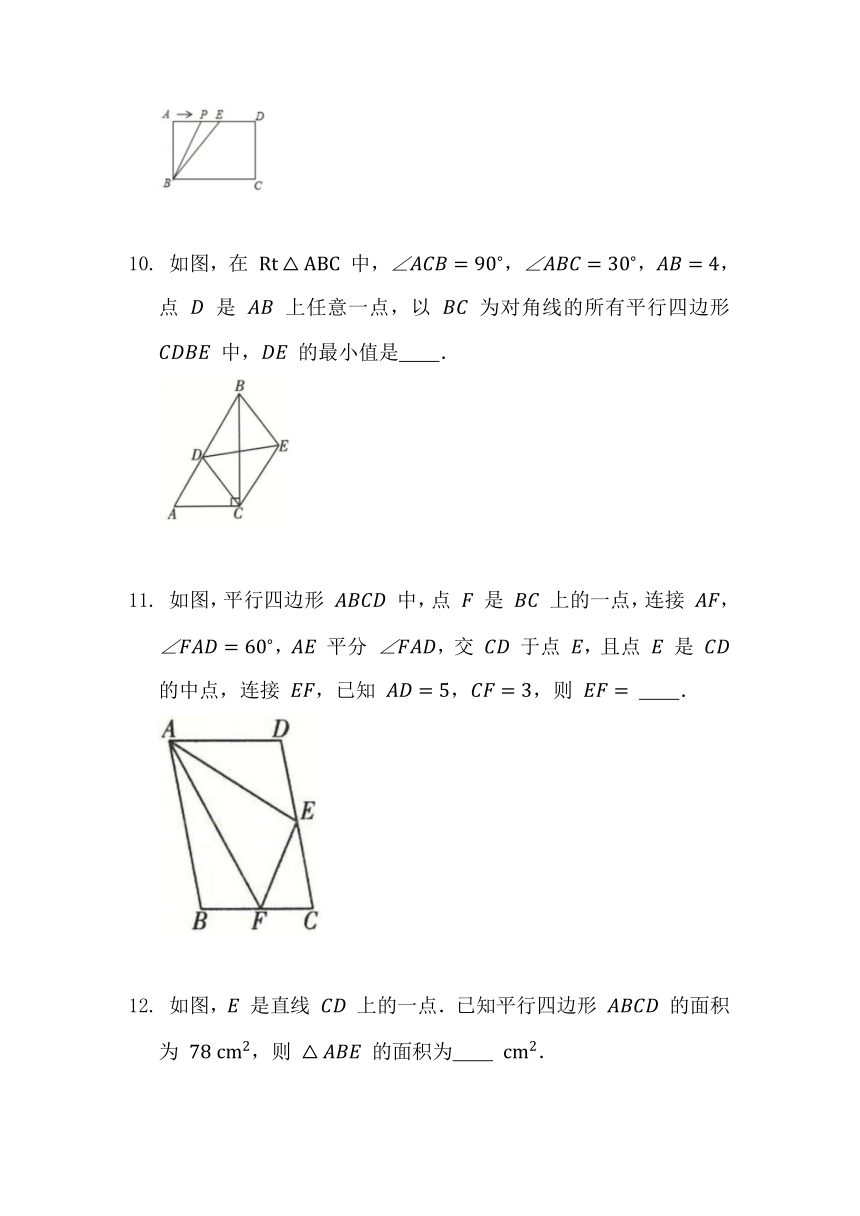
如图,在 中,,,,点 是 上任意一点,以 为对角线的所有平行四边形 中, 的最小值是 .
如图,平行四边形 中,点 是 上的一点,连接 ,, 平分 ,交 于点 ,且点 是 的中点,连接 ,已知 ,,则 .
如图, 是直线 上的一点.已知平行四边形 的面积为 ,则 的面积为 .
三、解答题(共3题)
如图,在平行四边形 中,对角线 , 相交于点 ,经过点 的直线交 于 ,交 于 .
(1) 求证:;
(2) 连接 ,,当 与 满足什么条件时,四边形 是矩形?请说明理由;
(3) 连接 ,,当 与 满足什么条件时,四边形 是菱形?请说明理由,
如图,已知在平行四边形 中,动点 在 边上,以每秒 的速度从点 向点 运动.
(1) 如图①,在运动过程中,若 平分 ,且满足 ,求 的度数;
(2) 如图②,在()的条件下,连接 并延长与 的延长线交于点 ,连接 ,若 ,求 的面积;
(3) 如图③,另一动点 在 边上,以每秒 的速度从点 出发,在 间往返运动,, 两点同时出发,当点 到达点 时停止运动(同时 点也停止),若 ,求当运动时间为多少秒时,以 ,,, 四点组成的四边形是平行四边形.
如图,已知四边形 为平行四边形,线段 垂直于对角线 ,连接 , 为 中点,连接 并延长至点 ,使 ,连接 .
(1) 猜想 与 的关系,并证明你的猜想;
(2) 求证:.
答案
一、选择题(共8题)
1. 【答案】D
【知识点】平行四边形及其性质
2. 【答案】D
【知识点】平行四边形及其性质
3. 【答案】C
【知识点】勾股定理、平行四边形及其性质
4. 【答案】D
【知识点】平行四边形及其性质
5. 【答案】C
【解析】过点 作 ,交直线 于点 ,过点 作 轴,交 轴于点 ,直线 与 交于点 ,与 轴交于点 ,直线 与 交于点 ,如图:
四边形 是平行四边形,
,,,
直线 与直线 均垂直于 轴,
,
四边形 是平行四边形,
,
,
,
,
在 和 中,
.
,
,
.
由于 的长不变,所以当 最小时(即 点在 轴上), 取得最小值,最小值为 .
【知识点】平行四边形的判定、平行四边形及其性质、平行四边形的概念、勾股定理
6. 【答案】C
【知识点】平行四边形及其性质
7. 【答案】C
【知识点】平行四边形及其性质
8. 【答案】A
【知识点】图形成轴对称、平行四边形及其性质
二、填空题(共4题)
9. 【答案】 或
【知识点】平行线间的距离
10. 【答案】
【知识点】勾股定理、平行四边形及其性质、30度所对的直角边等于斜边的一半
11. 【答案】
【知识点】平行四边形及其性质
12. 【答案】
【解析】分别过点 , 作直线 的垂线 ,,分别交直线 于点 ,,
所以 .
因为四边形 为平行四边形,
所以 ,
所以 ,
因为 ,
所以 .
【知识点】平行四边形及其性质
三、解答题(共3题)
13. 【答案】
(1) 四边形 是平行四边形,
,,
,,
在 和 中,
,
.
(2) 当 时,四边形 是矩形,
理由:
,
,
,
四边形 是平行四边形,
,
四边形 是矩形.
(3) 当 与 垂直时,四边形 是菱形,
理由:
,,
四边形 是平行四边形,
,
四边形 是菱形.
【知识点】对角线互相评分且相等的四边形、平行四边形及其性质
14. 【答案】
(1) 四边形 是平行四边形,
,
,
平分 ,
,
,
,
,
,
是等边三角形,
.
(2) 答图略,作 于 ,
则 ,
由勾股定理得,,
,
四边形 是平行四边形,
,,,
,
,
,
.
(3) 四边形 是平行四边形,
,
.
要使四边形 是平行四边形,则 ,
设运动时间为 秒,
①当 时,,,
,解得 ,不合題意,舍去;
②当 时,,,
,解得 ;
③当 时,,,
,解得 ;
④当 时,,,
,解得 .
综上所述,当运动时间为 秒或 秒或 秒时,以 ,,, 四点组成的四边形是平行四边形.
【知识点】平行四边形及其性质、一组对边平行且相等
15. 【答案】
(1) 猜想:,.
证明:答图略,连接 ,,.
,,
四边形 是平行四边形,
,,
四边形 是平行四边形,
,,
,,
四边形 是平行四边形,
,.
(2) 四边形 是平行四边形,
,
,
.
【知识点】两组对边分别相等、一组对边平行且相等、平行四边形及其性质
18.1平行四边形(预习检测卷)
一、选择题(共8题)
如图,将平行四边形 折叠,使顶点 落在 边上的点 处,折痕为 ,下列说法中不正确的是
A. B. C. D.
平行四边形有两个内角之和为 ,则该平行四边形的最大内角度数是
A. B. C. D.
如图,在平行四边形 中,两条对角线交于点 ,且 ,,.则下列选项错误的是
A.
B.
C.
D.平行四边形 的周长为
平行四边形的一个内角平分线将该平行四边形的一边分为 和 两部分,则该平行四边形的周长为
A. B.
C. 或 D. 或
如图,已知平行四边形 的顶点 , 分别在直线 和 上, 是坐标原点,则对角线 长的最小值为
A. B. C. D.
如图,在平行四边形 中, 的平分线 交 于点 ,,,则平行四边形 的周长为
A. B. C. D.
一个平行四边形的对角线的长分别为 和 ,则它的一边长可能为
A. B. C. D.
如图,若平行四边形 与平行四边形 关于 所在直线对称,,则 度数为
A. B. C. D.
二、填空题(共4题)
如图,长方形 中,,,点 是边 的中点,动点 从 点出发,以 的速度沿 运动,最终到达点 .若点 运动的时间为 ,那么当 时,以 ,, 为顶点的三角形的面积等于 .
如图,在 中,,,,点 是 上任意一点,以 为对角线的所有平行四边形 中, 的最小值是 .
如图,平行四边形 中,点 是 上的一点,连接 ,, 平分 ,交 于点 ,且点 是 的中点,连接 ,已知 ,,则 .
如图, 是直线 上的一点.已知平行四边形 的面积为 ,则 的面积为 .
三、解答题(共3题)
如图,在平行四边形 中,对角线 , 相交于点 ,经过点 的直线交 于 ,交 于 .
(1) 求证:;
(2) 连接 ,,当 与 满足什么条件时,四边形 是矩形?请说明理由;
(3) 连接 ,,当 与 满足什么条件时,四边形 是菱形?请说明理由,
如图,已知在平行四边形 中,动点 在 边上,以每秒 的速度从点 向点 运动.
(1) 如图①,在运动过程中,若 平分 ,且满足 ,求 的度数;
(2) 如图②,在()的条件下,连接 并延长与 的延长线交于点 ,连接 ,若 ,求 的面积;
(3) 如图③,另一动点 在 边上,以每秒 的速度从点 出发,在 间往返运动,, 两点同时出发,当点 到达点 时停止运动(同时 点也停止),若 ,求当运动时间为多少秒时,以 ,,, 四点组成的四边形是平行四边形.
如图,已知四边形 为平行四边形,线段 垂直于对角线 ,连接 , 为 中点,连接 并延长至点 ,使 ,连接 .
(1) 猜想 与 的关系,并证明你的猜想;
(2) 求证:.
答案
一、选择题(共8题)
1. 【答案】D
【知识点】平行四边形及其性质
2. 【答案】D
【知识点】平行四边形及其性质
3. 【答案】C
【知识点】勾股定理、平行四边形及其性质
4. 【答案】D
【知识点】平行四边形及其性质
5. 【答案】C
【解析】过点 作 ,交直线 于点 ,过点 作 轴,交 轴于点 ,直线 与 交于点 ,与 轴交于点 ,直线 与 交于点 ,如图:
四边形 是平行四边形,
,,,
直线 与直线 均垂直于 轴,
,
四边形 是平行四边形,
,
,
,
,
在 和 中,
.
,
,
.
由于 的长不变,所以当 最小时(即 点在 轴上), 取得最小值,最小值为 .
【知识点】平行四边形的判定、平行四边形及其性质、平行四边形的概念、勾股定理
6. 【答案】C
【知识点】平行四边形及其性质
7. 【答案】C
【知识点】平行四边形及其性质
8. 【答案】A
【知识点】图形成轴对称、平行四边形及其性质
二、填空题(共4题)
9. 【答案】 或
【知识点】平行线间的距离
10. 【答案】
【知识点】勾股定理、平行四边形及其性质、30度所对的直角边等于斜边的一半
11. 【答案】
【知识点】平行四边形及其性质
12. 【答案】
【解析】分别过点 , 作直线 的垂线 ,,分别交直线 于点 ,,
所以 .
因为四边形 为平行四边形,
所以 ,
所以 ,
因为 ,
所以 .
【知识点】平行四边形及其性质
三、解答题(共3题)
13. 【答案】
(1) 四边形 是平行四边形,
,,
,,
在 和 中,
,
.
(2) 当 时,四边形 是矩形,
理由:
,
,
,
四边形 是平行四边形,
,
四边形 是矩形.
(3) 当 与 垂直时,四边形 是菱形,
理由:
,,
四边形 是平行四边形,
,
四边形 是菱形.
【知识点】对角线互相评分且相等的四边形、平行四边形及其性质
14. 【答案】
(1) 四边形 是平行四边形,
,
,
平分 ,
,
,
,
,
,
是等边三角形,
.
(2) 答图略,作 于 ,
则 ,
由勾股定理得,,
,
四边形 是平行四边形,
,,,
,
,
,
.
(3) 四边形 是平行四边形,
,
.
要使四边形 是平行四边形,则 ,
设运动时间为 秒,
①当 时,,,
,解得 ,不合題意,舍去;
②当 时,,,
,解得 ;
③当 时,,,
,解得 ;
④当 时,,,
,解得 .
综上所述,当运动时间为 秒或 秒或 秒时,以 ,,, 四点组成的四边形是平行四边形.
【知识点】平行四边形及其性质、一组对边平行且相等
15. 【答案】
(1) 猜想:,.
证明:答图略,连接 ,,.
,,
四边形 是平行四边形,
,,
四边形 是平行四边形,
,,
,,
四边形 是平行四边形,
,.
(2) 四边形 是平行四边形,
,
,
.
【知识点】两组对边分别相等、一组对边平行且相等、平行四边形及其性质
