【寒假衔接】人教版 八年级数学下册 19.3课题学习 选择方案 预习检测卷(word版、含答案)
文档属性
| 名称 | 【寒假衔接】人教版 八年级数学下册 19.3课题学习 选择方案 预习检测卷(word版、含答案) | 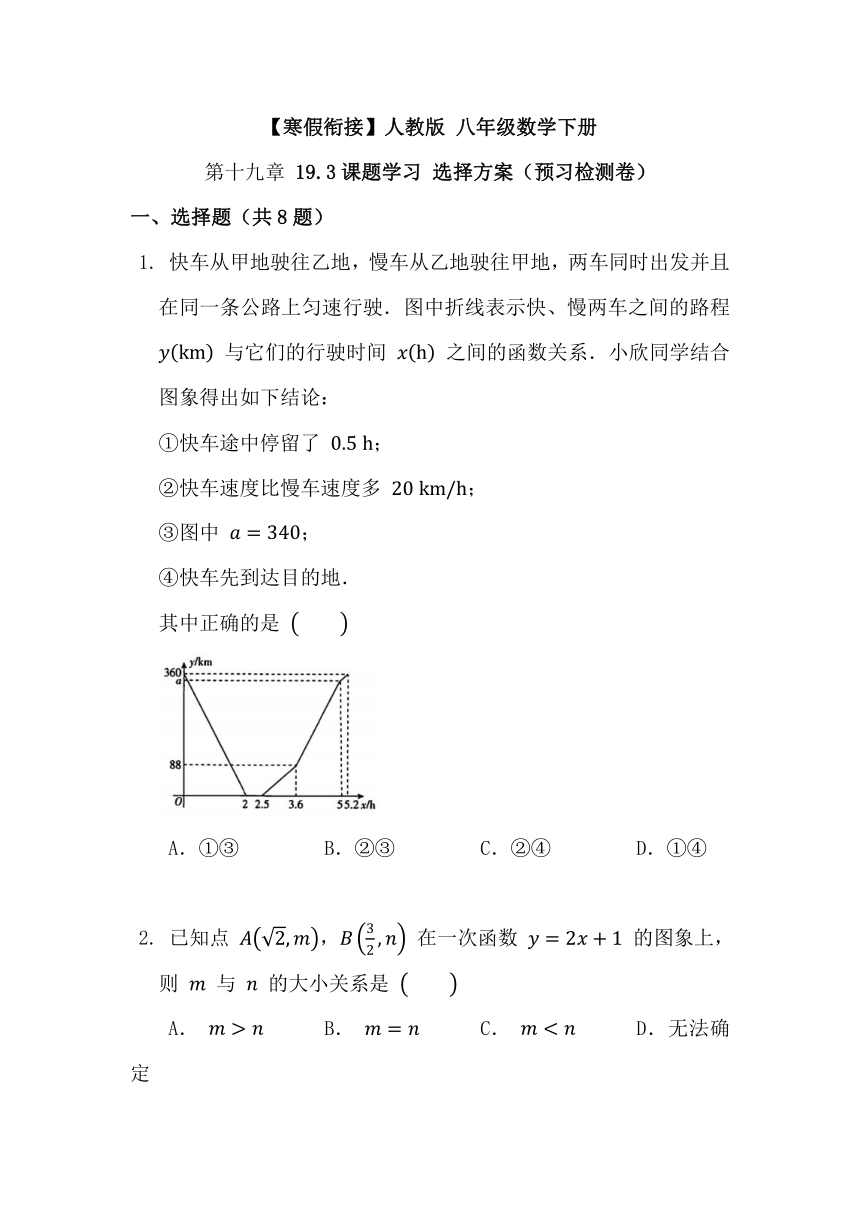 | |
| 格式 | docx | ||
| 文件大小 | 108.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 21:26:46 | ||
图片预览





文档简介
【寒假衔接】人教版 八年级数学下册
19.3课题学习 选择方案(预习检测卷)
一、选择题(共8题)
快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图象得出如下结论:
①快车途中停留了 ;
②快车速度比慢车速度多 ;
③图中 ;
④快车先到达目的地.
其中正确的是
A.①③ B.②③ C.②④ D.①④
已知点 , 在一次函数 的图象上,则 与 的大小关系是
A. B. C. D.无法确定
函数 中自变量 的取值范围是
A. B. C. D.
某通信公司提供了两种移动电话收费方式:方式 ,收月基本费 元,再以每分钟 元的价格按通话时间计费;方式 ,收月基本费 元,送 分钟通话时间,超过 分钟的部分,以每分钟 元的价格计费.给出下列结论:①如图描述的是方式 的收费方法;②若月通话时间少于 分钟,则选择方式 省钱;③若月通信费为 元,则方式 比方式 的通话时间多;④若方式 比方式 的通信费多 元,则方式 比方式 的通话时间多 分钟.其中正确的是
A.①② B.③④ C.①②③ D.①②③④
如图,直线 反映了某公司产品的销售收入 (元)与销售量 (吨)之间的关系,直线 反映了该公司产品的销售成本 (元)与销售量 (吨)之间的关系.若该公司已经盈利(收入大于成本),则销售量
A.小于 吨 B.大于 吨 C.小于 吨 D.大于 吨
某品牌鞋子的长度 与鞋子的码数 之间满足一次函数关系.若 码鞋子的长度为 , 码鞋子的长度为 ,则 码鞋子的长度为
A. B. C. D.
某地电话拨号上网有两种收费方式:计时制——每分钟 元,包月制——每月 元.此外,每一种上网方式都得加收通信费每分钟 元,某用户估计一个月的上网时间为 ,则采用哪种收费方式较为合算
A.计时制 B.包月制 C.两种一样 D.不确定
甲、乙两家工厂出示的招工就业标准如下:甲工厂年薪酬 元,每满一年加工龄工资 元;乙工厂每半年薪酬为 元,每满半年加工龄工资 元.若你是应聘者,你会选择
A.甲工厂 B.乙工厂
C.甲工厂或乙工厂 D.无法选择
二、填空题(共5题)
利用函数值的大小选择方案主要有两步:将实际问题数量化,根据实际问题建立数学模型,列出相关变量的两个函数解析式;根据题意,将两个函数解析式转化为 或 后再求解.
在某一问题中,符合条件的方案有多种,要求从中选出最优方案,解答的关键是学会运用 观点去分析、概括实际问题中的信息,将其转化为数学模型,综合 的知识求解.
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡.使用这两种卡租书,租书金额 (元)与租书时间 (天)之间的关系如图所示,当租书时间为 天时,应使用 比较合算.
某校计划购买篮球和排球共 个,已知篮球每个 元,排球每个 元.设购买篮球 个,购买篮球和排球的总费用为 元,则 与 之间的函数关系式为 .如果要求篮球的个数不少于排球个数的 倍,则篮球购买 个、排球购买 个才能使总费用最少.
掌握用一次函数解决实际问题的步骤
()分析变量之间的关系,建立 关系式;
()求出自变量的 ;
()应用一次函数的 解决实际问题.
三、解答题(共4题)
把一个长 ,宽 的长方形的宽增加 ,长不变,长方形的面积 随 的变化而变化.
(1) 求 与 的函数解析式;
(2) 若增加宽度后的长方形面积为 ,求 的值.
小美打算买一束百合和康乃馨组合的鲜花,在“母亲节”送给妈妈.已知买 枝百合和 枝康乃馨共需花费 元, 枝康乃馨的价格比 枝百合的价格贵 元.
(1) 买一枝康乃馨和一枝百合各需多少元?
(2) 小美准备买康乃馨和百合共 枝,且百合不少于 枝.设买这束鲜花所需费用为 元,康乃馨有 枝,求 与 之间的函数解析式,并设计一种使费用最少的买花方案,写出最少费用.
甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为 元/千克,如果一次购买 千克以上的苹果,超过 千克的部分按标价 折售卖:用 (千克)表示购买苹果的质量,(元)表示付款金额,
(1) 文文购买 千克苹果需付款 元;购买 千克苹果需付款 元.
(2) 求付款金额 (元)关于购买苹果的质量 (千克)的函数解析式.
(3) 当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为 元/千克,且全部按标价的 折售卖.文文要购买 千克苹果,她在哪个超市购买更划算?
某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费 (元)是行李质量 的一次函数.已知行李质量为 时需付行李费 元,行李质量为 时需付行李费 元.
(1) 当行李的质量 超过规定时,求 与 之间的函数表达式;
(2) 求旅客最多可免费携带行李的质量.
答案
一、选择题(共8题)
1. 【答案】B
【解析】根据题意可知,两车的速度和为 .
相遇后慢车停留了 ,
快车停留了 ,故①结论错误.
慢车的速度为 ,
则快车的速度为 ,
所以快车速度比慢车速度多 ,故②结论正确.
,
所以图中 ,故③结论正确.
快车到达终点的时间为 ,
慢车到达终点的时间为 .
因为 ,
所以慢车先到达目的地,故④结论错误.
所以正确的是②③.
【知识点】用函数图象表示实际问题中的函数关系
2. 【答案】C
【解析】 点 , 在一次函数 的图象上,
,,
,
.
【知识点】k,b对一次函数图象及性质的影响
3. 【答案】A
【解析】由题意得
.
【知识点】分式与二次根式综合型自变量的取值范围
4. 【答案】C
【知识点】方案问题
5. 【答案】D
【知识点】方案问题
6. 【答案】B
【知识点】一次函数的应用
7. 【答案】B
【知识点】方案问题
8. 【答案】B
【知识点】简单的代数式求值、简单列代数式
二、填空题(共5题)
9. 【答案】一元一次方程;一元一次不等式
【知识点】方案问题
10. 【答案】函数;不等式、方程
【知识点】方案决策
11. 【答案】会员卡
【知识点】方案问题
12. 【答案】 ; ;
【知识点】方案问题
13. 【答案】一次函数;取值范围;图象和性质
【知识点】方案问题
三、解答题(共4题)
14. 【答案】
(1) ;
(2) 依题意,得 ,即 ,解得 .
【知识点】一次函数的应用
15. 【答案】
(1) 设买一枝康乃馨需 元,买一枝百合需 元.根据题意,得解得 买一枝康乃馨需 元,买一枝百合需 元.
(2) 根据题意,得 ,
百合不少于 枝,
,
解得 .
,
随 的增大而减小.
当 时, 取得最小值 .
买 枝康乃馨,买 (枝)百合费用最少,最少费用是 元.
【知识点】综合应用、方案问题
16. 【答案】
(1) ;
(2) 由题意,当 时,;
当 时,.
付款金额 (元)关于购买苹果的质量 (千克)的函数解析式为 .
(3) 文文在甲超市购买 千克苹果需付 (元).
文文在乙超市购买 千克苹果需付 (元).
,
文文在甲超市购买更划算.
【知识点】方案问题
17. 【答案】
(1) 根据题意,设 与 的函数表达式为 .
当 时,,得 .
当 时,,得 .
解方程组 得
所求函数表达式为 .
(2) 当 时,,得 .
答:旅客最多可免费携带行李 .
【知识点】一次函数的应用
19.3课题学习 选择方案(预习检测卷)
一、选择题(共8题)
快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图象得出如下结论:
①快车途中停留了 ;
②快车速度比慢车速度多 ;
③图中 ;
④快车先到达目的地.
其中正确的是
A.①③ B.②③ C.②④ D.①④
已知点 , 在一次函数 的图象上,则 与 的大小关系是
A. B. C. D.无法确定
函数 中自变量 的取值范围是
A. B. C. D.
某通信公司提供了两种移动电话收费方式:方式 ,收月基本费 元,再以每分钟 元的价格按通话时间计费;方式 ,收月基本费 元,送 分钟通话时间,超过 分钟的部分,以每分钟 元的价格计费.给出下列结论:①如图描述的是方式 的收费方法;②若月通话时间少于 分钟,则选择方式 省钱;③若月通信费为 元,则方式 比方式 的通话时间多;④若方式 比方式 的通信费多 元,则方式 比方式 的通话时间多 分钟.其中正确的是
A.①② B.③④ C.①②③ D.①②③④
如图,直线 反映了某公司产品的销售收入 (元)与销售量 (吨)之间的关系,直线 反映了该公司产品的销售成本 (元)与销售量 (吨)之间的关系.若该公司已经盈利(收入大于成本),则销售量
A.小于 吨 B.大于 吨 C.小于 吨 D.大于 吨
某品牌鞋子的长度 与鞋子的码数 之间满足一次函数关系.若 码鞋子的长度为 , 码鞋子的长度为 ,则 码鞋子的长度为
A. B. C. D.
某地电话拨号上网有两种收费方式:计时制——每分钟 元,包月制——每月 元.此外,每一种上网方式都得加收通信费每分钟 元,某用户估计一个月的上网时间为 ,则采用哪种收费方式较为合算
A.计时制 B.包月制 C.两种一样 D.不确定
甲、乙两家工厂出示的招工就业标准如下:甲工厂年薪酬 元,每满一年加工龄工资 元;乙工厂每半年薪酬为 元,每满半年加工龄工资 元.若你是应聘者,你会选择
A.甲工厂 B.乙工厂
C.甲工厂或乙工厂 D.无法选择
二、填空题(共5题)
利用函数值的大小选择方案主要有两步:将实际问题数量化,根据实际问题建立数学模型,列出相关变量的两个函数解析式;根据题意,将两个函数解析式转化为 或 后再求解.
在某一问题中,符合条件的方案有多种,要求从中选出最优方案,解答的关键是学会运用 观点去分析、概括实际问题中的信息,将其转化为数学模型,综合 的知识求解.
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡.使用这两种卡租书,租书金额 (元)与租书时间 (天)之间的关系如图所示,当租书时间为 天时,应使用 比较合算.
某校计划购买篮球和排球共 个,已知篮球每个 元,排球每个 元.设购买篮球 个,购买篮球和排球的总费用为 元,则 与 之间的函数关系式为 .如果要求篮球的个数不少于排球个数的 倍,则篮球购买 个、排球购买 个才能使总费用最少.
掌握用一次函数解决实际问题的步骤
()分析变量之间的关系,建立 关系式;
()求出自变量的 ;
()应用一次函数的 解决实际问题.
三、解答题(共4题)
把一个长 ,宽 的长方形的宽增加 ,长不变,长方形的面积 随 的变化而变化.
(1) 求 与 的函数解析式;
(2) 若增加宽度后的长方形面积为 ,求 的值.
小美打算买一束百合和康乃馨组合的鲜花,在“母亲节”送给妈妈.已知买 枝百合和 枝康乃馨共需花费 元, 枝康乃馨的价格比 枝百合的价格贵 元.
(1) 买一枝康乃馨和一枝百合各需多少元?
(2) 小美准备买康乃馨和百合共 枝,且百合不少于 枝.设买这束鲜花所需费用为 元,康乃馨有 枝,求 与 之间的函数解析式,并设计一种使费用最少的买花方案,写出最少费用.
甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为 元/千克,如果一次购买 千克以上的苹果,超过 千克的部分按标价 折售卖:用 (千克)表示购买苹果的质量,(元)表示付款金额,
(1) 文文购买 千克苹果需付款 元;购买 千克苹果需付款 元.
(2) 求付款金额 (元)关于购买苹果的质量 (千克)的函数解析式.
(3) 当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为 元/千克,且全部按标价的 折售卖.文文要购买 千克苹果,她在哪个超市购买更划算?
某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费 (元)是行李质量 的一次函数.已知行李质量为 时需付行李费 元,行李质量为 时需付行李费 元.
(1) 当行李的质量 超过规定时,求 与 之间的函数表达式;
(2) 求旅客最多可免费携带行李的质量.
答案
一、选择题(共8题)
1. 【答案】B
【解析】根据题意可知,两车的速度和为 .
相遇后慢车停留了 ,
快车停留了 ,故①结论错误.
慢车的速度为 ,
则快车的速度为 ,
所以快车速度比慢车速度多 ,故②结论正确.
,
所以图中 ,故③结论正确.
快车到达终点的时间为 ,
慢车到达终点的时间为 .
因为 ,
所以慢车先到达目的地,故④结论错误.
所以正确的是②③.
【知识点】用函数图象表示实际问题中的函数关系
2. 【答案】C
【解析】 点 , 在一次函数 的图象上,
,,
,
.
【知识点】k,b对一次函数图象及性质的影响
3. 【答案】A
【解析】由题意得
.
【知识点】分式与二次根式综合型自变量的取值范围
4. 【答案】C
【知识点】方案问题
5. 【答案】D
【知识点】方案问题
6. 【答案】B
【知识点】一次函数的应用
7. 【答案】B
【知识点】方案问题
8. 【答案】B
【知识点】简单的代数式求值、简单列代数式
二、填空题(共5题)
9. 【答案】一元一次方程;一元一次不等式
【知识点】方案问题
10. 【答案】函数;不等式、方程
【知识点】方案决策
11. 【答案】会员卡
【知识点】方案问题
12. 【答案】 ; ;
【知识点】方案问题
13. 【答案】一次函数;取值范围;图象和性质
【知识点】方案问题
三、解答题(共4题)
14. 【答案】
(1) ;
(2) 依题意,得 ,即 ,解得 .
【知识点】一次函数的应用
15. 【答案】
(1) 设买一枝康乃馨需 元,买一枝百合需 元.根据题意,得解得 买一枝康乃馨需 元,买一枝百合需 元.
(2) 根据题意,得 ,
百合不少于 枝,
,
解得 .
,
随 的增大而减小.
当 时, 取得最小值 .
买 枝康乃馨,买 (枝)百合费用最少,最少费用是 元.
【知识点】综合应用、方案问题
16. 【答案】
(1) ;
(2) 由题意,当 时,;
当 时,.
付款金额 (元)关于购买苹果的质量 (千克)的函数解析式为 .
(3) 文文在甲超市购买 千克苹果需付 (元).
文文在乙超市购买 千克苹果需付 (元).
,
文文在甲超市购买更划算.
【知识点】方案问题
17. 【答案】
(1) 根据题意,设 与 的函数表达式为 .
当 时,,得 .
当 时,,得 .
解方程组 得
所求函数表达式为 .
(2) 当 时,,得 .
答:旅客最多可免费携带行李 .
【知识点】一次函数的应用
