【寒假衔接】人教版 八年级数学下册 19.1函数 预习检测卷(word版、含答案)
文档属性
| 名称 | 【寒假衔接】人教版 八年级数学下册 19.1函数 预习检测卷(word版、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 228.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 00:00:00 | ||
图片预览




文档简介
【寒假衔接】人教版 八年级数学下册
19.1一次函数(预习检测卷)
一、选择题(共8题)
如图,大小两个正方形在同一水平线上,小正方形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为 ,大小正方形重叠部分的面积为 ,则下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
设圆的面积为 ,直径为 ,则对于等式 ,下列说法正确的是
A. 是 的函数 B. 是 的函数
C. 是 的函数 D. 不是 的函数
【测试 】圆周长公式 中,下列说法正确的是
A. , 是变量, 为常量 B. , 为变量,, 为常量
C. 为变量,,, 为常量 D. 为变量,,, 为常量
假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A. 个 B. 个 C. 个 D. 个
在 中,它的底边是 ,底边上的高是 ,则三角形的面积 ,当 为定长时,此式中
A. , 是变量,, 是常量 B. ,, 是变量, 是常量
C. 是变量, 是常量 D. 是变量,,, 是常量
年春节期间,许多在西安市的外地员工都晌应政府号召留在西安过春节.滞留在西安的小豪给远在北京的妻儿打电话,电话费随着通话时间的变化而变化,在这个过程中,自变量和因变量分别是
A.小豪和妻儿 B.小豪和电话费
C.电话费和通话时间 D.通话时间和电话费
小王从北京给远在上海的爷爷打电话,电话费随着时间的变化而变化,在这个问题中,变量是
A.小王、爷爷 B.电话费、时间 C.时间 D.爷爷
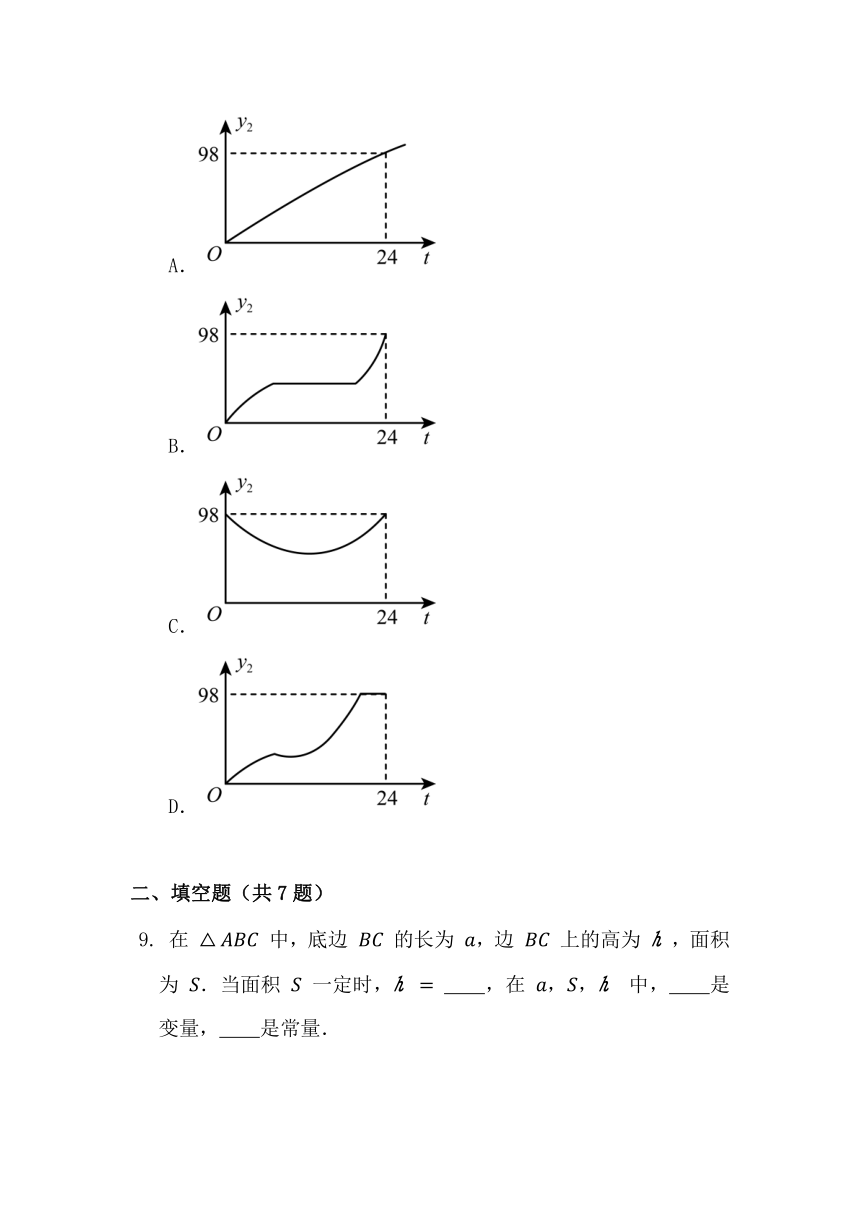
随着时代的进步,人们对 (空气中直径小于或等于 微米的颗粒)的关注日益密切.某市一天中 的值 随时间 的变化如图所示,设 表示 时到 时 的值的极差(即 时到 时 的最大值与最小值的差),则 与 的函数关系大致是
A.
B.
C.
D.
二、填空题(共7题)
在 中,底边 的长为 ,边 上的高为 ,面积为 .当面积 一定时, ,在 ,, 中, 是变量, 是常量.
已知函数 ,当 时, 的值是 .
在一个变化过程中,我们称数值发生变化的量为 ,数值始终不变的量为 .
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横,纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的 .
已知 ,那么当 时, .
若圆柱的底面半径 不变,圆柱的体积 与圆柱的高 的关系式为 ,则常量是 ,变量是 .
骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一关系中,因变量是 .
三、解答题(共3题)
设有三个变量 ,,,其中 是 的正比例函数, 是 的正比例函数.
(1) 求证: 是 的正比例函数;
(2) 如果 时,,求出 关于 的函数关系式.
点燃蜡烛时,蜡烛燃烧长度与时间成正比例函数关系,长为 的蜡烛点燃 后变短了 .设蜡烛点燃 后变短了 .求:
(1) 用 表示 的解析式;
(2) 自变量 的取值范围;
(3) 此蜡烛几分钟后燃烧完?
小明骑单车上学,当他骑了一段时,想起要买本书,于是又返回到刚经过的新华书店,买到书后继续去学校,以下是他离家距离与所用时间的关系示意图.根据图中提供的信息回答下列问题:
(1) 小明家到学校的距离是 ,小明在书店停留了 ;
(2) 本次上学途中,小明一共行驶了 ,一共用了 ;
(3) 若骑单车的速度超过 就超越了安全限度,问:在整个上学的途中,哪个时间段小明骑车速度最快?速度在安全限度内吗?
答案
一、选择题(共8题)
1. 【答案】C
【解析】依题意,阴影部分的面积函数关系式是分段函数,面积由“增加 不变 减少”变化.
【知识点】用函数图象表示实际问题中的函数关系
2. 【答案】C
【知识点】函数的概念
3. 【答案】B
【解析】在圆周长公式 中,, 是常量,, 是变量.
故选:B.
【知识点】常量、变量
4. 【答案】C
【知识点】常量、变量
5. 【答案】A
【知识点】变量、常量
6. 【答案】D
【解析】 电话费随着通话时间的变化而变化,
自变量是通话时间,因变量是电话费.
【知识点】变量
7. 【答案】B
【知识点】变量
8. 【答案】B
【解析】当 时,极差 ,
当 时,极差 随 的增大而增大,
当 时,极差 随 的增大保持 不变,
当 时,极差 随 的增大而增大,最大值为 .
【知识点】极差、用函数图象表示实际问题中的函数关系
二、填空题(共7题)
9. 【答案】 ; , ;
【知识点】常量、变量
10. 【答案】
【知识点】自变量与函数值
11. 【答案】变量;常量
【知识点】常量、变量
12. 【答案】图象
【知识点】图像法
13. 【答案】
【解析】当 时,.
【知识点】自变量与函数值
14. 【答案】 , ; ,
【知识点】变量、常量
15. 【答案】骆驼的体温
【知识点】变量
三、解答题(共3题)
16. 【答案】
(1) 设 ,,则有 ,,故 是 的正比例函数.
(2) 将 , 代入 ,得 ,解得 ,则 .
【知识点】正比例函数的定义、解析式法
17. 【答案】
(1) 依题意可知蜡烛燃烧变短的长度 与燃烧时间 是正比例函数关系,故可设 .
当 时,,
,解得 ,
函数的解析式为 .
(2) ,
,
自变量 的取值范围是 .
(3) 当 时,即 ,解得 ,
此蜡烛 后燃烧完.
【知识点】正比例函数的定义、实际问题中的自变量的取值范围、解析式法
18. 【答案】
(1) ;
(2) ;
(3) 由图象可知: 时,平均速度 ;
时,平均速度 ;
时,平均速度 ,
时速度最快,不在安全限度内.
【解析】
(2) 行驶的总路程为:,共用了 .
【知识点】用函数图象表示实际问题中的函数关系
19.1一次函数(预习检测卷)
一、选择题(共8题)
如图,大小两个正方形在同一水平线上,小正方形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为 ,大小正方形重叠部分的面积为 ,则下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
设圆的面积为 ,直径为 ,则对于等式 ,下列说法正确的是
A. 是 的函数 B. 是 的函数
C. 是 的函数 D. 不是 的函数
【测试 】圆周长公式 中,下列说法正确的是
A. , 是变量, 为常量 B. , 为变量,, 为常量
C. 为变量,,, 为常量 D. 为变量,,, 为常量
假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A. 个 B. 个 C. 个 D. 个
在 中,它的底边是 ,底边上的高是 ,则三角形的面积 ,当 为定长时,此式中
A. , 是变量,, 是常量 B. ,, 是变量, 是常量
C. 是变量, 是常量 D. 是变量,,, 是常量
年春节期间,许多在西安市的外地员工都晌应政府号召留在西安过春节.滞留在西安的小豪给远在北京的妻儿打电话,电话费随着通话时间的变化而变化,在这个过程中,自变量和因变量分别是
A.小豪和妻儿 B.小豪和电话费
C.电话费和通话时间 D.通话时间和电话费
小王从北京给远在上海的爷爷打电话,电话费随着时间的变化而变化,在这个问题中,变量是
A.小王、爷爷 B.电话费、时间 C.时间 D.爷爷
随着时代的进步,人们对 (空气中直径小于或等于 微米的颗粒)的关注日益密切.某市一天中 的值 随时间 的变化如图所示,设 表示 时到 时 的值的极差(即 时到 时 的最大值与最小值的差),则 与 的函数关系大致是
A.
B.
C.
D.
二、填空题(共7题)
在 中,底边 的长为 ,边 上的高为 ,面积为 .当面积 一定时, ,在 ,, 中, 是变量, 是常量.
已知函数 ,当 时, 的值是 .
在一个变化过程中,我们称数值发生变化的量为 ,数值始终不变的量为 .
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横,纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的 .
已知 ,那么当 时, .
若圆柱的底面半径 不变,圆柱的体积 与圆柱的高 的关系式为 ,则常量是 ,变量是 .
骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一关系中,因变量是 .
三、解答题(共3题)
设有三个变量 ,,,其中 是 的正比例函数, 是 的正比例函数.
(1) 求证: 是 的正比例函数;
(2) 如果 时,,求出 关于 的函数关系式.
点燃蜡烛时,蜡烛燃烧长度与时间成正比例函数关系,长为 的蜡烛点燃 后变短了 .设蜡烛点燃 后变短了 .求:
(1) 用 表示 的解析式;
(2) 自变量 的取值范围;
(3) 此蜡烛几分钟后燃烧完?
小明骑单车上学,当他骑了一段时,想起要买本书,于是又返回到刚经过的新华书店,买到书后继续去学校,以下是他离家距离与所用时间的关系示意图.根据图中提供的信息回答下列问题:
(1) 小明家到学校的距离是 ,小明在书店停留了 ;
(2) 本次上学途中,小明一共行驶了 ,一共用了 ;
(3) 若骑单车的速度超过 就超越了安全限度,问:在整个上学的途中,哪个时间段小明骑车速度最快?速度在安全限度内吗?
答案
一、选择题(共8题)
1. 【答案】C
【解析】依题意,阴影部分的面积函数关系式是分段函数,面积由“增加 不变 减少”变化.
【知识点】用函数图象表示实际问题中的函数关系
2. 【答案】C
【知识点】函数的概念
3. 【答案】B
【解析】在圆周长公式 中,, 是常量,, 是变量.
故选:B.
【知识点】常量、变量
4. 【答案】C
【知识点】常量、变量
5. 【答案】A
【知识点】变量、常量
6. 【答案】D
【解析】 电话费随着通话时间的变化而变化,
自变量是通话时间,因变量是电话费.
【知识点】变量
7. 【答案】B
【知识点】变量
8. 【答案】B
【解析】当 时,极差 ,
当 时,极差 随 的增大而增大,
当 时,极差 随 的增大保持 不变,
当 时,极差 随 的增大而增大,最大值为 .
【知识点】极差、用函数图象表示实际问题中的函数关系
二、填空题(共7题)
9. 【答案】 ; , ;
【知识点】常量、变量
10. 【答案】
【知识点】自变量与函数值
11. 【答案】变量;常量
【知识点】常量、变量
12. 【答案】图象
【知识点】图像法
13. 【答案】
【解析】当 时,.
【知识点】自变量与函数值
14. 【答案】 , ; ,
【知识点】变量、常量
15. 【答案】骆驼的体温
【知识点】变量
三、解答题(共3题)
16. 【答案】
(1) 设 ,,则有 ,,故 是 的正比例函数.
(2) 将 , 代入 ,得 ,解得 ,则 .
【知识点】正比例函数的定义、解析式法
17. 【答案】
(1) 依题意可知蜡烛燃烧变短的长度 与燃烧时间 是正比例函数关系,故可设 .
当 时,,
,解得 ,
函数的解析式为 .
(2) ,
,
自变量 的取值范围是 .
(3) 当 时,即 ,解得 ,
此蜡烛 后燃烧完.
【知识点】正比例函数的定义、实际问题中的自变量的取值范围、解析式法
18. 【答案】
(1) ;
(2) ;
(3) 由图象可知: 时,平均速度 ;
时,平均速度 ;
时,平均速度 ,
时速度最快,不在安全限度内.
【解析】
(2) 行驶的总路程为:,共用了 .
【知识点】用函数图象表示实际问题中的函数关系
