2021-2022学年人教版初中数学九年级下册27.2.2相似三角形的性质教学课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年人教版初中数学九年级下册27.2.2相似三角形的性质教学课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 471.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
相似三角形的性质
复习
例题
小结
定理
填空:
两个相似三角形的_______相等,_______成比例。
_________________________、
____________________________、
________________________________都等于相似比。
对应角
对应边
相似三角形对应高的比
相似三角形对应中线的比
相似三角形对应角平分线的比
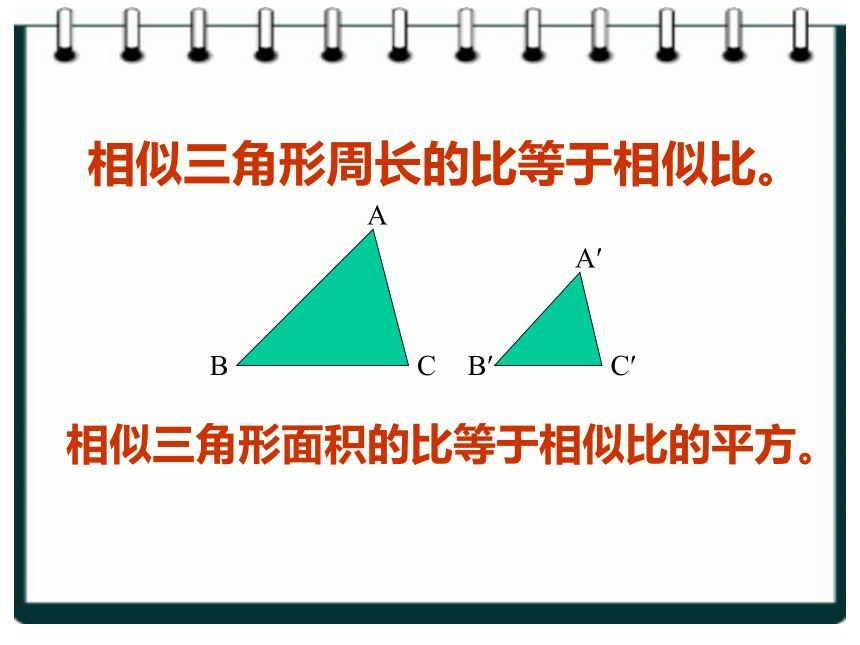
相似三角形周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
A
C
B
B′
A′
C′
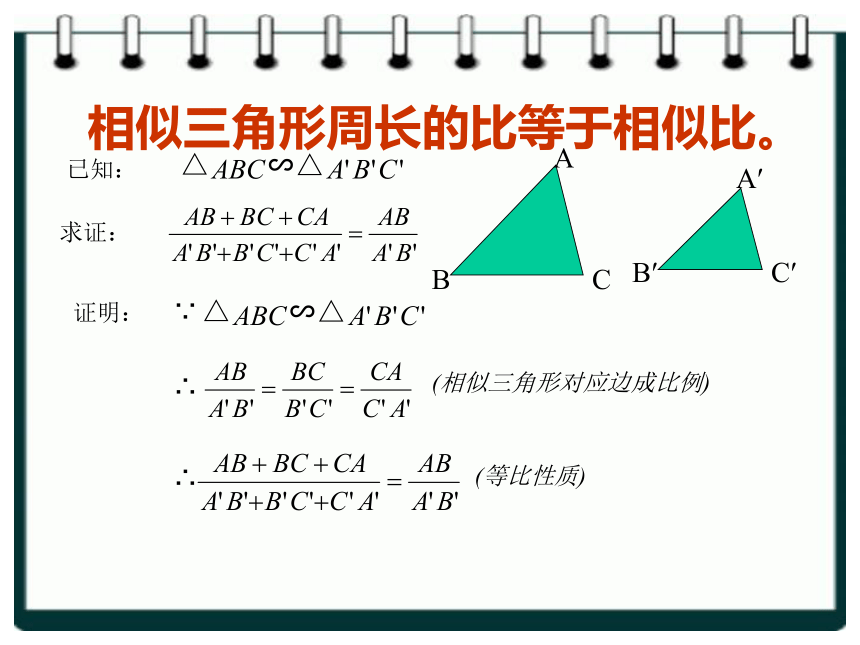
相似三角形周长的比等于相似比。
已知:
求证:
∽△
△
证明:
∽△
△
∵
∴
∴
(相似三角形对应边成比例)
(等比性质)
A
C
B
B′
A′
C′
相似三角形面积的比等于相似比的平方。
已知:
求证:
∽△
△
A
B
C
A′
B′
C′
D
D′
证明:
分别过A、A′,
作AD⊥BC于D,
∴
∵
∽ △
△
∴
∴
(相似三角形对应边成比例)
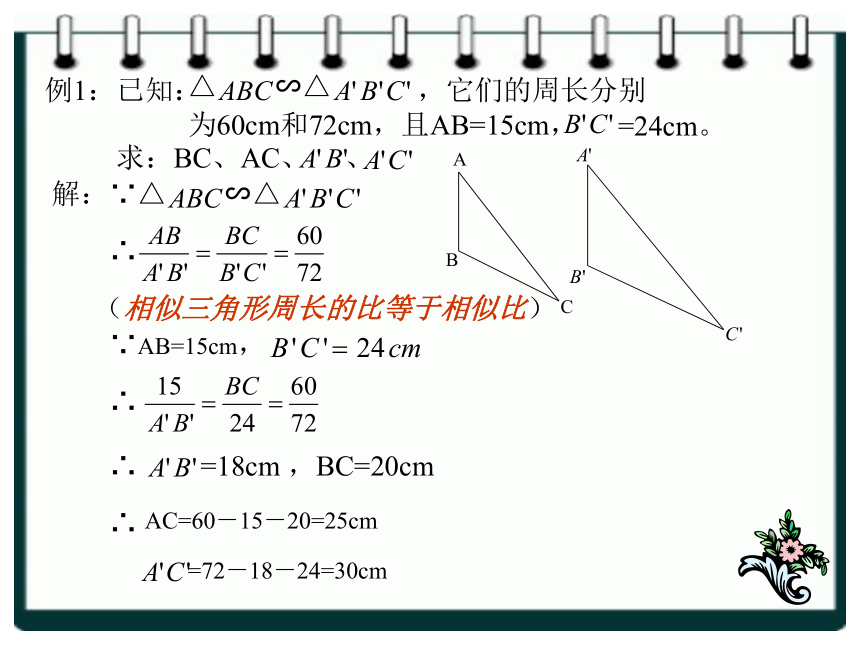
例1:已知: ,它们的周长分别 为60cm和72cm,且AB=15cm,
∽△
△
=24cm。
求:BC、AC、 、
A
B
C
解:∵
∽△
△
∴
(相似三角形周长的比等于相似比)
∵AB=15cm,
∴
∴
=18cm ,BC=20cm
∴
AC=60-15-20=25cm
=72-18-24=30cm
例1:已知: ,它们的周长分别 为60cm和72cm,且AB=15cm,
∽△
△
=24cm。
求:BC、AC、 、
A
B
C
解:∵
∽△
△
∴
(相似三角形周长的比等于相似比)
∵AB=15cm,
∴
∴
=18cm ,BC=20cm
∴
AC=60-15-20=25cm
=72-18-24=30cm
例2:如图所示,D、E分别是AC、AB上的点,
A
B
C
D
E
已知△ABC的面积为 ,
求四边形BCDE的面积。
解:∵
,∠A=∠A
∴
∽△
△
∴
(相似三角形面积的比等于相似比的平方)
∴
∵
∴
∴
∴
(两边对应成比例,且夹角相等,两三角形相似)
练习:
已知:
∽△
△
,它们的周长分别
为144cm和120cm ,且BC=48cm,
1、
A
D
C
B
△
已知:如图,Rt
ABC,CD为斜边AB上的高,
求:
2、
3、三角形的一条中位线把三角形截成的一个小
三角形与原三角形的周长之比等于________,
面积之比等于________。
1:2
1:4
4、两个相似三角形对应的中线长分别是6cm和
18cm,若较大三角形的周长是42cm,面积是
,则较小三角形的周长为________cm,
面积为____ 。
14
4
5、已知:如图△ABC中,DE∥BC,AF⊥DE
垂足为F,AF交BC于G。若AF=5,FG=3,
则
A
F
E
D
B
C
G
H
N
M
F
E
D
C
B
A
6、如图在 ABCD中,E是BC的中点,是BE的中点,
AE与DF交于点H,过点H作MN⊥AD,垂足为M,
交BC于N,则NH:MH=______。
5
8
5
8
25
64
1:4
思考题:
A
B
D
C
E
在△ABC中,BC=m,DE∥BC,交AB于E,交AC于D, 求DE的长度。
这节课我们学习了相似三角形的另一重要性质:相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方。
小结:
作业:
教材习题
相似三角形的性质
复习
例题
小结
定理
填空:
两个相似三角形的_______相等,_______成比例。
_________________________、
____________________________、
________________________________都等于相似比。
对应角
对应边
相似三角形对应高的比
相似三角形对应中线的比
相似三角形对应角平分线的比
相似三角形周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
A
C
B
B′
A′
C′
相似三角形周长的比等于相似比。
已知:
求证:
∽△
△
证明:
∽△
△
∵
∴
∴
(相似三角形对应边成比例)
(等比性质)
A
C
B
B′
A′
C′
相似三角形面积的比等于相似比的平方。
已知:
求证:
∽△
△
A
B
C
A′
B′
C′
D
D′
证明:
分别过A、A′,
作AD⊥BC于D,
∴
∵
∽ △
△
∴
∴
(相似三角形对应边成比例)
例1:已知: ,它们的周长分别 为60cm和72cm,且AB=15cm,
∽△
△
=24cm。
求:BC、AC、 、
A
B
C
解:∵
∽△
△
∴
(相似三角形周长的比等于相似比)
∵AB=15cm,
∴
∴
=18cm ,BC=20cm
∴
AC=60-15-20=25cm
=72-18-24=30cm
例1:已知: ,它们的周长分别 为60cm和72cm,且AB=15cm,
∽△
△
=24cm。
求:BC、AC、 、
A
B
C
解:∵
∽△
△
∴
(相似三角形周长的比等于相似比)
∵AB=15cm,
∴
∴
=18cm ,BC=20cm
∴
AC=60-15-20=25cm
=72-18-24=30cm
例2:如图所示,D、E分别是AC、AB上的点,
A
B
C
D
E
已知△ABC的面积为 ,
求四边形BCDE的面积。
解:∵
,∠A=∠A
∴
∽△
△
∴
(相似三角形面积的比等于相似比的平方)
∴
∵
∴
∴
∴
(两边对应成比例,且夹角相等,两三角形相似)
练习:
已知:
∽△
△
,它们的周长分别
为144cm和120cm ,且BC=48cm,
1、
A
D
C
B
△
已知:如图,Rt
ABC,CD为斜边AB上的高,
求:
2、
3、三角形的一条中位线把三角形截成的一个小
三角形与原三角形的周长之比等于________,
面积之比等于________。
1:2
1:4
4、两个相似三角形对应的中线长分别是6cm和
18cm,若较大三角形的周长是42cm,面积是
,则较小三角形的周长为________cm,
面积为____ 。
14
4
5、已知:如图△ABC中,DE∥BC,AF⊥DE
垂足为F,AF交BC于G。若AF=5,FG=3,
则
A
F
E
D
B
C
G
H
N
M
F
E
D
C
B
A
6、如图在 ABCD中,E是BC的中点,是BE的中点,
AE与DF交于点H,过点H作MN⊥AD,垂足为M,
交BC于N,则NH:MH=______。
5
8
5
8
25
64
1:4
思考题:
A
B
D
C
E
在△ABC中,BC=m,DE∥BC,交AB于E,交AC于D, 求DE的长度。
这节课我们学习了相似三角形的另一重要性质:相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方。
小结:
作业:
教材习题
