2021-2022学年人教版八年级数学下册16.2二次根式的乘除教学课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册16.2二次根式的乘除教学课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 533.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 19:58:52 | ||
图片预览






文档简介
(共27张PPT)
二次根式的乘除2
1
难点名称:合理简洁地进行二次根式的除法运算
八年级-下册-16.2
学 习 目 标
1.理解二次根式的除法法则及商的算术平方根的性质.(重点)
2.合理简洁地进行二次根式的除法运算.(难点)
复习旧知
a
(a≥0)
(a≤0)
=
=|a|
(a≥ 0)
(1) ≥0 (a≥0)
双重非负性
二次根式的性质:
a
-a
问题1 当a 是正数或0 时, 是实数吗?取a 值分
别为1,2,3,4,5试一试!
类比有理数的运算,你认为任何两个实数之间可以
进行哪些运算?
加、减、乘、除四则运算
思考
问题2 两个二次根式能否进行加、减、乘、除运算?怎样运算?让我们从研究乘法开始.
请写出两个二次根式,猜一猜,它们的积应该是多少?
特殊化,从能开得尽方的
二次根式乘法运算开始思考!
?
讲授新课
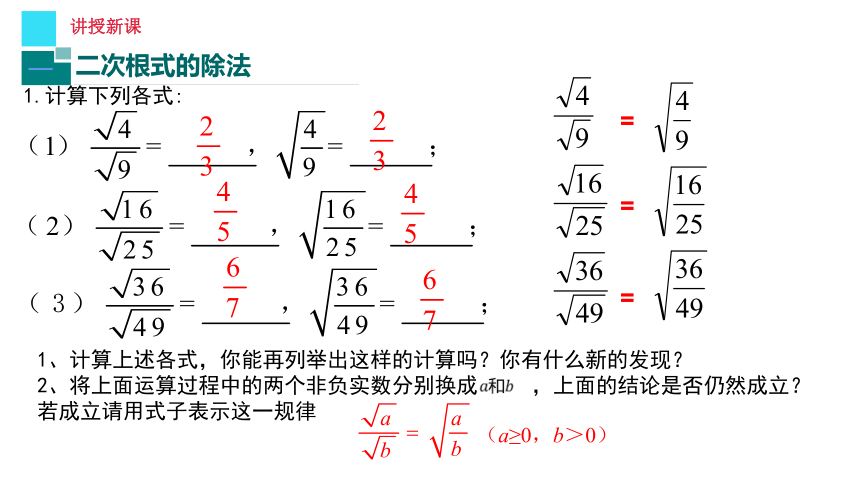
二次根式的除法
一
1.计算下列各式:
1、计算上述各式,你能再列举出这样的计算吗?你有什么新的发现?
2、将上面运算过程中的两个非负实数分别换成 ,上面的结论是否仍然成立?
若成立请用式子表示这一规律
(a≥0,b>0)
=
=
=
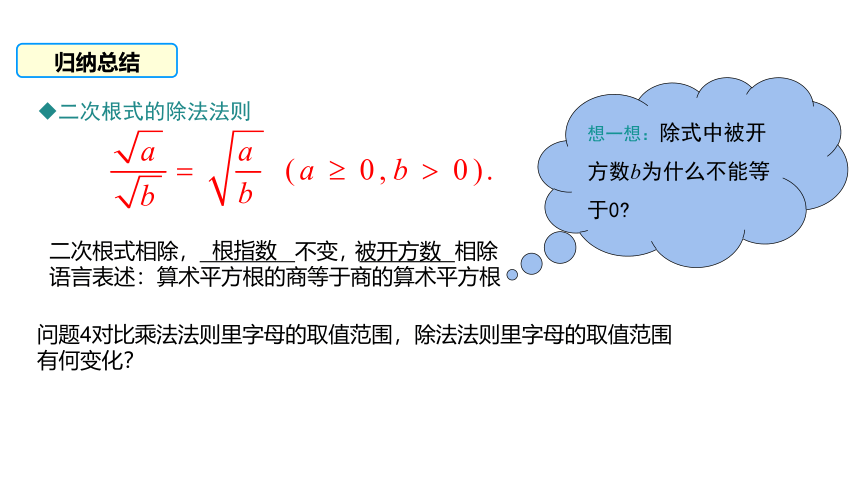
归纳总结
二次根式的除法法则
首页
想一想:除式中被开方数b为什么不能等于0
二次根式相除, 不变, 相除
语言表述:算术平方根的商等于商的算术平方根
问题4对比乘法法则里字母的取值范围,除法法则里字母的取值范围有何变化?
根指数
被开方数
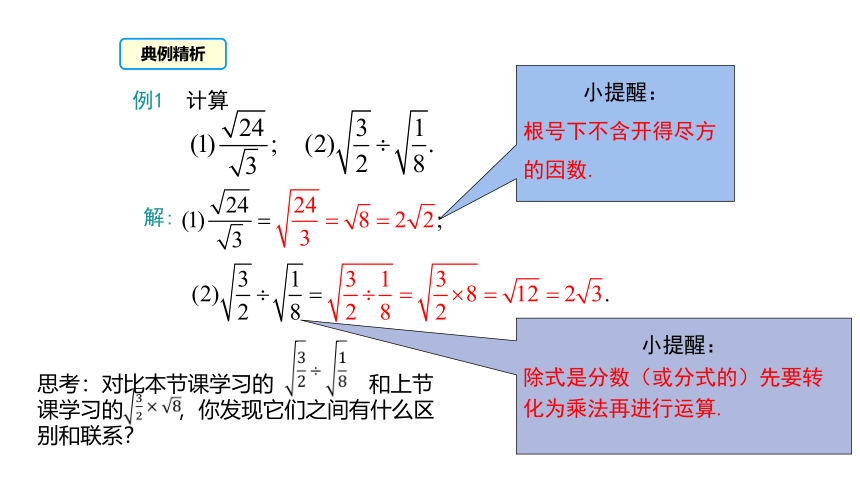
典例精析
例1 计算
解:
小提醒:
根号下不含开得尽方的因数.
小提醒:
除式是分数(或分式的)先要转化为乘法再进行运算.
思考:对比本节课学习的 和上节课学习的 ,你发现它们之间有什么区
别和联系?
你还记得单项式除以单项式法则吗?试回顾如何计算
形如 的除法
二
归纳总结
二次根式的除法扩充法则
想一想:如何计算 呢?
试回顾如何计算 ?
课堂练习
10
解:原式
难点巩固
解:原式
首页
二次根式的商的算术平方根的性质
类似的,把二次根式的除法法则反过来,就得到
商的算术平方根的性质及应用
三
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
小提醒:
记住成立的条件!
归纳:
利用它可以进行二次根式的化简
例5 化简
解:
典例精析
还有其他解法吗
补充解法:
A组:
典例精析
、
归纳
利用 达到去掉根号的目的
例5 化简
典例精析
例7 化简
B组:
解:
归纳
化简二次根式的步骤:
1.将被开方数尽可能分解成几个平方数
2.应用积(或商)的算术平方根的性质
3.将平方项应用 化简
4.二次根式运算的结果中,被开方数不含能开得尽方的因数或因式
课堂练习
15
难点巩固
、
归纳
拓展应用,能力提升
二次根式乘除混合运算:
1、当所得二次根式的被开方数的因数(式)中,有一些幂的指数不小于2,即含有完全平方的因式(数),我们就可利用积的算术平方根的性质,并用
来化简二次根式。
2、二次根式的乘除混合运算,先把根号外的系数依次相乘除,再把根号下的被开方数依次相乘除,最后再化简二次根式。
的值是( )
的值是( )
的值是( )
A
B
A
做一做
4. 估计
的运算结果应在( )
A、1到2之间 B、2到3之间
C、3到4之间 D、4到5之间
C
5. 比较大小
<
<
典例精析
解:(1) ;
2.计算:
(1) ;(2) .
(2) .
变:若(2)的条件为a≤0,b≥0呢?
3.计算:
(1) ;(2) ;(3) .
解:(1) ;
(2) ;
(3) .
2.将下列式子中根号外的因数(因式)移到根号内.
A
做一做
4.己知 是不大于100的整数,求整数x的值.
随堂练习
课堂小结
(1)二次根式的乘法运算的依据是什么?
(2)在本节课学习中你认为容易出错的地方在哪里?
出错的原因是什么?
二次根式的乘除2
1
难点名称:合理简洁地进行二次根式的除法运算
八年级-下册-16.2
学 习 目 标
1.理解二次根式的除法法则及商的算术平方根的性质.(重点)
2.合理简洁地进行二次根式的除法运算.(难点)
复习旧知
a
(a≥0)
(a≤0)
=
=|a|
(a≥ 0)
(1) ≥0 (a≥0)
双重非负性
二次根式的性质:
a
-a
问题1 当a 是正数或0 时, 是实数吗?取a 值分
别为1,2,3,4,5试一试!
类比有理数的运算,你认为任何两个实数之间可以
进行哪些运算?
加、减、乘、除四则运算
思考
问题2 两个二次根式能否进行加、减、乘、除运算?怎样运算?让我们从研究乘法开始.
请写出两个二次根式,猜一猜,它们的积应该是多少?
特殊化,从能开得尽方的
二次根式乘法运算开始思考!
?
讲授新课
二次根式的除法
一
1.计算下列各式:
1、计算上述各式,你能再列举出这样的计算吗?你有什么新的发现?
2、将上面运算过程中的两个非负实数分别换成 ,上面的结论是否仍然成立?
若成立请用式子表示这一规律
(a≥0,b>0)
=
=
=
归纳总结
二次根式的除法法则
首页
想一想:除式中被开方数b为什么不能等于0
二次根式相除, 不变, 相除
语言表述:算术平方根的商等于商的算术平方根
问题4对比乘法法则里字母的取值范围,除法法则里字母的取值范围有何变化?
根指数
被开方数
典例精析
例1 计算
解:
小提醒:
根号下不含开得尽方的因数.
小提醒:
除式是分数(或分式的)先要转化为乘法再进行运算.
思考:对比本节课学习的 和上节课学习的 ,你发现它们之间有什么区
别和联系?
你还记得单项式除以单项式法则吗?试回顾如何计算
形如 的除法
二
归纳总结
二次根式的除法扩充法则
想一想:如何计算 呢?
试回顾如何计算 ?
课堂练习
10
解:原式
难点巩固
解:原式
首页
二次根式的商的算术平方根的性质
类似的,把二次根式的除法法则反过来,就得到
商的算术平方根的性质及应用
三
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
小提醒:
记住成立的条件!
归纳:
利用它可以进行二次根式的化简
例5 化简
解:
典例精析
还有其他解法吗
补充解法:
A组:
典例精析
、
归纳
利用 达到去掉根号的目的
例5 化简
典例精析
例7 化简
B组:
解:
归纳
化简二次根式的步骤:
1.将被开方数尽可能分解成几个平方数
2.应用积(或商)的算术平方根的性质
3.将平方项应用 化简
4.二次根式运算的结果中,被开方数不含能开得尽方的因数或因式
课堂练习
15
难点巩固
、
归纳
拓展应用,能力提升
二次根式乘除混合运算:
1、当所得二次根式的被开方数的因数(式)中,有一些幂的指数不小于2,即含有完全平方的因式(数),我们就可利用积的算术平方根的性质,并用
来化简二次根式。
2、二次根式的乘除混合运算,先把根号外的系数依次相乘除,再把根号下的被开方数依次相乘除,最后再化简二次根式。
的值是( )
的值是( )
的值是( )
A
B
A
做一做
4. 估计
的运算结果应在( )
A、1到2之间 B、2到3之间
C、3到4之间 D、4到5之间
C
5. 比较大小
<
<
典例精析
解:(1) ;
2.计算:
(1) ;(2) .
(2) .
变:若(2)的条件为a≤0,b≥0呢?
3.计算:
(1) ;(2) ;(3) .
解:(1) ;
(2) ;
(3) .
2.将下列式子中根号外的因数(因式)移到根号内.
A
做一做
4.己知 是不大于100的整数,求整数x的值.
随堂练习
课堂小结
(1)二次根式的乘法运算的依据是什么?
(2)在本节课学习中你认为容易出错的地方在哪里?
出错的原因是什么?
