高中数学填空题综合专练(267题,含答案)
文档属性
| 名称 | 高中数学填空题综合专练(267题,含答案) | 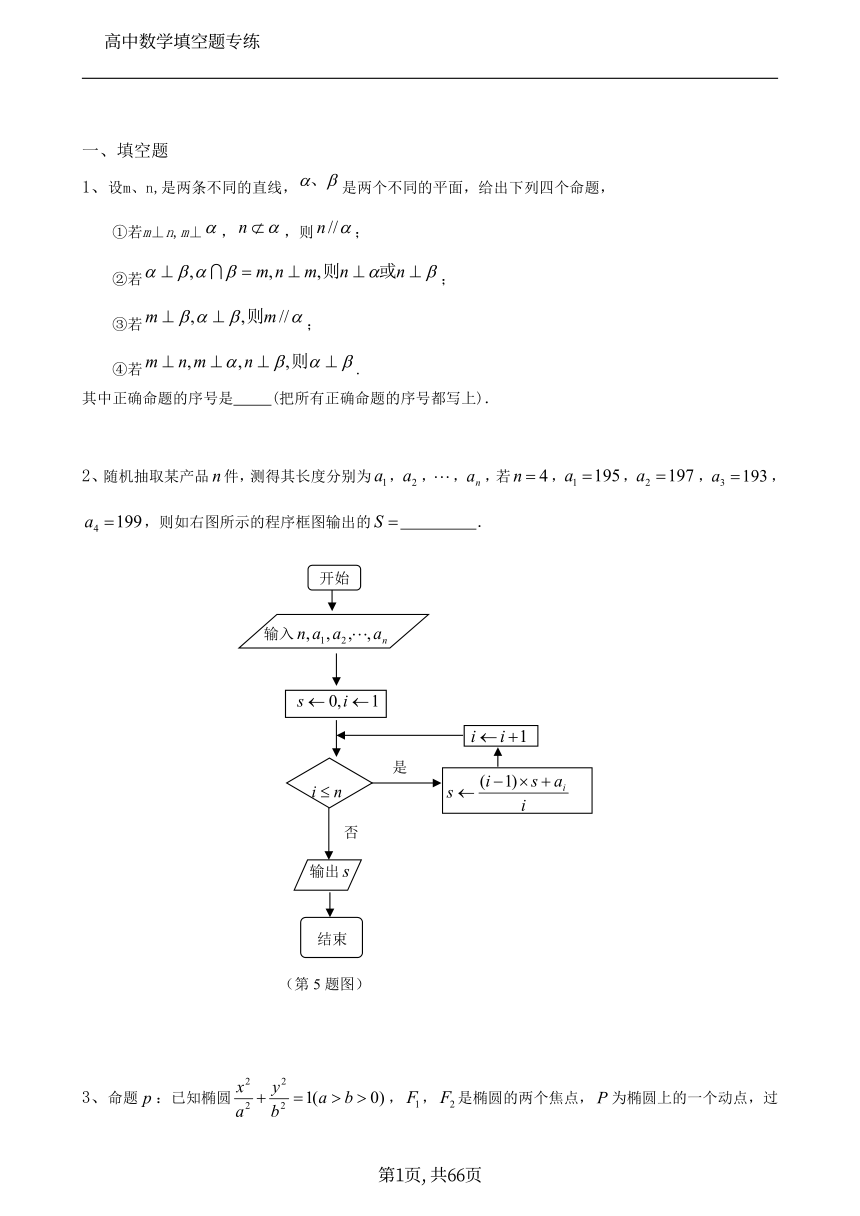 | |
| 格式 | |||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 17:27:39 | ||
图片预览





文档简介
高中数学填空题专练
一、填空题
1、设m、n,是两条不同的直线, 、 是两个不同的平面,给出下列四个命题,
①若m⊥n,m⊥ ,n ,则 n // ;
②若 , m,n m,则n 或n ;
③若m , ,则m // ;
④若m n,m ,n ,则 .
其中正确命题的序号是 (把所有正确命题的序号都写上).
2、随机抽取某产品 n件,测得其长度分别为 a1,a2 , ,an ,若n 4,a1 195,a2 197 ,a3 193,
a4 199,则如右图所示的程序框图输出的 S .
开始
输入 n,a1,a2 , ,an
s 0, i 1
i i 1
是
i n s (i 1) s a i
i
否
输出 s
结束
(第 5 题图)
p x
2 y2
3、命题 :已知椭圆 2 2 1(a b 0) ,F1,F2 是椭圆的两个焦点,P为椭圆上的一个动点,过a b
第1页,共66页
高中数学填空题专练
F2作 F1PF2 的外角平分线的垂线,垂足为M ,则OM 的长为定值.类比此命题,在双曲线中也有命题q:
x2 y2
已知双曲线 2 2 1(a b 0), F1, F2 是双曲线的两个焦点, P为双曲线上的一个动点,过 F 作a b 2
F1PF2 的 的垂线,垂足为M ,则OM 的长为定值.
2 2
4、设点 (a,b)在平面区域D (a,b) a 1, b 1 x y中均匀分布出现,则双曲线 2 2 1(a b 0)的离a b
心率 e满足1 e 2 的概率为 .
5、. O 2设点 是 ABC的三边中垂线的交点,且 AC 2AC AB 2 0 ,则 BC AO的范围是 .
6、 0已知向量a,b满足|a|=2,|b|=1,a与b的夹角为60 ,则|a-2b|等于 .
7、 如图,正六边形 ABCDEF 的两个顶点 A、D 为椭圆的两个焦点,
其余 4 个顶点在椭圆上,则该椭圆的离心率是 .
x 2 y 2
2 2 1(a 0,b 0)
2 3
8、 2已知双曲线 a b 的离心率为 3 ,焦距为2c,且2a =3c,双曲线 上一点P满足
PF1 PF2 2(F1、F2为左右焦点),则 | PF1 | | PF2 | .
9、已知复数 z i(i 3)( i是虚数单位),则复数 z的虚部为 .
10、函数 f x sin x cos x 2的单调递增区间是 ;
1 4
11、已知正项等比数列 an 满足 a7 a6 2a5 ,若存在两项 am、an使得 aman 4a1 ,则 的最小m n
值是 ;
第2页,共66页
高中数学填空题专练
12、对于不等式 y ax2 bx c 2来说,它的几何意义是抛物线 y ax bx c内部(即包含焦点的部分),
y x2 3x 3
y x
那么由不等式组 所确定的图形的面积是 。
y 0
x 3
1 1
13、计算 (lg lg 25) 100 2 = .
4
1
(lg 1 lg 25) 100 2 =(-lg4-lg25) 1 (lg 4 lg 25) 10 lg(4 25 ) 10
4 10
lg(102 10 2 10 20
14、设 f (x) 是定义在R上的奇函数,当x≤0时, f (x) = 2x2 x,则 f (1) .
0, 15、 2设 ,则方程 x cos y
2 sin 1所表示的曲线不可能是-------- ( )
2
A.两条直线 B.圆 C.椭圆 D.双曲线
16、小明爸爸开车以80km/h的速度沿着正北方向的公路行驶,小明坐在车里向外观察,在点A处望见电视
0 0
塔P在北偏东30 方向上,15分钟后到点B处望见电视塔在北偏东75 方向上,则汽车在点B时与电视塔P的距
离是 km.
17、用分层抽样的方法从某高中学校学生中抽取一个容量为 55 的样本参加问卷调查,其中高一年级、高
二年级分别抽取 10 人、25 人。若该校高三年级共有学生 400 人,则该校高一和高二年级的学生总数为
人。
, sin 3 tan 18、已知 , ,则 = ——
2 5 4
19、 O 2 2过原点 作圆 x y 6x 8y 20 0的两条切线,设切点分别为 P、Q,则线段 PQ 的长为——
第3页,共66页
高中数学填空题专练
20、如图,从圆O外一点 P引圆O的切线 PA和
割线 PBC,已知PA 2 2 , PC 4,
圆心O到 BC的距离为 3 ,则圆O的
半径为 .
C B P
O
A
21、已知等差数列 an 的前 n项和为 Sn,若 a4 18 a5 ,则 S8 .
22、若把英语单词“ good ”的字母顺序写错了,则可能出现的错误共有 种.
f (x) log x x b(a 0, a 1) 1 123、已知函数 a 且 ,当 a 且3 b 4时,3 2
函数 f (x) 的零点 x0 (n,n 1),n N
*
,则 n .
24、 x x 2不等式 4 2 0的解集为 .
x2 y2
25、已知双曲线 2 1(b 0) 的一条渐近线的倾斜角为 ,则b的值为 。9 b 3
26、已知集合 P (x, y) x y 0 ,Q (x, y) x y 2 ,则Q P .
第4页,共66页
高中数学填空题专练
27、用 3 种不同的颜色给图中的 3 个矩形随机涂色,每个矩形只涂一种颜色,则 3 个矩形中有且仅有两个
矩形颜色相同的概率是 。
2 2
28、在平面直角坐标系 xOy x y中,已知椭圆 2 a b2
1(a b 0) 的右顶点为 A,上顶点为 B,M 为线段
AB o的中点,若 MOA 30 ,则该椭圆的离心率的值为 。
29、已知等比数列 a 2n 的各均为正数,且 a1 2a2 3,a4 4a3a7 ,则数列 an 的通项公式为 。
30、 m R 2 2设 ,已知函数 f (x) x 2mx (1 2m)x 3m 2 ,若曲线 y f (x) 在 x 0处的切线恒
过定点 P,则点 P 的坐标为 。
f (x), f (x) k ,
31、设函数 y f (x) 在 R 内有定义,对于给定的正数 k,定义函数 fk (x) ,若函数
k , f (x) k.
f (x) log3 | x |
1
,则当 k 时,函数 fk (x) 的单调减区间为 。3
32、 2已知数列{ an }的前 n项和 Sn n 9n,若它的第 k项满足5 ak 8,则 k .
15
33、若 z z z 2i( i为虚数单位),则复数 z = 。
4
34、
为 .
35、已知直线上 n 个点最多将直线分成 C 0 1n Cn n 1 段,平面上 n 条直线最多将平面分成
2
C 0n C
1 C 2 n n 2n n 部分(规定:若 k n,则C
k
n 0),则类似地可以推算得到空间里 n个平面最2
第5页,共66页
高中数学填空题专练
多将空间分成 部分
36、已知 AB AC,| AB AC | 2 ,点M 是线段BC上的一点,且 AM (AB AC) 1,则 | AM |的
取值范围是 .
37、 x2经过圆 2x y2 0 的圆心C,且与直线 x y 0垂直的直线方程是 .
38、若 (x 2)5 a x55 a4x
4 a 33x a2x
2 a1x a0 ,则 a1 a2 a3 a4 a5 _______。
2 3
39、甲、乙两人分别独立参加某高校自主招生面试,若甲、乙能通过面试的概率分别是 ,和 ,则面
3 4
试结束后通过的人数 的数学期望 E 是
40、若 lga+lgb=0(a≠1),则函数 f(x)=ax与 g x x( )=-b 的图象关于________对称.
41、某几何体的三视图如下图所示,则该几何体的表面积为___________
42、 汽车的最佳使用年限是使年均消耗费用最低的年限(年均消耗费用=年均成本费用+年均维修
费),设某种汽车的购车的总费用为 50000 元;使用中每年的保险费、养路费及汽油费合计为 6000 元;
x 2前 年的总维修费 y 满足 y ax bx ,已知第一年的总维修费为 1000 元,前两年的总维修费为 3000
元,则这种汽车的最佳使用年限为 年.
第6页,共66页
高中数学填空题专练
ABC BA BC
43、已知在 中, A 120 ,记 ,
CA CB ,
| BA | cos A | BC | cosC |CA | cos A |CB | cosB
则向量 与 夹角的大小为 .
三,解答题:本大题共 5 小题,共 72 分,解答应写出文字说明、证明过程或演算步骤。
44、若 i为虚数单位,则 (1 i)i .
45、若对于定义在 R上的函数 f (x) ,其图象是连续不断的,且存在常数 ( R),使得对任意实数 x都有
f (x + ) + f (x) = 0成立,则称 f (x) 是一个“ —伴随函数”. 有下列关于“ —伴随函数”的结论:
①f (x) =0 是常数函数中唯一个“ —伴随函数”;② f (x) = x2是一个“ —伴随函数”;
1
③ “ —伴随函数”至少有一个零点. 其中不.正.确.的序号是______.2
46、(优选法与试验设计初步) 用 0.618 法寻找实验的最优加入量时,若当前存优范围是[628,774],好点
是 718,则此时要做试验的加入点值是 。
47、定义在 R 上的奇函数 f (x) 满足: x 0时 f (x) 2 x b 则 f (2) = 。
x 3y 7 0
48、 已知 x, y满足 x 1 ,则 z | y x |的最大值为 .
y 1
2cos
x x 2000
49、已知函数 f (x) 3 ,则 f f 2012 .
x 100 x 2000
x 2
50、如图所示,直线 x 2 与双曲线C : y 2 1的渐近线交于 E1 , E2 两点,记OE1 e4 1
,OE2 e2 ,
任取双曲线C上的点 P,若OP ae1 be2 ,则实数 a和b满足的一个等式是_____________.
第7页,共66页
高中数学填空题专练
51、(坐标系与参数方程选做题)在极坐标系中,直线 l的方程为3 sin 4 cos 2,则点( 2, )
4
到直线 l的距离为 .
52、如图4所示,圆O的直径AB=6,C为圆周
上一点, BC 3过C作圆的切线 l,过A作 l的垂线AD,垂足为D,
则∠DAC= .
53、函数 f(x)= x + x(x-2)的定义域是 .
54、若 z(1 i) 1 i ( i是虚数单位),则 z的共轭复数 z =_____________ .
55、设集合 A x | x 1 ,B x | x a ,则“ A B R”是“a=1”的___________条件.(从如下
四个中选一个正确的填写:充要条件、充分不必要条件、必要不充分条件、既不充分也不必要条件)
第8页,共66页
高中数学填空题专练
56、从某小学随机抽取 100 名同学,这些同学身高都不低于 100 厘米,将他们身高(单位:厘米)数据绘
制成频率分布直方图(如右图).现用分层抽样的方法从身高在[120,130﹚,[130,140﹚,[140,150]
三组学生中,选取 18 人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
57、 M (2,1) x2已知点 是抛物线 2py上的点,则以点M 为切点的抛物线的切线方程为
.
58、已知函数 f (x) | lg x |.若 f (a) f (b)且 a b,则 a b的取值范围是 .
59、一个袋子里装有大小相同的 3个红球和 2 个黄球,从中同时取出 2 个球,则其中含红球个数的数学期
望是 .
60、某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第 k棵树种植在点 Pk (xk,yk )
x k 1 k 2 k xk 1 1 5 T
5
T ,
x 1 y 1 k 2
5
≥ 处,其中 1 , 1 ,当 时,
y y T k 1 k 2 k
k 1 T
.
5
5
T (a)表示非负实数a的整数部分,例如T (2.6) 2 ,T (0.2) 0.按此方案第 2012 棵树种植点的坐
标应为______________.
第9页,共66页
高中数学填空题专练
4
61、计算: log 273 lg 25 2lg 2 e
ln 2
3
62、 f (x) xn
2 3n (n Z) 是偶函数,且 y f (x) 在 (0, )上是减函数,则 n
63、 2若关于 x的方程3tx (3 7t)x 4 0 的两实根 , ,满足 0 1 2 ,则实数 t的取值范
围是 。
x2 y2
64、 过双曲线 2 2 1(a 0,b 0) 的右焦点F和虚轴端点B作一条直线,若右顶点A到直线Fa b
b
B的距离等于 ,则双曲线的离心率 e
7
65、一个几何体的三视图如图所示,
则此几何体的体积是 .
3
4
正视图 侧视图
4
4
俯视图
第10页,共66页
高中数学填空题专练
66、若圆 x 2 y 2 2x 4y 1 0 关于直线 2ax-by+2=0(a,b∈R)对称,则 ab的取值范围是
___ .
67、一个几何体的三视图如图所示,则该几何体的体积为 .
68、已知 a (m,n),b ( p,q) ,定义 a b mn pq,下列等式中
① a a 0;②a b b a;③ (a b) a a a b a;
2 2
④ (a b) (a b) (m2 q2 )(n2 p2 )
一定成立的是 。(填上序号即可)
69、统计某校 1000 名学生的数学会考成绩,得到样本频率分布直方图如下图,规定不低于 60 分为及格,
不低于 80 分为优秀.则及格人数是 ;优秀率为 .
第11页,共66页
高中数学填空题专练
70、已知向量 a ( 3,1) ,b (0,1) c , (k , 3) ,若 a 2b 与 c 垂直,则 k .
71、设 a log 3 ,b ln 3, c 2 11 ,则这三个数由大到小的顺序为_________.(用“ ”连结各数)
2
72、已知 sin 5 ,则 cos 2 _____________.
5
2 2
73、已知椭圆C : x y1 2 2 1( a b 0 ,且 a,b为常数),椭圆C2 焦点在 y 轴上,椭圆C2 的长轴长与a b
椭圆C1 的短轴长相等,且椭圆C1 与椭圆C2 的离心率相等,则椭圆C2 的方程
为: .
74、设 z 1 i(i 2是虚数单位),则
z 2
z .
75、给出下列命题,其中正确的命题是 (写出所有正确命题的编号).
..
① 非零向量 a、 b满足 | a | | b | | a b | ,则 a与a b的夹角为30 ;
② 已知非零向量 a、 b,则“ a b 0 ”是“ a、 b的夹角为锐角”的充要条件;
③ 命题“在三棱锥O ABC中,已知OP xOA yOB 2OC,若点 P在△ABC所在的平面内,
则 x y 3”的否命题为真命题;
④ 若 (AB AC) (AB AC) 0,则△ABC为等腰三角形.
76、在等比数列 an 中, a1 1 ,公比 q 2 .若 an 64 ,则 n的值为
x y 4
77、当 x , y 满足不等式组 x 4 y时,点 (4,0)为目标函数 z ax 2y取得最大值时的最优解,则实
x 4
数 a的取值范围是
第12页,共66页
高中数学填空题专练
78、圆C的半径为 1,过点 P作圆C的两条切线,切点分别为 A , B .则 PA PB的最小值为
x2 y2
79、双曲线 1上一点 P 到右焦点的距离是实轴两端点到右焦点距离的等差中项,则 P 点到左焦
16 9
点的距离为 .
80、若不等式 (x y)(1 x y) 1对一切实数 x恒成立,则实数 y 的取值范围是 .
81、定义在 R 上的函数 y f (x) ,对任意不等的实数 x1, x2 都有[ f (x1) f (x2)](x1 x2) 0成立,又
函数 y f (x 1) 2的图象关于点 (1,0) 对称,若不等式 f (x 2x) f (2y y2 ) 0成立,则当1 x 4时,
y
的取值范围为 .
x
82、已知函数 y f (x) 是 R上的偶函数,对 x R都有 f (x 4) f (x) f (2)
成立.当 x , x 0,2 ,且 x x f (x时,都有 1) f (x2 )1 2 1 2 0 ,给出下列命题:x1 x2
(1) f (2) 0;
(2)直线 x 4是函数 y f (x) 图象的一条对称轴;
(3)函数 y f (x) 在 4,4 上有四个零点;
(4) f (2012) f (0)
其中正确命题的序号为__________(把所有正确命题的序号都填上).
第13页,共66页
高中数学填空题专练
2
83、幂函数 y (m2 m 1) xm 2m 3 ,当 x (0, ) 时为减函数,则实数 m 的值为
84、在 x a 10 7的展开式中, x 的系数是 15,则实数 a = ——
85、 2若 sin sin 1,则 cos 4 cos 2 = ——
86、 O x 2过原点 作圆 y 2 6x 8y 20 0的两条切线,设切点分别为 P、Q,则直线 PQ 的方程是——
87、对于 ABC,有如下命题:①若 sin 2A sin 2B ,则 ABC为等腰三角形;②若 sin A cosB则 ABC
2 2
为直角三角形;③若 sin A sin B cos 2 C 1则 ABC为钝角三角形.其中正确命题的序号是——
88、已知 x 0 , y 0 4 1 且 1,则 x y最小值是 .
x y
89、如图,已知图中的三个直角三角形是一个几何体的三视图,
那么这个几何体的体积等于_______.
第14页,共66页
高中数学填空题专练
90、若等差数列 {a n }的首项为 a1 ,公差为 d ,
S
前 n项的和为 Sn,则数列 { n }为等差数列,n
S d
且通项为 n a1 (n 1) 。类似地,请完成n 2
下列命题:若各项均为正数的等比数列 {bn }
的首项为 b1,公比为 q,前 n项的积为Tn,
则数列 。
13
7
3 15
91、对于大于 1 3 3 3 的自然数 m 的三次幂可以用技术进行以下方式的“分裂”:2 ,3 9 ,4 5
, ……
17
11
19
3
仿此,若m 的“分裂数”中有一个是 59,则m
92、若函数 f (x) a sin 2x b tan x 1,且 f (2) 5, 则 f ( 2) f ( ) __________
93、 f (x) | x | sin x 1已知函数 (x R)的最大值为M ,最小值为m,则M m ______
| x | 1
94、下列几个命题:
2
①方程 x (a 3)x a 0有一个正实根,一个负实根,则 a 0;
2 2
②函数 y x 1 1 x 是偶函数,但不是奇函数;
③函数 f (x) 的值域是[ 2,2],则函数 f (x 1)的值域为[ 3,1];
④设函数 y f (x) 定义域为 R,则函数 y f (1 x) 与 y f (x 1) 的图象关于 y 轴对称;
y | 3 x2⑤一条曲线 |和直线 y a (a R)的公共点个数是m,则m的值不可能是 1.
其中正确的有_________________
第15页,共66页
高中数学填空题专练
95、观察下列等式:
(1 x x2 )1 1 x x2 ,
(1 x x2 )2 1 2x 3x2 2x3 x4 ,
(1 x x2 )3 1 3x 6x2 7x3 6x4 3x5 x6 ,
(1 x x2 )4 1 4x 10x2 16x3 19x4 16x5 10x6 4x7 x8 ,
�
由以上等式推测:
n N , (1 x x2 )n a a x a x2 a x2n对于 若 0 1 2 2 n ,则 a2 .
96、如图,圆O是 ABC的外接圆,过点C的切线交 AB的延长线于点D,CD 2 7, AB BC 3,则 AC
的长为 .
C
D
O
B
A
97 、 在 (1 2x)3 (1 2 x )3 (1 33 x )3 的 展 开 式 中 , x 的 系 数
为 .(用数字作答)
98、若 A {x | y x 1},B {y | y x2 1},则A B= 。
99、已知 tan 2,
则1 1 sin 2 3cos2 .
2
第16页,共66页
高中数学填空题专练
100、一个容量为 20 的样本数据,分组情况及各组的频数如下:(10,20],2 ;(20,30],3 ;(30,40],4;(40,50],5 ;
(50,60],4; (60,70],2 .则样本数据在(-∞,30)上的概率为________
f (x) lg(2 x x
2 )
101、函数 的定义域是 。
x x
102、已知一个等比数列的前三项的积为 3,后三项的积为 9,且所有项的积为 243,则该数列的项数
为 。
103、已知定义在 R 上的偶函数 f(x)在[0,+∞)上是增函数,且 f(2)=1,若 f(x+a) ≤1 对 x∈[-1,1]恒成立,则
实数 a 的取值范围是 。
104、 2已知抛物线 y 2px 2的准线与双曲线 x y2 2 的左准线重合,则 p的值为
105、在等比数列{an}中,已知 a1 a
1
2 ,a3 a4 1,则 a7 a8 a9 a10 的值为2
x2 y2
106、已知椭圆的方程为 2 2 1(a b 0) ,过椭圆的右焦点且与 x 轴垂直的直线与椭圆交于 P、Qa b
两点,椭圆的右准线与 x 轴交于点 M,若 PQM 为正三角形,则椭圆的离心率等于
107、已知直线 x+ay=2a+2 与直线 ax+y=a+1 平行,则实数 a 的值为 。
x 1 1 , x [0, )
f (x)
2 2
108、已知函数 若存在 x1, x2 ,当0 x1 x2 2 时, f (x1) f (x2 ) ,则 x1 f (x2 )
2x 1, x 1 [ , 2)
2
的取值范围是
109、从 1,2,3,4,5 这 5 个数中一次随机取两个数,则这两个数的和为 5 的概率为 。
第17页,共66页
高中数学填空题专练
110、 *设数列{x n }满足 log 2 x n 1 1 log 2 x n (n N ) 且 x1 x 2 x10 10,
记{x n }的前 n 项和为Sn ,则S20
111、定义在实数集 R 上的奇函数 f x 满足 f (x) 2x 4(x 0) ,则不等式 f (x 2) 0 的解集是
_________
112、 Rt ABC , C 90 在 中,且 A. B. C所对边分别为 a,b,c,若 a b cx,则实数 x的取
值范围为 __________ .
2
113、 x 2x x关于 的不等式 4的解集为 .
114、 2圆 (x 1) (y 2)2 5 在 y 轴上截得的弦长为 .
115、在区间[-3,5]上随机取一个数 x,则 x [1,3]的概率为_________
116、定义在 R上的 f (x) 2,满足 f (m n ) f (m) 2[ f (n)]2 ,m,n R, 且 f (1) 0,则 f (2012) 的值
为
117、等比数列 an 中, a3 20, a6 160,则 an
118、将正偶数排列如下表其中第 i行第 j个数表示 a (i N * , j N *ij ) ,例
如a32 10,若 a ij 2012 ,
则 i j .
第18页,共66页
高中数学填空题专练
119、 0已知△ABC 中的一个内角为 120 ,并且三边长构成公差为 4 的等差数列,则△ABC 的面积
为 。
120 、 已 知 f (x) 是 定 义 在 R 上 的 不 恒 为 零 的 函 数 , 且 对 任 意 实 数 a 、 b 满 足
n n
f (a b) af (b) bf (a), f (2) 2,a f (2 ) (n N*),b f (2 ) n n n (n N*),有以下结论:n 2
① f (0) f (1) ② f (x) 为偶函数;③数列{an}为等比数列;④数列{bn}为等差数列。其中正确结
论的序号是 。
C
D
A
B
121、若集合 A { 1,0,1} , B {x | 0 x 2},则 A B ______ _____.
122、函数 f (x) 2 sin(2x ) 2 的最小正周期是 .
3
5i
123、复数 的实部是_________;
1 2i
第19页,共66页
高中数学填空题专练
4 3
124、已知正三棱锥的底面边长为 2,侧棱长为 3 ,则它的体积为 。
125、在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 .
甲 乙
8 2 9
9 1 3 4 5
2 5 4 8 2 6
7 8 5 5 3 5
6 6 7
2
126、函数 f x sin x cos x 的单调递增区间是 。
127、如果执行如图的流程图,那么输出的 S .
开始
S 0,i 1
i≤10 N
否
Y
S 输出 S
i i 2
结束
第 7 题
第20页,共66页
高中数学填空题专练
x 3,
128、由不等式组 y 0, 所确定的平面区域的面积等于__________;
y x 1,
129、已知向量 a,b满足 | a | 1,| b | 2,a (a b) ,则向量a,b夹角的大小为 .
130、如果底面直径和高相等的圆柱的侧面积是π,则这个圆柱的体积是 .
131、 p x [ 0,1] k 4 x k 2 x 1已知命题 :对一切 , 6(k 5) 0 ,若命题 p是假命题,
则实数 k的取值范围是 .
132、已知集合 A={1,2},B={-1,0,1},则 A∪B= 。
133、过点(1,0)且与直线 x 2y 2 0平行的直线方程是 .
A x Z x2 5x 0 B x x 4 0 (C A) B
134、已知全集U R,集合 , 则 U 中最
大的元素是 ▲ .
135、 如图,⊙O中,直径 AB 和弦 DE 互相垂直,C 是 DE 延长线上一点,连结 BC 与圆 0 交于 F,
若∠CFE= ( (0, ) ),则∠DEB___________
2
第21页,共66页
高中数学填空题专练
x 1136、 n已知( ) 展开式的第 4项为常数项,则展开式中各项系数的和为________
2 3 x
137、 2已知数列{an}的前 n 项和 Sn=n -7n,且满足 16 x 3 cos
138、设点 A,B 分别在曲线 C1 : ( 为参数)和曲线 C2 : 1上,则 |AB|的最小值
y sin
为 。
139、设向量 a (cos , 1),b (1, 3cos ) ,且 a //b,则 cos2 = .
140、关于 x的不等式 | x 2 | | x a | 2a在 R上恒成立,则实数 a的最大值是 .
141、将函数 y sin x( 0)的图象向左平移 个
6
单位后的图象如图所示,则平移后的图象所
对应的函数的解析式是 。
y
1
7
12
0 x
-1
第22页,共66页
高中数学填空题专练
142、从一个棱长为 1的正方体中切去一部分,得到一个几何体,其三视图如右图,则该几何体的体积为
______________
143、已知m (cos x, sin x)( 0),n (1, 3),若函数 f (x) m n的最小正周期是 2,
则 f (1) ▲ .
144、已知函数 f (x)
x (0, )
1 2x tan x, 2 ,则 f (x) 的单调减区间是 ▲ .
145、P 为抛物线 y
2 4x上任意一点,P 在 y 轴上的射影为 Q,点 M(4,5),则 PQ 与 PM 长度之和的
最小值为: ▲ .
x y 2 0
y 2 0
x y 2 0 2 2146、过平面区域 内一点 P作圆O : x y 1的两条切线,切点分别为 A,B,
记 APB ,则当 最小时cos ▲ .
第23页,共66页
高中数学填空题专练
147、如图所示的数阵叫“莱布尼兹调和三角形”,他们是由整数的倒数组成的,第 n行有 n个
1 (n 2)
数且两端的数均为 n ,每个数是它下一行左右相邻两数的和,
1 1 1 1 1 1 1 1 1
, ,
如:1 2 2 2 3 6 3 4 12 …,则第 n(n 3) 行第 3 个数字是 ▲ .
k k 1MB MD
148、已知正方形 ABCD的坐标分别是 ( 1,0) , (0,1) , (1,0), (0, 1) ,动点 M 满足: 2 则
MA MC ▲ .
149、若过定点M ( 1, 0)且斜率为 k 的直线与圆 (x 2)2 y 2 9 在第一象限内的部分有
交点,则 k 的取值范围是 。
150、在平面几何里,有:“若 ABC的三边长分别为 a,b,c, 内切圆半径为 r ,则三角形面积为
S 1 ABC (a b c)r ”,拓展到空间,类比上述结论,“若四面体 A BCD的四个面的面积分别为2
S1,S2 ,S3 ,S4 ,内切球的半径为 r,则四面体的体积为 ”
151、 2设斜率为 2 的直线 l过抛物线 y ax(a 0) 的焦点 F,且和 y 轴交于点 A,若 OAF (O 为坐标原
点)的面积为 4,则抛物线方程为 。
152、已知如下算法语句
输入 t;
If t<5 Then
y=t2+1;
Else
if t<8 Then
第24页,共66页
高中数学填空题专练
y=2t-1;
Else
y= 8t 1 ;
End If
End if
输出 y
若输入 t=8,则下列程序执行后输出的结果是 .
2x 1(x 1)
153、已知 f (x) 则f [ f ( )]
sin x 2(x 1)
y 1,
154、若实数 x,y满足 y 2x 1,如果目标函数 z x y的最小值 1,则实数 m= 。
x y m.
155、已知关于 x的不等式: 2x m 1的整数解有且仅有一个值为 2.则整数m的值为____________.
3 2
156、不等式 的解集为
x x 1
1
157、若不等式 2a 1 x x 对一切非零实数 x恒成立,则实数 a的取值范围
158、已知 ABC的内角 A,B,C 所对的边分别为 a,b,c,且 a 2,b 3, cosB 4 .
5
则 sin A的值为 .
ABC cos( A) : sin B : cos(3 159、在 中,若 C) 3 : 2 : 4 ,则 cosC的值为
2 2
160、从甲、乙等 5 人中选出 3 人排成一排,则甲不在排头的排法种数是 (用数字作答)
第25页,共66页
高中数学填空题专练
x y 2
161、已知实数,x,y 满足约束条件 y x 2 ,则 z=2x+y的最小值是____
y 1
1 4
162、已知 a,b,c>0 且 a+2b+c=1,则 的最小值为
a b b c
(二)选考题(请考生在第 15、16 两题中任选一题作答,请先在答题卡指定位置将你所选的题目序号后
的方框用 2B 铅笔涂黑. 如果全选,则按第 15 题作答结果计分.)
10 10 1
163、已知 xi>0(i=1,2,3,…10.),且 xi=1. 则 T= 的最小值为
i 1 i 1 x i
� 164、 如图,PA是圆O的切线,A是切点,直线 PO交圆O于 B、C 两点,D是OC的中点,连结 AD
并延长交圆O于点 E,若 PA 2 3 ,∠ APB 30 ,则 AE ________.
�A
�P �D
�B �O �C
�E
165、某种产品的广告费支出 x与销售额 y之间有如下对应数据(单位:百万元).
x 2 4 5 6 8
y 30 40 60 t 70
根据上表提供的数据,求出 y关于 x的线性回归方程为=6.5x+17.5,则表中 t的值为 .
166、设等差数列{an}的前 n项和为 Sn,若 a2 a5 a8 15,则 S9 = .
167、二项式 ( x 2 10
x2
) 展开式中的常数项是 .
第26页,共66页
高中数学填空题专练
f (x) D , f (x) D , a,b168、 D f (x) a,b, 函数 的定义域为 若满足① 在 内是单调函数 ②存在 使 在 上的
b, a
值域为 ,那么 y f (x) 叫做对称函数 ,现有 f(x) 2 x k是对称函数 , 那么 k 的取值范围是
▲ .
169、在边长为 2 的正三角形 ABC 中,以 A 为圆心, 3 为半径画一弧,分别交 AB,AC 于 D,E.若在△ABC
这一平面区域内任丢一粒豆子,则豆子落在扇形 ADE 内的概率是________.
sin( ) sin( )
170、已知 tan 2 ,则 2 的值为 .
cos(3 ) cos( )
2
171、如右图所示,一个三棱锥的三视图是三个直角三角形 (单位:cm),则该三棱锥的外接球的表面积为
__________cm2.
172、设 f (x) 是定义在R上的偶函数,对任意 x R,都有 f (2 x) f (x 2)成立,且当 x [ 2,0]时,
x
f (x) 1 1.若关于 x的方程 f (x) log a(x 2) 0 (a 1)在区间 (0,6]内恰有两个不同实根,则实
2
数 a的取值范围是 .
173、 (1 x)(1 x)5展开式中x 4 的系数是 (用数字作答).
第27页,共66页
高中数学填空题专练
174、设互不相同的直线 l,m,n 和平面α、 、 ,给出下列三个命题:
①若 l与 m 为异面直线, l ,m ,则α∥
②若α∥ , l ,m ,,则 l∥m;
③若 l, m, n, l∥ ,则 m∥n.
其中真命题的个数为______
175、定义:对于映射 f : A B,如果 A 中的不同元素有不同的象,且 B 中的每一个元素都有原象,则
称 f : A B为一一映射.如果存在对应关系 ,使 A到 B成为一一映射,则称 A和 B具有相同的势.给
出下列命题:
①A={奇数},B={偶数},则 A和 B 具有相同的势;
②A是直角坐标系平面内所有点形成的集合,B是复数集,则 A和 B 不具有相同的势;
③若 A= a,b ,其中 a,b是不共线向量,B= c | c与a,b共面的任意向量 ,则 A和 B不可能具有相
同的势;
④若区间 A= -1,1 ,B= , ,则 A和 B具有相同的势.
其中真命题为
3
176、设α为△ABC 的内角,且 tanα=- ,则 sin2α的值为____
4
lg(x 1) x 1
1
177、若函数 y=f(x)(x∈R)满足 f(x-2)=f(x),且 x [ 1,1]时,f(x)=1-|x|,函数 g(x) x 0 ,则方
x
0 0 x 1
程 f(x)-g(x)=0 在区间[-5,6]内的解的个数为_______.
178、集合 A x | x2 9 0 ,集合 B x | x 1x 2 0 ,则 A B =_ _.
179、下列图形中,若黑色三角形的个数依次构成一个数列的前 4 项,则这个数列的一个通项公式为 an
第28页,共66页
高中数学填空题专练
n N * .
a x
180、已知函数 f(x)的定义域为 D,[a,b]为包含于 D的任意一个区间,若对任意的 x0∈(a,b),m 0 ,
2
x b
n 0 ,都有 | f (m) f (n) | | f (a) f (b) | ,则称 f(x)为 函数.
2
那么下列函数中, 函数有 .(请填上你认为正确命题的所有序号)
① f (x) 2 sin(x ) ; ② f (x) 2 x 1 ;
4
③ f (x) 1 x3 x2 3x 2 ; ④ f (x) ln (x 1) ,
3
181、若 f x 是 R上的奇函数,则函数 y f x+1 -2的图象必过定点 .
2 2
182、已知 F1,F
x y
2 分别是双曲线 2 2 1 a 0,b 0 的左、右焦点,以 F1F2 为直径的圆a b
与双曲线在第一象限的交点为P,则当 PF1F2 的面积等于 a2 时,双曲线的离心率为 .
x t 4cos
183、在曲线 为参数 上,仅存在四个点到点 1,0 距离与到直线 x 1的距离相等,
y 4sin
则 t的取值范围是
184、定义: S为 R的真子集, x, y S,若 x y S , x y S,则称 S对加减法封闭。
有以下四个命题,请判断真假:
①自然数集对加减法封闭;②有理数集对加减法封闭;
③若有理数集对加减法封闭,则无理数集也对加减法封闭;
④若 S1,S2为 R的两个真子集,且对加减法封闭,则必存在 c R,使得 c S1 S2 ;
四个命题中为“真”的是 ;(填写序号)
第29页,共66页
高中数学填空题专练
185、已知 AD是 ABC的中线,若 A 120 , AB AC 2,
则 AD 的最小值是__________ .
1
186、 2 8(1+2x )(x- ) 的展开式中常数项是________(用数字作答);
x
x 0,
187、已知 x、y 满足约束条件 y 0, 则z x 2y的最小值
x y 2,
为 .
1
188、 ! *已知 an=错误 ,数列{ }的前 n 项和为 Sn,bn=n-33,n∈N ,则 bnSn的最小值为__________.
an
189、 3 2 3对任意的实数 x,有 x a0 a1 (x 2) a2 (x 2) a3 (x 2) ,则 a2的值是 。
190、若点 P(cos ,sin ) 在直线 y 2x上,则 sin 2 2cos 2 = .
191、若某程序框图如图所示,则该程序运行后输出的 s .
第30页,共66页
高中数学填空题专练
192、设有算法如图:如果输入 A=144, B=39,则输出的结果是 .
开始
输入非零正整数 A,B
是
B=0? 输出 A 结束
否
C=A 除以 B 的余数
A=B
B=C
1 a 1
193、若二项式 (a x )6 的展开式中的常数项为 160 ,则 ( x )dx = .x 1 x
194、一个总体分为 A,B两层,其个体数之比为 4 :1,用分层抽样法从总体中抽取一个容量为 10 的样本,
1
已知 B层中甲、乙都被抽到的概率为 ,则总体中的个体数是 .
28
第31页,共66页
高中数学填空题专练
195、选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
A.(选修 4—4 坐标系与参数方程)已知点 A 是曲线 2sin 上任意一点,则点 A 到直线
sin( ) 4的距离的最小值是 .
3
B.(选修 4—5 不等式选讲)不等式 | x log 2 x | x | log 2 x | 的解集是 .
C.(选修 4—1 几何证明选讲)如右图所示, AC和
AB分别是圆O的切线,且OC 3, AB 4 ,延长
AO到D点,则 ABD的面积是 .
196、已知集合 A {x x 2},B {x ln(x 1) 0},则 A B = .
197、某算法流程图如图所示,则输出的结果是 .
198、已知一个四棱锥的三视图如图所示,则该四棱锥的体积是 ______ .
第32页,共66页
高中数学填空题专练
1 1
2 2
主视图 左视图
2
俯视图
x y 2
199、已知 O 是坐标原点,点 A(-1,-2),若点 M(x,y)平面区域 x 1 上的一个动点,使
y 2
OA (OA MA) 1 0恒成立,则实数 m 的取值范围为_____________.
m
200、如图是 2012 年某高校自主招生面试环节中,7 位评委对某考生打出的分 数茎叶统计图.去掉一个最
高分和一个最低分后,所剩数据的平均数为____,方差为____.
1
201、在等差数列{an}中,若 a9=6 则 a7 a3 = .3
202、如图,曲线 OB 2的方程为 y x(0≤x≤1),为估计阴影部
分的面积,采用随机模拟方式产生菇∈(0,1),y∈(0,1)的
200 个点(x,y),经统计,落在阴影部分的点共 134 个,则估
计阴影部分的面积是 .
第33页,共66页
高中数学填空题专练
203、一个几何体的三视图如图所示,其中正视图是腰长为 2 的等
腰三角形,俯视图是半径为 1 的半圆,则该几何体的表面积
是 .
204、若二项式 (3x2 1 )n 的展开式中各项系数的和是 64,则展开式中的常数项为 .
x
1 2
205、 2已知随机变量 服从正态分布 N (1, ) ,P( m) ,P( m 1) ,则实数m ___________.
3 3
x 3y 5 0
206、已知变量 x, y 满足 2x y 0 ,则 z log2 x log2 y 1 的最大值为_____.
x 0, y 0
第34页,共66页
高中数学填空题专练
y ln( x
2 2x 3)
207、函数 的定义域为 。
x 1
x 3y 5 0
208、 已知变量 x, y满足 2x y 0 ,则 z log2(2x y) 的最大值为__________.
x 0, y 0
209、 3 2对于三次函数 f (x) ax bx cx d( a 0),定义:设 f (x)是函数 y=f(x)的导数 y= f (x)
的导数,若方程 f (x)=0 有实数解 x0,则称点(x0,f(x0))为函数 y=f(x)的“拐点”.有同学发现“任何
一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”
3 1
请你将这一发现为条件,函数 f (x) x3 x2 3x ,则它的对称中心为 ;
2 4
1
计算 f ( ) 2 f ( ) f ( 3 ) 2012 f ( ) = .
2013 2013 2013 2013
(二)选做题(14-15题,考生只能从中选做一题. 两题都答的按第 14题正误给分.)
5
210、 a x 1 x 的展开式中 x2 项的系数是 15,则展开式的所有项系数的和是_______
211、如图,⊙O1与⊙O2相交于 A、B 两点,过点 A 作⊙O1的切线交⊙O2于点 C,过点 B 作两圆的割线,分
别交⊙O1、⊙O2于点 D、E,DE 与 AC 相交于点 P.若 AD 是⊙O2的切线,且 PA=6,PC =2,BD =9,则 AD 的
长为________。
212、某校高三年级共 1500 人,其中高三(2)班学生人数为 60 人.学校为了检查同学们的健康状况,随
机抽取了高三年级的 100 名同学作为样本,测量他们的体重(单位:公斤),体重的分组区间为[40,45),
[45,50),[50,55),(55,60),[60,65],由此得到样本的频率分布直方图,如图 3.根据频率分布直
方图,估计该校体重低于 50 公斤的人数为_________;若用分层抽样方法,则高三(2)班应抽取
_________人.
第35页,共66页
高中数学填空题专练
213、(坐标系与参数方程选做题)在极坐标系中,直线 l经过圆 2cos
的圆心且与直线 cos 3平行,则直线 l与极轴的交点的极坐标
为_________.
n,n为奇数
214、 *已知数列 an 的递推公式 an a ,n为偶数(n N ) ,则 a24 a25 ;数列 an
n 2
中第 8 个 5 是该数列的第 项.
215、 f (x) ax3 bx 2对于三次函数 cx d( a 0),定义:设 f (x)是函数 y=f(x)的导数 y= f (x)
的导数,若方程 f (x)=0 有实数解 x0,则称点(x0,f(x0))为函数 y=f(x)的“拐点”.有同学发现“任何
一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”
3 1
请你将这一发现为条件,函数 f (x) x3 x2 3x ,则它的对称中心为 ;
2 4
计算 f ( 1 ) f ( 2 ) f ( 3 ) 2012 f ( ) = .
2013 2013 2013 2013
216、连掷两次骰子得到的点数分别为m,n.记向量 a (m,n) 与向量b (1, 1)的夹角为 ,则 (0, ]
2
的概率是_______________.
217、在某次测量中,测量结果 服从正态分布 N(1, 2 ) ,
若 在(0,1)内取值的概率 0.35, 则 在(0,2)内取值的概率为________.
218、已知有公共焦点的椭圆与双曲线中心为原点,焦点在 x轴上,左右焦点分别为 F1,F2 ,且它们在第一
象限的交点为P, PF1F2 是以 PF1为底边的等腰三角形.若 PF1 10 ,双曲线的离心率的取值范围为 (1, 2).则
该椭圆的离心率的取值范围是 .
第36页,共66页
高中数学填空题专练
2
219、记 (x )n 的展开式中第 k 项的系数为 ak ,若a3 5a3 ,则n = _________x
220、 设双曲线的一个焦点为 F,虚轴的一个端点为 B,如果直线 FB 与该双曲线的一条渐近线垂直,那
么双曲线的离心率是_________
a i
221、已知 a R,且 为纯虚数,则 a 。
1 i
222、平面上有一组平行线,且相邻平行线间的距离为 3cm,把一枚半径为 1cm 的硬币任意平掷在这个平
面上,则硬币不与任何一条平行线相碰的概率为 。
223、若直线 y x b与圆 x2 y2 2相切,则 b的值为 。
a i
224、设 i 为虚数单位,若 为实数,则实数 a 的值为 .
1 i
225、已知等差数列{an}的前 n项和为 Sn,若 a3 a6 10,则 S8 的值为________.
226、(极坐标与参数方程选做题)极坐标系下,圆 2cos( )上的点与直线 sin( ) 2 的
2 4
最大距离是 .
227、如图是长方体截去一个角后的多面体的三
视图,则这个多面体的体积为 .
6
3
正视图 侧视图
4
第37页,共66页
俯视图
高中数学填空题专练
228、已知集合M {1, 2,3, ,n}(n N ),若集合 A {a1,a2 ,a3 , ,am} M (m N
) ,且对任意的 b M ,存
在 ai ,a j A(1 i j m),使得 b = 1ai + 2a j(其中 1, 2 { 1,0,1}),则称集合 A为集合M 的一个m -
生成元.若集合 A为集合M = {1, 2,3, ,8}的一个m - 生成元,则m的最小可能值为 .
229、为调查学生的身高与饮食习惯的关系,某中学将
高三同学的身高(单位:厘米)数据绘制成频率分布
直方图(如图).现采用分层抽样的方法从中选取 40
名进行调查,则身高在 [160,170]内的学生中应选取的
人数为 .
2 2
230、若抛物线 y2 8x x y的焦点到双曲线 2 2 1(a 0,b 0) 一条渐近线的距离为 2 ,则双曲a b
线的离心率为 .
x
shx e e
x
chx e
x e x
231、定义“ , x R”为双曲正弦函数,“ , x R”为双曲
2 2
余弦函数,它们与正、余弦函数有某些类似的性质,如:sh(x y) shx chy chx shy 、(chx)2 (shx)2 1
等.请你再写出一个类似的性质: ch(x y) .
第38页,共66页
高中数学填空题专练
2i
232、复数 Z 的虚部是
1 i
233、某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这
些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规
律相同),设第n个图形包含 f (n) 个小正方形,则 f (6) 。
2
234、 在平面直角坐标系 xOy中,椭圆 C的中心为原点,焦点 F1, F2 在 x轴上,离心率为 .过 F1的
2
直线 l交 C于 A,B两点,且△ABF2 的周长为 16,那么 C的方程为________
235、数列 an 的前 n项和为 Sn,若数列 an 的各项按如下规律排列:
1 , 1 , 2 , 1 , 2 , 3 , 1 , 2 , 3 , 4 ,..., 1 , 2 ,... n 1,...有如下运算和结论:
2 3 3 4 4 4 5 5 5 5 n n n
a 3① 23 ;8
②数列 a1,a2 a3 ,a4 a5 a6 ,a7 a8 a9 a10 ,... 是等比数列;
2
③数列 a1,a2 a3 ,a
n n
4 a5 a6 ,a7 a8 a9 a10 ,... 的前 n项和为Tn ;4
④若存在正整数 k,使 Sk 10, S
5
k 1 10 ,则 ak .7
以上所.有.正确结论的序号是 .
236、在如图所示的茎叶图中,乙组数据的中位数
是 ;若从甲、乙两组数据中分别去掉一个最大
数和一个最小数后,两组数据的平均数中较大的
第39页,共66页
高中数学填空题专练
一组是 组.
甲 乙
0 7 9
5 4 5 5 1 8 4 4 6 4 7
m 9 3
237、某工厂经过技术改造后,生产某种产品的产量 x (吨)与相应的生产能耗 y (吨标准煤) 有如下几
组样本数据:
x 3 4 5 6
y 2.5 3 4 4.5
根据相关性检验,这种样本数据具有线性相关关系,通过线性回归分析,求得回归直线的斜率为 0.7,
那么这组样本数据的回归直线方程是________________.
x2 16y2
238、双曲线 12 ( p 0) 的左焦点在抛物线 y2 2px 的准线上,则该双曲线的离心率3 p
为 .
239、某几何体的三视图,其中正视图是腰长为 2的等腰三角形,侧视图是半径为 1 的半圆,则该几何体的
表面积是 .
240、 某班级有 50 名学生,现要采取系统抽样的方法在这 50 名学生中抽出 10 名学生,将这 50 名学生
随机编号 1—50 号,并分组,第一组 1—5 号,第二组 6—10 号,……,第十组 46—50 号,若在第三组中
抽得号码为 12 的学生,则在第八组中抽得号码为___ 的学生.
第40页,共66页
高中数学填空题专练
�
241、 f (x) = 1+ x
2 + 1+ (1- x)2 (0#x 1)
某同学为研究函数 的性质,构造了如图所示的两个边
长为 1 的正方形 ABCD和 BEFC,点 P是边 BC上的一个动点,设CP = x,则 AP + PF = f (x) .
请你参考这些信息,推知函数 f (x) 的图象的对称轴是 ;函数 g(x) = 4 f (x)- 9的零点的个数
是
D C F
P
A B E
242、已知向量 a、b 的夹角为60 ,|a|=2, |b|=3,则|2a-b |= .
243、如图所示:有三根针和套在一根针上的 n 个金属片,按下列规则,把金属片从一根针上全部移到另
一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的
金属片上面.将 n 个金属片从 1 号针移到 3 号针最少需要移
动的次数记为 f (n);
则:(Ⅰ) f (3) (Ⅱ) f (n)
第 17 题图
244、 函数
(1)若 a=0,则方程 f(x)=0 的解为_______.
第41页,共66页
高中数学填空题专练
(2)若函数 f(x)有两个零点,则 a 的取值范围是_______.
245、命题“ x0 (0, ), tan x sin x ”的否定是 .2 0 0
246、已知△ ABC中, AD BC于D, AD BD 2 ,CD 1,则 AB AC ___.
247、设抛物线的顶点在原点,其焦点 F 在 y轴上,抛物线上的点 P(k, 2) 与点 F 的距离为 4,则抛物线方
程为 .
248、等比数列 an 的前 n项和为 Sn,已知 S1 ,2S2 ,3S3 成等差数列,则 an 的公比为 .
249、已知某算法的流程图如图所示,若将输出的 (x, y) 值依次记为
(x1 , y1), (x2 , y2 ) , , (xn , yn ), .
(1)若程序运行中输出的一个数组是 (t, 8) ,则 t ;
( 2)程序结束时,共输出 (x, y) 的组数为 .
第42页,共66页
高中数学填空题专练
x, x 0
250、. 已知 f x x, x 0 ,则不等式 x x f x 2的解集是_________.
2x y 6 0
251、 设不等式组 x y 3 0 所表示的平面区域为M ,若函数 y k x 1 1的图像经过区域M ,
y 2
则实数 k的取值范围是_________.
252、 2若集合 M= 1,m ,集合 N= 2,4 ,M N 1,2,4 ,则实数m的值的个数是_________
253、已知数列 an 的前 n项和 S n 2n 7n,且满足16 ak ak 1 22 ,则正整数 k _____
3
x t 2
254、(极坐标与参数方程)已知曲线 C的极坐标方程是 2sin ,直线 l 的参数方程是 5 (t
y 4 t 5
为参数).设直线 l与 x轴的交点是 M,N 是曲线 C 上一动点,则 MN 的最大值为____________
1
255、 f (x) 1 ( ) x函数 的定义域是 .
2
第43页,共66页
高中数学填空题专练
256、 a= (x 1,2), b = (4, y) , a b 9 x 3 y已知向量 若 ,则 的最小值为 .
257、在等比数列{an}中,若 a3 ,a
2
9 是方程3x 11x 9 0的两根,则 a6 的值是 .
(二)选择题(14-15 题,考生只能从中选做一题。两题都答的按第 14 题正误给分。)
258、曲线 y x3与直线 x 1及 x轴所围成的图形的面积为 .
259、从圆 O外一点 A 引圆的切线 AD和割线 ABC,已知 AD=4,AC=8,圆 O半径为 5,则圆心 O到直
线 AC的距离为 。
x t cos x 4 2cos
260、直线 (t为参数),与圆 ( 为参数)相切,则此直线的倾斜角
y t sin y 2sin
= .
261、 如图,在△ ABC中,D是边 AC上的点,且 AB AD, 2AB 3BD,BC 2BD,
则 sinC的值为 .
262、一个六棱柱的底面是正六边形,其侧棱垂直于底面.已知该六棱柱的顶点都在同一个球面上,且这
4
个球的体积为 ,已知该六棱柱的高为 3 ,则这个六棱柱的体积为 。
3
第44页,共66页
高中数学填空题专练
263、已知△ ABC为锐角三角形,若 A 2B a,则 的取值范围是 。
b
264、如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数
之和是 _________ .
甲 乙
53 41 5
368 2 6 3 7 8
2
479 3 57
1 4
x 2y 1 0,
265、已知实数 x,y 满足 且 z 3x y的最大值是 。
| x | y 1 0
1
266、若不等式 | x | | a 2 | 1对一切非零实数 x均成立,则实数 a的取值范围是 __________ .
x
267、点 M,N分别是曲线 sin 2和 2cos 上的动点,则|MN|的最小值是 .
以下是答案
一、填空题
1、 ①④
2、196
3、内角平分线
4、
5、
第45页,共66页
高中数学填空题专练
6、 2
7、【答案】 3 1
【解析】解:设正六边形的边长为 2c,则焦距为 2c,连接 EA,ED,则在三角形 EAD 中,
|EA|+|ED|=2a,DE AE DE 2 AE 2 AD2 ,DE 1 AD ,解得
2
AE 3c, 3c c 2a, e 3 1,故答案为 3 1
8、 4
9、3
10、 k ,k (k Z ) 4 4
3
11、
2
19
12、
6
13、-20【解析】
14、-3【解析】 f (x)是奇函数, f (1) f ( 1) [2 1} 3
15、D
16、
17、 700
1
18、
7
19、 4
20、2
第46页,共66页
高中数学填空题专练
21、72
22、11
23、2
24、
25、
26、
27、
28、
29、
30、
31、
32、答案: k 8
第47页,共66页
高中数学填空题专练
解析: n 1时, a1 S1 1 9 8,当n 2时,an Sn Sn 1 n
2 9n (n 1)2 9(n 1)
2n 10 , n 1时适合此式, an 2n 10 ,5 2k 10 8,7.5 k 9,又k N k 8
33、
34、
35、C 0 1 2 3n Cn Cn Cn
1
36、 ( ,1]
2
37、
38、 31
39、
40、 答案:原点
1
解析:由 lga+lgb=0 ab=1 b g x x= ,所以 ( )=- a ,故 f(x)与 g(x)关于原点对称.
a
41、
42、 【答案】10 年
1000 a b a 500
【解析】 y 500x2 bx.
3000 4a 2b b 500
M 50000 6000 500x 50000 500 500x 6500 16500.
年均消耗费用 x x
当x 10时,M最小.
第48页,共66页
高中数学填空题专练
所以使用 10 年最佳.
43、
三,解答题:
44、 1 i
45、 ①②
46、 684
3
47、
4
48、 3
49、 -1
50、 3a2答案: 10ab 3b2 4 0
解析:该题综合考查直线与圆锥曲线的位置关系,向量线性表示及坐标运算.可求出 e1 (1,1),e2 (1, 1) ,
a b x 2
设 P(x , y ) 0 (a b)0 0 ,则 , (a b)
2 1,
a b y0 4
3a2 10ab 3b2 4 0
9
51、 答案:
5
解析: sin y x , cos , 直线l的方程为3y-4x=2
即4x 3y 2 0,点 ( 2, )为 (1, 1),d (4 3 2) 9
4 42 ( 3)2 5
52、 答案:300
解析:连结OC,则OC OD, AD CD, OC / /AD, DAC OCA
BC 3 1 AB, CAB 300 ,又 OC OA, OCA 300 , DAC 300
2
第49页,共66页
高中数学填空题专练
53、答案:[2, ) {0}
解析:该题考查函数性质以及解二次不等式和解不等式组,容易产生漏解.
54、答案:i
解析:该题考查复数的运算及其概念,属于简单题.
55、答案:必要不充分条件.
解析:考查集合及其运算以及简易逻辑,是简单题.
56、答案:3
解析:该题考查抽样方法、总体分布的估计、总体特征数的估计.由
(0.005+0.010+0.020+0.035+a) 10=1得 a 0.030 ,因此, [120,130﹚,[130,140﹚,[140,150]三
组学生人数分别为:0.3 100 30,0.20 100 20,0.10 100 10,所以, 从身高在[140,150]内的学生
10
中选取的人数应为 18 3
30 20 10
57、 x y 1 0
58、 答案: (2, )
解析:该题考查对数函数及其性质,还有基本不等式;因为函数 f (x) | lg x |.若 f (a) f (b)且 a b ,所
以, lgb lg a , ab 1, a b a
1
2
a
6
59、
5
60、
15
61、 【答案】
4
第50页,共66页
高中数学填空题专练
【解析】
4
log 273 lg 25 2lg 2 e
ln 2
3
1
log 43 3 2(lg5 lg 2) 2
1
2 2
4
15
.
4
62、 【答案】 1或 2
【解析】因为 y f (x) 在 (0, )上是减函数,所以
n2 3n 0, 0 n 3, n Z n 1或2. 符合偶函数.
7
63、 【答案】 ( ,5)
4
2
【解析】设函数 f (x) 3tx (3 7t)x 4, 则满足0 1 2的条件为:
f (1) 0 7 4t 0
f (2) 0 即 10 2t
7
0 t 5. [
4
f (0) 0 4 0
64、 【答案】2
x y
【 解 析 】 因 为 直 线 FB 方 程 为 1,bx cy bc 0, 右 顶 点 A(a,0) ,
c b
b ab bc 4
8a2 14ac 5c2 0, 5e2 14e 8 0,e 2或 (舍去).
7 b2 c2 5
65、80
1
66、 答案: ( , ]
4
2 2
解析: 该题考查直线与圆的位置关系和二次函数的性质;因为圆 x y 2x 4y 1 0关于直线 2ax-
1
by+2=0(a,b∈R)对称,所以,点 ( 1,2) 在直线 2ax-by+2=0 上,所以,a+b=1,ab a(1 a)
4
3
67、π+
3
第51页,共66页
高中数学填空题专练
68、①、④
69、
800, 20%
70、 3
71、b c a;
3
72、 ;
5
y 2 x 2
73、
b 2
b 4
1
a 2
74、1
75、 ① ③ ④
三解答题:
76、7;
77、 a 2 ;
78、 2 2 3
79、13
80、 ( 1 , 3)
2 2
1
81、[ ,1]
2
82、(1)(2)(4);
83、答案:2
第52页,共66页
高中数学填空题专练
m2 m 1 1
解析:只要根据幂函数的定义及性质即可得出 m 2 ,学生在幂函数概念方面容易出2
m m 3 0
错,;考查幂函数概念与性质、函数性质,是中档题。
1
84、 -
2
85、1
86、 3x 4y 20 0
87、③
88、9
89、10
n 1
90、数列{n Tn} 为等比数列,且通项为 n Tn b1q 2 ;
91、M=8
92、 2 ;
93、 答案:2
解析: 该题 f (x) g(x) m且 g(x) 是奇函数的形式的函数,但是不注意又不易看出,增加做题的难度,既
考查函数性质又转化化归能力,是中档题。
f (x) | x | sin x 1 sin x
sin x
因为 1而 是奇函数,所以, M m 2
| x | 1 | x | 1 | x | 1
94、
第53页,共66页
高中数学填空题专练
n(n 1)
95、
2
3 7
96、
2
97、 21
98、答案:[1, )
解析:由 A {x | y x 1},B {y | y x2 1}简单考查函数的定义域与值域,由 A B考查集合
的交运算, A [ 1, ),B [1, ), A B [1, ) 。属于简单题。
99、
1
100、
4
101、(-1,0)
102、10;
103、[ 1,1]
第54页,共66页
高中数学填空题专练
104、2 ;
105、12;
3
106、 ;
3
107、1;
108、 [2 2 , 1) .
4 2
1
109、 5
110、 10250
111、 [ 4, 2] [0, )
112、 1,, 2
三解答题
113、 2,1
114、4
1
115、 .
4
116、1006;
117、5 2n 1
118、62
119、答案: 15 3
解析:由题意可以设三边长分别为:a-4,a,a+4,则由余弦定理得:
(a 4)2 a2 (a 4)2 2a(a 4)cos120 , a 10, 由正弦定理面积公式得:
第55页,共66页
高中数学填空题专练
S 1 a(a 4)sin120 15 3 。这是今年的一道高考题,综合考查等差数列概念,正余弦定理,是中档
2
题。
120、答案: ①③④
解 析 : 因 为 a,b R, f (a b) af (b) bf (a), 取a 1,b 1,得f (1) 0, 取 a=2,b=2, 得
f (4) 4 f (2) 8, 取 a 0,b 2 得 f (0) 2 f (0), f (0) 0, 取 a=-2,b=-2, 得
f (4) 4 f ( 2), f ( 2) 2,取 a 2,b 2n 1, f (2n ) 2 f (2n 1) 2n 1得 f (2)
f (2n ) f (2n 1 n
2 f (2n 1) 2n , ) f (2 ) 1, (1) 由 a (n N*) 得 f (2n ) na 代入(1)得
2n 2n 1 n n n
nan (n 1)an 1 na
n n 1 1, a1 f (2) 2,
n
n n, a
n
n 2 。该题通过函数方程考查函数性质与递推数2 2 2
列求数列通项公式,既考查函数方程问题一般的研究方法:赋值,又考查转化化归,对能力要求较高,是
难题。
121、{0,1}
122、
123、2
2 3
124、 3 ;
125、 45 46
k 126、 ,k
(k Z )
4 4
127、 25
128、 2
第56页,共66页
高中数学填空题专练
129、 120
130、
4
131、 [5, 6]
1,0,1,2
132、 ;
133、 x 2y 1 0
134、3
135、a
1
136、
32
137、8
138、1
1
139、
3
2
140、
3
141、 y sin 2x
3
5
142、
6
第57页,共66页
高中数学填空题专练
143、-1
( , )
144、 4 2
145、 34 1解析:焦点 F (1,0) PM PQ =PM PF 1,而 PM PF的最小值是MF 34
146、 P O P 4, 2 当 离圆 最远时 最小,此时点 坐标为: 记 APO ,
9
则 cos 1 2sin
2 ,计算得 cos =10
147、
2
n (n 1) (n 2) ,
k k 1 y 1 y 1 1 x
2
2
M MB MD
y 1
148、设点 的坐标为 (x, y),∵ 2 ,∴ x x 2 . 整理,得 2 ( x 0),
发现动点 M 的轨迹方程是椭圆,其焦点恰为 A,C 两点,所以MA MC 2 2
149、 0, 5
1
150、VA BCD (S1 S2 S3 S4 )r在四面体 A BCD中,四面体的体积V3 A BCD
可分成四个小三棱锥的
体积之和,而这四个小三棱锥的高都为内接球的半径 r ,底面积分别为 S1 、 S2 、 S3 、 S4 ,因此
V 1A BCD (S1 S2 S3 S4 )r3
151、 y2 8x
t 2 1(t 5)
152、9 y 2t 1(5 t 8) ,t= 8
8t 1(t 8)
3
153、
4
第58页,共66页
高中数学填空题专练
154、 5
m 1
1 2 2 3 m 5
155、4 m 4
m 1 3 m 5
2 3 2
156、 , 0 1 , 3
[ 1157、 , 3]
2 2
2
158、
5
1
159、
4
160、48;
161、-1
162、9
163、100
10
164、 7
7
165、50
166、45
167、180
2 a k a
f (x) 2 x k , 2168、 2 b k b由于 在 上是减函数,所以 关于 x的方程 2 x k x
k 2, 9 , 2 4 在 上有两个不同实根。通过换元结合图象可得
第59页,共66页
高中数学填空题专练
3
169、
6
170、 3;
171、 29 ;
172、 3 4 a 2.
173、-5;
174、 1
175、①③④
176、
177、 9
178、{x | 1 x 2};
179、 3n 1;
180、②④
181、 -1,-2
182、 2
183、 4,5 ;
184、②④
185、1
第60页,共66页
高中数学填空题专练
186、 -42
187、2
70
188、-
3
189、6
190、-2
191、69
192、 3
4 2 2
193、 ln 2
3
194、40
5
195、A.
2
B. (1, )
48
C.
5
196、 x | 0 x 2 ;
197、16;
4
198、 ;
3
199、 , 0 1 ,
3
第61页,共66页
高中数学填空题专练
200、85 ,1.6
201、4
202、
203、
204、 9
205、
206、2
207、(-1,1)
208、2
(1209、 ,1) ; 2012
2
210、1/4
211、12 .部分提示:
212、600;4
213、 (1,0)
214、28,640
1
215、 ( ,1) ; 2012
2
第62页,共66页
高中数学填空题专练
216、
217、0.7
218、 1 , 23 5
219、 6.
5 1
220、 .
2
221、 1
1
222、
3
223、 2
224、
225、 40
3 2
226、 1
2
227、60
228、3
229、14 ;
230、 2 ;
231、 chx chy shx shy.
232、1
233、61
第63页,共66页
高中数学填空题专练
x2. y
2
234、 + =1.
16 8
235、③, ④
236、84 乙
237、 y=0.7x+0.35
2 3
238、 3
239、 2(π 3)
240、 37
1
241、 x = ;2
2
242、 13
243、(1)7
(2)2n 1
5 -1
244、 (1)
2
- 5 5(2) ,
4 4
245、 x (0, ), tan x sin x
2
246、 2 .
247、 x2 8y
第64页,共66页
高中数学填空题专练
1
248、
3
249、(1)81(2)1004
250、 (-∞, 1〕
1 1
251、 , 4 2
252、 4.
253、8
254、 5 1
255、 0,
256、6
257、 3
1
258、
4
259、4
5
260、 或
6 6
6
261、
6
9
262、
8
263、 2, 3
第65页,共66页
高中数学填空题专练
264、 54 解:甲、乙两人得分的中位数之和是 28 26 54 .
1
265、【答案】 ( , )
2
x 2y 1 0,
【解析】作出不等式组 的平面区域, 由线性规划知识得最优解 (3,2) ,故 z 3x y的最
| x | y 1 0
大值为 7
266、【答案】 (1,3)
1
【解析】∵ | x | 2 ,∴ | a 2 | 1 2 ,即 | a 2 | 1,解得1 a 3 .
x
267、1
第66页,共66页
一、填空题
1、设m、n,是两条不同的直线, 、 是两个不同的平面,给出下列四个命题,
①若m⊥n,m⊥ ,n ,则 n // ;
②若 , m,n m,则n 或n ;
③若m , ,则m // ;
④若m n,m ,n ,则 .
其中正确命题的序号是 (把所有正确命题的序号都写上).
2、随机抽取某产品 n件,测得其长度分别为 a1,a2 , ,an ,若n 4,a1 195,a2 197 ,a3 193,
a4 199,则如右图所示的程序框图输出的 S .
开始
输入 n,a1,a2 , ,an
s 0, i 1
i i 1
是
i n s (i 1) s a i
i
否
输出 s
结束
(第 5 题图)
p x
2 y2
3、命题 :已知椭圆 2 2 1(a b 0) ,F1,F2 是椭圆的两个焦点,P为椭圆上的一个动点,过a b
第1页,共66页
高中数学填空题专练
F2作 F1PF2 的外角平分线的垂线,垂足为M ,则OM 的长为定值.类比此命题,在双曲线中也有命题q:
x2 y2
已知双曲线 2 2 1(a b 0), F1, F2 是双曲线的两个焦点, P为双曲线上的一个动点,过 F 作a b 2
F1PF2 的 的垂线,垂足为M ,则OM 的长为定值.
2 2
4、设点 (a,b)在平面区域D (a,b) a 1, b 1 x y中均匀分布出现,则双曲线 2 2 1(a b 0)的离a b
心率 e满足1 e 2 的概率为 .
5、. O 2设点 是 ABC的三边中垂线的交点,且 AC 2AC AB 2 0 ,则 BC AO的范围是 .
6、 0已知向量a,b满足|a|=2,|b|=1,a与b的夹角为60 ,则|a-2b|等于 .
7、 如图,正六边形 ABCDEF 的两个顶点 A、D 为椭圆的两个焦点,
其余 4 个顶点在椭圆上,则该椭圆的离心率是 .
x 2 y 2
2 2 1(a 0,b 0)
2 3
8、 2已知双曲线 a b 的离心率为 3 ,焦距为2c,且2a =3c,双曲线 上一点P满足
PF1 PF2 2(F1、F2为左右焦点),则 | PF1 | | PF2 | .
9、已知复数 z i(i 3)( i是虚数单位),则复数 z的虚部为 .
10、函数 f x sin x cos x 2的单调递增区间是 ;
1 4
11、已知正项等比数列 an 满足 a7 a6 2a5 ,若存在两项 am、an使得 aman 4a1 ,则 的最小m n
值是 ;
第2页,共66页
高中数学填空题专练
12、对于不等式 y ax2 bx c 2来说,它的几何意义是抛物线 y ax bx c内部(即包含焦点的部分),
y x2 3x 3
y x
那么由不等式组 所确定的图形的面积是 。
y 0
x 3
1 1
13、计算 (lg lg 25) 100 2 = .
4
1
(lg 1 lg 25) 100 2 =(-lg4-lg25) 1 (lg 4 lg 25) 10 lg(4 25 ) 10
4 10
lg(102 10 2 10 20
14、设 f (x) 是定义在R上的奇函数,当x≤0时, f (x) = 2x2 x,则 f (1) .
0, 15、 2设 ,则方程 x cos y
2 sin 1所表示的曲线不可能是-------- ( )
2
A.两条直线 B.圆 C.椭圆 D.双曲线
16、小明爸爸开车以80km/h的速度沿着正北方向的公路行驶,小明坐在车里向外观察,在点A处望见电视
0 0
塔P在北偏东30 方向上,15分钟后到点B处望见电视塔在北偏东75 方向上,则汽车在点B时与电视塔P的距
离是 km.
17、用分层抽样的方法从某高中学校学生中抽取一个容量为 55 的样本参加问卷调查,其中高一年级、高
二年级分别抽取 10 人、25 人。若该校高三年级共有学生 400 人,则该校高一和高二年级的学生总数为
人。
, sin 3 tan 18、已知 , ,则 = ——
2 5 4
19、 O 2 2过原点 作圆 x y 6x 8y 20 0的两条切线,设切点分别为 P、Q,则线段 PQ 的长为——
第3页,共66页
高中数学填空题专练
20、如图,从圆O外一点 P引圆O的切线 PA和
割线 PBC,已知PA 2 2 , PC 4,
圆心O到 BC的距离为 3 ,则圆O的
半径为 .
C B P
O
A
21、已知等差数列 an 的前 n项和为 Sn,若 a4 18 a5 ,则 S8 .
22、若把英语单词“ good ”的字母顺序写错了,则可能出现的错误共有 种.
f (x) log x x b(a 0, a 1) 1 123、已知函数 a 且 ,当 a 且3 b 4时,3 2
函数 f (x) 的零点 x0 (n,n 1),n N
*
,则 n .
24、 x x 2不等式 4 2 0的解集为 .
x2 y2
25、已知双曲线 2 1(b 0) 的一条渐近线的倾斜角为 ,则b的值为 。9 b 3
26、已知集合 P (x, y) x y 0 ,Q (x, y) x y 2 ,则Q P .
第4页,共66页
高中数学填空题专练
27、用 3 种不同的颜色给图中的 3 个矩形随机涂色,每个矩形只涂一种颜色,则 3 个矩形中有且仅有两个
矩形颜色相同的概率是 。
2 2
28、在平面直角坐标系 xOy x y中,已知椭圆 2 a b2
1(a b 0) 的右顶点为 A,上顶点为 B,M 为线段
AB o的中点,若 MOA 30 ,则该椭圆的离心率的值为 。
29、已知等比数列 a 2n 的各均为正数,且 a1 2a2 3,a4 4a3a7 ,则数列 an 的通项公式为 。
30、 m R 2 2设 ,已知函数 f (x) x 2mx (1 2m)x 3m 2 ,若曲线 y f (x) 在 x 0处的切线恒
过定点 P,则点 P 的坐标为 。
f (x), f (x) k ,
31、设函数 y f (x) 在 R 内有定义,对于给定的正数 k,定义函数 fk (x) ,若函数
k , f (x) k.
f (x) log3 | x |
1
,则当 k 时,函数 fk (x) 的单调减区间为 。3
32、 2已知数列{ an }的前 n项和 Sn n 9n,若它的第 k项满足5 ak 8,则 k .
15
33、若 z z z 2i( i为虚数单位),则复数 z = 。
4
34、
为 .
35、已知直线上 n 个点最多将直线分成 C 0 1n Cn n 1 段,平面上 n 条直线最多将平面分成
2
C 0n C
1 C 2 n n 2n n 部分(规定:若 k n,则C
k
n 0),则类似地可以推算得到空间里 n个平面最2
第5页,共66页
高中数学填空题专练
多将空间分成 部分
36、已知 AB AC,| AB AC | 2 ,点M 是线段BC上的一点,且 AM (AB AC) 1,则 | AM |的
取值范围是 .
37、 x2经过圆 2x y2 0 的圆心C,且与直线 x y 0垂直的直线方程是 .
38、若 (x 2)5 a x55 a4x
4 a 33x a2x
2 a1x a0 ,则 a1 a2 a3 a4 a5 _______。
2 3
39、甲、乙两人分别独立参加某高校自主招生面试,若甲、乙能通过面试的概率分别是 ,和 ,则面
3 4
试结束后通过的人数 的数学期望 E 是
40、若 lga+lgb=0(a≠1),则函数 f(x)=ax与 g x x( )=-b 的图象关于________对称.
41、某几何体的三视图如下图所示,则该几何体的表面积为___________
42、 汽车的最佳使用年限是使年均消耗费用最低的年限(年均消耗费用=年均成本费用+年均维修
费),设某种汽车的购车的总费用为 50000 元;使用中每年的保险费、养路费及汽油费合计为 6000 元;
x 2前 年的总维修费 y 满足 y ax bx ,已知第一年的总维修费为 1000 元,前两年的总维修费为 3000
元,则这种汽车的最佳使用年限为 年.
第6页,共66页
高中数学填空题专练
ABC BA BC
43、已知在 中, A 120 ,记 ,
CA CB ,
| BA | cos A | BC | cosC |CA | cos A |CB | cosB
则向量 与 夹角的大小为 .
三,解答题:本大题共 5 小题,共 72 分,解答应写出文字说明、证明过程或演算步骤。
44、若 i为虚数单位,则 (1 i)i .
45、若对于定义在 R上的函数 f (x) ,其图象是连续不断的,且存在常数 ( R),使得对任意实数 x都有
f (x + ) + f (x) = 0成立,则称 f (x) 是一个“ —伴随函数”. 有下列关于“ —伴随函数”的结论:
①f (x) =0 是常数函数中唯一个“ —伴随函数”;② f (x) = x2是一个“ —伴随函数”;
1
③ “ —伴随函数”至少有一个零点. 其中不.正.确.的序号是______.2
46、(优选法与试验设计初步) 用 0.618 法寻找实验的最优加入量时,若当前存优范围是[628,774],好点
是 718,则此时要做试验的加入点值是 。
47、定义在 R 上的奇函数 f (x) 满足: x 0时 f (x) 2 x b 则 f (2) = 。
x 3y 7 0
48、 已知 x, y满足 x 1 ,则 z | y x |的最大值为 .
y 1
2cos
x x 2000
49、已知函数 f (x) 3 ,则 f f 2012 .
x 100 x 2000
x 2
50、如图所示,直线 x 2 与双曲线C : y 2 1的渐近线交于 E1 , E2 两点,记OE1 e4 1
,OE2 e2 ,
任取双曲线C上的点 P,若OP ae1 be2 ,则实数 a和b满足的一个等式是_____________.
第7页,共66页
高中数学填空题专练
51、(坐标系与参数方程选做题)在极坐标系中,直线 l的方程为3 sin 4 cos 2,则点( 2, )
4
到直线 l的距离为 .
52、如图4所示,圆O的直径AB=6,C为圆周
上一点, BC 3过C作圆的切线 l,过A作 l的垂线AD,垂足为D,
则∠DAC= .
53、函数 f(x)= x + x(x-2)的定义域是 .
54、若 z(1 i) 1 i ( i是虚数单位),则 z的共轭复数 z =_____________ .
55、设集合 A x | x 1 ,B x | x a ,则“ A B R”是“a=1”的___________条件.(从如下
四个中选一个正确的填写:充要条件、充分不必要条件、必要不充分条件、既不充分也不必要条件)
第8页,共66页
高中数学填空题专练
56、从某小学随机抽取 100 名同学,这些同学身高都不低于 100 厘米,将他们身高(单位:厘米)数据绘
制成频率分布直方图(如右图).现用分层抽样的方法从身高在[120,130﹚,[130,140﹚,[140,150]
三组学生中,选取 18 人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
57、 M (2,1) x2已知点 是抛物线 2py上的点,则以点M 为切点的抛物线的切线方程为
.
58、已知函数 f (x) | lg x |.若 f (a) f (b)且 a b,则 a b的取值范围是 .
59、一个袋子里装有大小相同的 3个红球和 2 个黄球,从中同时取出 2 个球,则其中含红球个数的数学期
望是 .
60、某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第 k棵树种植在点 Pk (xk,yk )
x k 1 k 2 k xk 1 1 5 T
5
T ,
x 1 y 1 k 2
5
≥ 处,其中 1 , 1 ,当 时,
y y T k 1 k 2 k
k 1 T
.
5
5
T (a)表示非负实数a的整数部分,例如T (2.6) 2 ,T (0.2) 0.按此方案第 2012 棵树种植点的坐
标应为______________.
第9页,共66页
高中数学填空题专练
4
61、计算: log 273 lg 25 2lg 2 e
ln 2
3
62、 f (x) xn
2 3n (n Z) 是偶函数,且 y f (x) 在 (0, )上是减函数,则 n
63、 2若关于 x的方程3tx (3 7t)x 4 0 的两实根 , ,满足 0 1 2 ,则实数 t的取值范
围是 。
x2 y2
64、 过双曲线 2 2 1(a 0,b 0) 的右焦点F和虚轴端点B作一条直线,若右顶点A到直线Fa b
b
B的距离等于 ,则双曲线的离心率 e
7
65、一个几何体的三视图如图所示,
则此几何体的体积是 .
3
4
正视图 侧视图
4
4
俯视图
第10页,共66页
高中数学填空题专练
66、若圆 x 2 y 2 2x 4y 1 0 关于直线 2ax-by+2=0(a,b∈R)对称,则 ab的取值范围是
___ .
67、一个几何体的三视图如图所示,则该几何体的体积为 .
68、已知 a (m,n),b ( p,q) ,定义 a b mn pq,下列等式中
① a a 0;②a b b a;③ (a b) a a a b a;
2 2
④ (a b) (a b) (m2 q2 )(n2 p2 )
一定成立的是 。(填上序号即可)
69、统计某校 1000 名学生的数学会考成绩,得到样本频率分布直方图如下图,规定不低于 60 分为及格,
不低于 80 分为优秀.则及格人数是 ;优秀率为 .
第11页,共66页
高中数学填空题专练
70、已知向量 a ( 3,1) ,b (0,1) c , (k , 3) ,若 a 2b 与 c 垂直,则 k .
71、设 a log 3 ,b ln 3, c 2 11 ,则这三个数由大到小的顺序为_________.(用“ ”连结各数)
2
72、已知 sin 5 ,则 cos 2 _____________.
5
2 2
73、已知椭圆C : x y1 2 2 1( a b 0 ,且 a,b为常数),椭圆C2 焦点在 y 轴上,椭圆C2 的长轴长与a b
椭圆C1 的短轴长相等,且椭圆C1 与椭圆C2 的离心率相等,则椭圆C2 的方程
为: .
74、设 z 1 i(i 2是虚数单位),则
z 2
z .
75、给出下列命题,其中正确的命题是 (写出所有正确命题的编号).
..
① 非零向量 a、 b满足 | a | | b | | a b | ,则 a与a b的夹角为30 ;
② 已知非零向量 a、 b,则“ a b 0 ”是“ a、 b的夹角为锐角”的充要条件;
③ 命题“在三棱锥O ABC中,已知OP xOA yOB 2OC,若点 P在△ABC所在的平面内,
则 x y 3”的否命题为真命题;
④ 若 (AB AC) (AB AC) 0,则△ABC为等腰三角形.
76、在等比数列 an 中, a1 1 ,公比 q 2 .若 an 64 ,则 n的值为
x y 4
77、当 x , y 满足不等式组 x 4 y时,点 (4,0)为目标函数 z ax 2y取得最大值时的最优解,则实
x 4
数 a的取值范围是
第12页,共66页
高中数学填空题专练
78、圆C的半径为 1,过点 P作圆C的两条切线,切点分别为 A , B .则 PA PB的最小值为
x2 y2
79、双曲线 1上一点 P 到右焦点的距离是实轴两端点到右焦点距离的等差中项,则 P 点到左焦
16 9
点的距离为 .
80、若不等式 (x y)(1 x y) 1对一切实数 x恒成立,则实数 y 的取值范围是 .
81、定义在 R 上的函数 y f (x) ,对任意不等的实数 x1, x2 都有[ f (x1) f (x2)](x1 x2) 0成立,又
函数 y f (x 1) 2的图象关于点 (1,0) 对称,若不等式 f (x 2x) f (2y y2 ) 0成立,则当1 x 4时,
y
的取值范围为 .
x
82、已知函数 y f (x) 是 R上的偶函数,对 x R都有 f (x 4) f (x) f (2)
成立.当 x , x 0,2 ,且 x x f (x时,都有 1) f (x2 )1 2 1 2 0 ,给出下列命题:x1 x2
(1) f (2) 0;
(2)直线 x 4是函数 y f (x) 图象的一条对称轴;
(3)函数 y f (x) 在 4,4 上有四个零点;
(4) f (2012) f (0)
其中正确命题的序号为__________(把所有正确命题的序号都填上).
第13页,共66页
高中数学填空题专练
2
83、幂函数 y (m2 m 1) xm 2m 3 ,当 x (0, ) 时为减函数,则实数 m 的值为
84、在 x a 10 7的展开式中, x 的系数是 15,则实数 a = ——
85、 2若 sin sin 1,则 cos 4 cos 2 = ——
86、 O x 2过原点 作圆 y 2 6x 8y 20 0的两条切线,设切点分别为 P、Q,则直线 PQ 的方程是——
87、对于 ABC,有如下命题:①若 sin 2A sin 2B ,则 ABC为等腰三角形;②若 sin A cosB则 ABC
2 2
为直角三角形;③若 sin A sin B cos 2 C 1则 ABC为钝角三角形.其中正确命题的序号是——
88、已知 x 0 , y 0 4 1 且 1,则 x y最小值是 .
x y
89、如图,已知图中的三个直角三角形是一个几何体的三视图,
那么这个几何体的体积等于_______.
第14页,共66页
高中数学填空题专练
90、若等差数列 {a n }的首项为 a1 ,公差为 d ,
S
前 n项的和为 Sn,则数列 { n }为等差数列,n
S d
且通项为 n a1 (n 1) 。类似地,请完成n 2
下列命题:若各项均为正数的等比数列 {bn }
的首项为 b1,公比为 q,前 n项的积为Tn,
则数列 。
13
7
3 15
91、对于大于 1 3 3 3 的自然数 m 的三次幂可以用技术进行以下方式的“分裂”:2 ,3 9 ,4 5
, ……
17
11
19
3
仿此,若m 的“分裂数”中有一个是 59,则m
92、若函数 f (x) a sin 2x b tan x 1,且 f (2) 5, 则 f ( 2) f ( ) __________
93、 f (x) | x | sin x 1已知函数 (x R)的最大值为M ,最小值为m,则M m ______
| x | 1
94、下列几个命题:
2
①方程 x (a 3)x a 0有一个正实根,一个负实根,则 a 0;
2 2
②函数 y x 1 1 x 是偶函数,但不是奇函数;
③函数 f (x) 的值域是[ 2,2],则函数 f (x 1)的值域为[ 3,1];
④设函数 y f (x) 定义域为 R,则函数 y f (1 x) 与 y f (x 1) 的图象关于 y 轴对称;
y | 3 x2⑤一条曲线 |和直线 y a (a R)的公共点个数是m,则m的值不可能是 1.
其中正确的有_________________
第15页,共66页
高中数学填空题专练
95、观察下列等式:
(1 x x2 )1 1 x x2 ,
(1 x x2 )2 1 2x 3x2 2x3 x4 ,
(1 x x2 )3 1 3x 6x2 7x3 6x4 3x5 x6 ,
(1 x x2 )4 1 4x 10x2 16x3 19x4 16x5 10x6 4x7 x8 ,
�
由以上等式推测:
n N , (1 x x2 )n a a x a x2 a x2n对于 若 0 1 2 2 n ,则 a2 .
96、如图,圆O是 ABC的外接圆,过点C的切线交 AB的延长线于点D,CD 2 7, AB BC 3,则 AC
的长为 .
C
D
O
B
A
97 、 在 (1 2x)3 (1 2 x )3 (1 33 x )3 的 展 开 式 中 , x 的 系 数
为 .(用数字作答)
98、若 A {x | y x 1},B {y | y x2 1},则A B= 。
99、已知 tan 2,
则1 1 sin 2 3cos2 .
2
第16页,共66页
高中数学填空题专练
100、一个容量为 20 的样本数据,分组情况及各组的频数如下:(10,20],2 ;(20,30],3 ;(30,40],4;(40,50],5 ;
(50,60],4; (60,70],2 .则样本数据在(-∞,30)上的概率为________
f (x) lg(2 x x
2 )
101、函数 的定义域是 。
x x
102、已知一个等比数列的前三项的积为 3,后三项的积为 9,且所有项的积为 243,则该数列的项数
为 。
103、已知定义在 R 上的偶函数 f(x)在[0,+∞)上是增函数,且 f(2)=1,若 f(x+a) ≤1 对 x∈[-1,1]恒成立,则
实数 a 的取值范围是 。
104、 2已知抛物线 y 2px 2的准线与双曲线 x y2 2 的左准线重合,则 p的值为
105、在等比数列{an}中,已知 a1 a
1
2 ,a3 a4 1,则 a7 a8 a9 a10 的值为2
x2 y2
106、已知椭圆的方程为 2 2 1(a b 0) ,过椭圆的右焦点且与 x 轴垂直的直线与椭圆交于 P、Qa b
两点,椭圆的右准线与 x 轴交于点 M,若 PQM 为正三角形,则椭圆的离心率等于
107、已知直线 x+ay=2a+2 与直线 ax+y=a+1 平行,则实数 a 的值为 。
x 1 1 , x [0, )
f (x)
2 2
108、已知函数 若存在 x1, x2 ,当0 x1 x2 2 时, f (x1) f (x2 ) ,则 x1 f (x2 )
2x 1, x 1 [ , 2)
2
的取值范围是
109、从 1,2,3,4,5 这 5 个数中一次随机取两个数,则这两个数的和为 5 的概率为 。
第17页,共66页
高中数学填空题专练
110、 *设数列{x n }满足 log 2 x n 1 1 log 2 x n (n N ) 且 x1 x 2 x10 10,
记{x n }的前 n 项和为Sn ,则S20
111、定义在实数集 R 上的奇函数 f x 满足 f (x) 2x 4(x 0) ,则不等式 f (x 2) 0 的解集是
_________
112、 Rt ABC , C 90 在 中,且 A. B. C所对边分别为 a,b,c,若 a b cx,则实数 x的取
值范围为 __________ .
2
113、 x 2x x关于 的不等式 4的解集为 .
114、 2圆 (x 1) (y 2)2 5 在 y 轴上截得的弦长为 .
115、在区间[-3,5]上随机取一个数 x,则 x [1,3]的概率为_________
116、定义在 R上的 f (x) 2,满足 f (m n ) f (m) 2[ f (n)]2 ,m,n R, 且 f (1) 0,则 f (2012) 的值
为
117、等比数列 an 中, a3 20, a6 160,则 an
118、将正偶数排列如下表其中第 i行第 j个数表示 a (i N * , j N *ij ) ,例
如a32 10,若 a ij 2012 ,
则 i j .
第18页,共66页
高中数学填空题专练
119、 0已知△ABC 中的一个内角为 120 ,并且三边长构成公差为 4 的等差数列,则△ABC 的面积
为 。
120 、 已 知 f (x) 是 定 义 在 R 上 的 不 恒 为 零 的 函 数 , 且 对 任 意 实 数 a 、 b 满 足
n n
f (a b) af (b) bf (a), f (2) 2,a f (2 ) (n N*),b f (2 ) n n n (n N*),有以下结论:n 2
① f (0) f (1) ② f (x) 为偶函数;③数列{an}为等比数列;④数列{bn}为等差数列。其中正确结
论的序号是 。
C
D
A
B
121、若集合 A { 1,0,1} , B {x | 0 x 2},则 A B ______ _____.
122、函数 f (x) 2 sin(2x ) 2 的最小正周期是 .
3
5i
123、复数 的实部是_________;
1 2i
第19页,共66页
高中数学填空题专练
4 3
124、已知正三棱锥的底面边长为 2,侧棱长为 3 ,则它的体积为 。
125、在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 .
甲 乙
8 2 9
9 1 3 4 5
2 5 4 8 2 6
7 8 5 5 3 5
6 6 7
2
126、函数 f x sin x cos x 的单调递增区间是 。
127、如果执行如图的流程图,那么输出的 S .
开始
S 0,i 1
i≤10 N
否
Y
S 输出 S
i i 2
结束
第 7 题
第20页,共66页
高中数学填空题专练
x 3,
128、由不等式组 y 0, 所确定的平面区域的面积等于__________;
y x 1,
129、已知向量 a,b满足 | a | 1,| b | 2,a (a b) ,则向量a,b夹角的大小为 .
130、如果底面直径和高相等的圆柱的侧面积是π,则这个圆柱的体积是 .
131、 p x [ 0,1] k 4 x k 2 x 1已知命题 :对一切 , 6(k 5) 0 ,若命题 p是假命题,
则实数 k的取值范围是 .
132、已知集合 A={1,2},B={-1,0,1},则 A∪B= 。
133、过点(1,0)且与直线 x 2y 2 0平行的直线方程是 .
A x Z x2 5x 0 B x x 4 0 (C A) B
134、已知全集U R,集合 , 则 U 中最
大的元素是 ▲ .
135、 如图,⊙O中,直径 AB 和弦 DE 互相垂直,C 是 DE 延长线上一点,连结 BC 与圆 0 交于 F,
若∠CFE= ( (0, ) ),则∠DEB___________
2
第21页,共66页
高中数学填空题专练
x 1136、 n已知( ) 展开式的第 4项为常数项,则展开式中各项系数的和为________
2 3 x
137、 2已知数列{an}的前 n 项和 Sn=n -7n,且满足 16
138、设点 A,B 分别在曲线 C1 : ( 为参数)和曲线 C2 : 1上,则 |AB|的最小值
y sin
为 。
139、设向量 a (cos , 1),b (1, 3cos ) ,且 a //b,则 cos2 = .
140、关于 x的不等式 | x 2 | | x a | 2a在 R上恒成立,则实数 a的最大值是 .
141、将函数 y sin x( 0)的图象向左平移 个
6
单位后的图象如图所示,则平移后的图象所
对应的函数的解析式是 。
y
1
7
12
0 x
-1
第22页,共66页
高中数学填空题专练
142、从一个棱长为 1的正方体中切去一部分,得到一个几何体,其三视图如右图,则该几何体的体积为
______________
143、已知m (cos x, sin x)( 0),n (1, 3),若函数 f (x) m n的最小正周期是 2,
则 f (1) ▲ .
144、已知函数 f (x)
x (0, )
1 2x tan x, 2 ,则 f (x) 的单调减区间是 ▲ .
145、P 为抛物线 y
2 4x上任意一点,P 在 y 轴上的射影为 Q,点 M(4,5),则 PQ 与 PM 长度之和的
最小值为: ▲ .
x y 2 0
y 2 0
x y 2 0 2 2146、过平面区域 内一点 P作圆O : x y 1的两条切线,切点分别为 A,B,
记 APB ,则当 最小时cos ▲ .
第23页,共66页
高中数学填空题专练
147、如图所示的数阵叫“莱布尼兹调和三角形”,他们是由整数的倒数组成的,第 n行有 n个
1 (n 2)
数且两端的数均为 n ,每个数是它下一行左右相邻两数的和,
1 1 1 1 1 1 1 1 1
, ,
如:1 2 2 2 3 6 3 4 12 …,则第 n(n 3) 行第 3 个数字是 ▲ .
k k 1MB MD
148、已知正方形 ABCD的坐标分别是 ( 1,0) , (0,1) , (1,0), (0, 1) ,动点 M 满足: 2 则
MA MC ▲ .
149、若过定点M ( 1, 0)且斜率为 k 的直线与圆 (x 2)2 y 2 9 在第一象限内的部分有
交点,则 k 的取值范围是 。
150、在平面几何里,有:“若 ABC的三边长分别为 a,b,c, 内切圆半径为 r ,则三角形面积为
S 1 ABC (a b c)r ”,拓展到空间,类比上述结论,“若四面体 A BCD的四个面的面积分别为2
S1,S2 ,S3 ,S4 ,内切球的半径为 r,则四面体的体积为 ”
151、 2设斜率为 2 的直线 l过抛物线 y ax(a 0) 的焦点 F,且和 y 轴交于点 A,若 OAF (O 为坐标原
点)的面积为 4,则抛物线方程为 。
152、已知如下算法语句
输入 t;
If t<5 Then
y=t2+1;
Else
if t<8 Then
第24页,共66页
高中数学填空题专练
y=2t-1;
Else
y= 8t 1 ;
End If
End if
输出 y
若输入 t=8,则下列程序执行后输出的结果是 .
2x 1(x 1)
153、已知 f (x) 则f [ f ( )]
sin x 2(x 1)
y 1,
154、若实数 x,y满足 y 2x 1,如果目标函数 z x y的最小值 1,则实数 m= 。
x y m.
155、已知关于 x的不等式: 2x m 1的整数解有且仅有一个值为 2.则整数m的值为____________.
3 2
156、不等式 的解集为
x x 1
1
157、若不等式 2a 1 x x 对一切非零实数 x恒成立,则实数 a的取值范围
158、已知 ABC的内角 A,B,C 所对的边分别为 a,b,c,且 a 2,b 3, cosB 4 .
5
则 sin A的值为 .
ABC cos( A) : sin B : cos(3 159、在 中,若 C) 3 : 2 : 4 ,则 cosC的值为
2 2
160、从甲、乙等 5 人中选出 3 人排成一排,则甲不在排头的排法种数是 (用数字作答)
第25页,共66页
高中数学填空题专练
x y 2
161、已知实数,x,y 满足约束条件 y x 2 ,则 z=2x+y的最小值是____
y 1
1 4
162、已知 a,b,c>0 且 a+2b+c=1,则 的最小值为
a b b c
(二)选考题(请考生在第 15、16 两题中任选一题作答,请先在答题卡指定位置将你所选的题目序号后
的方框用 2B 铅笔涂黑. 如果全选,则按第 15 题作答结果计分.)
10 10 1
163、已知 xi>0(i=1,2,3,…10.),且 xi=1. 则 T= 的最小值为
i 1 i 1 x i
� 164、 如图,PA是圆O的切线,A是切点,直线 PO交圆O于 B、C 两点,D是OC的中点,连结 AD
并延长交圆O于点 E,若 PA 2 3 ,∠ APB 30 ,则 AE ________.
�A
�P �D
�B �O �C
�E
165、某种产品的广告费支出 x与销售额 y之间有如下对应数据(单位:百万元).
x 2 4 5 6 8
y 30 40 60 t 70
根据上表提供的数据,求出 y关于 x的线性回归方程为=6.5x+17.5,则表中 t的值为 .
166、设等差数列{an}的前 n项和为 Sn,若 a2 a5 a8 15,则 S9 = .
167、二项式 ( x 2 10
x2
) 展开式中的常数项是 .
第26页,共66页
高中数学填空题专练
f (x) D , f (x) D , a,b168、 D f (x) a,b, 函数 的定义域为 若满足① 在 内是单调函数 ②存在 使 在 上的
b, a
值域为 ,那么 y f (x) 叫做对称函数 ,现有 f(x) 2 x k是对称函数 , 那么 k 的取值范围是
▲ .
169、在边长为 2 的正三角形 ABC 中,以 A 为圆心, 3 为半径画一弧,分别交 AB,AC 于 D,E.若在△ABC
这一平面区域内任丢一粒豆子,则豆子落在扇形 ADE 内的概率是________.
sin( ) sin( )
170、已知 tan 2 ,则 2 的值为 .
cos(3 ) cos( )
2
171、如右图所示,一个三棱锥的三视图是三个直角三角形 (单位:cm),则该三棱锥的外接球的表面积为
__________cm2.
172、设 f (x) 是定义在R上的偶函数,对任意 x R,都有 f (2 x) f (x 2)成立,且当 x [ 2,0]时,
x
f (x) 1 1.若关于 x的方程 f (x) log a(x 2) 0 (a 1)在区间 (0,6]内恰有两个不同实根,则实
2
数 a的取值范围是 .
173、 (1 x)(1 x)5展开式中x 4 的系数是 (用数字作答).
第27页,共66页
高中数学填空题专练
174、设互不相同的直线 l,m,n 和平面α、 、 ,给出下列三个命题:
①若 l与 m 为异面直线, l ,m ,则α∥
②若α∥ , l ,m ,,则 l∥m;
③若 l, m, n, l∥ ,则 m∥n.
其中真命题的个数为______
175、定义:对于映射 f : A B,如果 A 中的不同元素有不同的象,且 B 中的每一个元素都有原象,则
称 f : A B为一一映射.如果存在对应关系 ,使 A到 B成为一一映射,则称 A和 B具有相同的势.给
出下列命题:
①A={奇数},B={偶数},则 A和 B 具有相同的势;
②A是直角坐标系平面内所有点形成的集合,B是复数集,则 A和 B 不具有相同的势;
③若 A= a,b ,其中 a,b是不共线向量,B= c | c与a,b共面的任意向量 ,则 A和 B不可能具有相
同的势;
④若区间 A= -1,1 ,B= , ,则 A和 B具有相同的势.
其中真命题为
3
176、设α为△ABC 的内角,且 tanα=- ,则 sin2α的值为____
4
lg(x 1) x 1
1
177、若函数 y=f(x)(x∈R)满足 f(x-2)=f(x),且 x [ 1,1]时,f(x)=1-|x|,函数 g(x) x 0 ,则方
x
0 0 x 1
程 f(x)-g(x)=0 在区间[-5,6]内的解的个数为_______.
178、集合 A x | x2 9 0 ,集合 B x | x 1x 2 0 ,则 A B =_ _.
179、下列图形中,若黑色三角形的个数依次构成一个数列的前 4 项,则这个数列的一个通项公式为 an
第28页,共66页
高中数学填空题专练
n N * .
a x
180、已知函数 f(x)的定义域为 D,[a,b]为包含于 D的任意一个区间,若对任意的 x0∈(a,b),m 0 ,
2
x b
n 0 ,都有 | f (m) f (n) | | f (a) f (b) | ,则称 f(x)为 函数.
2
那么下列函数中, 函数有 .(请填上你认为正确命题的所有序号)
① f (x) 2 sin(x ) ; ② f (x) 2 x 1 ;
4
③ f (x) 1 x3 x2 3x 2 ; ④ f (x) ln (x 1) ,
3
181、若 f x 是 R上的奇函数,则函数 y f x+1 -2的图象必过定点 .
2 2
182、已知 F1,F
x y
2 分别是双曲线 2 2 1 a 0,b 0 的左、右焦点,以 F1F2 为直径的圆a b
与双曲线在第一象限的交点为P,则当 PF1F2 的面积等于 a2 时,双曲线的离心率为 .
x t 4cos
183、在曲线 为参数 上,仅存在四个点到点 1,0 距离与到直线 x 1的距离相等,
y 4sin
则 t的取值范围是
184、定义: S为 R的真子集, x, y S,若 x y S , x y S,则称 S对加减法封闭。
有以下四个命题,请判断真假:
①自然数集对加减法封闭;②有理数集对加减法封闭;
③若有理数集对加减法封闭,则无理数集也对加减法封闭;
④若 S1,S2为 R的两个真子集,且对加减法封闭,则必存在 c R,使得 c S1 S2 ;
四个命题中为“真”的是 ;(填写序号)
第29页,共66页
高中数学填空题专练
185、已知 AD是 ABC的中线,若 A 120 , AB AC 2,
则 AD 的最小值是__________ .
1
186、 2 8(1+2x )(x- ) 的展开式中常数项是________(用数字作答);
x
x 0,
187、已知 x、y 满足约束条件 y 0, 则z x 2y的最小值
x y 2,
为 .
1
188、 ! *已知 an=错误 ,数列{ }的前 n 项和为 Sn,bn=n-33,n∈N ,则 bnSn的最小值为__________.
an
189、 3 2 3对任意的实数 x,有 x a0 a1 (x 2) a2 (x 2) a3 (x 2) ,则 a2的值是 。
190、若点 P(cos ,sin ) 在直线 y 2x上,则 sin 2 2cos 2 = .
191、若某程序框图如图所示,则该程序运行后输出的 s .
第30页,共66页
高中数学填空题专练
192、设有算法如图:如果输入 A=144, B=39,则输出的结果是 .
开始
输入非零正整数 A,B
是
B=0? 输出 A 结束
否
C=A 除以 B 的余数
A=B
B=C
1 a 1
193、若二项式 (a x )6 的展开式中的常数项为 160 ,则 ( x )dx = .x 1 x
194、一个总体分为 A,B两层,其个体数之比为 4 :1,用分层抽样法从总体中抽取一个容量为 10 的样本,
1
已知 B层中甲、乙都被抽到的概率为 ,则总体中的个体数是 .
28
第31页,共66页
高中数学填空题专练
195、选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
A.(选修 4—4 坐标系与参数方程)已知点 A 是曲线 2sin 上任意一点,则点 A 到直线
sin( ) 4的距离的最小值是 .
3
B.(选修 4—5 不等式选讲)不等式 | x log 2 x | x | log 2 x | 的解集是 .
C.(选修 4—1 几何证明选讲)如右图所示, AC和
AB分别是圆O的切线,且OC 3, AB 4 ,延长
AO到D点,则 ABD的面积是 .
196、已知集合 A {x x 2},B {x ln(x 1) 0},则 A B = .
197、某算法流程图如图所示,则输出的结果是 .
198、已知一个四棱锥的三视图如图所示,则该四棱锥的体积是 ______ .
第32页,共66页
高中数学填空题专练
1 1
2 2
主视图 左视图
2
俯视图
x y 2
199、已知 O 是坐标原点,点 A(-1,-2),若点 M(x,y)平面区域 x 1 上的一个动点,使
y 2
OA (OA MA) 1 0恒成立,则实数 m 的取值范围为_____________.
m
200、如图是 2012 年某高校自主招生面试环节中,7 位评委对某考生打出的分 数茎叶统计图.去掉一个最
高分和一个最低分后,所剩数据的平均数为____,方差为____.
1
201、在等差数列{an}中,若 a9=6 则 a7 a3 = .3
202、如图,曲线 OB 2的方程为 y x(0≤x≤1),为估计阴影部
分的面积,采用随机模拟方式产生菇∈(0,1),y∈(0,1)的
200 个点(x,y),经统计,落在阴影部分的点共 134 个,则估
计阴影部分的面积是 .
第33页,共66页
高中数学填空题专练
203、一个几何体的三视图如图所示,其中正视图是腰长为 2 的等
腰三角形,俯视图是半径为 1 的半圆,则该几何体的表面积
是 .
204、若二项式 (3x2 1 )n 的展开式中各项系数的和是 64,则展开式中的常数项为 .
x
1 2
205、 2已知随机变量 服从正态分布 N (1, ) ,P( m) ,P( m 1) ,则实数m ___________.
3 3
x 3y 5 0
206、已知变量 x, y 满足 2x y 0 ,则 z log2 x log2 y 1 的最大值为_____.
x 0, y 0
第34页,共66页
高中数学填空题专练
y ln( x
2 2x 3)
207、函数 的定义域为 。
x 1
x 3y 5 0
208、 已知变量 x, y满足 2x y 0 ,则 z log2(2x y) 的最大值为__________.
x 0, y 0
209、 3 2对于三次函数 f (x) ax bx cx d( a 0),定义:设 f (x)是函数 y=f(x)的导数 y= f (x)
的导数,若方程 f (x)=0 有实数解 x0,则称点(x0,f(x0))为函数 y=f(x)的“拐点”.有同学发现“任何
一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”
3 1
请你将这一发现为条件,函数 f (x) x3 x2 3x ,则它的对称中心为 ;
2 4
1
计算 f ( ) 2 f ( ) f ( 3 ) 2012 f ( ) = .
2013 2013 2013 2013
(二)选做题(14-15题,考生只能从中选做一题. 两题都答的按第 14题正误给分.)
5
210、 a x 1 x 的展开式中 x2 项的系数是 15,则展开式的所有项系数的和是_______
211、如图,⊙O1与⊙O2相交于 A、B 两点,过点 A 作⊙O1的切线交⊙O2于点 C,过点 B 作两圆的割线,分
别交⊙O1、⊙O2于点 D、E,DE 与 AC 相交于点 P.若 AD 是⊙O2的切线,且 PA=6,PC =2,BD =9,则 AD 的
长为________。
212、某校高三年级共 1500 人,其中高三(2)班学生人数为 60 人.学校为了检查同学们的健康状况,随
机抽取了高三年级的 100 名同学作为样本,测量他们的体重(单位:公斤),体重的分组区间为[40,45),
[45,50),[50,55),(55,60),[60,65],由此得到样本的频率分布直方图,如图 3.根据频率分布直
方图,估计该校体重低于 50 公斤的人数为_________;若用分层抽样方法,则高三(2)班应抽取
_________人.
第35页,共66页
高中数学填空题专练
213、(坐标系与参数方程选做题)在极坐标系中,直线 l经过圆 2cos
的圆心且与直线 cos 3平行,则直线 l与极轴的交点的极坐标
为_________.
n,n为奇数
214、 *已知数列 an 的递推公式 an a ,n为偶数(n N ) ,则 a24 a25 ;数列 an
n 2
中第 8 个 5 是该数列的第 项.
215、 f (x) ax3 bx 2对于三次函数 cx d( a 0),定义:设 f (x)是函数 y=f(x)的导数 y= f (x)
的导数,若方程 f (x)=0 有实数解 x0,则称点(x0,f(x0))为函数 y=f(x)的“拐点”.有同学发现“任何
一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”
3 1
请你将这一发现为条件,函数 f (x) x3 x2 3x ,则它的对称中心为 ;
2 4
计算 f ( 1 ) f ( 2 ) f ( 3 ) 2012 f ( ) = .
2013 2013 2013 2013
216、连掷两次骰子得到的点数分别为m,n.记向量 a (m,n) 与向量b (1, 1)的夹角为 ,则 (0, ]
2
的概率是_______________.
217、在某次测量中,测量结果 服从正态分布 N(1, 2 ) ,
若 在(0,1)内取值的概率 0.35, 则 在(0,2)内取值的概率为________.
218、已知有公共焦点的椭圆与双曲线中心为原点,焦点在 x轴上,左右焦点分别为 F1,F2 ,且它们在第一
象限的交点为P, PF1F2 是以 PF1为底边的等腰三角形.若 PF1 10 ,双曲线的离心率的取值范围为 (1, 2).则
该椭圆的离心率的取值范围是 .
第36页,共66页
高中数学填空题专练
2
219、记 (x )n 的展开式中第 k 项的系数为 ak ,若a3 5a3 ,则n = _________x
220、 设双曲线的一个焦点为 F,虚轴的一个端点为 B,如果直线 FB 与该双曲线的一条渐近线垂直,那
么双曲线的离心率是_________
a i
221、已知 a R,且 为纯虚数,则 a 。
1 i
222、平面上有一组平行线,且相邻平行线间的距离为 3cm,把一枚半径为 1cm 的硬币任意平掷在这个平
面上,则硬币不与任何一条平行线相碰的概率为 。
223、若直线 y x b与圆 x2 y2 2相切,则 b的值为 。
a i
224、设 i 为虚数单位,若 为实数,则实数 a 的值为 .
1 i
225、已知等差数列{an}的前 n项和为 Sn,若 a3 a6 10,则 S8 的值为________.
226、(极坐标与参数方程选做题)极坐标系下,圆 2cos( )上的点与直线 sin( ) 2 的
2 4
最大距离是 .
227、如图是长方体截去一个角后的多面体的三
视图,则这个多面体的体积为 .
6
3
正视图 侧视图
4
第37页,共66页
俯视图
高中数学填空题专练
228、已知集合M {1, 2,3, ,n}(n N ),若集合 A {a1,a2 ,a3 , ,am} M (m N
) ,且对任意的 b M ,存
在 ai ,a j A(1 i j m),使得 b = 1ai + 2a j(其中 1, 2 { 1,0,1}),则称集合 A为集合M 的一个m -
生成元.若集合 A为集合M = {1, 2,3, ,8}的一个m - 生成元,则m的最小可能值为 .
229、为调查学生的身高与饮食习惯的关系,某中学将
高三同学的身高(单位:厘米)数据绘制成频率分布
直方图(如图).现采用分层抽样的方法从中选取 40
名进行调查,则身高在 [160,170]内的学生中应选取的
人数为 .
2 2
230、若抛物线 y2 8x x y的焦点到双曲线 2 2 1(a 0,b 0) 一条渐近线的距离为 2 ,则双曲a b
线的离心率为 .
x
shx e e
x
chx e
x e x
231、定义“ , x R”为双曲正弦函数,“ , x R”为双曲
2 2
余弦函数,它们与正、余弦函数有某些类似的性质,如:sh(x y) shx chy chx shy 、(chx)2 (shx)2 1
等.请你再写出一个类似的性质: ch(x y) .
第38页,共66页
高中数学填空题专练
2i
232、复数 Z 的虚部是
1 i
233、某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这
些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规
律相同),设第n个图形包含 f (n) 个小正方形,则 f (6) 。
2
234、 在平面直角坐标系 xOy中,椭圆 C的中心为原点,焦点 F1, F2 在 x轴上,离心率为 .过 F1的
2
直线 l交 C于 A,B两点,且△ABF2 的周长为 16,那么 C的方程为________
235、数列 an 的前 n项和为 Sn,若数列 an 的各项按如下规律排列:
1 , 1 , 2 , 1 , 2 , 3 , 1 , 2 , 3 , 4 ,..., 1 , 2 ,... n 1,...有如下运算和结论:
2 3 3 4 4 4 5 5 5 5 n n n
a 3① 23 ;8
②数列 a1,a2 a3 ,a4 a5 a6 ,a7 a8 a9 a10 ,... 是等比数列;
2
③数列 a1,a2 a3 ,a
n n
4 a5 a6 ,a7 a8 a9 a10 ,... 的前 n项和为Tn ;4
④若存在正整数 k,使 Sk 10, S
5
k 1 10 ,则 ak .7
以上所.有.正确结论的序号是 .
236、在如图所示的茎叶图中,乙组数据的中位数
是 ;若从甲、乙两组数据中分别去掉一个最大
数和一个最小数后,两组数据的平均数中较大的
第39页,共66页
高中数学填空题专练
一组是 组.
甲 乙
0 7 9
5 4 5 5 1 8 4 4 6 4 7
m 9 3
237、某工厂经过技术改造后,生产某种产品的产量 x (吨)与相应的生产能耗 y (吨标准煤) 有如下几
组样本数据:
x 3 4 5 6
y 2.5 3 4 4.5
根据相关性检验,这种样本数据具有线性相关关系,通过线性回归分析,求得回归直线的斜率为 0.7,
那么这组样本数据的回归直线方程是________________.
x2 16y2
238、双曲线 12 ( p 0) 的左焦点在抛物线 y2 2px 的准线上,则该双曲线的离心率3 p
为 .
239、某几何体的三视图,其中正视图是腰长为 2的等腰三角形,侧视图是半径为 1 的半圆,则该几何体的
表面积是 .
240、 某班级有 50 名学生,现要采取系统抽样的方法在这 50 名学生中抽出 10 名学生,将这 50 名学生
随机编号 1—50 号,并分组,第一组 1—5 号,第二组 6—10 号,……,第十组 46—50 号,若在第三组中
抽得号码为 12 的学生,则在第八组中抽得号码为___ 的学生.
第40页,共66页
高中数学填空题专练
�
241、 f (x) = 1+ x
2 + 1+ (1- x)2 (0#x 1)
某同学为研究函数 的性质,构造了如图所示的两个边
长为 1 的正方形 ABCD和 BEFC,点 P是边 BC上的一个动点,设CP = x,则 AP + PF = f (x) .
请你参考这些信息,推知函数 f (x) 的图象的对称轴是 ;函数 g(x) = 4 f (x)- 9的零点的个数
是
D C F
P
A B E
242、已知向量 a、b 的夹角为60 ,|a|=2, |b|=3,则|2a-b |= .
243、如图所示:有三根针和套在一根针上的 n 个金属片,按下列规则,把金属片从一根针上全部移到另
一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的
金属片上面.将 n 个金属片从 1 号针移到 3 号针最少需要移
动的次数记为 f (n);
则:(Ⅰ) f (3) (Ⅱ) f (n)
第 17 题图
244、 函数
(1)若 a=0,则方程 f(x)=0 的解为_______.
第41页,共66页
高中数学填空题专练
(2)若函数 f(x)有两个零点,则 a 的取值范围是_______.
245、命题“ x0 (0, ), tan x sin x ”的否定是 .2 0 0
246、已知△ ABC中, AD BC于D, AD BD 2 ,CD 1,则 AB AC ___.
247、设抛物线的顶点在原点,其焦点 F 在 y轴上,抛物线上的点 P(k, 2) 与点 F 的距离为 4,则抛物线方
程为 .
248、等比数列 an 的前 n项和为 Sn,已知 S1 ,2S2 ,3S3 成等差数列,则 an 的公比为 .
249、已知某算法的流程图如图所示,若将输出的 (x, y) 值依次记为
(x1 , y1), (x2 , y2 ) , , (xn , yn ), .
(1)若程序运行中输出的一个数组是 (t, 8) ,则 t ;
( 2)程序结束时,共输出 (x, y) 的组数为 .
第42页,共66页
高中数学填空题专练
x, x 0
250、. 已知 f x x, x 0 ,则不等式 x x f x 2的解集是_________.
2x y 6 0
251、 设不等式组 x y 3 0 所表示的平面区域为M ,若函数 y k x 1 1的图像经过区域M ,
y 2
则实数 k的取值范围是_________.
252、 2若集合 M= 1,m ,集合 N= 2,4 ,M N 1,2,4 ,则实数m的值的个数是_________
253、已知数列 an 的前 n项和 S n 2n 7n,且满足16 ak ak 1 22 ,则正整数 k _____
3
x t 2
254、(极坐标与参数方程)已知曲线 C的极坐标方程是 2sin ,直线 l 的参数方程是 5 (t
y 4 t 5
为参数).设直线 l与 x轴的交点是 M,N 是曲线 C 上一动点,则 MN 的最大值为____________
1
255、 f (x) 1 ( ) x函数 的定义域是 .
2
第43页,共66页
高中数学填空题专练
256、 a= (x 1,2), b = (4, y) , a b 9 x 3 y已知向量 若 ,则 的最小值为 .
257、在等比数列{an}中,若 a3 ,a
2
9 是方程3x 11x 9 0的两根,则 a6 的值是 .
(二)选择题(14-15 题,考生只能从中选做一题。两题都答的按第 14 题正误给分。)
258、曲线 y x3与直线 x 1及 x轴所围成的图形的面积为 .
259、从圆 O外一点 A 引圆的切线 AD和割线 ABC,已知 AD=4,AC=8,圆 O半径为 5,则圆心 O到直
线 AC的距离为 。
x t cos x 4 2cos
260、直线 (t为参数),与圆 ( 为参数)相切,则此直线的倾斜角
y t sin y 2sin
= .
261、 如图,在△ ABC中,D是边 AC上的点,且 AB AD, 2AB 3BD,BC 2BD,
则 sinC的值为 .
262、一个六棱柱的底面是正六边形,其侧棱垂直于底面.已知该六棱柱的顶点都在同一个球面上,且这
4
个球的体积为 ,已知该六棱柱的高为 3 ,则这个六棱柱的体积为 。
3
第44页,共66页
高中数学填空题专练
263、已知△ ABC为锐角三角形,若 A 2B a,则 的取值范围是 。
b
264、如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数
之和是 _________ .
甲 乙
53 41 5
368 2 6 3 7 8
2
479 3 57
1 4
x 2y 1 0,
265、已知实数 x,y 满足 且 z 3x y的最大值是 。
| x | y 1 0
1
266、若不等式 | x | | a 2 | 1对一切非零实数 x均成立,则实数 a的取值范围是 __________ .
x
267、点 M,N分别是曲线 sin 2和 2cos 上的动点,则|MN|的最小值是 .
以下是答案
一、填空题
1、 ①④
2、196
3、内角平分线
4、
5、
第45页,共66页
高中数学填空题专练
6、 2
7、【答案】 3 1
【解析】解:设正六边形的边长为 2c,则焦距为 2c,连接 EA,ED,则在三角形 EAD 中,
|EA|+|ED|=2a,DE AE DE 2 AE 2 AD2 ,DE 1 AD ,解得
2
AE 3c, 3c c 2a, e 3 1,故答案为 3 1
8、 4
9、3
10、 k ,k (k Z ) 4 4
3
11、
2
19
12、
6
13、-20【解析】
14、-3【解析】 f (x)是奇函数, f (1) f ( 1) [2 1} 3
15、D
16、
17、 700
1
18、
7
19、 4
20、2
第46页,共66页
高中数学填空题专练
21、72
22、11
23、2
24、
25、
26、
27、
28、
29、
30、
31、
32、答案: k 8
第47页,共66页
高中数学填空题专练
解析: n 1时, a1 S1 1 9 8,当n 2时,an Sn Sn 1 n
2 9n (n 1)2 9(n 1)
2n 10 , n 1时适合此式, an 2n 10 ,5 2k 10 8,7.5 k 9,又k N k 8
33、
34、
35、C 0 1 2 3n Cn Cn Cn
1
36、 ( ,1]
2
37、
38、 31
39、
40、 答案:原点
1
解析:由 lga+lgb=0 ab=1 b g x x= ,所以 ( )=- a ,故 f(x)与 g(x)关于原点对称.
a
41、
42、 【答案】10 年
1000 a b a 500
【解析】 y 500x2 bx.
3000 4a 2b b 500
M 50000 6000 500x 50000 500 500x 6500 16500.
年均消耗费用 x x
当x 10时,M最小.
第48页,共66页
高中数学填空题专练
所以使用 10 年最佳.
43、
三,解答题:
44、 1 i
45、 ①②
46、 684
3
47、
4
48、 3
49、 -1
50、 3a2答案: 10ab 3b2 4 0
解析:该题综合考查直线与圆锥曲线的位置关系,向量线性表示及坐标运算.可求出 e1 (1,1),e2 (1, 1) ,
a b x 2
设 P(x , y ) 0 (a b)0 0 ,则 , (a b)
2 1,
a b y0 4
3a2 10ab 3b2 4 0
9
51、 答案:
5
解析: sin y x , cos , 直线l的方程为3y-4x=2
即4x 3y 2 0,点 ( 2, )为 (1, 1),d (4 3 2) 9
4 42 ( 3)2 5
52、 答案:300
解析:连结OC,则OC OD, AD CD, OC / /AD, DAC OCA
BC 3 1 AB, CAB 300 ,又 OC OA, OCA 300 , DAC 300
2
第49页,共66页
高中数学填空题专练
53、答案:[2, ) {0}
解析:该题考查函数性质以及解二次不等式和解不等式组,容易产生漏解.
54、答案:i
解析:该题考查复数的运算及其概念,属于简单题.
55、答案:必要不充分条件.
解析:考查集合及其运算以及简易逻辑,是简单题.
56、答案:3
解析:该题考查抽样方法、总体分布的估计、总体特征数的估计.由
(0.005+0.010+0.020+0.035+a) 10=1得 a 0.030 ,因此, [120,130﹚,[130,140﹚,[140,150]三
组学生人数分别为:0.3 100 30,0.20 100 20,0.10 100 10,所以, 从身高在[140,150]内的学生
10
中选取的人数应为 18 3
30 20 10
57、 x y 1 0
58、 答案: (2, )
解析:该题考查对数函数及其性质,还有基本不等式;因为函数 f (x) | lg x |.若 f (a) f (b)且 a b ,所
以, lgb lg a , ab 1, a b a
1
2
a
6
59、
5
60、
15
61、 【答案】
4
第50页,共66页
高中数学填空题专练
【解析】
4
log 273 lg 25 2lg 2 e
ln 2
3
1
log 43 3 2(lg5 lg 2) 2
1
2 2
4
15
.
4
62、 【答案】 1或 2
【解析】因为 y f (x) 在 (0, )上是减函数,所以
n2 3n 0, 0 n 3, n Z n 1或2. 符合偶函数.
7
63、 【答案】 ( ,5)
4
2
【解析】设函数 f (x) 3tx (3 7t)x 4, 则满足0 1 2的条件为:
f (1) 0 7 4t 0
f (2) 0 即 10 2t
7
0 t 5. [
4
f (0) 0 4 0
64、 【答案】2
x y
【 解 析 】 因 为 直 线 FB 方 程 为 1,bx cy bc 0, 右 顶 点 A(a,0) ,
c b
b ab bc 4
8a2 14ac 5c2 0, 5e2 14e 8 0,e 2或 (舍去).
7 b2 c2 5
65、80
1
66、 答案: ( , ]
4
2 2
解析: 该题考查直线与圆的位置关系和二次函数的性质;因为圆 x y 2x 4y 1 0关于直线 2ax-
1
by+2=0(a,b∈R)对称,所以,点 ( 1,2) 在直线 2ax-by+2=0 上,所以,a+b=1,ab a(1 a)
4
3
67、π+
3
第51页,共66页
高中数学填空题专练
68、①、④
69、
800, 20%
70、 3
71、b c a;
3
72、 ;
5
y 2 x 2
73、
b 2
b 4
1
a 2
74、1
75、 ① ③ ④
三解答题:
76、7;
77、 a 2 ;
78、 2 2 3
79、13
80、 ( 1 , 3)
2 2
1
81、[ ,1]
2
82、(1)(2)(4);
83、答案:2
第52页,共66页
高中数学填空题专练
m2 m 1 1
解析:只要根据幂函数的定义及性质即可得出 m 2 ,学生在幂函数概念方面容易出2
m m 3 0
错,;考查幂函数概念与性质、函数性质,是中档题。
1
84、 -
2
85、1
86、 3x 4y 20 0
87、③
88、9
89、10
n 1
90、数列{n Tn} 为等比数列,且通项为 n Tn b1q 2 ;
91、M=8
92、 2 ;
93、 答案:2
解析: 该题 f (x) g(x) m且 g(x) 是奇函数的形式的函数,但是不注意又不易看出,增加做题的难度,既
考查函数性质又转化化归能力,是中档题。
f (x) | x | sin x 1 sin x
sin x
因为 1而 是奇函数,所以, M m 2
| x | 1 | x | 1 | x | 1
94、
第53页,共66页
高中数学填空题专练
n(n 1)
95、
2
3 7
96、
2
97、 21
98、答案:[1, )
解析:由 A {x | y x 1},B {y | y x2 1}简单考查函数的定义域与值域,由 A B考查集合
的交运算, A [ 1, ),B [1, ), A B [1, ) 。属于简单题。
99、
1
100、
4
101、(-1,0)
102、10;
103、[ 1,1]
第54页,共66页
高中数学填空题专练
104、2 ;
105、12;
3
106、 ;
3
107、1;
108、 [2 2 , 1) .
4 2
1
109、 5
110、 10250
111、 [ 4, 2] [0, )
112、 1,, 2
三解答题
113、 2,1
114、4
1
115、 .
4
116、1006;
117、5 2n 1
118、62
119、答案: 15 3
解析:由题意可以设三边长分别为:a-4,a,a+4,则由余弦定理得:
(a 4)2 a2 (a 4)2 2a(a 4)cos120 , a 10, 由正弦定理面积公式得:
第55页,共66页
高中数学填空题专练
S 1 a(a 4)sin120 15 3 。这是今年的一道高考题,综合考查等差数列概念,正余弦定理,是中档
2
题。
120、答案: ①③④
解 析 : 因 为 a,b R, f (a b) af (b) bf (a), 取a 1,b 1,得f (1) 0, 取 a=2,b=2, 得
f (4) 4 f (2) 8, 取 a 0,b 2 得 f (0) 2 f (0), f (0) 0, 取 a=-2,b=-2, 得
f (4) 4 f ( 2), f ( 2) 2,取 a 2,b 2n 1, f (2n ) 2 f (2n 1) 2n 1得 f (2)
f (2n ) f (2n 1 n
2 f (2n 1) 2n , ) f (2 ) 1, (1) 由 a (n N*) 得 f (2n ) na 代入(1)得
2n 2n 1 n n n
nan (n 1)an 1 na
n n 1 1, a1 f (2) 2,
n
n n, a
n
n 2 。该题通过函数方程考查函数性质与递推数2 2 2
列求数列通项公式,既考查函数方程问题一般的研究方法:赋值,又考查转化化归,对能力要求较高,是
难题。
121、{0,1}
122、
123、2
2 3
124、 3 ;
125、 45 46
k 126、 ,k
(k Z )
4 4
127、 25
128、 2
第56页,共66页
高中数学填空题专练
129、 120
130、
4
131、 [5, 6]
1,0,1,2
132、 ;
133、 x 2y 1 0
134、3
135、a
1
136、
32
137、8
138、1
1
139、
3
2
140、
3
141、 y sin 2x
3
5
142、
6
第57页,共66页
高中数学填空题专练
143、-1
( , )
144、 4 2
145、 34 1解析:焦点 F (1,0) PM PQ =PM PF 1,而 PM PF的最小值是MF 34
146、 P O P 4, 2 当 离圆 最远时 最小,此时点 坐标为: 记 APO ,
9
则 cos 1 2sin
2 ,计算得 cos =10
147、
2
n (n 1) (n 2) ,
k k 1 y 1 y 1 1 x
2
2
M MB MD
y 1
148、设点 的坐标为 (x, y),∵ 2 ,∴ x x 2 . 整理,得 2 ( x 0),
发现动点 M 的轨迹方程是椭圆,其焦点恰为 A,C 两点,所以MA MC 2 2
149、 0, 5
1
150、VA BCD (S1 S2 S3 S4 )r在四面体 A BCD中,四面体的体积V3 A BCD
可分成四个小三棱锥的
体积之和,而这四个小三棱锥的高都为内接球的半径 r ,底面积分别为 S1 、 S2 、 S3 、 S4 ,因此
V 1A BCD (S1 S2 S3 S4 )r3
151、 y2 8x
t 2 1(t 5)
152、9 y 2t 1(5 t 8) ,t= 8
8t 1(t 8)
3
153、
4
第58页,共66页
高中数学填空题专练
154、 5
m 1
1 2 2 3 m 5
155、4 m 4
m 1 3 m 5
2 3 2
156、 , 0 1 , 3
[ 1157、 , 3]
2 2
2
158、
5
1
159、
4
160、48;
161、-1
162、9
163、100
10
164、 7
7
165、50
166、45
167、180
2 a k a
f (x) 2 x k , 2168、 2 b k b由于 在 上是减函数,所以 关于 x的方程 2 x k x
k 2, 9 , 2 4 在 上有两个不同实根。通过换元结合图象可得
第59页,共66页
高中数学填空题专练
3
169、
6
170、 3;
171、 29 ;
172、 3 4 a 2.
173、-5;
174、 1
175、①③④
176、
177、 9
178、{x | 1 x 2};
179、 3n 1;
180、②④
181、 -1,-2
182、 2
183、 4,5 ;
184、②④
185、1
第60页,共66页
高中数学填空题专练
186、 -42
187、2
70
188、-
3
189、6
190、-2
191、69
192、 3
4 2 2
193、 ln 2
3
194、40
5
195、A.
2
B. (1, )
48
C.
5
196、 x | 0 x 2 ;
197、16;
4
198、 ;
3
199、 , 0 1 ,
3
第61页,共66页
高中数学填空题专练
200、85 ,1.6
201、4
202、
203、
204、 9
205、
206、2
207、(-1,1)
208、2
(1209、 ,1) ; 2012
2
210、1/4
211、12 .部分提示:
212、600;4
213、 (1,0)
214、28,640
1
215、 ( ,1) ; 2012
2
第62页,共66页
高中数学填空题专练
216、
217、0.7
218、 1 , 23 5
219、 6.
5 1
220、 .
2
221、 1
1
222、
3
223、 2
224、
225、 40
3 2
226、 1
2
227、60
228、3
229、14 ;
230、 2 ;
231、 chx chy shx shy.
232、1
233、61
第63页,共66页
高中数学填空题专练
x2. y
2
234、 + =1.
16 8
235、③, ④
236、84 乙
237、 y=0.7x+0.35
2 3
238、 3
239、 2(π 3)
240、 37
1
241、 x = ;2
2
242、 13
243、(1)7
(2)2n 1
5 -1
244、 (1)
2
- 5 5(2) ,
4 4
245、 x (0, ), tan x sin x
2
246、 2 .
247、 x2 8y
第64页,共66页
高中数学填空题专练
1
248、
3
249、(1)81(2)1004
250、 (-∞, 1〕
1 1
251、 , 4 2
252、 4.
253、8
254、 5 1
255、 0,
256、6
257、 3
1
258、
4
259、4
5
260、 或
6 6
6
261、
6
9
262、
8
263、 2, 3
第65页,共66页
高中数学填空题专练
264、 54 解:甲、乙两人得分的中位数之和是 28 26 54 .
1
265、【答案】 ( , )
2
x 2y 1 0,
【解析】作出不等式组 的平面区域, 由线性规划知识得最优解 (3,2) ,故 z 3x y的最
| x | y 1 0
大值为 7
266、【答案】 (1,3)
1
【解析】∵ | x | 2 ,∴ | a 2 | 1 2 ,即 | a 2 | 1,解得1 a 3 .
x
267、1
第66页,共66页
同课章节目录
