4.2正比例和反比例 课件(共21张PPT)-2021-2022学年数学六年级下册
文档属性
| 名称 | 4.2正比例和反比例 课件(共21张PPT)-2021-2022学年数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
之 正 比 例
第 4 单元 比例
4.2、 正比例和反比例
假设文具店有一种铅笔,其销售数量与总价的关系如下表:
数量/m 1 2 3 4 5 6 7 8 …
总价/元 4 8 12 16 15 24 28 32 …
观察上表,回答下面的问题:
(1)表中有几种变量?
数量、总价。
(2)总价是怎样随着数量的变化而变化的?
总价随着数量的增加而增加。
(3)相应的总价与数量的比分别是多少?比值是多少?
相应的比均为:4:1 比值均为4
一、探索新知
1
你能发现了什么?
从上表可以看出,总价与数量是两种相关联的量,总价是随着数量的变化而变化的,而且总价与相应数量的比值总是一定的。
例如: = = =…=3.5
4
1
8
2
12
3
比值4,实际就是铅笔的单价,用式子表示它们的关系是:
总价
数量
=单价
像这样,有两个相关的量:一个量变化,另一个也变化。如果两个量中相应的两个数之比是确定的,则称这两个量为正比例量,其关系称为正比例关系
在上表得知,总价与数量呈正比例关系。如果用字母y、X表示两个相关的量,用z表示它们的比例(一定),则正比例关系可以通过下式表示:
y
x
—
z(一定)=
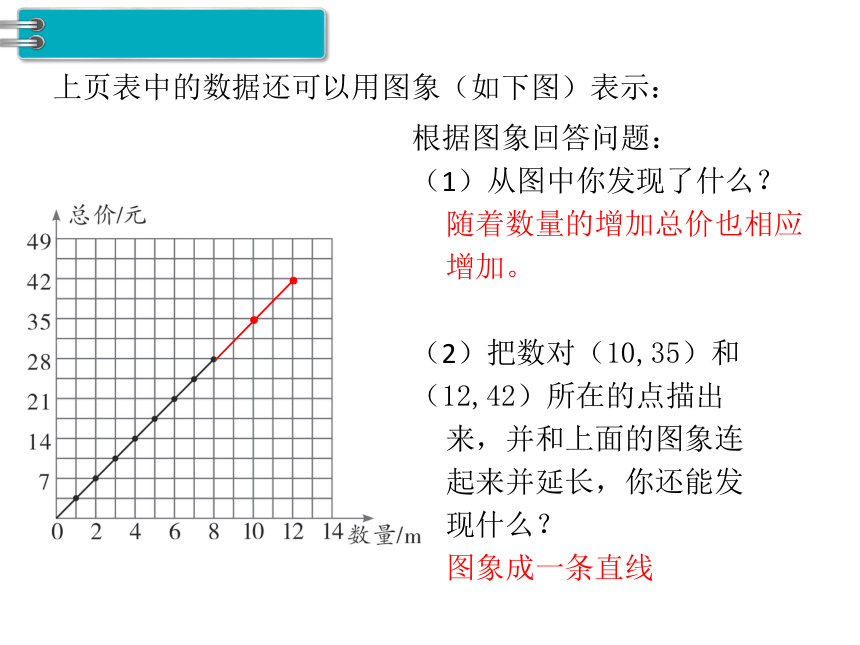
上页表中的数据还可以用图象(如下图)表示:
根据图象回答问题:
(1)从图中你发现了什么?
随着数量的增加总价也相应
增加。
(2)把数对(10,35)和(12,42)所在的点描出
来,并和上面的图象连
起来并延长,你还能发
现什么?
图象成一条直线
(3)根据图象判断,如果买9支铅笔,总价是多少?54
元能买多少支铅笔?
由图象可知9支铅笔的总价是36元。
54元能买6支铅笔。
(4)小光买的铅笔数是小丽的3倍,他花的钱是小丽的多少倍?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
生活中有正比例关系的例子吗?你能举个例子吗
3倍
二、巩固练习
一辆卡车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 70 140 210 280 350 420
(1)写出几组路程与时间的比,并比较比值的大小。
70:1=140:2=210:3=280:4=350:5=420:6
(2)这个比值表示什么呢?
这个比值表示速度。
(3)卡车行驶的路程与时间成正比例关系吗?说说你的理由
成正比例关系,因为路程与时间的比值一定。
满足以下三个条件的两种量,可称它们成正比例关系:
一、这两种量是相关联的量;
二、一种量变化,另一种量也随着变化;
三、这两种量中相对应的两个数的比值一定。
三、课堂小结
四、拓展训练
1.判断:圆的周长与半径成正比例。 (是 )
2.简答:圆的面积和圆的哪个量成正比例?
圆的面积和圆半径的平方成正比例。
之 反 比 例
4.2 正比例和反比例
一、复习导入
判断下面各题中的两种量是否成正比例。
1.长方形的长一定,它的宽和面积;
不成比例
2.圆的周长和半径;
成正比例
3.一个人的年龄和他的身高。
不成比例
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm2 10 15 20 30 60 …
水的高度/cm 60 40 30 20 10 …
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)随着杯子底面积的大小变化,水的高度是怎样变化的?
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
二、探索新知
2
从上表可以看出,水的高度和杯底面积是两个相关的量,水的高度随着杯底面积的增加而减小。水的高度和杯子底部面积的乘积总是确定的。例如:60×10=40×15=30×20=…=600。
积600,实际就是倒入杯子的水的体积。用式子表示它们的关系就是:
底面积×高度=体积
这样,两个相关的量,一个变化,另一个也变化。如果两个量中对应的两个数的乘积是确定的,则称这两个量为反比例的量,称它们的关系为反比关系。在上面的实验中,高度和底面积是成反比例的量,高度与底面积成反比例关系。
如果用字母x和y表示两种相关联的量,用z表示它们的积(一定),那么反比例关系可以用下面的式子表示:
z(一定)=xy
比较例1
和例2,
小组讨论
正反比例
的相同点
和不同点,
并归纳填
空。
相关联
变化
变化
比值
积
y
x
x
y
k
k
如果总价一定,单价与数量成反比例关系。
如果长方形的面积一定,它的长与宽成反比例关系。
举出生活中反比例关系的例子
三、巩固练习
每天运的吨数/t 600 300 200 150 120 100
运货的天数/天 1 2 3 4 5 6
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和运货的天数两种相关联的量。
(2)写出几组这两种量中相对应的两个数的积,并比较积的大
小,说一说这个积表示什么。
600×1=300×2=200×3=150×4=120×5=100×6=600,
积表示需要运输货物的总吨数。
(3)每天运的吨数与运货的天数成反比例关系吗?为什么?
成反比例关系,因为每天运的吨数与运货的天数的乘积一定。
(1)煤的总量一定,每天的烧煤量和能够烧的天数.
判断下面每题中的两种量是不是成反比例,并说明理由.
因为
所以
每天的烧煤量和能够烧的天数成反比例.
每天烧煤的量×烧的天数=煤的总量(一定)
因为
所以
(2)种子的总量一定,每公顷的播种量和播种的公顷数.
每公顷的播种量×播种的公顷数=种子总量(一定)
每公顷的播种量和播种的公顷数成反比例.
因为
所以
(3)李叔叔从家到工厂,骑自行车的速度和所需的时间.
自行车的速度×所需的时间=路程(一定)
骑自行车的速度和所需的时间成反比例.
之 正 比 例
第 4 单元 比例
4.2、 正比例和反比例
假设文具店有一种铅笔,其销售数量与总价的关系如下表:
数量/m 1 2 3 4 5 6 7 8 …
总价/元 4 8 12 16 15 24 28 32 …
观察上表,回答下面的问题:
(1)表中有几种变量?
数量、总价。
(2)总价是怎样随着数量的变化而变化的?
总价随着数量的增加而增加。
(3)相应的总价与数量的比分别是多少?比值是多少?
相应的比均为:4:1 比值均为4
一、探索新知
1
你能发现了什么?
从上表可以看出,总价与数量是两种相关联的量,总价是随着数量的变化而变化的,而且总价与相应数量的比值总是一定的。
例如: = = =…=3.5
4
1
8
2
12
3
比值4,实际就是铅笔的单价,用式子表示它们的关系是:
总价
数量
=单价
像这样,有两个相关的量:一个量变化,另一个也变化。如果两个量中相应的两个数之比是确定的,则称这两个量为正比例量,其关系称为正比例关系
在上表得知,总价与数量呈正比例关系。如果用字母y、X表示两个相关的量,用z表示它们的比例(一定),则正比例关系可以通过下式表示:
y
x
—
z(一定)=
上页表中的数据还可以用图象(如下图)表示:
根据图象回答问题:
(1)从图中你发现了什么?
随着数量的增加总价也相应
增加。
(2)把数对(10,35)和(12,42)所在的点描出
来,并和上面的图象连
起来并延长,你还能发
现什么?
图象成一条直线
(3)根据图象判断,如果买9支铅笔,总价是多少?54
元能买多少支铅笔?
由图象可知9支铅笔的总价是36元。
54元能买6支铅笔。
(4)小光买的铅笔数是小丽的3倍,他花的钱是小丽的多少倍?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
生活中有正比例关系的例子吗?你能举个例子吗
3倍
二、巩固练习
一辆卡车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 70 140 210 280 350 420
(1)写出几组路程与时间的比,并比较比值的大小。
70:1=140:2=210:3=280:4=350:5=420:6
(2)这个比值表示什么呢?
这个比值表示速度。
(3)卡车行驶的路程与时间成正比例关系吗?说说你的理由
成正比例关系,因为路程与时间的比值一定。
满足以下三个条件的两种量,可称它们成正比例关系:
一、这两种量是相关联的量;
二、一种量变化,另一种量也随着变化;
三、这两种量中相对应的两个数的比值一定。
三、课堂小结
四、拓展训练
1.判断:圆的周长与半径成正比例。 (是 )
2.简答:圆的面积和圆的哪个量成正比例?
圆的面积和圆半径的平方成正比例。
之 反 比 例
4.2 正比例和反比例
一、复习导入
判断下面各题中的两种量是否成正比例。
1.长方形的长一定,它的宽和面积;
不成比例
2.圆的周长和半径;
成正比例
3.一个人的年龄和他的身高。
不成比例
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm2 10 15 20 30 60 …
水的高度/cm 60 40 30 20 10 …
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)随着杯子底面积的大小变化,水的高度是怎样变化的?
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
二、探索新知
2
从上表可以看出,水的高度和杯底面积是两个相关的量,水的高度随着杯底面积的增加而减小。水的高度和杯子底部面积的乘积总是确定的。例如:60×10=40×15=30×20=…=600。
积600,实际就是倒入杯子的水的体积。用式子表示它们的关系就是:
底面积×高度=体积
这样,两个相关的量,一个变化,另一个也变化。如果两个量中对应的两个数的乘积是确定的,则称这两个量为反比例的量,称它们的关系为反比关系。在上面的实验中,高度和底面积是成反比例的量,高度与底面积成反比例关系。
如果用字母x和y表示两种相关联的量,用z表示它们的积(一定),那么反比例关系可以用下面的式子表示:
z(一定)=xy
比较例1
和例2,
小组讨论
正反比例
的相同点
和不同点,
并归纳填
空。
相关联
变化
变化
比值
积
y
x
x
y
k
k
如果总价一定,单价与数量成反比例关系。
如果长方形的面积一定,它的长与宽成反比例关系。
举出生活中反比例关系的例子
三、巩固练习
每天运的吨数/t 600 300 200 150 120 100
运货的天数/天 1 2 3 4 5 6
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和运货的天数两种相关联的量。
(2)写出几组这两种量中相对应的两个数的积,并比较积的大
小,说一说这个积表示什么。
600×1=300×2=200×3=150×4=120×5=100×6=600,
积表示需要运输货物的总吨数。
(3)每天运的吨数与运货的天数成反比例关系吗?为什么?
成反比例关系,因为每天运的吨数与运货的天数的乘积一定。
(1)煤的总量一定,每天的烧煤量和能够烧的天数.
判断下面每题中的两种量是不是成反比例,并说明理由.
因为
所以
每天的烧煤量和能够烧的天数成反比例.
每天烧煤的量×烧的天数=煤的总量(一定)
因为
所以
(2)种子的总量一定,每公顷的播种量和播种的公顷数.
每公顷的播种量×播种的公顷数=种子总量(一定)
每公顷的播种量和播种的公顷数成反比例.
因为
所以
(3)李叔叔从家到工厂,骑自行车的速度和所需的时间.
自行车的速度×所需的时间=路程(一定)
骑自行车的速度和所需的时间成反比例.
