1.2.2空间立体几何的三视图

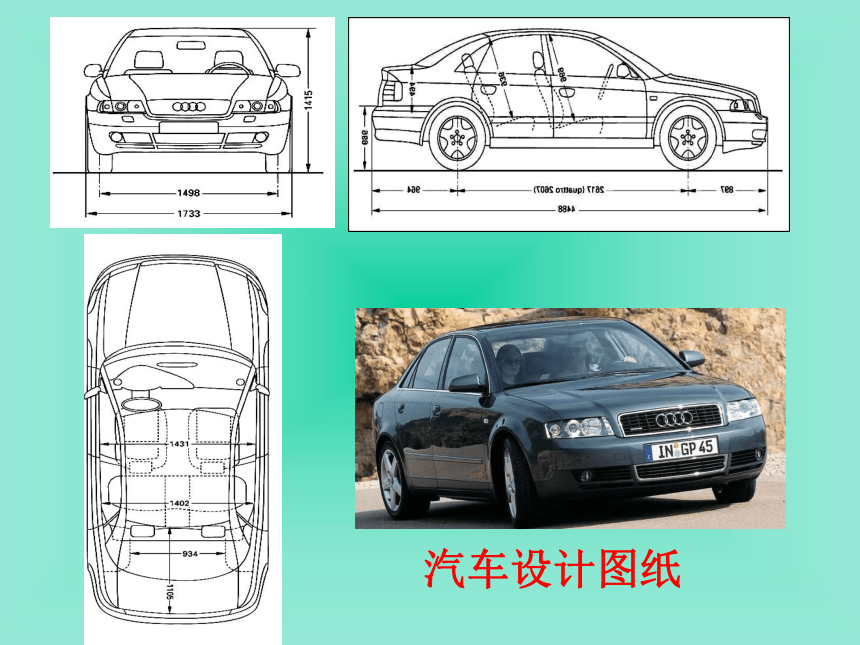
课件34张PPT。汽车设计图纸题西林壁宋 苏轼横看成岭侧成峰；远近高低各不同。不识庐山真面目；只缘身在此山中。引 入诗中描写了哪些视图？从不同的角度看同一物体,视觉的效果可能不同，
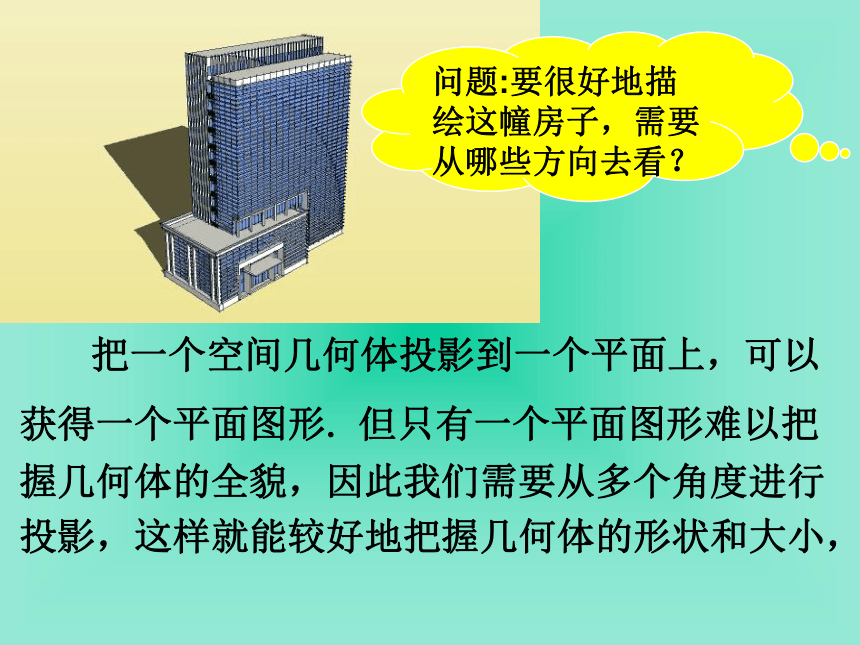
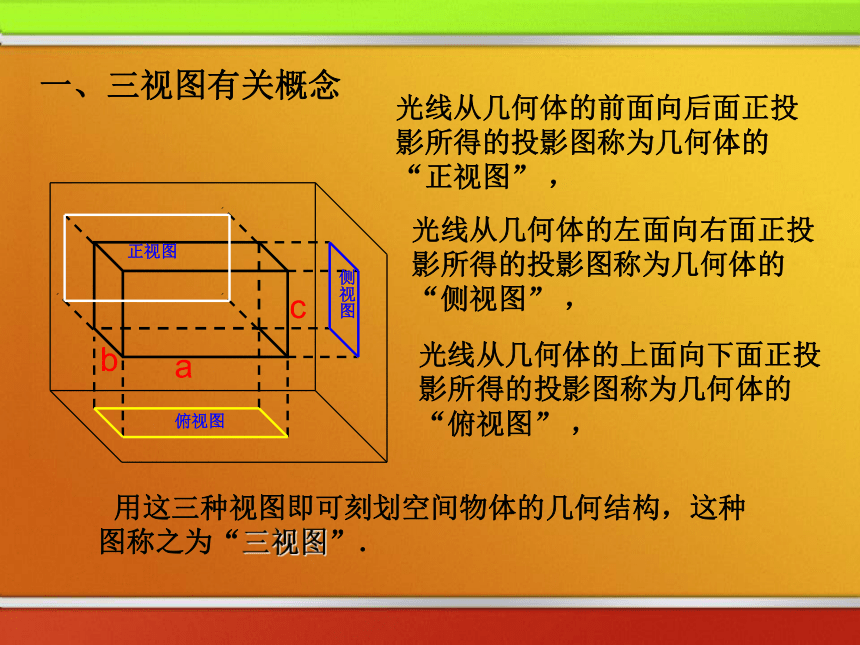
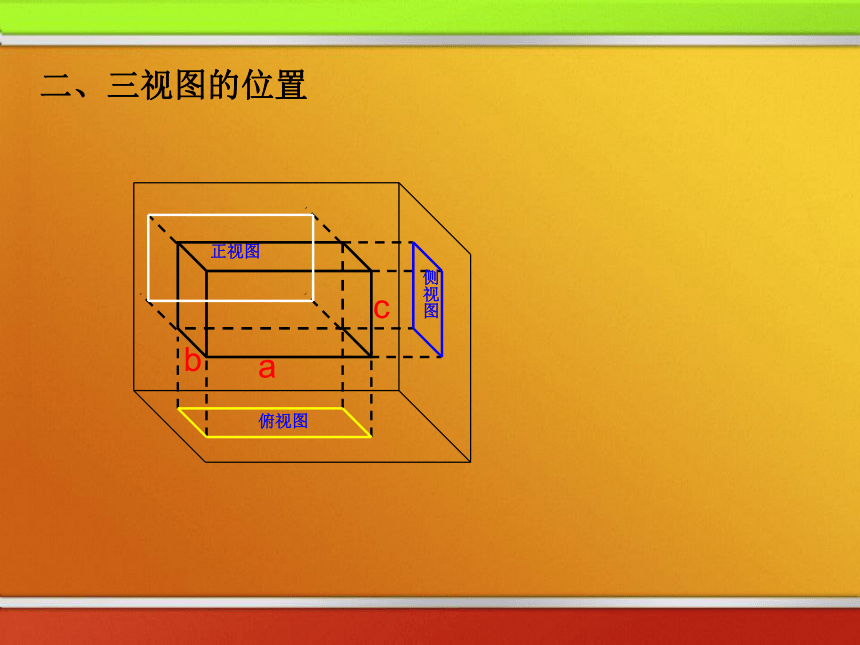
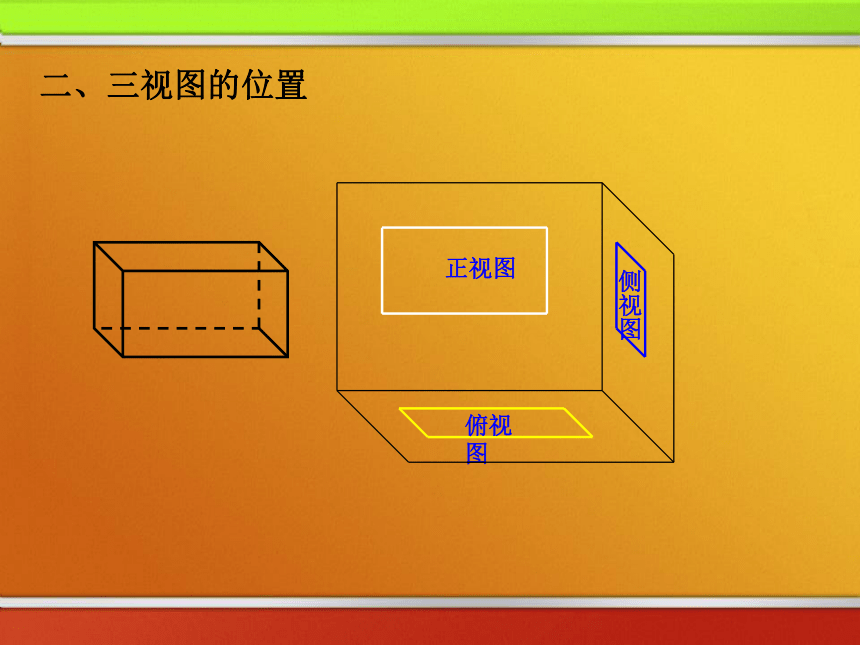
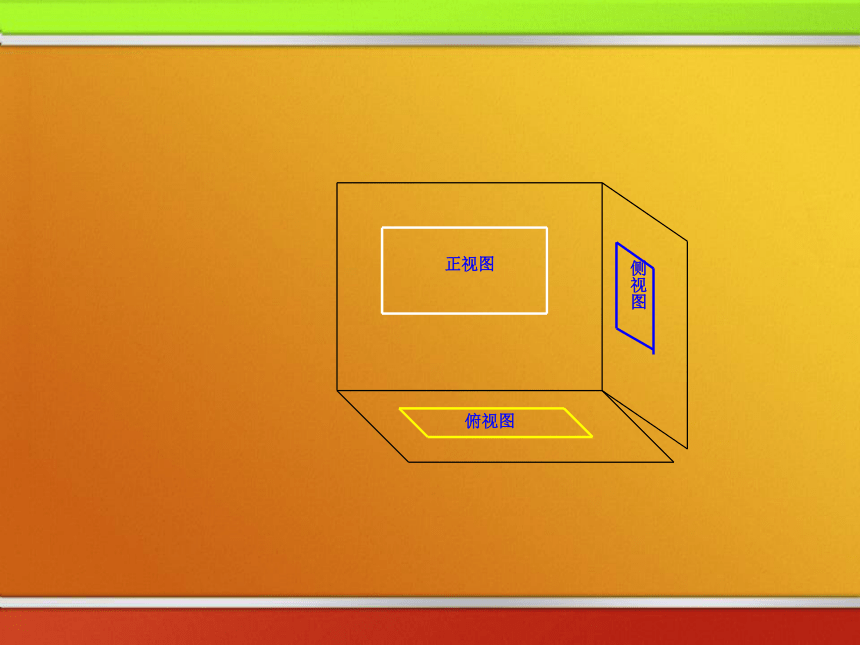
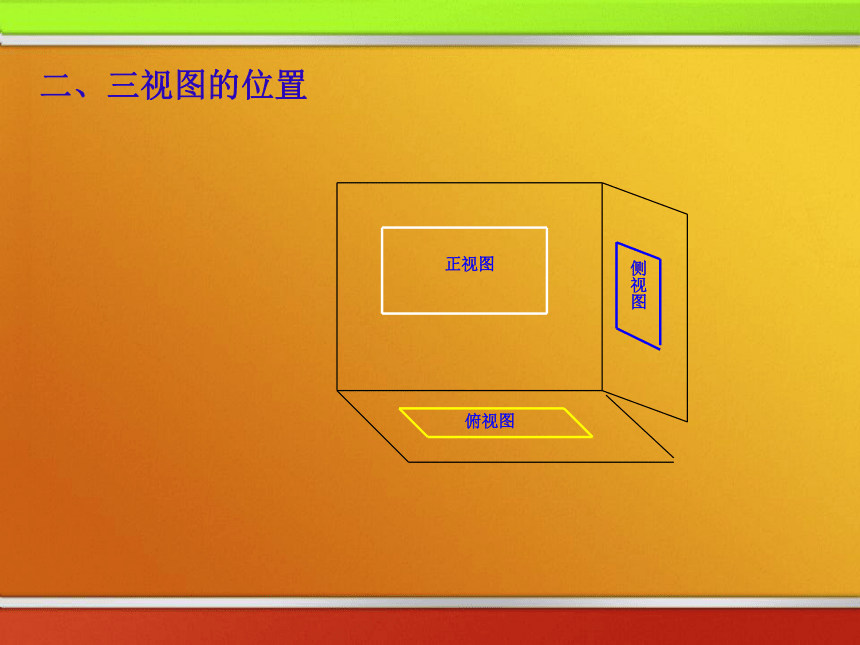
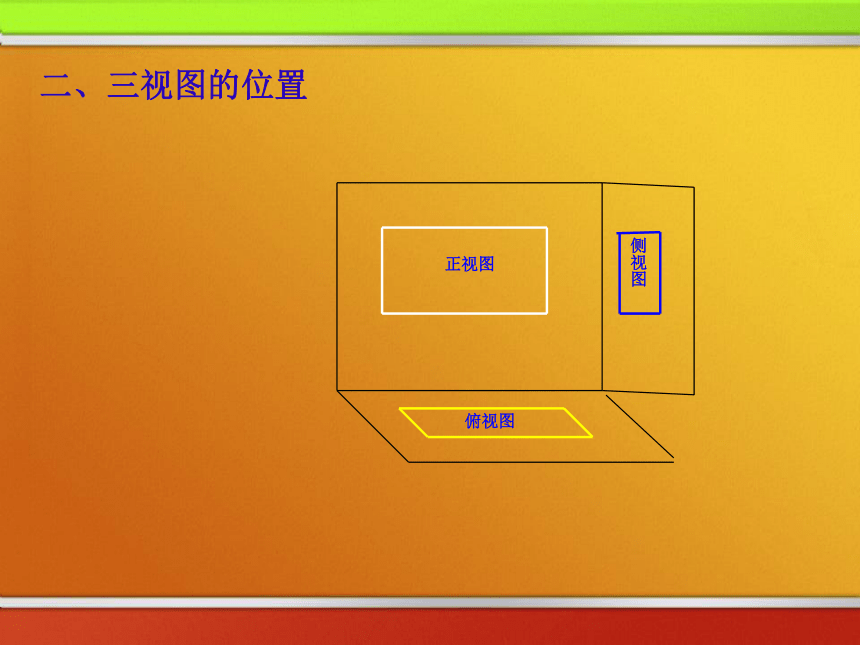
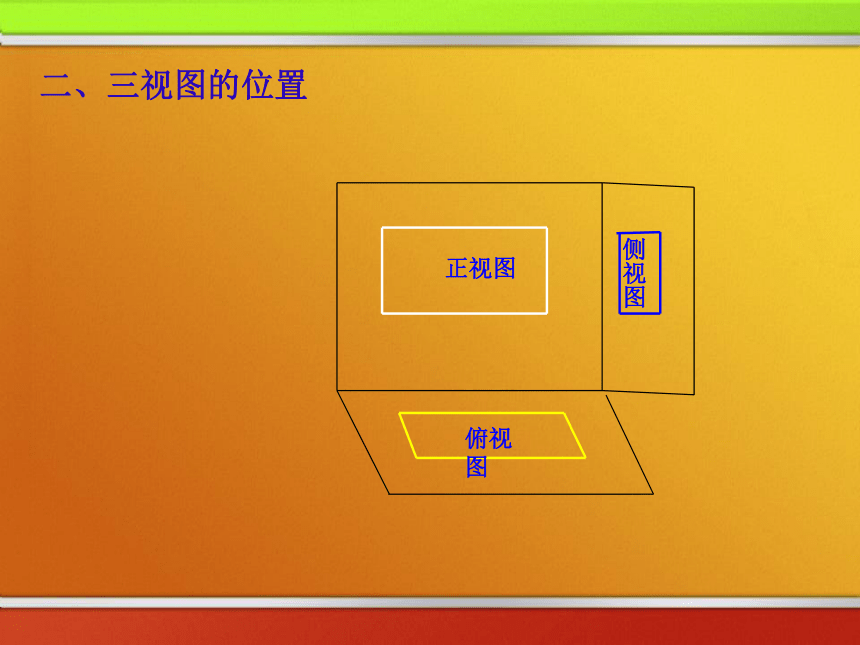
要比较真实地反映出物体的特征我们可从多角度观看物体。问题:要很好地描绘这幢房子，需要从哪些方向去看？ 把一个空间几何体投影到一个平面上，可以获得一个平面图形. 但只有一个平面图形难以把握几何体的全貌，因此我们需要从多个角度进行投影，这样就能较好地把握几何体的形状和大小，空间几何体的三视图俯视图光线从几何体的前面向后面正投影所得的投影图称为几何体的“正视图” ，正视图侧视图一、三视图有关概念光线从几何体的左面向右面正投影所得的投影图称为几何体的“侧视图” ，光线从几何体的上面向下面正投影所得的投影图称为几何体的“俯视图” ， 用这三种视图即可刻划空间物体的几何结构，这种图称之为“三视图”．二、三视图的位置俯视图正视图侧视图二、三视图的位置侧视图俯视图正视图正视图侧视图俯视图二、三视图的位置正视图侧视图俯视图二、三视图的位置正视图侧视图俯视图二、三视图的位置正视图侧视图俯视图二、三视图的位置上正，右侧，下俯. 三、三视图之间的投影规律 :
想一想长方体的三视图分别反映了哪些方面的特征？正视图反映了长方体的高度和长度侧视图反映了长方体的高度和宽度俯视图反映了长方体的长度和宽度 c（高） a(长) b（宽） 正视图 侧视图 俯视图 长对正 高平齐 宽相等 正视图与俯视图的长相等，且相互对正,正视图与侧视图的高度相等，且相互对齐，俯视图与侧视图的宽度相等， 类比长方体，想一想一个几何体的三视图的长度、宽
度和高度有什么关系？例1：下面各图中物体形状分另可以看成什么样的几何体? 圆柱 圆锥 球从正面,侧面,上面看这些几何体,它们的形状各是什么样的?正面看:长方形 等腰三角形 圆侧面看:长方形 等腰三角形 圆上面看: 圆 圆 圆你能画出各物体的三视图吗?四、有几何体想三视图正视图侧视图俯视图正视图侧视图俯视图圆柱、圆锥三视图正视图侧视图俯视图球的三视图例2：请同学们画下面这两个圆台的三视图，如果你认为这两个圆台的三视图一样，画一个就可以；如果你认为不一样，请分别画出来。注意：
(1)画几何体的三视图时，
能看见的轮廓和棱用实线表示，
不能看见的轮廓和棱用虚线表示。

(2)长对正， 高平齐， 宽相等。例3：画出下列几何体的三视图例3（变式思考）例3（变式思考）例3（变式思考）看得见部分的轮廓线画实线,
看不见部分的轮廓线画虚线.
例3（变式思考2）例3（变式思考3）例3（变式思考）五、由三视图画出几何体ACBD1.下图中的三视图表示下面哪个几何体？俯视图侧视图正视图2. 下列三视图所表示的几何体是
.练习正视图侧视图俯视图2. 下列三视图所表示的几何体是
.练习一个四棱台 正视图侧视图俯视图例4正视图俯视图侧视图（变式思考4 ）例4（变式思考4 ）正视图侧视图俯视图长对正,宽相等,高平齐.规则看得见部分的轮廓线画实线,看不见部分的轮廓线画虚线.
注意上正,右侧下俯位置总结三视图:
正视图——从正面看到的图
侧视图——从左面看到的图
俯视图——从上面看到的图物体的三视图时，要符合如下原则: