圆的一般方程
图片预览











文档简介
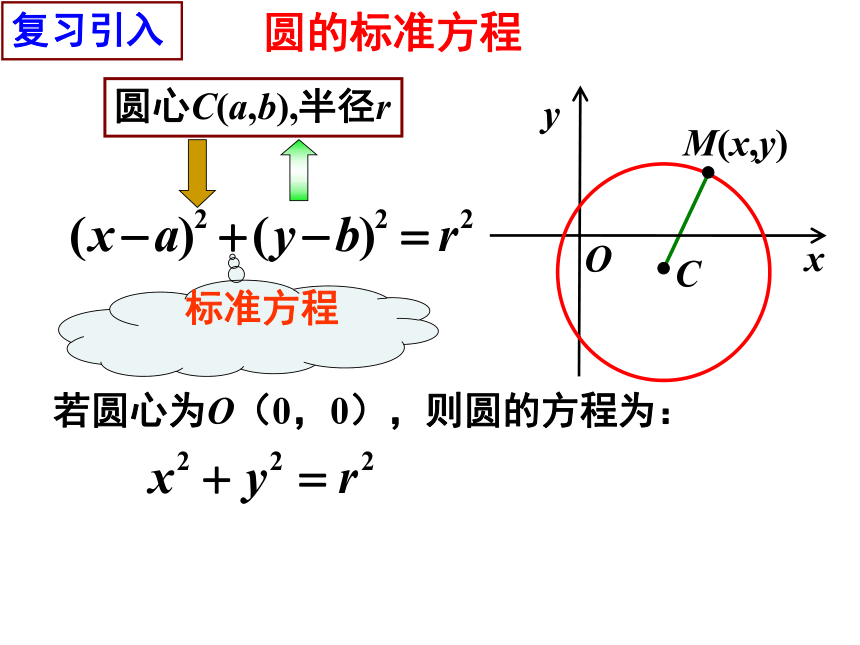
课件30张PPT。圆的标准方程xyOCM(x,y)圆心C(a,b),半径r若圆心为O(0,0),则圆的方程为:标准方程
复习引入圆心 (2, -4) ,半径 (1) 圆 (x-2)2+ (y+4)2=2(2) 圆 (x+1)2+ (y+2)2=m2圆心 (-1, -2) ,半径|m|(m≠0)分别说出下列圆的圆心与半径复习引入4.1.2 圆的一般方程圆的方程一般代数形式是什么特点呢展开得任何一个圆的方程都是二元二次方程- a- br2-2ax-2by+a2+b2-r2=0思考结论:任何一个圆方程可以写成下面形式:结论:任何一个圆方程可以写成下面形式: x2 +y 2+Dx+Ey+F=0探究:是不是任何一个形如
x2 +y 2+Dx+Ey+F=0 方程表示
的曲线是圆呢?配方得不一定是圆以(1,-2)为圆心,以2为半径的圆配方得不是圆思考圆的一般方程(1)当 时,表示圆,(2)当 时,表示点(3)当 时,不表示任何图形【排忧解惑】圆心·圆的一般方程其中D2+E2-4F>0 思考:圆的标准方程与圆的一般方程各有什么特点?(1)形式不同:(x-a)2+(y-b)2=r2
x2+y2+Dx+Ey+F=0(2)圆的一般方程的特点:
(a)x2 , y2 的系数为1(b)没有x y项(c)D2 +E2 -4F>0练习:课本123页1,2解 由方程表示圆得,
D2+E2-4F=12+22-4(a-1)=9-4a>0,
解得a< ,
即a的取值范围是 .例4:求过三点A(5,1),B (7,-3),C(2,-8)的圆的方程圆心:两条弦的中垂线的交点半径:圆心到圆上一点xyOEA(5,1)B(7,-3)C(2,-8)几何方法方法一:方法二:待定系数法
待定系数法解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,8)都在圆上所求圆的方程为方法三:待定系数法
解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,-8)都在圆上所求圆的方程为(1)若已知条件涉及圆心和半径,我们一般采用圆的标准方程较简单.圆的一般方程与圆的标准方程在应用上的比较练习:(2).若已知三点求圆的方程,我们常采用圆的一般方程用待定系数法求解. 圆的一般方程与圆的标准方程在运用上的比较练习:把点A,B,C的坐标代入得方程组所求圆的方程为:名师点睛2.求圆的一般方程
(1)求圆的方程时,若已知条件中明确圆心的坐标或半径,则设圆的标准方程求解;若已知条件中没有明确圆心坐标或半径大小,则设圆的一般方程求解.
(2)由于圆的一般方程中所含的三个待定系数不是二次项的系数,在由三个独立条件列出方程组后,一般可求出待定系数D,E,F.
(3)若求圆心和半径,则可以将圆的一般方程配方成圆的标准方程,再写出圆心坐标和半径.另外在解答圆的有关问题时,应注意利用圆的平面几何的性质,使运算简化.
练习:课本123页3解 设动点P的坐标为(x,y),
则点P(x,y)满足 ,
即 ,
化简得x2+y2+2x-3=0.即(x+1)2+y2=4,
所以动点P的轨迹是以点(-1,0)为圆心,以2为半径的圆.小结:求圆的方程几何方法求圆心坐标 (两条直线的交点)(常用弦的中垂线) 求 半径
(圆心到圆上一点距离) 写出圆的标准方程待定系数法列关于a,b,r(或D,E,F)的方程组解出a,b,r(或D,E,F),写出标准方程(或一般方程)活页规范训练解析 由圆心(1,2)到直线的距离公式得
得a=0或a=2.故选C.
答案 C2.若圆x2+y2-2x-4y=0的圆心到直线x-y+a=0的距离为 ,则a的值为( ).
A.-2或2 B. 或 C.2或0D.-2或0解析 圆心 在直线y=x+1上,
所以 ,
m=-3.
答案 C3.已知圆x2+y2-mx+y=0始终被直线y=x+1平分,则m的值为( ).
A.0 B.1 C.-3 D.34.(2012·合肥高一检测)设直线2x+3y+1=0和圆x2+y2-2x-3=0相交于点A,B,则弦AB的垂直平分线方程是________________.
解析 由圆x2+y2-2x-3=0,可得(x-1)2+y2=4.
圆心坐标为(1,0),
kAB= ,∴AB垂直平分线的斜率为 .
从而由点斜式,得y-0= (x-1).
∴直线方程为3x-2y-3=0.
答案 3x-2y-3=05.设圆x2+y2-4x+2y-11=0的圆心为A,点P在圆上,则PA的中点M的轨迹方程是________.
解析 将x2+y2-4x+2y-11=0配方,
得(x-2)2+(y+1)2=16,
则圆心A(2,-1),
设PA的中点M(x,y),则P(2x-2,2y+1),
代入方程x2+y2-4x+2y-11=0,
化简,得x2+y2-4x+2y+1=0.
答案 x2+y2-4x+2y+1=07.如果圆的方程为x2+y2+kx+2y+k2=0,那么当圆的面积最大时,圆心坐标为( ).
A.(-1,1) B.(1,-1)
C.(-1,0) D.(0,-1)
解析 ∵x2+y2+kx+2y+k2=0,
∴ ,
∵k2=0时面积最大,∴圆心坐标为(0,-1).
答案 D11.(2012·菏泽学院附中高一检测)已知Rt△ABC中,A(-1,0),B(3,0),求(1)直角顶点C的轨迹方程;
解 (1)设C(x,y),
则kAC= ,kBC= .
∵AC⊥BC,∴kAC·kBC=-1,
即 · =-1,
化简得x2+y2-2x-3=0.
由于A、B、C不共线,∴y≠0.
故顶点C的轨迹方程为
x2+y2-2x-3=0(y≠0).11.(2012·菏泽学院附中高一检测)已知Rt△ABC中,A(-1,0),B(3,0),求 (2)直角边BC的中点M的轨迹方程.
解 (2)设M(x,y),C(x1,y1),
由(1)知(x1-1)2+y=4(y≠0).①
又B(3,0),M为BC中点,
由中点坐标公式,
知x= ,y= ,
即x1=2x-3,y1=2y.
代入①式,得中点M的轨迹方程为
(2x-4)2+(2y)2=4,
即(x-2)2+y2=1(y≠0).
复习引入圆心 (2, -4) ,半径 (1) 圆 (x-2)2+ (y+4)2=2(2) 圆 (x+1)2+ (y+2)2=m2圆心 (-1, -2) ,半径|m|(m≠0)分别说出下列圆的圆心与半径复习引入4.1.2 圆的一般方程圆的方程一般代数形式是什么特点呢展开得任何一个圆的方程都是二元二次方程- a- br2-2ax-2by+a2+b2-r2=0思考结论:任何一个圆方程可以写成下面形式:结论:任何一个圆方程可以写成下面形式: x2 +y 2+Dx+Ey+F=0探究:是不是任何一个形如
x2 +y 2+Dx+Ey+F=0 方程表示
的曲线是圆呢?配方得不一定是圆以(1,-2)为圆心,以2为半径的圆配方得不是圆思考圆的一般方程(1)当 时,表示圆,(2)当 时,表示点(3)当 时,不表示任何图形【排忧解惑】圆心·圆的一般方程其中D2+E2-4F>0 思考:圆的标准方程与圆的一般方程各有什么特点?(1)形式不同:(x-a)2+(y-b)2=r2
x2+y2+Dx+Ey+F=0(2)圆的一般方程的特点:
(a)x2 , y2 的系数为1(b)没有x y项(c)D2 +E2 -4F>0练习:课本123页1,2解 由方程表示圆得,
D2+E2-4F=12+22-4(a-1)=9-4a>0,
解得a< ,
即a的取值范围是 .例4:求过三点A(5,1),B (7,-3),C(2,-8)的圆的方程圆心:两条弦的中垂线的交点半径:圆心到圆上一点xyOEA(5,1)B(7,-3)C(2,-8)几何方法方法一:方法二:待定系数法
待定系数法解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,8)都在圆上所求圆的方程为方法三:待定系数法
解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,-8)都在圆上所求圆的方程为(1)若已知条件涉及圆心和半径,我们一般采用圆的标准方程较简单.圆的一般方程与圆的标准方程在应用上的比较练习:(2).若已知三点求圆的方程,我们常采用圆的一般方程用待定系数法求解. 圆的一般方程与圆的标准方程在运用上的比较练习:把点A,B,C的坐标代入得方程组所求圆的方程为:名师点睛2.求圆的一般方程
(1)求圆的方程时,若已知条件中明确圆心的坐标或半径,则设圆的标准方程求解;若已知条件中没有明确圆心坐标或半径大小,则设圆的一般方程求解.
(2)由于圆的一般方程中所含的三个待定系数不是二次项的系数,在由三个独立条件列出方程组后,一般可求出待定系数D,E,F.
(3)若求圆心和半径,则可以将圆的一般方程配方成圆的标准方程,再写出圆心坐标和半径.另外在解答圆的有关问题时,应注意利用圆的平面几何的性质,使运算简化.
练习:课本123页3解 设动点P的坐标为(x,y),
则点P(x,y)满足 ,
即 ,
化简得x2+y2+2x-3=0.即(x+1)2+y2=4,
所以动点P的轨迹是以点(-1,0)为圆心,以2为半径的圆.小结:求圆的方程几何方法求圆心坐标 (两条直线的交点)(常用弦的中垂线) 求 半径
(圆心到圆上一点距离) 写出圆的标准方程待定系数法列关于a,b,r(或D,E,F)的方程组解出a,b,r(或D,E,F),写出标准方程(或一般方程)活页规范训练解析 由圆心(1,2)到直线的距离公式得
得a=0或a=2.故选C.
答案 C2.若圆x2+y2-2x-4y=0的圆心到直线x-y+a=0的距离为 ,则a的值为( ).
A.-2或2 B. 或 C.2或0D.-2或0解析 圆心 在直线y=x+1上,
所以 ,
m=-3.
答案 C3.已知圆x2+y2-mx+y=0始终被直线y=x+1平分,则m的值为( ).
A.0 B.1 C.-3 D.34.(2012·合肥高一检测)设直线2x+3y+1=0和圆x2+y2-2x-3=0相交于点A,B,则弦AB的垂直平分线方程是________________.
解析 由圆x2+y2-2x-3=0,可得(x-1)2+y2=4.
圆心坐标为(1,0),
kAB= ,∴AB垂直平分线的斜率为 .
从而由点斜式,得y-0= (x-1).
∴直线方程为3x-2y-3=0.
答案 3x-2y-3=05.设圆x2+y2-4x+2y-11=0的圆心为A,点P在圆上,则PA的中点M的轨迹方程是________.
解析 将x2+y2-4x+2y-11=0配方,
得(x-2)2+(y+1)2=16,
则圆心A(2,-1),
设PA的中点M(x,y),则P(2x-2,2y+1),
代入方程x2+y2-4x+2y-11=0,
化简,得x2+y2-4x+2y+1=0.
答案 x2+y2-4x+2y+1=07.如果圆的方程为x2+y2+kx+2y+k2=0,那么当圆的面积最大时,圆心坐标为( ).
A.(-1,1) B.(1,-1)
C.(-1,0) D.(0,-1)
解析 ∵x2+y2+kx+2y+k2=0,
∴ ,
∵k2=0时面积最大,∴圆心坐标为(0,-1).
答案 D11.(2012·菏泽学院附中高一检测)已知Rt△ABC中,A(-1,0),B(3,0),求(1)直角顶点C的轨迹方程;
解 (1)设C(x,y),
则kAC= ,kBC= .
∵AC⊥BC,∴kAC·kBC=-1,
即 · =-1,
化简得x2+y2-2x-3=0.
由于A、B、C不共线,∴y≠0.
故顶点C的轨迹方程为
x2+y2-2x-3=0(y≠0).11.(2012·菏泽学院附中高一检测)已知Rt△ABC中,A(-1,0),B(3,0),求 (2)直角边BC的中点M的轨迹方程.
解 (2)设M(x,y),C(x1,y1),
由(1)知(x1-1)2+y=4(y≠0).①
又B(3,0),M为BC中点,
由中点坐标公式,
知x= ,y= ,
即x1=2x-3,y1=2y.
代入①式,得中点M的轨迹方程为
(2x-4)2+(2y)2=4,
即(x-2)2+y2=1(y≠0).
