2021-2022学年苏科版八年级上册数学第六章一次函数 单元过关检测(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级上册数学第六章一次函数 单元过关检测(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 455.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 10:53:26 | ||
图片预览




文档简介
(苏科版)2021-2022学年八年级(上册)数学
第六章 一次函数 单元过关检测
时间:120分钟满分:120分
一、单选题(共36分)
1.(本题3分)下列各函数中,是正比例函数的是( )
A. B.
C. D.
2.(本题3分)已知函数是一次函数,则的值为( )
A.1 B. C.0或 D.1或
3.(本题3分)在函数中,自变量的取值范围是( )
A. B. C. D.
4.(本题3分)如图是函数的图像,则点在( )象限内
A.第一 B.第二 C.第三 D.第四
5.(本题3分)以二元一次方程的解为坐标的点组成的图象画在坐标系中可能是( )
A. B.
C. D.
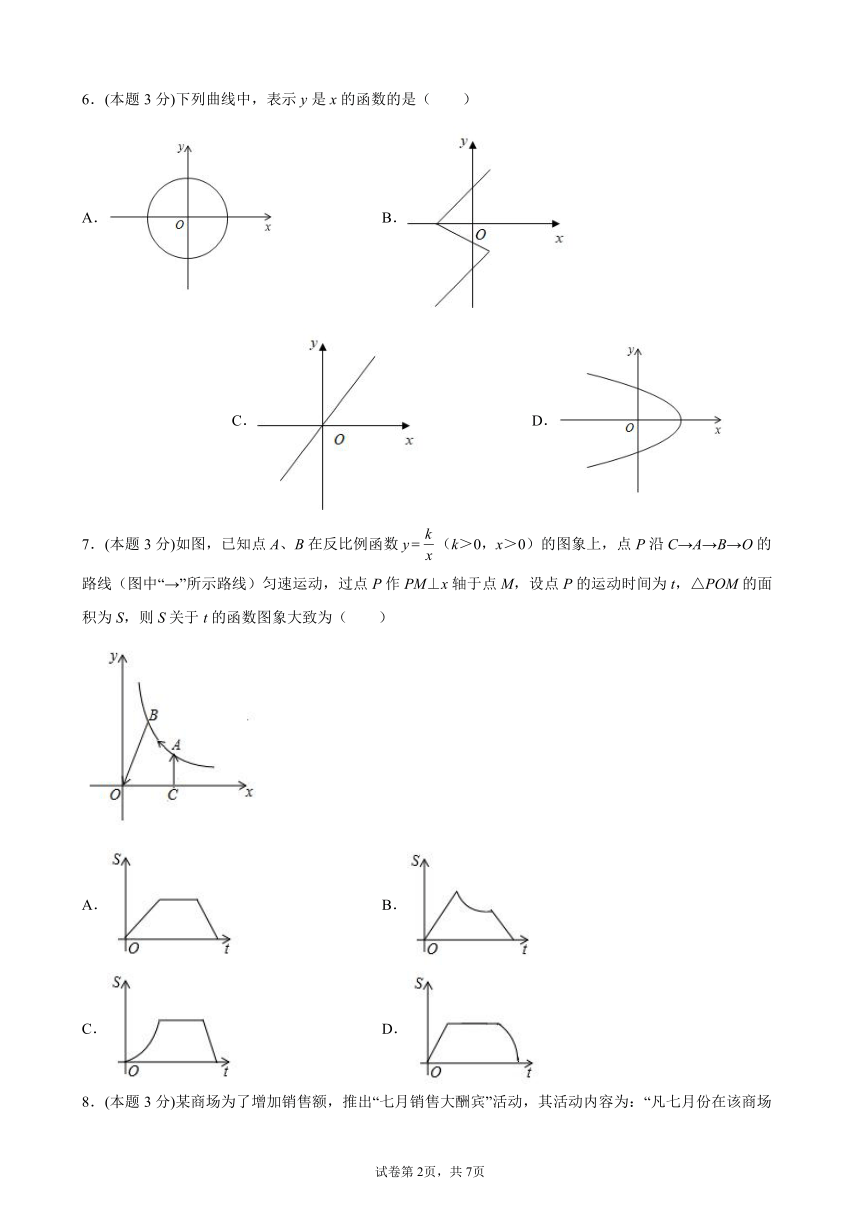
6.(本题3分)下列曲线中,表示y是x的函数的是( )
A. B. C. D.
7.(本题3分)如图,已知点A、B在反比例函数y(k>0,x>0)的图象上,点P沿C→A→B→O的路线(图中“→”所示路线)匀速运动,过点P作PM⊥x轴于点M,设点P的运动时间为t,△POM的面积为S,则S关于t的函数图象大致为( )
A. B.
C. D.
8.(本题3分)某商场为了增加销售额,推出“七月销售大酬宾”活动,其活动内容为:“凡七月份在该商场一次性购物超过100元以上者,超过100元的部分按9折优惠”.在大酬宾活动中,小王到该商场为单位购买单价为60元的办公用品x件(),则应付货款y(元)与商品件数x的函数关系式是( )
A. B.
C. D.
9.(本题3分)在某一阶段,某商品的销售量与销售价之间存在如下关系:设该商品的销售价为x元,售量为y件,估计当x=137时,y的值可能为( )
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
A.63 B.59 C.53 D.43
10.(本题3分)如图,一次函数的图象经过点,则下列结论正确的是( )
A.图像经过一、二、三象限 B.关于方程的解是
C. D.随的增大而减小
11.(本题3分)一次函数y=kx+b(k≠0)的图象如图所示,当x>2时,y的取值范围是( )
A.y<0 B.y>0 C.y<3 D.y>3
12.(本题3分)若直线和相交于点,则方程组的解为( )
A. B. C. D.
二、填空题(共30分)
13.(本题3分)已知自变量为x的函数y=mx+2-m是正比例函数,则m=_________ .
14.(本题3分)从中宁到银川的距离为130千米,一辆小轿车车以平均每小时80千米的速度从中宁出发到银川,则小轿车距银川的距离y(千米)与行驶时间x(时)的函数表达式为______.
15.(本题3分)函数中,的值随着值的增大而______,它的图象与轴的交点坐标是______.
16.(本题3分)已知y与成正比例,且当时,,则y与x之间的函数关系式为______________.
17.(本题3分)如图,函数和的图象相交于,则不等式的解集为____.
18.(本题3分)函数,则当函数自变量时,y=______
19.(本题3分)下列函数:①,②,③,④,⑤其中是一次函数的有_____.(填序号)
20.(本题3分)一次函数y=kx+b的图象如图所示,当x满足 _____时,y≥1.
21.(本题3分)已知函数y=(m﹣1)+2x+1为一次函数,则m=____.
22.(本题3分)一次函数的图象如图所示,则关于的不等式的解集为______.
三、解答题(共54分)
23.(本题5分)在正比例函数y=(k-3)x|k-3|中,函数值y随x的增大而减小,求k的值.
24.(本题6分)已知函数y=(2-m)x+2n-3.求当m为何值时.
(1)此函数为一次函数
(2)此函数为正比例函数
25.(本题6分)如图,已知两个一次函数y1=x﹣6和y2=﹣x的图象交于A点.
(1)求A点的坐标;
(2)观察图象:当1<x<3时,比较y1,y2的大小.
26.(本题7分)已知一次函数的图象经过点,且与正比例函数的图象相交于点.
求:(1)的值;
(2),的值;
(3)这两个函数图象与轴所围成的三角形的面积.
27.(本题7分)已知一次函数的图像经过点A(-1,-2),B(0,1).
(1)求k、b的值;
(2)画出这个函数的图像;
(3)当x>1时,y的取值范围是 .
28.(本题7分)小美打算在“母亲节”买一束百合和康乃馨组合的鲜花送给妈妈.已知买2支百合和1支康乃馨共需花费14元,3支康乃馨的价格比2支百合的价格多2元.
(1)求买一支康乃馨和一支百合各需多少元?
(2)小美准备买康乃馨和百合共11支,且康乃馨不多于9支,设买康乃馨x支,买这束鲜花所需总费用为w元.
①求w与x之间的函数关系式;
②请你帮小美设计一种使费用最少的买花方案,并求出最少费用.
29.(本题8分)商场出售一批进价为2元的贺年卡,在市场营销中发现此商品日销售单价x(元)与日销售量y(张)之间有如下关系:
x(元) 3 4 5 6
y(张) 16 14 12 10
(1)写出y关于x的函数关系式:____________;
(2)设经营此贺年卡的日销售利润为w(元),试求出w关于x的函数解析式;
(3)求出当日销售单价x定为多少元时,才能获得最大日销售利润,并求出最大日销售利润.
30.(本题8分)如图,直线与直线交于点.
(1)求m的值;
(2)方程组的解是________;
(3)直线是否也经过点P?请判断并说明理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:A、是一次函数,不是正比例函数,所以本选项不符合题意;
B、是二次函数,不是正比例函数,所以本选项不符合题意;
C、是正比例函数,所以本选项符合题意;
D、,不是正比例函数,所以本选项不符合题意.
2.B
【解析】由题意可知:,解得:m= 1故选B.
3.C
【解析】解:∵函数中,
则
∴;
故选:C.
4.B
【解析】解:∵直线经过一、二、四象限,
∴k<0,b>0,
∴点在第二象限,
故选B.
5.B
【解析】解:二元一次方程2x y=1的解可以为:
或.
所以,以方程2x y=1的解为坐标的点分别为:(,0)、(0,-1),
它们在平面直角坐标系中的图象如下图所示:
,
故选:B.
6.C
【解析】解:A、对于的每一个取值,可能有两个值与之对应,不符合题意;
B、对于的每一个取值,可能有两个值与之对应,不符合题意;
C、对于的每一个取值,都有唯一确定的值与之对应,符合题意;
D、对于的每一个取值,可能有两个值与之对应,不符合题意;
故选:
7.D
【解析】解:当点P在C→A路线上运动时,设点P运动速度为 ,
∴ ,
∵a、OA为常数,
∴S是关于t的一次函数,图象为自左向右上升的线段;
当A→B路线上运动时,
,保持不变,
∴本段图象为平行于x轴的线段;
当点P在B→O路线上运动时,
随着t的增大,点P从点B运动至点O,OM的长在减小,△OPM的高PM也随之减小到0,
即的图象为开口向下的抛物线的一部分.
故选:D
8.B
【解析】由题意得:
故选B
9.D
【解析】解:设售量y件与销售价x元之间的关系为y=kx+b,
将x=90,y=90与x=100,y=80分别代入可得:,
解得,
∴y=﹣x+180,
将x=137代入可得y=43,
故选:D.
10.A
【解析】A. 图像经过一、二、三象限,故该选项正确,符合题意;
B. 关于方程的解不一定是,不正确,不符合题意
C. 根据图象与轴的交点,可知,则,故该选项不正确,不符合题意;
D. 图象经过一、二、三象限,,随的增大而增大,故该选项不正确,不符合题意;
故选A
11.A
【解析】∵一次函数y=kx+b(k≠0)与x轴的交点坐标为(2,0),
∴y随x的增大而减小,
∴当x>2时,y<0.
故选:A.
12.D
【解析】解:直线和关于原点对称的直线为y=mx+3和,
∵直线和相交于点P(2,3),
∴直线y=mx+3和y=2xn相交于点(2,3),
∴方程组的解为;
故选:D.
13.2
【解析】解:∵已知自变量为x的函数y=mx+2-m是正比例函数,
∴m≠0,2﹣m=0,
∴m=2,
故答案为:2.
14.y
【解析】解:小轿车距银川的距离y(千米)与行驶时间x(时)的函数表达式为:y=130 80x,
故答案为:y=130 80x.
15.增大 (0,-3)
【解析】解:∵在函数y=4x-3中, 4>0,
∴y随x的增大而增大,
∵y轴上的点横坐标为0,当x=0时,y=-3.
∴函数图像与y轴的交点坐标是(0,-3).
故答案为:增大,(0,-3).
16.
【解析】解:根据题意,可设 ,
∵当时,,
∴ ,解得: ,
∴y与x之间的函数关系式为 .
故答案为:
17.
【解析】解:由图象可知,在点A左侧,直线的函数图像都在直线的函数图像得到下方,
即当时,.
∴不等式的解集为,
故答案为:.
18.6
【解析】∵,
∴
=2+4
=6.
故答案为:6.
19.①②④⑤
【解析】①是一次函数;②是一次函数,③不是一次函数,④是一次函数,⑤是一次函数.
故答案为:①②④⑤.
20.
【解析】解:观察图象知道,当x=0时,y=1,
∴当x≤0时,y≥1,
故答案为:x≤0.
21.1
【解析】解:当即时,是一次函数,符合题意;
当时,根据一次函数的定义可得:,
解得,
∴此时m无解,
综上所述,
故答案为:.
22.
【解析】解:根据题意,
∵一次函数的图象与x轴的交点为(2,0),
把向右平移1个单位,得,
∴与x轴的交点为(3,0),
∴关于的不等式的解集为;
故答案为:.
23.2
【解析】解:根据题意,可得|k-3|=1且k-3<0,
∴k-3=1或k-3=-1,
解得k1=4, k2=2,
∵k-3<0,
∴k<3,
∴k=2.
24.(1)m≠2;(2)m≠2且n=.
【解析】(1)由题意得,2-m≠0,解得m≠2.
(2)由题意得,2-m≠0且2n-3=0,解得m≠2且n=.
25.(1)A(2,-3)(2)当1<x<2时,y2>y1;当x=2时,y1=y2;当2<x<3时,y1>y2.
【解析】解:(1)联立两函数得,解得
∴A(2,-3)
(2)∵两函数交于A点,由图可得:
当1<x<2时,y2>y1;
当x=2时,y1=y2;
当2<x<3时,y1>y2.
26.(1);(2),;(3)2
【解析】解:(1)将代入得,.
(2)由(1)得,交点坐标为,
将,代入中,得,解得,
∴,.
(3)由(2)得,直线的表达式为,
令,则,所以直线与轴的交点坐标问为,
又∵两直线的交点坐标为,
∴.
27.(1);(2)见详解;(3)
【解析】解:(1)∵一次函数的图像经过点A(-1,-2),B(0,1)
∴,
∴;
(2)由(1)可知,一次函数为经过点A(-1,-2),B(0,1),如图:
(3)当时,则,
由图像可知,y随x增大而增大,
∴当x>1时,y的取值范围是;
故答案为:.
28.(1)买一支康乃馨需4元,买一支百合需5元;(2)①w=﹣x+55;②买9支康乃馨,买2支百合费用最少,最少费用为46元.
【解析】解:(1)设买一支康乃馨需m元,买一支百合需n元,
则根据题意得:,
解得: ,
答:买一支康乃馨需4元,买一支百合需5元;
(2)①根据题意得:w=4x+5(11﹣x)=﹣x+55,
②∵康乃馨不多于9支,
∴x≤9,
∵﹣1<0,
∴w随x的增大而减小,
∴当x=9时,w最小,
即买9支康乃馨,买11﹣9=2支百合费用最少,wmin=﹣9+55=46(元),
答:w与x之间的函数关系式:w=﹣x+55,买9支康乃馨,买2支百合费用最少,最少费用为46元.
29.(1);(2);(3)当日销售单价元时,才能获得最大日销售利润元.
【解析】解:(1)设,
将点代入,
,
解得:,
,
故答案是:;
(2)由题意得:
.
(3).
∴当时,w有最大值为.
答:(2)w关于x的函数解析式为.
(3)当日销售单价元时,才能获得最大日销售利润元.
30.(1)m=4;(2) ;(3)经过,理由见解析
【解析】(1)将点代入直线,得,解得.
(2)由(1)可知点坐标为(-1,4),依题意得:
解得:
∴直线的解析式为
联立两个直线解析式得:
解得:.
故答案为.
(3)直线也经过点P.理由如下
点P的坐标为,在直线上,
.
将代人直线中,得,
直线也经过点.
答案第1页,共2页
答案第1页,共2页
第六章 一次函数 单元过关检测
时间:120分钟满分:120分
一、单选题(共36分)
1.(本题3分)下列各函数中,是正比例函数的是( )
A. B.
C. D.
2.(本题3分)已知函数是一次函数,则的值为( )
A.1 B. C.0或 D.1或
3.(本题3分)在函数中,自变量的取值范围是( )
A. B. C. D.
4.(本题3分)如图是函数的图像,则点在( )象限内
A.第一 B.第二 C.第三 D.第四
5.(本题3分)以二元一次方程的解为坐标的点组成的图象画在坐标系中可能是( )
A. B.
C. D.
6.(本题3分)下列曲线中,表示y是x的函数的是( )
A. B. C. D.
7.(本题3分)如图,已知点A、B在反比例函数y(k>0,x>0)的图象上,点P沿C→A→B→O的路线(图中“→”所示路线)匀速运动,过点P作PM⊥x轴于点M,设点P的运动时间为t,△POM的面积为S,则S关于t的函数图象大致为( )
A. B.
C. D.
8.(本题3分)某商场为了增加销售额,推出“七月销售大酬宾”活动,其活动内容为:“凡七月份在该商场一次性购物超过100元以上者,超过100元的部分按9折优惠”.在大酬宾活动中,小王到该商场为单位购买单价为60元的办公用品x件(),则应付货款y(元)与商品件数x的函数关系式是( )
A. B.
C. D.
9.(本题3分)在某一阶段,某商品的销售量与销售价之间存在如下关系:设该商品的销售价为x元,售量为y件,估计当x=137时,y的值可能为( )
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
A.63 B.59 C.53 D.43
10.(本题3分)如图,一次函数的图象经过点,则下列结论正确的是( )
A.图像经过一、二、三象限 B.关于方程的解是
C. D.随的增大而减小
11.(本题3分)一次函数y=kx+b(k≠0)的图象如图所示,当x>2时,y的取值范围是( )
A.y<0 B.y>0 C.y<3 D.y>3
12.(本题3分)若直线和相交于点,则方程组的解为( )
A. B. C. D.
二、填空题(共30分)
13.(本题3分)已知自变量为x的函数y=mx+2-m是正比例函数,则m=_________ .
14.(本题3分)从中宁到银川的距离为130千米,一辆小轿车车以平均每小时80千米的速度从中宁出发到银川,则小轿车距银川的距离y(千米)与行驶时间x(时)的函数表达式为______.
15.(本题3分)函数中,的值随着值的增大而______,它的图象与轴的交点坐标是______.
16.(本题3分)已知y与成正比例,且当时,,则y与x之间的函数关系式为______________.
17.(本题3分)如图,函数和的图象相交于,则不等式的解集为____.
18.(本题3分)函数,则当函数自变量时,y=______
19.(本题3分)下列函数:①,②,③,④,⑤其中是一次函数的有_____.(填序号)
20.(本题3分)一次函数y=kx+b的图象如图所示,当x满足 _____时,y≥1.
21.(本题3分)已知函数y=(m﹣1)+2x+1为一次函数,则m=____.
22.(本题3分)一次函数的图象如图所示,则关于的不等式的解集为______.
三、解答题(共54分)
23.(本题5分)在正比例函数y=(k-3)x|k-3|中,函数值y随x的增大而减小,求k的值.
24.(本题6分)已知函数y=(2-m)x+2n-3.求当m为何值时.
(1)此函数为一次函数
(2)此函数为正比例函数
25.(本题6分)如图,已知两个一次函数y1=x﹣6和y2=﹣x的图象交于A点.
(1)求A点的坐标;
(2)观察图象:当1<x<3时,比较y1,y2的大小.
26.(本题7分)已知一次函数的图象经过点,且与正比例函数的图象相交于点.
求:(1)的值;
(2),的值;
(3)这两个函数图象与轴所围成的三角形的面积.
27.(本题7分)已知一次函数的图像经过点A(-1,-2),B(0,1).
(1)求k、b的值;
(2)画出这个函数的图像;
(3)当x>1时,y的取值范围是 .
28.(本题7分)小美打算在“母亲节”买一束百合和康乃馨组合的鲜花送给妈妈.已知买2支百合和1支康乃馨共需花费14元,3支康乃馨的价格比2支百合的价格多2元.
(1)求买一支康乃馨和一支百合各需多少元?
(2)小美准备买康乃馨和百合共11支,且康乃馨不多于9支,设买康乃馨x支,买这束鲜花所需总费用为w元.
①求w与x之间的函数关系式;
②请你帮小美设计一种使费用最少的买花方案,并求出最少费用.
29.(本题8分)商场出售一批进价为2元的贺年卡,在市场营销中发现此商品日销售单价x(元)与日销售量y(张)之间有如下关系:
x(元) 3 4 5 6
y(张) 16 14 12 10
(1)写出y关于x的函数关系式:____________;
(2)设经营此贺年卡的日销售利润为w(元),试求出w关于x的函数解析式;
(3)求出当日销售单价x定为多少元时,才能获得最大日销售利润,并求出最大日销售利润.
30.(本题8分)如图,直线与直线交于点.
(1)求m的值;
(2)方程组的解是________;
(3)直线是否也经过点P?请判断并说明理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:A、是一次函数,不是正比例函数,所以本选项不符合题意;
B、是二次函数,不是正比例函数,所以本选项不符合题意;
C、是正比例函数,所以本选项符合题意;
D、,不是正比例函数,所以本选项不符合题意.
2.B
【解析】由题意可知:,解得:m= 1故选B.
3.C
【解析】解:∵函数中,
则
∴;
故选:C.
4.B
【解析】解:∵直线经过一、二、四象限,
∴k<0,b>0,
∴点在第二象限,
故选B.
5.B
【解析】解:二元一次方程2x y=1的解可以为:
或.
所以,以方程2x y=1的解为坐标的点分别为:(,0)、(0,-1),
它们在平面直角坐标系中的图象如下图所示:
,
故选:B.
6.C
【解析】解:A、对于的每一个取值,可能有两个值与之对应,不符合题意;
B、对于的每一个取值,可能有两个值与之对应,不符合题意;
C、对于的每一个取值,都有唯一确定的值与之对应,符合题意;
D、对于的每一个取值,可能有两个值与之对应,不符合题意;
故选:
7.D
【解析】解:当点P在C→A路线上运动时,设点P运动速度为 ,
∴ ,
∵a、OA为常数,
∴S是关于t的一次函数,图象为自左向右上升的线段;
当A→B路线上运动时,
,保持不变,
∴本段图象为平行于x轴的线段;
当点P在B→O路线上运动时,
随着t的增大,点P从点B运动至点O,OM的长在减小,△OPM的高PM也随之减小到0,
即的图象为开口向下的抛物线的一部分.
故选:D
8.B
【解析】由题意得:
故选B
9.D
【解析】解:设售量y件与销售价x元之间的关系为y=kx+b,
将x=90,y=90与x=100,y=80分别代入可得:,
解得,
∴y=﹣x+180,
将x=137代入可得y=43,
故选:D.
10.A
【解析】A. 图像经过一、二、三象限,故该选项正确,符合题意;
B. 关于方程的解不一定是,不正确,不符合题意
C. 根据图象与轴的交点,可知,则,故该选项不正确,不符合题意;
D. 图象经过一、二、三象限,,随的增大而增大,故该选项不正确,不符合题意;
故选A
11.A
【解析】∵一次函数y=kx+b(k≠0)与x轴的交点坐标为(2,0),
∴y随x的增大而减小,
∴当x>2时,y<0.
故选:A.
12.D
【解析】解:直线和关于原点对称的直线为y=mx+3和,
∵直线和相交于点P(2,3),
∴直线y=mx+3和y=2xn相交于点(2,3),
∴方程组的解为;
故选:D.
13.2
【解析】解:∵已知自变量为x的函数y=mx+2-m是正比例函数,
∴m≠0,2﹣m=0,
∴m=2,
故答案为:2.
14.y
【解析】解:小轿车距银川的距离y(千米)与行驶时间x(时)的函数表达式为:y=130 80x,
故答案为:y=130 80x.
15.增大 (0,-3)
【解析】解:∵在函数y=4x-3中, 4>0,
∴y随x的增大而增大,
∵y轴上的点横坐标为0,当x=0时,y=-3.
∴函数图像与y轴的交点坐标是(0,-3).
故答案为:增大,(0,-3).
16.
【解析】解:根据题意,可设 ,
∵当时,,
∴ ,解得: ,
∴y与x之间的函数关系式为 .
故答案为:
17.
【解析】解:由图象可知,在点A左侧,直线的函数图像都在直线的函数图像得到下方,
即当时,.
∴不等式的解集为,
故答案为:.
18.6
【解析】∵,
∴
=2+4
=6.
故答案为:6.
19.①②④⑤
【解析】①是一次函数;②是一次函数,③不是一次函数,④是一次函数,⑤是一次函数.
故答案为:①②④⑤.
20.
【解析】解:观察图象知道,当x=0时,y=1,
∴当x≤0时,y≥1,
故答案为:x≤0.
21.1
【解析】解:当即时,是一次函数,符合题意;
当时,根据一次函数的定义可得:,
解得,
∴此时m无解,
综上所述,
故答案为:.
22.
【解析】解:根据题意,
∵一次函数的图象与x轴的交点为(2,0),
把向右平移1个单位,得,
∴与x轴的交点为(3,0),
∴关于的不等式的解集为;
故答案为:.
23.2
【解析】解:根据题意,可得|k-3|=1且k-3<0,
∴k-3=1或k-3=-1,
解得k1=4, k2=2,
∵k-3<0,
∴k<3,
∴k=2.
24.(1)m≠2;(2)m≠2且n=.
【解析】(1)由题意得,2-m≠0,解得m≠2.
(2)由题意得,2-m≠0且2n-3=0,解得m≠2且n=.
25.(1)A(2,-3)(2)当1<x<2时,y2>y1;当x=2时,y1=y2;当2<x<3时,y1>y2.
【解析】解:(1)联立两函数得,解得
∴A(2,-3)
(2)∵两函数交于A点,由图可得:
当1<x<2时,y2>y1;
当x=2时,y1=y2;
当2<x<3时,y1>y2.
26.(1);(2),;(3)2
【解析】解:(1)将代入得,.
(2)由(1)得,交点坐标为,
将,代入中,得,解得,
∴,.
(3)由(2)得,直线的表达式为,
令,则,所以直线与轴的交点坐标问为,
又∵两直线的交点坐标为,
∴.
27.(1);(2)见详解;(3)
【解析】解:(1)∵一次函数的图像经过点A(-1,-2),B(0,1)
∴,
∴;
(2)由(1)可知,一次函数为经过点A(-1,-2),B(0,1),如图:
(3)当时,则,
由图像可知,y随x增大而增大,
∴当x>1时,y的取值范围是;
故答案为:.
28.(1)买一支康乃馨需4元,买一支百合需5元;(2)①w=﹣x+55;②买9支康乃馨,买2支百合费用最少,最少费用为46元.
【解析】解:(1)设买一支康乃馨需m元,买一支百合需n元,
则根据题意得:,
解得: ,
答:买一支康乃馨需4元,买一支百合需5元;
(2)①根据题意得:w=4x+5(11﹣x)=﹣x+55,
②∵康乃馨不多于9支,
∴x≤9,
∵﹣1<0,
∴w随x的增大而减小,
∴当x=9时,w最小,
即买9支康乃馨,买11﹣9=2支百合费用最少,wmin=﹣9+55=46(元),
答:w与x之间的函数关系式:w=﹣x+55,买9支康乃馨,买2支百合费用最少,最少费用为46元.
29.(1);(2);(3)当日销售单价元时,才能获得最大日销售利润元.
【解析】解:(1)设,
将点代入,
,
解得:,
,
故答案是:;
(2)由题意得:
.
(3).
∴当时,w有最大值为.
答:(2)w关于x的函数解析式为.
(3)当日销售单价元时,才能获得最大日销售利润元.
30.(1)m=4;(2) ;(3)经过,理由见解析
【解析】(1)将点代入直线,得,解得.
(2)由(1)可知点坐标为(-1,4),依题意得:
解得:
∴直线的解析式为
联立两个直线解析式得:
解得:.
故答案为.
(3)直线也经过点P.理由如下
点P的坐标为,在直线上,
.
将代人直线中,得,
直线也经过点.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
