安徽省滁州市全椒县2021-2022学年九年级上学期期末统考数学试卷(word版含图片答案)
文档属性
| 名称 | 安徽省滁州市全椒县2021-2022学年九年级上学期期末统考数学试卷(word版含图片答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 20:41:55 | ||
图片预览

文档简介
安徽滁州市全椒县2021-2022学年九上期末(统考)数学试卷(含答案)
温馨提示:本试卷内容沪科版九上全册第21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1、抛物线y=3(x-1)+8的顶点坐标为( )
A. (1,8) B.(-1,8) C. (-1,-8) D. (1,-8)
2、反比例函数y=经过点(2,1),则下列说法错误的是( )
A. k=2 B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大 D.当x>0时,y随x的增大而减小
3、如图,点P在ΔABC的边AC上,下列条件中不能判定△ABP∽△ACB的是( )
A.∠ABP=∠C B.∠APB=∠ABC C AP:AB=AB:AC D AB:BP=AC:CB
第3题图 第4题图 第5题图
4、如图,已知A为反比例函数y=(x<0)图象上一点,过点A作AB⊥y轴,垂足为B,若Δ0AB面积为2,则k的值为( )
A.2 B.-2 C.4 D.-4
5、如图,树AB在路灯0的照射下形成影子AC,已知路灯高P0=5m,树影AC=3m,树AB与路灯0的水平距离AP=
4.5m,点C、A、P在同一水平线上,则树的高度AB长是( )
A.3m B.2m C m D. m
6、如图,已知AB和CD是⊙0的两条等弦,OM⊥AB、ON⊥CD,垂足分别为M、N,BA、DC的延长线交于点P,连接OP.下列四个说法:①AB=CD;②0M=ON;③PA=PC;④∠BPO=∠DPO;正确的个数是( )
A.1 B.2 C.3 D.4
第6题图 第7题图 第8题图 第9题图
7、如图,在△ABC中,点D、E、F"分别在边AB、AC、BC上,且DE//BC、EF//AB,若AD=2BD,则CF:BF的值为
( )
A B C D
8、如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.4tanα米 B.4sinα米 C.4cosα米 D 米
9、如图,矩形纸片ABCD,AD:AB=:1,点E、F分别在AD、BC上,把纸片如图沿EF折叠,点A、B的对应点
分别为A'、B',连接AA'并延长交线段CD于点G,则EF:AG的值为( )
A B C D
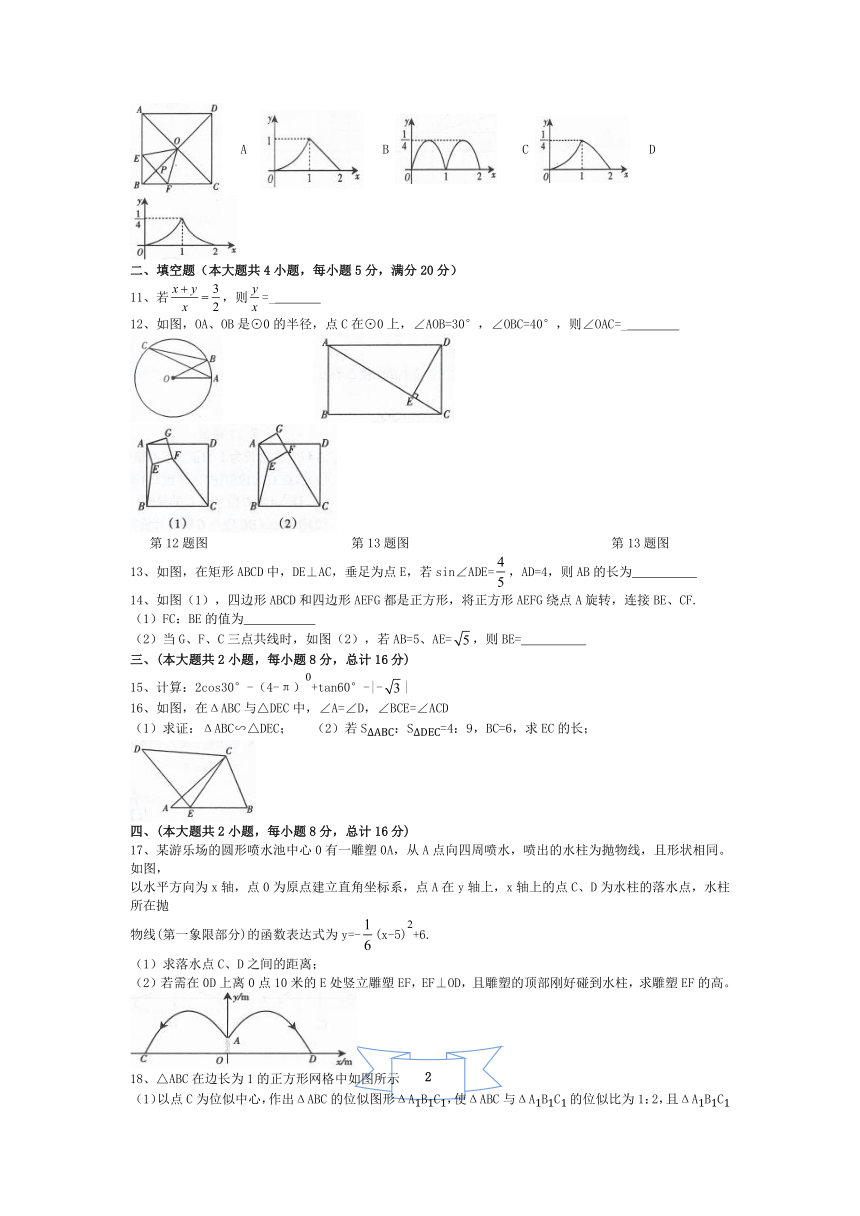
10、在边长为的正方形ABCD中,对角线AC与BD相交于点0,P是BD上一动点,过P作EF//AC,分别交正方形的两条边于点E、F,设BP=x,ΔOEF的面积为y,则能反映y与x之间关系的图象为( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、若,则=_
12、如图,OA、OB是⊙0的半径,点C在⊙0上,∠AOB=30°,∠OBC=40°,则∠OAC=_
第12题图 第13题图 第13题图
13、如图,在矩形ABCD中,DE⊥AC,垂足为点E,若sin∠ADE=,AD=4,则AB的长为
14、如图(1),四边形ABCD和四边形AEFG都是正方形,将正方形AEFG绕点A旋转,连接BE、CF.
(1)FC:BE的值为
(2)当G、F、C三点共线时,如图(2),若AB=5、AE=,则BE=
三、(本大题共2小题,每小题8分,总计16分)
15、计算:2cos30°-(4-π)+tan60°-|-|
16、如图,在ΔABC与△DEC中,∠A=∠D,∠BCE=∠ACD
(1)求证:ΔABC∽△DEC; (2)若SΔABC:SΔDEC=4:9,BC=6,求EC的长;
四、(本大题共2小题,每小题8分,总计16分)
17、某游乐场的圆形喷水池中心0有一雕塑0A,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,
以水平方向为x轴,点0为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛
物线(第一象限部分)的函数表达式为y=-(x-5)+6.
(1)求落水点C、D之间的距离;
(2)若需在0D上离0点10米的E处竖立雕塑EF,EF⊥OD,且雕塑的顶部刚好碰到水柱,求雕塑EF的高。
18、△ABC在边长为1的正方形网格中如图所示
(1)以点C为位似中心,作出ΔABC的位似图形ΔA1B1C1,使ΔABC与ΔA1B1C1的位似比为1:2,且ΔA1B1C1位于点C的异侧;
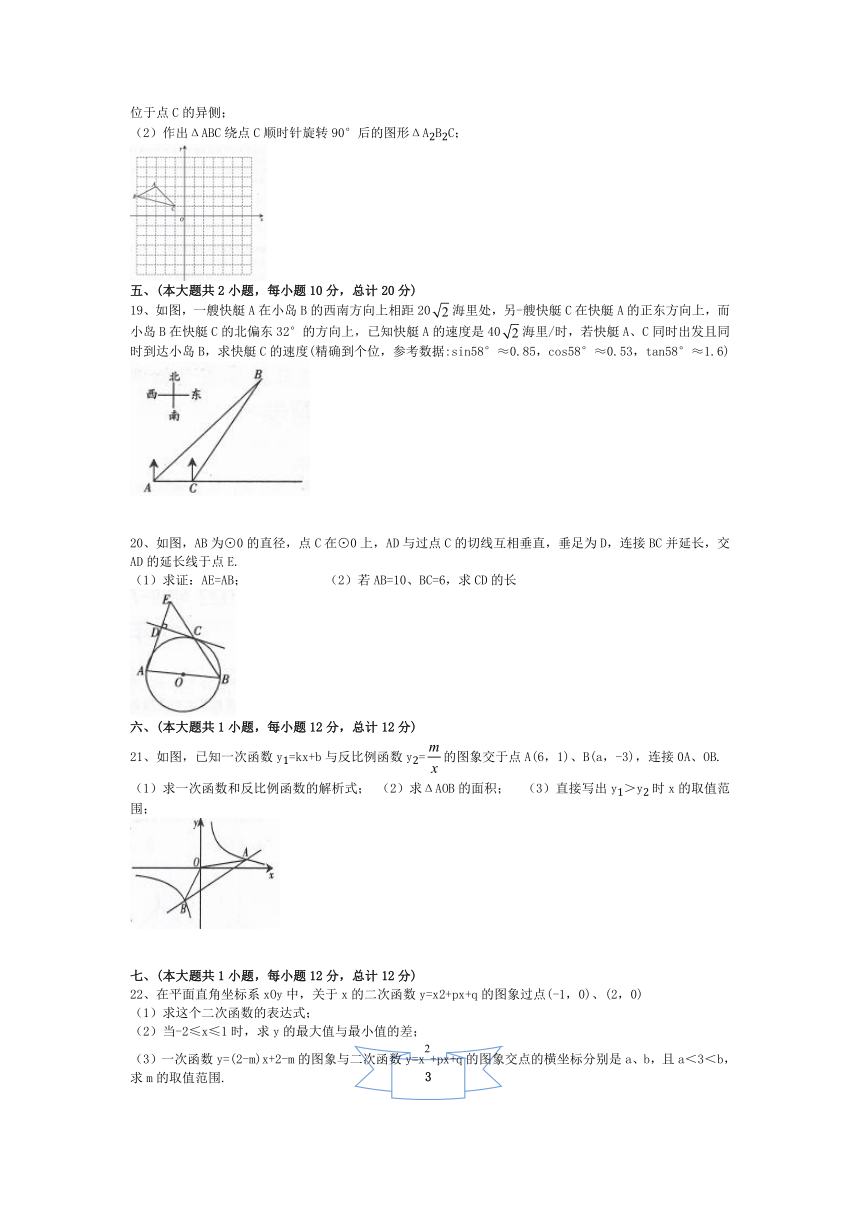
(2)作出ΔABC绕点C顺时针旋转90°后的图形ΔA2B2C;
五、(本大题共2小题,每小题10分,总计20分)
19、如图,一艘快艇A在小岛B的西南方向上相距20海里处,另-艘快艇C在快艇A的正东方向上,而小岛B在快艇C的北偏东32°的方向上,已知快艇A的速度是40海里/时,若快艇A、C同时出发且同时到达小岛B,求快艇C的速度(精确到个位,参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)
20、如图,AB为⊙0的直径,点C在⊙0上,AD与过点C的切线互相垂直,垂足为D,连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB; (2)若AB=10、BC=6,求CD的长
六、(本大题共1小题,每小题12分,总计12分)
21、如图,已知一次函数y1=kx+b与反比例函数y2=的图象交于点A(6,1)、B(a,-3),连接0A、OB.
(1)求一次函数和反比例函数的解析式; (2)求ΔAOB的面积; (3)直接写出y1>y2时x的取值范围;
七、(本大题共1小题,每小题12分,总计12分)
22、在平面直角坐标系xOy中,关于x的二次函数y=x2+px+q的图象过点(-1,0)、(2,0)
(1)求这个二次函数的表达式;
(2)当-2≤x≤1时,求y的最大值与最小值的差;
(3)一次函数y=(2-m)x+2-m的图象与二次函数y=x+px+q的图象交点的横坐标分别是a、b,且a<3<b,求m的取值范围.
八、(本大题共1小题,每小题14分,总计14分)
23、如图,E是矩形ABCD边AB的中点,F是BC边上一点,线段DE和AF相交于点P,连接PC,过点A作AQ//PC交PD于点Q.
(1)求证:PC=2AQ;
(2)已知AD=PD DE,AB=10,AD=12,求BF的长;
(3)当F是BC的中点时,求AP:PF的长;
安徽滁州市全椒县2021-2022学年九上期末(统考)数学试卷答案
(
1
)
温馨提示:本试卷内容沪科版九上全册第21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1、抛物线y=3(x-1)+8的顶点坐标为( )
A. (1,8) B.(-1,8) C. (-1,-8) D. (1,-8)
2、反比例函数y=经过点(2,1),则下列说法错误的是( )
A. k=2 B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大 D.当x>0时,y随x的增大而减小
3、如图,点P在ΔABC的边AC上,下列条件中不能判定△ABP∽△ACB的是( )
A.∠ABP=∠C B.∠APB=∠ABC C AP:AB=AB:AC D AB:BP=AC:CB
第3题图 第4题图 第5题图
4、如图,已知A为反比例函数y=(x<0)图象上一点,过点A作AB⊥y轴,垂足为B,若Δ0AB面积为2,则k的值为( )
A.2 B.-2 C.4 D.-4
5、如图,树AB在路灯0的照射下形成影子AC,已知路灯高P0=5m,树影AC=3m,树AB与路灯0的水平距离AP=
4.5m,点C、A、P在同一水平线上,则树的高度AB长是( )
A.3m B.2m C m D. m
6、如图,已知AB和CD是⊙0的两条等弦,OM⊥AB、ON⊥CD,垂足分别为M、N,BA、DC的延长线交于点P,连接OP.下列四个说法:①AB=CD;②0M=ON;③PA=PC;④∠BPO=∠DPO;正确的个数是( )
A.1 B.2 C.3 D.4
第6题图 第7题图 第8题图 第9题图
7、如图,在△ABC中,点D、E、F"分别在边AB、AC、BC上,且DE//BC、EF//AB,若AD=2BD,则CF:BF的值为
( )
A B C D
8、如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.4tanα米 B.4sinα米 C.4cosα米 D 米
9、如图,矩形纸片ABCD,AD:AB=:1,点E、F分别在AD、BC上,把纸片如图沿EF折叠,点A、B的对应点
分别为A'、B',连接AA'并延长交线段CD于点G,则EF:AG的值为( )
A B C D
10、在边长为的正方形ABCD中,对角线AC与BD相交于点0,P是BD上一动点,过P作EF//AC,分别交正方形的两条边于点E、F,设BP=x,ΔOEF的面积为y,则能反映y与x之间关系的图象为( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、若,则=_
12、如图,OA、OB是⊙0的半径,点C在⊙0上,∠AOB=30°,∠OBC=40°,则∠OAC=_
第12题图 第13题图 第13题图
13、如图,在矩形ABCD中,DE⊥AC,垂足为点E,若sin∠ADE=,AD=4,则AB的长为
14、如图(1),四边形ABCD和四边形AEFG都是正方形,将正方形AEFG绕点A旋转,连接BE、CF.
(1)FC:BE的值为
(2)当G、F、C三点共线时,如图(2),若AB=5、AE=,则BE=
三、(本大题共2小题,每小题8分,总计16分)
15、计算:2cos30°-(4-π)+tan60°-|-|
16、如图,在ΔABC与△DEC中,∠A=∠D,∠BCE=∠ACD
(1)求证:ΔABC∽△DEC; (2)若SΔABC:SΔDEC=4:9,BC=6,求EC的长;
四、(本大题共2小题,每小题8分,总计16分)
17、某游乐场的圆形喷水池中心0有一雕塑0A,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,
以水平方向为x轴,点0为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛
物线(第一象限部分)的函数表达式为y=-(x-5)+6.
(1)求落水点C、D之间的距离;
(2)若需在0D上离0点10米的E处竖立雕塑EF,EF⊥OD,且雕塑的顶部刚好碰到水柱,求雕塑EF的高。
18、△ABC在边长为1的正方形网格中如图所示
(1)以点C为位似中心,作出ΔABC的位似图形ΔA1B1C1,使ΔABC与ΔA1B1C1的位似比为1:2,且ΔA1B1C1位于点C的异侧;
(2)作出ΔABC绕点C顺时针旋转90°后的图形ΔA2B2C;
五、(本大题共2小题,每小题10分,总计20分)
19、如图,一艘快艇A在小岛B的西南方向上相距20海里处,另-艘快艇C在快艇A的正东方向上,而小岛B在快艇C的北偏东32°的方向上,已知快艇A的速度是40海里/时,若快艇A、C同时出发且同时到达小岛B,求快艇C的速度(精确到个位,参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)
20、如图,AB为⊙0的直径,点C在⊙0上,AD与过点C的切线互相垂直,垂足为D,连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB; (2)若AB=10、BC=6,求CD的长
六、(本大题共1小题,每小题12分,总计12分)
21、如图,已知一次函数y1=kx+b与反比例函数y2=的图象交于点A(6,1)、B(a,-3),连接0A、OB.
(1)求一次函数和反比例函数的解析式; (2)求ΔAOB的面积; (3)直接写出y1>y2时x的取值范围;
七、(本大题共1小题,每小题12分,总计12分)
22、在平面直角坐标系xOy中,关于x的二次函数y=x2+px+q的图象过点(-1,0)、(2,0)
(1)求这个二次函数的表达式;
(2)当-2≤x≤1时,求y的最大值与最小值的差;
(3)一次函数y=(2-m)x+2-m的图象与二次函数y=x+px+q的图象交点的横坐标分别是a、b,且a<3<b,求m的取值范围.
八、(本大题共1小题,每小题14分,总计14分)
23、如图,E是矩形ABCD边AB的中点,F是BC边上一点,线段DE和AF相交于点P,连接PC,过点A作AQ//PC交PD于点Q.
(1)求证:PC=2AQ;
(2)已知AD=PD DE,AB=10,AD=12,求BF的长;
(3)当F是BC的中点时,求AP:PF的长;
安徽滁州市全椒县2021-2022学年九上期末(统考)数学试卷答案
(
1
)
同课章节目录
