人教A版(2019)必修第一册必杀技第二章2.2基本不等式(Word含答案解析)
文档属性
| 名称 | 人教A版(2019)必修第一册必杀技第二章2.2基本不等式(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 19:33:15 | ||
图片预览




文档简介
人教A版(2019)必修第一册必杀技第二章2.2基本不等式
一、单选题
1.下列各函数中,最小值为4的是( )
A. B.
C. D.
2.设,,则的最小值为( )
A. B. C. D.
3.已知,,,则的最小值是( ).
A.3 B. C. D.9
4.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明,现有如图所示图形,点在半圆上,点在直径上,且,设,,则该图形可以完成的无字证明为( )
A. B.
C. D.
5.已知抛物线的焦点为,为坐标原点,设为抛物线上的动点,则的最大值为
A. B. C. D.
6.双曲线的离心率是,则的最小值为
A. B. C. D.
7.若,则下列不等式成立的是( ).A. B.
C. D.
8.下列不等式中,正确的是( )
A.a+≥4 B.a2+b2≥4ab
C.≥ D.x2+≥2
9.若函数,的图象都是一条连续不断的曲线,定义:.若函数和的定义域是,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.若,则当取得最大值时,x的值为( )
A.1 B. C. D.
11.已知,,,则的最小值为( )
A. B.1 C.2 D.4
12.若直线(,)平分圆的周长,则的最小值为
A. B. C. D.
13.在平面直角坐标系中,圆被直线()截得的弦长为,角的始边是轴的非负半轴,终边过点,则的最小值
A. B.1 C. D.2
14.小明同学计划两次购买同种笔芯(两次笔芯的单价不同),有两种方案:第一种方法是每次购买笔芯数量一定;第二种方法是每次购买笔芯所花钱数一定.则哪种购买方式比较经济( )
A.第一种 B.第二种
C.两种一样 D.无法判断
15.已知P=a2+(a≠0),Q=b2-4b+7(1<b≤3).则P、Q的大小关系为( )
A.P>Q B.P<Q C.P≥Q D.P≤Q
16.已知在中,角,,所对的边分别为,,,且,点为其外接圆的圆心.已知,则当角取到最大值时的面积为
A. B. C. D.
17.若,且,则下列结论一定正确的是( )
①②③④
A.①② B.②③ C.①③ D.①④
18.已知,则的最小值是( )
A.1 B.4 C.7 D.
19.设为坐标原点,是以为焦点的抛物线上任意一点,是线段上的点,且,则直线的斜率的最大值为
A. B. C. D.1
20.已知正数组成的等比数列的前8项的积是81,那么的最小值是( )
A. B. C.8 D.6
21.已知均为正实数,函数的图象过点,则的最小值为
A.2 B.3 C.4 D.5
22.已知,,,则的最大值为( )
A. B. C.1 D.
23.若,则的最小值为( )
A. B. C. D.
24.若且,则,,,中的最大值的是( )
A. B. C. D.
25.下列不等式中正确的是( )
A. B. C. D.
二、多选题
26.若,且,则( )
A. B.
C. D.
三、填空题
27.已知,且,则xy的最大值为___________
28.若、是实数,且,则取值范围是______.
29.若正实数满足,则的最小值为_____.
30.已知全集U=R,实数a,b满足a>b>0,集合M={x|<x<a},N={x|b},则_________
31.已知正数满足,则的最小值为________.
32.已知不等式对任意正实数,恒成立,则正实数的最小值为______.
33.已知正数x,y满足,则的最小值为________
34.已知,,且,若恒成立,则实数t的取值范围是________.
35.已知满足约束条件,且的最大值为1,则的最小值为________.
36.若,则的最小值为 __________.
37.如图,在△ABC中,E为边AC上一点,且,P为BE上一点,且满足,则的最小值为______.
38.已知,,,则的最小值是______.
39.定义:设函数在上的导函数为,若在上也存在导函数,则称函数在上存在二阶导函数,简记为.若在区间上,则称函数在区间上为“凸函数”.已知在区间上为“凸函数”,则实数的取值范围为______.
40.若,则的最小值为__.
41.已知一次函数图象与轴、轴分别交于点、,点在线段上,轴于点,轴于点,则矩形面积的最大值是_____________ ;
四、解答题
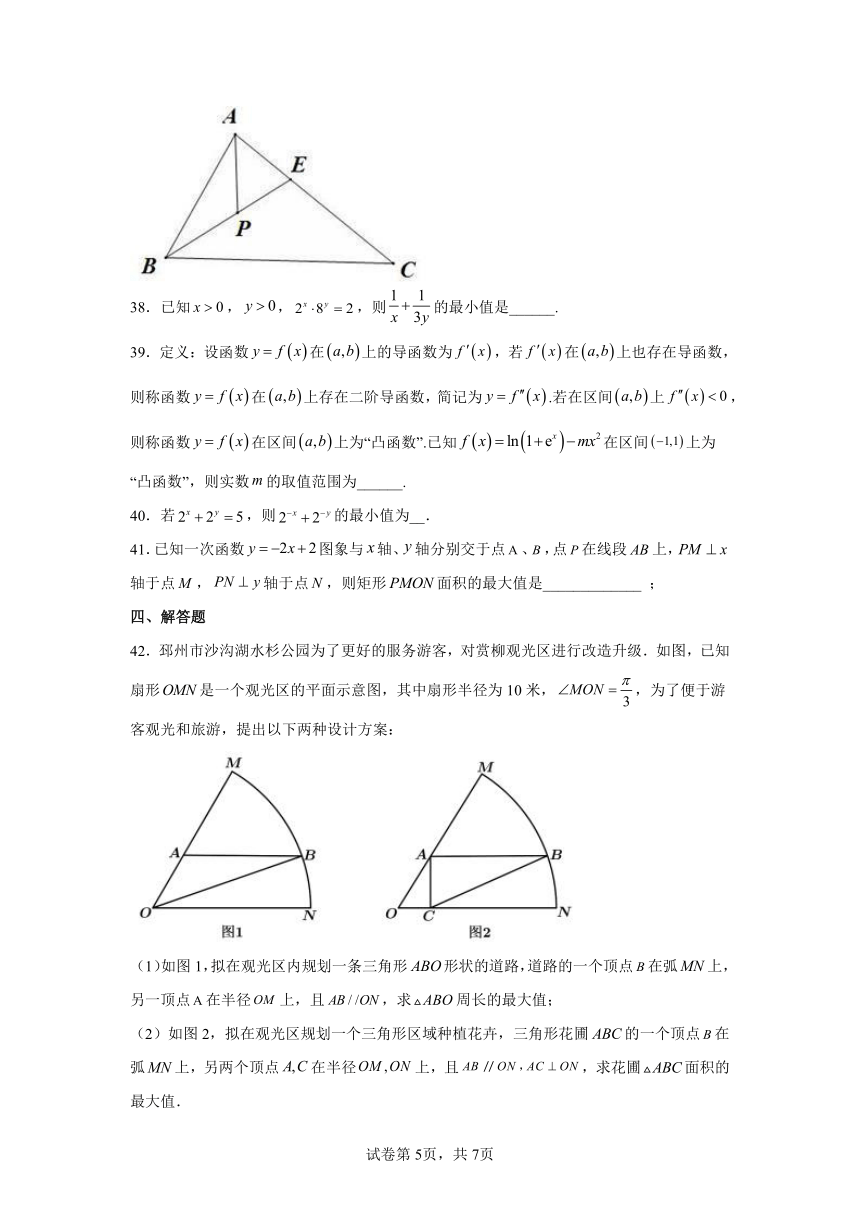
42.邳州市沙沟湖水杉公园为了更好的服务游客,对赏柳观光区进行改造升级.如图,已知扇形是一个观光区的平面示意图,其中扇形半径为10米,,为了便于游客观光和旅游,提出以下两种设计方案:
(1)如图1,拟在观光区内规划一条三角形形状的道路,道路的一个顶点在弧上,另一顶点在半径上,且,求周长的最大值;
(2)如图2,拟在观光区规划一个三角形区域种植花卉,三角形花圃的一个顶点在弧上,另两个顶点在半径上,且,求花圃面积的最大值.
43.已知.
(1)若方程有两个不等实根,求实数的范围;
(2)当,时,求的取值范围.
44.已知x+y=1,x,y∈R+.
(1)求x2+y2+xy的最小值;
(2)求的最大值;
(3)求x(1-3y)的最小值.
45.选修4-4:坐标系与参数方程
某县一中计划把一块边长为米的等边的边角地开辟为植物新品种实验基地,图4中需要把基地分成面积相等的两部分,在上,在上.
(1)设,使用表示的函数关系式;
(2)如果是灌溉输水管道的位置,为了节约,的位置应该在哪里?求出最小值.
46.证明下列不等式
(1)若bc-ad≥0,bd>0,求证:
(2)已知a>0,b>0,求证:
47.已知为正实数,且满足.
(1)若恒成立,求的最小值;
(2)证明:.
48.如图1,一个铝合金窗是由一个框架和部分外推窗框组成,其中框架设计如图2,其结构为上、下两栏,下栏为两个完全相同的矩形,四周框架和中间隔栏的材料为铝合金,宽均为,上栏和下栏的框内矩形高度(不含铝合金部分)比为,此铝合金窗占用的墙面面积为,设该铝合金窗的宽和高分别,,铝合金的透光部分的面积为(外推窗框遮挡光线部分忽略不计).
(1)试用,表示;
(2)若要使最大,则铝合金窗的宽和高分别为多少?
49.为迎接2018年省运会,宁德市某体育馆需要重新铺设塑胶跑道.已知每毫米厚的跑道的铺设成本为10万元,跑道平均每年的维护费C(单位:万元)与跑道厚度x(单位:毫米)的关系为C(x)=,x∈[10,15].若跑道厚度为10毫米,则平均每年的维护费需要9万元.设总费用f(x)为跑道铺设费用与10年维护费之和.
(1)求k的值与总费用f(x)的表达式;
(2)塑胶跑道铺设多厚时,总费用f(x)最小,并求最小值.
试卷第页,共页
试卷第页,共页
参考答案:
1.D
【解析】
【分析】
直接利用基本不等式.和关系式的恒等变换的应用求出结果.
【详解】
解:用基本不等式要满足“一正二定三相等“.
.选项中的正负不确定.同样的,
,选项中和取值不一定大于0.
.当时,,,,
时不符合,所以也不能用基本不等式,不满足三相等,
.,且,
当且仅当即时取等号.
故选:.
【点睛】
本题考查的知识要点:直接利用基本不等式的性质的应用和用基本不等式要满足“一正二定三相等“.的条件的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
2.B
【解析】
利用,,,且;
对进行分类讨论,分为和,进行讨论,
然后,求解即可得到的最小值
【详解】
,,,且;
当,;当且仅当
,又,解得或,又由,得时,此时,,的最小值;
当,,当且仅当时,解得或,又由,得,此时,,的最小值;
综上,的最小值;
故选:B
【点睛】
关键点睛:解题的关键在于利用,,,可得且,对进行分类讨论,难点在于利用基本不等式进行求最值,本题属于中档题
3.B
【解析】
【分析】
由已知结合指数与对数的运算性质可得,从而,展开后利用基本不等式可得解.
【详解】
,,,
所以,即,
所以,
则,
当且仅当且即,时取等号,
则的最小值是.
故选.
【点睛】
本题主要考查了指数与对数的运算性质及利用基本不等式求解最值,要注意应用条件的配凑.
4.B
【解析】
【分析】
由图形可知:,在直角中,利用勾股定理求得,结合,即可求解.
【详解】
由图形可知:,
在直角中,利用勾股定理,可得,
因为,所以.
故选:B.
5.D
【解析】
【分析】
由抛物线方程为:y2=2px(p>0),可得:焦点F(,0),由抛物线的定义可得,化简再换元,利用基本不等式求得最大值.
【详解】
由抛物线方程为:y2=2px(p>0),可得:
焦点F(,0),
设M(m,n),则n2=2pm,m>0,设M 到准线x的距离等于d,
则.
令 pmt,t,则 m,
∴(当且仅当 t 时,等号成立).
故的最大值为,
故选D.
【点睛】
本题考查抛物线的定义、基本不等式的应用,考查换元的思想,解题的关键是表达出,再利用基本不等式,综合性强.
6.C
【解析】
【详解】
,则,当即时取最小值,故选C.
【易错点晴】本题主要考查双曲线的离心率及利用基本不等式求最值,属于难题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).
7.B
【解析】
直接根据基本不等式判断即可.
【详解】
因为,
所以,当且仅当时等号成立,
由,
所以,
故选:B
8.D
【解析】
【分析】
举例说明ABC错误,利用基本不等式证明D成立.
【详解】
a<0,则a+≥4不成立,故A错;
a=1,b=1,a2+b2<4ab,故B错,
a=4,b=16,则<,故C错;
由基本不等式得x2+≥2可知D项正确.
故选:D.
【点睛】
本题考查基本不等式应用及其使用条件,考查基本分析求解能力,属基础题.
9.A
【解析】
令,求导可得函数的单调性,进而可得,由可得,即可得出结果.
【详解】
令,则,
当时,,单调递减,当时,,单调递增,
,
,,即.
“”是“”的充分不必要条件.
故选:A.
10.D
【解析】
【分析】
根据基本不等式即可得到答案.
【详解】
因为,所以,则,
当且仅当时取“=”.
故选:D.
11.B
【解析】
根据已知条件,用乘以1,可得,再展开利用基本不等式即可.
【详解】
∵,,,
∴同除得,
∴
当且仅当即时取等号.
【点睛】
本题考查了利用基本不等式求和的最小值,巧用了“1”的乘积,属于基础题.
12.A
【解析】
【详解】
分析:利用直线始终平分圆的周长,可得圆的圆心在直线上,再利用“”的代换,结合基本不等式,即可求出最小值.
详解:因为利用直线
始终平分圆的周长,
所以,圆的圆心在直线上,
,,
,
当且仅当时,等号成立,
即的最小值为,故选A.
点睛:本题主要考查圆的方程与性质,以及利用基本不等式求最值,属于中档题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).
13.B
【解析】
【详解】
分析:根据垂径定理及距离公式得出k,b的关系,再根据基本不等式得出tanα的最小值.
详解:∵圆O的半径为1,被直线y=kx+b(k>0)截得的弦长为,
∴圆心O到直线l的距离d=,即=,
∴b2=,
∴tanα==+≥2=1,当且仅当=即k=1时取等号.
故选B.
点睛:在用基本不等式求最值时,应具备三个条件:一正二定三相等.①一正:关系式中,各项均为正数;②二定:关系式中,含变量的各项的和或积必须有一个为定值;③三相等:含变量的各项均相等,取得最值.
14.B
【解析】
【分析】
设此种商品的价格分别为,第一种方案每次购买这种物品数量为;第二种方案每次购买这种物品的钱数为.则第一种方案的平均价格为;第二种方案的平均价格为,利用基本不等式的性质即可得到答案.
【详解】
设两次购买的单价分别为,方案一平均单价为,
方案二平均单价为,
由均值不等式得.
故第二种购物方式比较经济.
故选:B.
【点睛】
本题考查了利用基本不等式的性质解决实际问题,考查了推理能力与计算能力,属于中档题.
15.C
【解析】
【分析】
由基本不等式可得,通过配方结合可得即可选得答案.
【详解】
,当且仅当时等号成立,
,当时等号成立,
所以.
故选:C
16.A
【解析】
【分析】
设中点为,则利用向量的加法得到,而,,以此求出.然后利用余弦定理和不等式确定C最大时b值,利用勾股定理确定直角三角形后得出面积.
【详解】
设中点为,则
,,即,
由知角为锐角,故 ,
当且仅当,即时最小,又在递减,故最大.此时,恰有,即为直角三角形,,故选.
【点睛】
本题考查了向量的加法减法运算,余弦定理,不等式,勾股定理,比较综合.
17.D
【解析】
由题知,进而①可变形为,②通过取特殊值排除,③通过做差可变形为,④结合基本不等式求解.
【详解】
解:因为,且,
所以,
所以对于①,,故①正确;
对于②,令,显然,故②错误;
对于③,,
由于,所以,所以,故③错误;
对于④,由于,,故④正确.
故选:D.
【点睛】
本题考查不等式的比较大小问题,其中解题的关键在于恒等变形,①,③,,考查运算求解能力与化归转化思想,是中档题.
18.C
【解析】
【分析】
由目标式可得,结合已知条件,应用基本不等式即可求目标式的最小值,注意等号成立的条件.
【详解】
∵,
∴当且仅当时等号成立.
故选:C
19.C
【解析】
【详解】
试题分析:设,由题意,显然时不符合题意,故,则
,可得:
,当且仅当时取等号,故选C.
考点:1.抛物线的简单几何性质;2.均值不等式.
【方法点晴】本题主要考查的是向量在解析几何中的应用及抛物线标准方程方程,均值不等式的灵活运用,属于中档题.解题时一定要注意分析条件,根据条件,利用向量的运算可知,写出直线的斜率,注意均值不等式的使用,特别是要分析等号是否成立,否则易出问题.
20.A
【解析】
【分析】
利用等比数列的通项公式和均值不等式可得结果.
【详解】
由
由为正项数列,可知
再由均值不等式可知
所以
(当且仅当时取等号)
故选:A
【点睛】
本题主要考查等比数列的通项公式及均值不等式,属基础题.
21.C
【解析】
【详解】
函数的图象过点,所以.
.
当且仅当,即,有最小值4.
故选C.
22.A
【解析】
【分析】
根据题设可得,而,利用基本不等式即可求其最大值,注意等号成立的条件.
【详解】
,
∴由题设,,
∵,,
∴,且,
∴当且仅当时等号成立.
故选:A
23.C
【解析】
【分析】
利用基本不等式即可求解.
【详解】
解:,
,
则,
当且仅当时,等号成立,
故的最小值为,
故选:.
24.C
【解析】
【分析】
根据基本不等式和作差比较法,准确运算,即可求解.
【详解】
由题意,实数且,可得,,
又由,
因为,可得,所以,
所以,所以最大值为.
故选:C.
25.D
【解析】
【分析】
利用作差法和基本不等式分析判断每一个选项的正误得解.
【详解】
A. 不一定大于等于零,所以该选项错误;
B. ,当取负数时,显然,所以错误,所以该选项错误;
C. ,当且仅当时成立,由于取得条件不成立,所以,如时,,所以该选项错误;
D. ,当且仅当时取等号.所以该选项正确.
故选:D
【点睛】
本题主要考查基本不等式的应用,意在考查学生对这些知识的理解掌握水平.
26.BD
【解析】
【分析】
根据给定条件举特例可判断A,C;利用不等式性质及均值不等式进行推理可判断B,D作答.
【详解】
对于A,当时,,A错误;
对于B,因,则,于是得,B正确;
对于C,当,时,满足条件,但,C错误;
对于D,由,且得:,当且仅当时取“=”,
而,即,则,于是得,D正确.
故选:BD
27.100
【解析】
【分析】
直接利用基本不等式求解表达式的最大值即可.
【详解】
解:,,且,
则,
当且仅当时取等号,
故答案为:100.
【点睛】
本题主要考查基本不等式求最值,注意等号成立的条件,属于基础题.
28.
【解析】
【分析】
由基本不等式即可求解.
【详解】
因为,所以,
所以取值范围是,
故答案为:
29.6;
【解析】
【分析】
由可得,再利用基本不等式可求出的最小值
【详解】
解:因为,所以,即,
所以,
所以,当且仅当,即时取等号,
所以的最小值为6
故答案为:6
【点睛】
此题考查基本不等式的应用,考查对数的运算性质,属于基础题
30.
【解析】
【分析】
根据补集与交集定义即可求出结果.
【详解】
由于或,又a>b>0,则
故答案为:
31.
【解析】
【详解】
,当且仅当时等号成立,所以的最小值为,故答案为.
【易错点晴】本题主要考查利用基本不等式求最值,属于难题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).
32.4
【解析】
【分析】
由题意结合均值不等式首先求得的最小值,然后结合恒成立的结论得到关于a的不等式,求解不等式即可确定实数a的最小值.
【详解】
,,
当且仅当时等号成立.
由恒成立的条件知,即,解得或(舍去).
.则正实数的最小值为4.
【点睛】
本题主要考查基本不等式的应用,恒成立的结论,不等式的解法等知识,意在考查学生的转化能力和计算求解能力.
33.8
【解析】
根据正数x,y满足,得到,然后由利用基本不等式求解.
【详解】
正数x,y满足,
,
,
当且仅当,即时取等号,
的最小值为8.
故答案为:8.
【点睛】
本题主要考查基本不等式求最值,还考查了转化求解的能力,属于基础题.
34.
【解析】
先由得到,根据基本不等式求出的最小值,得出,求解,即可得出结果.
【详解】
,,且,在等式两边同时除以得,
由基本不等式得,
当且仅当时,等号成立,所以的最小值为,
由于不等式恒成立,则,即,
解得,
故答案为:.
【点睛】
本题考查利用基本不等式处理不等式恒成立问题,同时也考查了一元二次不等式的解法,属于常考题型.
35.
【解析】
首先根据简单线性规划问题的解法求出的最大值,得到的关系,再根据基本不等式中“1”的代换的应用,即可求出.
【详解】
首先作出可行域,如图所示:
把变形为,根据图象可知,当目标函数过点时,
取最大值为1,,代入可得,
则,
当且仅当取等号,可知最小值为.
故答案为:.
【点睛】
本题主要考查基本不等式的应用,涉及“1”的代换技巧,以及简单线性规划问题的解法应用,意在考查学生的数学运算能力和转化能力,属于中档题.
36.
【解析】
【分析】
令分子a取最小值1,分母d 取最大值9,利用基本不等式,求出最小值.
【详解】
,
当且仅当取等号,
故所求式子的最小值为.
【点睛】
利用基本不等式求函数的最值,一定注意满足的条件:一正、二定、三相等.
37.
【解析】
【详解】
试题分析:根据题意有,因为三点共线,所以有,从而有,所以的最小值是.
考点:向量的运算,基本不等式.
【方法点睛】该题考查的是有关应用基本不等式求最值的问题,属于中档题目,在解题的过程中,关键步骤在于对题中条件的转化,根据三点共线,结合向量的性质可知,从而等价于已知两个正数的整式形式和为定值,求分式形式和的最值的问题,两式乘积,最后应用基本不等式求得结果,最后再加,得出最后的答案.
38.
【解析】
【分析】
利用指数运算求得,然后将代数式与相乘,展开后利用基本不等式可求得的最小值.
【详解】
,.
又,,,
当且仅当,时等号成立,所以的最小值是.
故答案为:.
【点睛】
本题考查利用基本不等式求代数式的最值,考查了的妙用,考查计算能力,属于基础题.
39.
【解析】
【分析】
根据题意对函数求二阶导函数,令在区间恒成立,分离参数,解得实数的取值范围即可.
【详解】
在区间上为“凸函数”
在上恒成立
上恒成立
设,,
则
当且仅当时取得最大值,
故答案为:.
【点睛】
本题考查了新定义“凸函数”,考查了分离参数法解决恒成立问题和基本不等式,属于中档题.
40.
【解析】
【分析】
利用基本不等式即可求解.
【详解】
若2x+2y=5,则2≤5,
故2x+y≤,则=≥5×,
当且仅当x=y时“=”成立,
故答案为:.
【点睛】
本题考查了基本不等式求最值,注意运用基本不等式时,验证等号成立的条件,属于基础题.-
41.
【解析】
【分析】
设出P点坐标,P点在直线上即和为定值,积有最大值.
【详解】
设点,由题意,且,即,
则矩形面积,当即时,取“=”.
【点睛】
和为定值,积有最大值.注意:“一正二定三相等”缺一不可.
42.(1);(2).
【解析】
【分析】
(1)设,在中,利用正弦定理求出各边,将问题转化为求角的三角函数的最大值;
(2)利用等面积法,转化为求面积的最大值,利用余弦定理与基本不等式得出, 进而可求得面积的最大值.
【详解】
(1) 因为,,所以,
又,设,,
在中,由正弦定理得,,
所以,,
所以的周长为,.
化简得.
所以当时,的周长有最大值米.
(2)因为图2中与图1中面积相等,
而在中,因为,,,所以.
由余弦定理得,,
所以,,,
所以平方米.
当且仅当时等号成立,
所以花圃面积的最大值为平方米.
43.(1)且;(2)或.
【解析】
【分析】
(1)根据方程有两个不等实根可得,解不等式组即可得解;
(2)将,代入到,然后分离常数,再对和进行分类讨论,结合基本不等式即可得解.
【详解】
(1)∵方程有两个不等实根
∴方程有两个不等实根
∴,解得且
(2),
∴,,
当时,即,则,当且仅当,即时取等号;
当时,即,则,当且仅当,即时取等号,则.
综上,的取值范围为或.
44.(1);(2);(3)
【解析】
(1)由题可知,则;
(2)将平方即可求出最大值;
(3)将代入,即可根据二次函数的性质求出最值.
【详解】
(1),
,当且仅当时等号成立,
,
的最小值为;
(2),
,即的最大值为;
(3),,
则,
当时,取得最小值.
【点睛】
本题考查基本不等式的应用,属于基础题.
45.(1)(2)的位置应该在米.且的最小值为米.
【解析】
【详解】
分析:(1)由三角形面积公式可得,在中,由余弦定理得;(2)由基本不等式可得,当且仅当即米时“=”成立,从而可得结果.
详解:(1)∵的边长是米,在上,
则
∴
故,
在中,由余弦定理得:
(2)若作为输水管道,则需求的最小值
∴
当且仅当即米时“=”成立
∴的位置应该在米.
且的最小值为米.
点睛:本题主要考查阅读能力、数学建模能力和化归思想以及余弦定理和基本不等式求最值,属于难题. 与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际问题转化为数学模型进行解答.
46.(1)证明见解析;(2)证明见解析.
【解析】
【分析】
(1)运用作差比较法得,由此可得证;
(2)作差,判断符号得,由此可得证.
【详解】
证明:(1)因为,又bc-ad≥0,bd>0,
所以,所以;
(2)因为,又a>0,b>0,所以,所以.
47.(1);(2)证明见解析.
【解析】
(1)利用基本不等式的变形形式(时取等号)求得的最大值,即得的最小值;
(2) 先利用“乘1法”转化,使用基本不等式证得,在利用基本不等式的变形形式证得.
【详解】
解:(1)因为,,,
由基本不等式得,当且仅当时取等号.
因为恒成立,所以,的最小值为.
(2)因为,
所以
当且仅当时取等号,得证.
【点睛】
关键点点睛:(1)基本不等式的变形形式要熟练掌握和运用;(2)先利用“乘1法”转化,使用基本不等式求最值更是已知和为定值求倒数和最值的有利方法.
48.(1) (2)宽为,高为
【解析】
【分析】
(1)根据题意设上栏框内高度为,下栏框内高度为,则,,即可表示出透光面积;
(2)根据基本不等式,等号成立的时刻即为所求.
【详解】
解:(1)铝合金窗的宽和高分别为,,,,
由已知,①
设上栏框内高度为,下栏框内高度为,
则,,
所以透光部分的面积
;
(2)因为,,
所以,
所以,
当且仅当时等号成立,此时,
代入①式得,从而,
即当,时,取得最大值.
答:铝合金窗的宽度为,高为时,可使透光部分的面积最大.
【点睛】
此题考查函数模型的建立,根据函数关系利用基本不等式或勾型函数单调性求解最值.
49.(1);(2)当毫米时,总费用最小,最小值为180万元.
【解析】
【分析】
(1)依题意,x=10时,C(10)=,求得k值,得到C(x)=,则f(x)的解析式可求;
(2)由(1)得f(x)=10x+,变形后利用基本不等式求最值.
【详解】
(1)依题意,x=10时,C(10)=,解得k=36,
∴C(x)=,则f(x)=10x+=10x+,x∈[10,15];
(2)由(1)得f(x)=10x+=10x-60+,
=10(x-6)+,
当且仅当10(x-6)=,即x=12时取最小值,
答:当x=12毫米时,总费用f(x)最小,最小值为180万元.
【点睛】
本题考查简单的数学建模思想方法,训练了利用基本不等式求最值,是中档题.
试卷第页,共页
试卷第页,共页
一、单选题
1.下列各函数中,最小值为4的是( )
A. B.
C. D.
2.设,,则的最小值为( )
A. B. C. D.
3.已知,,,则的最小值是( ).
A.3 B. C. D.9
4.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明,现有如图所示图形,点在半圆上,点在直径上,且,设,,则该图形可以完成的无字证明为( )
A. B.
C. D.
5.已知抛物线的焦点为,为坐标原点,设为抛物线上的动点,则的最大值为
A. B. C. D.
6.双曲线的离心率是,则的最小值为
A. B. C. D.
7.若,则下列不等式成立的是( ).A. B.
C. D.
8.下列不等式中,正确的是( )
A.a+≥4 B.a2+b2≥4ab
C.≥ D.x2+≥2
9.若函数,的图象都是一条连续不断的曲线,定义:.若函数和的定义域是,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.若,则当取得最大值时,x的值为( )
A.1 B. C. D.
11.已知,,,则的最小值为( )
A. B.1 C.2 D.4
12.若直线(,)平分圆的周长,则的最小值为
A. B. C. D.
13.在平面直角坐标系中,圆被直线()截得的弦长为,角的始边是轴的非负半轴,终边过点,则的最小值
A. B.1 C. D.2
14.小明同学计划两次购买同种笔芯(两次笔芯的单价不同),有两种方案:第一种方法是每次购买笔芯数量一定;第二种方法是每次购买笔芯所花钱数一定.则哪种购买方式比较经济( )
A.第一种 B.第二种
C.两种一样 D.无法判断
15.已知P=a2+(a≠0),Q=b2-4b+7(1<b≤3).则P、Q的大小关系为( )
A.P>Q B.P<Q C.P≥Q D.P≤Q
16.已知在中,角,,所对的边分别为,,,且,点为其外接圆的圆心.已知,则当角取到最大值时的面积为
A. B. C. D.
17.若,且,则下列结论一定正确的是( )
①②③④
A.①② B.②③ C.①③ D.①④
18.已知,则的最小值是( )
A.1 B.4 C.7 D.
19.设为坐标原点,是以为焦点的抛物线上任意一点,是线段上的点,且,则直线的斜率的最大值为
A. B. C. D.1
20.已知正数组成的等比数列的前8项的积是81,那么的最小值是( )
A. B. C.8 D.6
21.已知均为正实数,函数的图象过点,则的最小值为
A.2 B.3 C.4 D.5
22.已知,,,则的最大值为( )
A. B. C.1 D.
23.若,则的最小值为( )
A. B. C. D.
24.若且,则,,,中的最大值的是( )
A. B. C. D.
25.下列不等式中正确的是( )
A. B. C. D.
二、多选题
26.若,且,则( )
A. B.
C. D.
三、填空题
27.已知,且,则xy的最大值为___________
28.若、是实数,且,则取值范围是______.
29.若正实数满足,则的最小值为_____.
30.已知全集U=R,实数a,b满足a>b>0,集合M={x|<x<a},N={x|b},则_________
31.已知正数满足,则的最小值为________.
32.已知不等式对任意正实数,恒成立,则正实数的最小值为______.
33.已知正数x,y满足,则的最小值为________
34.已知,,且,若恒成立,则实数t的取值范围是________.
35.已知满足约束条件,且的最大值为1,则的最小值为________.
36.若,则的最小值为 __________.
37.如图,在△ABC中,E为边AC上一点,且,P为BE上一点,且满足,则的最小值为______.
38.已知,,,则的最小值是______.
39.定义:设函数在上的导函数为,若在上也存在导函数,则称函数在上存在二阶导函数,简记为.若在区间上,则称函数在区间上为“凸函数”.已知在区间上为“凸函数”,则实数的取值范围为______.
40.若,则的最小值为__.
41.已知一次函数图象与轴、轴分别交于点、,点在线段上,轴于点,轴于点,则矩形面积的最大值是_____________ ;
四、解答题
42.邳州市沙沟湖水杉公园为了更好的服务游客,对赏柳观光区进行改造升级.如图,已知扇形是一个观光区的平面示意图,其中扇形半径为10米,,为了便于游客观光和旅游,提出以下两种设计方案:
(1)如图1,拟在观光区内规划一条三角形形状的道路,道路的一个顶点在弧上,另一顶点在半径上,且,求周长的最大值;
(2)如图2,拟在观光区规划一个三角形区域种植花卉,三角形花圃的一个顶点在弧上,另两个顶点在半径上,且,求花圃面积的最大值.
43.已知.
(1)若方程有两个不等实根,求实数的范围;
(2)当,时,求的取值范围.
44.已知x+y=1,x,y∈R+.
(1)求x2+y2+xy的最小值;
(2)求的最大值;
(3)求x(1-3y)的最小值.
45.选修4-4:坐标系与参数方程
某县一中计划把一块边长为米的等边的边角地开辟为植物新品种实验基地,图4中需要把基地分成面积相等的两部分,在上,在上.
(1)设,使用表示的函数关系式;
(2)如果是灌溉输水管道的位置,为了节约,的位置应该在哪里?求出最小值.
46.证明下列不等式
(1)若bc-ad≥0,bd>0,求证:
(2)已知a>0,b>0,求证:
47.已知为正实数,且满足.
(1)若恒成立,求的最小值;
(2)证明:.
48.如图1,一个铝合金窗是由一个框架和部分外推窗框组成,其中框架设计如图2,其结构为上、下两栏,下栏为两个完全相同的矩形,四周框架和中间隔栏的材料为铝合金,宽均为,上栏和下栏的框内矩形高度(不含铝合金部分)比为,此铝合金窗占用的墙面面积为,设该铝合金窗的宽和高分别,,铝合金的透光部分的面积为(外推窗框遮挡光线部分忽略不计).
(1)试用,表示;
(2)若要使最大,则铝合金窗的宽和高分别为多少?
49.为迎接2018年省运会,宁德市某体育馆需要重新铺设塑胶跑道.已知每毫米厚的跑道的铺设成本为10万元,跑道平均每年的维护费C(单位:万元)与跑道厚度x(单位:毫米)的关系为C(x)=,x∈[10,15].若跑道厚度为10毫米,则平均每年的维护费需要9万元.设总费用f(x)为跑道铺设费用与10年维护费之和.
(1)求k的值与总费用f(x)的表达式;
(2)塑胶跑道铺设多厚时,总费用f(x)最小,并求最小值.
试卷第页,共页
试卷第页,共页
参考答案:
1.D
【解析】
【分析】
直接利用基本不等式.和关系式的恒等变换的应用求出结果.
【详解】
解:用基本不等式要满足“一正二定三相等“.
.选项中的正负不确定.同样的,
,选项中和取值不一定大于0.
.当时,,,,
时不符合,所以也不能用基本不等式,不满足三相等,
.,且,
当且仅当即时取等号.
故选:.
【点睛】
本题考查的知识要点:直接利用基本不等式的性质的应用和用基本不等式要满足“一正二定三相等“.的条件的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
2.B
【解析】
利用,,,且;
对进行分类讨论,分为和,进行讨论,
然后,求解即可得到的最小值
【详解】
,,,且;
当,;当且仅当
,又,解得或,又由,得时,此时,,的最小值;
当,,当且仅当时,解得或,又由,得,此时,,的最小值;
综上,的最小值;
故选:B
【点睛】
关键点睛:解题的关键在于利用,,,可得且,对进行分类讨论,难点在于利用基本不等式进行求最值,本题属于中档题
3.B
【解析】
【分析】
由已知结合指数与对数的运算性质可得,从而,展开后利用基本不等式可得解.
【详解】
,,,
所以,即,
所以,
则,
当且仅当且即,时取等号,
则的最小值是.
故选.
【点睛】
本题主要考查了指数与对数的运算性质及利用基本不等式求解最值,要注意应用条件的配凑.
4.B
【解析】
【分析】
由图形可知:,在直角中,利用勾股定理求得,结合,即可求解.
【详解】
由图形可知:,
在直角中,利用勾股定理,可得,
因为,所以.
故选:B.
5.D
【解析】
【分析】
由抛物线方程为:y2=2px(p>0),可得:焦点F(,0),由抛物线的定义可得,化简再换元,利用基本不等式求得最大值.
【详解】
由抛物线方程为:y2=2px(p>0),可得:
焦点F(,0),
设M(m,n),则n2=2pm,m>0,设M 到准线x的距离等于d,
则.
令 pmt,t,则 m,
∴(当且仅当 t 时,等号成立).
故的最大值为,
故选D.
【点睛】
本题考查抛物线的定义、基本不等式的应用,考查换元的思想,解题的关键是表达出,再利用基本不等式,综合性强.
6.C
【解析】
【详解】
,则,当即时取最小值,故选C.
【易错点晴】本题主要考查双曲线的离心率及利用基本不等式求最值,属于难题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).
7.B
【解析】
直接根据基本不等式判断即可.
【详解】
因为,
所以,当且仅当时等号成立,
由,
所以,
故选:B
8.D
【解析】
【分析】
举例说明ABC错误,利用基本不等式证明D成立.
【详解】
a<0,则a+≥4不成立,故A错;
a=1,b=1,a2+b2<4ab,故B错,
a=4,b=16,则<,故C错;
由基本不等式得x2+≥2可知D项正确.
故选:D.
【点睛】
本题考查基本不等式应用及其使用条件,考查基本分析求解能力,属基础题.
9.A
【解析】
令,求导可得函数的单调性,进而可得,由可得,即可得出结果.
【详解】
令,则,
当时,,单调递减,当时,,单调递增,
,
,,即.
“”是“”的充分不必要条件.
故选:A.
10.D
【解析】
【分析】
根据基本不等式即可得到答案.
【详解】
因为,所以,则,
当且仅当时取“=”.
故选:D.
11.B
【解析】
根据已知条件,用乘以1,可得,再展开利用基本不等式即可.
【详解】
∵,,,
∴同除得,
∴
当且仅当即时取等号.
【点睛】
本题考查了利用基本不等式求和的最小值,巧用了“1”的乘积,属于基础题.
12.A
【解析】
【详解】
分析:利用直线始终平分圆的周长,可得圆的圆心在直线上,再利用“”的代换,结合基本不等式,即可求出最小值.
详解:因为利用直线
始终平分圆的周长,
所以,圆的圆心在直线上,
,,
,
当且仅当时,等号成立,
即的最小值为,故选A.
点睛:本题主要考查圆的方程与性质,以及利用基本不等式求最值,属于中档题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).
13.B
【解析】
【详解】
分析:根据垂径定理及距离公式得出k,b的关系,再根据基本不等式得出tanα的最小值.
详解:∵圆O的半径为1,被直线y=kx+b(k>0)截得的弦长为,
∴圆心O到直线l的距离d=,即=,
∴b2=,
∴tanα==+≥2=1,当且仅当=即k=1时取等号.
故选B.
点睛:在用基本不等式求最值时,应具备三个条件:一正二定三相等.①一正:关系式中,各项均为正数;②二定:关系式中,含变量的各项的和或积必须有一个为定值;③三相等:含变量的各项均相等,取得最值.
14.B
【解析】
【分析】
设此种商品的价格分别为,第一种方案每次购买这种物品数量为;第二种方案每次购买这种物品的钱数为.则第一种方案的平均价格为;第二种方案的平均价格为,利用基本不等式的性质即可得到答案.
【详解】
设两次购买的单价分别为,方案一平均单价为,
方案二平均单价为,
由均值不等式得.
故第二种购物方式比较经济.
故选:B.
【点睛】
本题考查了利用基本不等式的性质解决实际问题,考查了推理能力与计算能力,属于中档题.
15.C
【解析】
【分析】
由基本不等式可得,通过配方结合可得即可选得答案.
【详解】
,当且仅当时等号成立,
,当时等号成立,
所以.
故选:C
16.A
【解析】
【分析】
设中点为,则利用向量的加法得到,而,,以此求出.然后利用余弦定理和不等式确定C最大时b值,利用勾股定理确定直角三角形后得出面积.
【详解】
设中点为,则
,,即,
由知角为锐角,故 ,
当且仅当,即时最小,又在递减,故最大.此时,恰有,即为直角三角形,,故选.
【点睛】
本题考查了向量的加法减法运算,余弦定理,不等式,勾股定理,比较综合.
17.D
【解析】
由题知,进而①可变形为,②通过取特殊值排除,③通过做差可变形为,④结合基本不等式求解.
【详解】
解:因为,且,
所以,
所以对于①,,故①正确;
对于②,令,显然,故②错误;
对于③,,
由于,所以,所以,故③错误;
对于④,由于,,故④正确.
故选:D.
【点睛】
本题考查不等式的比较大小问题,其中解题的关键在于恒等变形,①,③,,考查运算求解能力与化归转化思想,是中档题.
18.C
【解析】
【分析】
由目标式可得,结合已知条件,应用基本不等式即可求目标式的最小值,注意等号成立的条件.
【详解】
∵,
∴当且仅当时等号成立.
故选:C
19.C
【解析】
【详解】
试题分析:设,由题意,显然时不符合题意,故,则
,可得:
,当且仅当时取等号,故选C.
考点:1.抛物线的简单几何性质;2.均值不等式.
【方法点晴】本题主要考查的是向量在解析几何中的应用及抛物线标准方程方程,均值不等式的灵活运用,属于中档题.解题时一定要注意分析条件,根据条件,利用向量的运算可知,写出直线的斜率,注意均值不等式的使用,特别是要分析等号是否成立,否则易出问题.
20.A
【解析】
【分析】
利用等比数列的通项公式和均值不等式可得结果.
【详解】
由
由为正项数列,可知
再由均值不等式可知
所以
(当且仅当时取等号)
故选:A
【点睛】
本题主要考查等比数列的通项公式及均值不等式,属基础题.
21.C
【解析】
【详解】
函数的图象过点,所以.
.
当且仅当,即,有最小值4.
故选C.
22.A
【解析】
【分析】
根据题设可得,而,利用基本不等式即可求其最大值,注意等号成立的条件.
【详解】
,
∴由题设,,
∵,,
∴,且,
∴当且仅当时等号成立.
故选:A
23.C
【解析】
【分析】
利用基本不等式即可求解.
【详解】
解:,
,
则,
当且仅当时,等号成立,
故的最小值为,
故选:.
24.C
【解析】
【分析】
根据基本不等式和作差比较法,准确运算,即可求解.
【详解】
由题意,实数且,可得,,
又由,
因为,可得,所以,
所以,所以最大值为.
故选:C.
25.D
【解析】
【分析】
利用作差法和基本不等式分析判断每一个选项的正误得解.
【详解】
A. 不一定大于等于零,所以该选项错误;
B. ,当取负数时,显然,所以错误,所以该选项错误;
C. ,当且仅当时成立,由于取得条件不成立,所以,如时,,所以该选项错误;
D. ,当且仅当时取等号.所以该选项正确.
故选:D
【点睛】
本题主要考查基本不等式的应用,意在考查学生对这些知识的理解掌握水平.
26.BD
【解析】
【分析】
根据给定条件举特例可判断A,C;利用不等式性质及均值不等式进行推理可判断B,D作答.
【详解】
对于A,当时,,A错误;
对于B,因,则,于是得,B正确;
对于C,当,时,满足条件,但,C错误;
对于D,由,且得:,当且仅当时取“=”,
而,即,则,于是得,D正确.
故选:BD
27.100
【解析】
【分析】
直接利用基本不等式求解表达式的最大值即可.
【详解】
解:,,且,
则,
当且仅当时取等号,
故答案为:100.
【点睛】
本题主要考查基本不等式求最值,注意等号成立的条件,属于基础题.
28.
【解析】
【分析】
由基本不等式即可求解.
【详解】
因为,所以,
所以取值范围是,
故答案为:
29.6;
【解析】
【分析】
由可得,再利用基本不等式可求出的最小值
【详解】
解:因为,所以,即,
所以,
所以,当且仅当,即时取等号,
所以的最小值为6
故答案为:6
【点睛】
此题考查基本不等式的应用,考查对数的运算性质,属于基础题
30.
【解析】
【分析】
根据补集与交集定义即可求出结果.
【详解】
由于或,又a>b>0,则
故答案为:
31.
【解析】
【详解】
,当且仅当时等号成立,所以的最小值为,故答案为.
【易错点晴】本题主要考查利用基本不等式求最值,属于难题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).
32.4
【解析】
【分析】
由题意结合均值不等式首先求得的最小值,然后结合恒成立的结论得到关于a的不等式,求解不等式即可确定实数a的最小值.
【详解】
,,
当且仅当时等号成立.
由恒成立的条件知,即,解得或(舍去).
.则正实数的最小值为4.
【点睛】
本题主要考查基本不等式的应用,恒成立的结论,不等式的解法等知识,意在考查学生的转化能力和计算求解能力.
33.8
【解析】
根据正数x,y满足,得到,然后由利用基本不等式求解.
【详解】
正数x,y满足,
,
,
当且仅当,即时取等号,
的最小值为8.
故答案为:8.
【点睛】
本题主要考查基本不等式求最值,还考查了转化求解的能力,属于基础题.
34.
【解析】
先由得到,根据基本不等式求出的最小值,得出,求解,即可得出结果.
【详解】
,,且,在等式两边同时除以得,
由基本不等式得,
当且仅当时,等号成立,所以的最小值为,
由于不等式恒成立,则,即,
解得,
故答案为:.
【点睛】
本题考查利用基本不等式处理不等式恒成立问题,同时也考查了一元二次不等式的解法,属于常考题型.
35.
【解析】
首先根据简单线性规划问题的解法求出的最大值,得到的关系,再根据基本不等式中“1”的代换的应用,即可求出.
【详解】
首先作出可行域,如图所示:
把变形为,根据图象可知,当目标函数过点时,
取最大值为1,,代入可得,
则,
当且仅当取等号,可知最小值为.
故答案为:.
【点睛】
本题主要考查基本不等式的应用,涉及“1”的代换技巧,以及简单线性规划问题的解法应用,意在考查学生的数学运算能力和转化能力,属于中档题.
36.
【解析】
【分析】
令分子a取最小值1,分母d 取最大值9,利用基本不等式,求出最小值.
【详解】
,
当且仅当取等号,
故所求式子的最小值为.
【点睛】
利用基本不等式求函数的最值,一定注意满足的条件:一正、二定、三相等.
37.
【解析】
【详解】
试题分析:根据题意有,因为三点共线,所以有,从而有,所以的最小值是.
考点:向量的运算,基本不等式.
【方法点睛】该题考查的是有关应用基本不等式求最值的问题,属于中档题目,在解题的过程中,关键步骤在于对题中条件的转化,根据三点共线,结合向量的性质可知,从而等价于已知两个正数的整式形式和为定值,求分式形式和的最值的问题,两式乘积,最后应用基本不等式求得结果,最后再加,得出最后的答案.
38.
【解析】
【分析】
利用指数运算求得,然后将代数式与相乘,展开后利用基本不等式可求得的最小值.
【详解】
,.
又,,,
当且仅当,时等号成立,所以的最小值是.
故答案为:.
【点睛】
本题考查利用基本不等式求代数式的最值,考查了的妙用,考查计算能力,属于基础题.
39.
【解析】
【分析】
根据题意对函数求二阶导函数,令在区间恒成立,分离参数,解得实数的取值范围即可.
【详解】
在区间上为“凸函数”
在上恒成立
上恒成立
设,,
则
当且仅当时取得最大值,
故答案为:.
【点睛】
本题考查了新定义“凸函数”,考查了分离参数法解决恒成立问题和基本不等式,属于中档题.
40.
【解析】
【分析】
利用基本不等式即可求解.
【详解】
若2x+2y=5,则2≤5,
故2x+y≤,则=≥5×,
当且仅当x=y时“=”成立,
故答案为:.
【点睛】
本题考查了基本不等式求最值,注意运用基本不等式时,验证等号成立的条件,属于基础题.-
41.
【解析】
【分析】
设出P点坐标,P点在直线上即和为定值,积有最大值.
【详解】
设点,由题意,且,即,
则矩形面积,当即时,取“=”.
【点睛】
和为定值,积有最大值.注意:“一正二定三相等”缺一不可.
42.(1);(2).
【解析】
【分析】
(1)设,在中,利用正弦定理求出各边,将问题转化为求角的三角函数的最大值;
(2)利用等面积法,转化为求面积的最大值,利用余弦定理与基本不等式得出, 进而可求得面积的最大值.
【详解】
(1) 因为,,所以,
又,设,,
在中,由正弦定理得,,
所以,,
所以的周长为,.
化简得.
所以当时,的周长有最大值米.
(2)因为图2中与图1中面积相等,
而在中,因为,,,所以.
由余弦定理得,,
所以,,,
所以平方米.
当且仅当时等号成立,
所以花圃面积的最大值为平方米.
43.(1)且;(2)或.
【解析】
【分析】
(1)根据方程有两个不等实根可得,解不等式组即可得解;
(2)将,代入到,然后分离常数,再对和进行分类讨论,结合基本不等式即可得解.
【详解】
(1)∵方程有两个不等实根
∴方程有两个不等实根
∴,解得且
(2),
∴,,
当时,即,则,当且仅当,即时取等号;
当时,即,则,当且仅当,即时取等号,则.
综上,的取值范围为或.
44.(1);(2);(3)
【解析】
(1)由题可知,则;
(2)将平方即可求出最大值;
(3)将代入,即可根据二次函数的性质求出最值.
【详解】
(1),
,当且仅当时等号成立,
,
的最小值为;
(2),
,即的最大值为;
(3),,
则,
当时,取得最小值.
【点睛】
本题考查基本不等式的应用,属于基础题.
45.(1)(2)的位置应该在米.且的最小值为米.
【解析】
【详解】
分析:(1)由三角形面积公式可得,在中,由余弦定理得;(2)由基本不等式可得,当且仅当即米时“=”成立,从而可得结果.
详解:(1)∵的边长是米,在上,
则
∴
故,
在中,由余弦定理得:
(2)若作为输水管道,则需求的最小值
∴
当且仅当即米时“=”成立
∴的位置应该在米.
且的最小值为米.
点睛:本题主要考查阅读能力、数学建模能力和化归思想以及余弦定理和基本不等式求最值,属于难题. 与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际问题转化为数学模型进行解答.
46.(1)证明见解析;(2)证明见解析.
【解析】
【分析】
(1)运用作差比较法得,由此可得证;
(2)作差,判断符号得,由此可得证.
【详解】
证明:(1)因为,又bc-ad≥0,bd>0,
所以,所以;
(2)因为,又a>0,b>0,所以,所以.
47.(1);(2)证明见解析.
【解析】
(1)利用基本不等式的变形形式(时取等号)求得的最大值,即得的最小值;
(2) 先利用“乘1法”转化,使用基本不等式证得,在利用基本不等式的变形形式证得.
【详解】
解:(1)因为,,,
由基本不等式得,当且仅当时取等号.
因为恒成立,所以,的最小值为.
(2)因为,
所以
当且仅当时取等号,得证.
【点睛】
关键点点睛:(1)基本不等式的变形形式要熟练掌握和运用;(2)先利用“乘1法”转化,使用基本不等式求最值更是已知和为定值求倒数和最值的有利方法.
48.(1) (2)宽为,高为
【解析】
【分析】
(1)根据题意设上栏框内高度为,下栏框内高度为,则,,即可表示出透光面积;
(2)根据基本不等式,等号成立的时刻即为所求.
【详解】
解:(1)铝合金窗的宽和高分别为,,,,
由已知,①
设上栏框内高度为,下栏框内高度为,
则,,
所以透光部分的面积
;
(2)因为,,
所以,
所以,
当且仅当时等号成立,此时,
代入①式得,从而,
即当,时,取得最大值.
答:铝合金窗的宽度为,高为时,可使透光部分的面积最大.
【点睛】
此题考查函数模型的建立,根据函数关系利用基本不等式或勾型函数单调性求解最值.
49.(1);(2)当毫米时,总费用最小,最小值为180万元.
【解析】
【分析】
(1)依题意,x=10时,C(10)=,求得k值,得到C(x)=,则f(x)的解析式可求;
(2)由(1)得f(x)=10x+,变形后利用基本不等式求最值.
【详解】
(1)依题意,x=10时,C(10)=,解得k=36,
∴C(x)=,则f(x)=10x+=10x+,x∈[10,15];
(2)由(1)得f(x)=10x+=10x-60+,
=10(x-6)+,
当且仅当10(x-6)=,即x=12时取最小值,
答:当x=12毫米时,总费用f(x)最小,最小值为180万元.
【点睛】
本题考查简单的数学建模思想方法,训练了利用基本不等式求最值,是中档题.
试卷第页,共页
试卷第页,共页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
