选修3-1 1.9 带电粒子在电场中的运动 同步练习(word含答案)
文档属性
| 名称 | 选修3-1 1.9 带电粒子在电场中的运动 同步练习(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 507.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-22 04:57:20 | ||
图片预览


文档简介
选修3-1 1.9 带电粒子在电场中的运动 同步练习
一、单项选择题(共10小题;共40分)
1. 如图()所示的两平行金属板 、 间加上图()所示电压, 时, 板电势比 板高 ,在两板正中央 点放一电子,初速度为零,电子只受静电力而运动,且不会碰到金属板,则这个电子处于 点右侧、速度向右,且速度逐渐减小的时间段是
A. B.
C. D.
2. 如图所示,在真空中有一对带电的平行金属板水平放置。一带电粒子沿平行于板面的方向,从左侧两极板中央射入电场中,恰能从右侧极板边缘处离开电场。不计粒子重力。若可以改变某个量,下列哪种变化,仍能确保粒子一定飞出电场
A. 只增大粒子的带电量 B. 只增大电场强度
C. 只减小粒子的比荷 D. 只减小粒子的入射速度
3. 图 所示为示波管的原理图。如果在电极 之间所加的电压按图 所示的规律变化,在电极 之间所加的电压按图 所示的规律变化,则在荧光屏上会看到的图形是
A. B.
C. D.
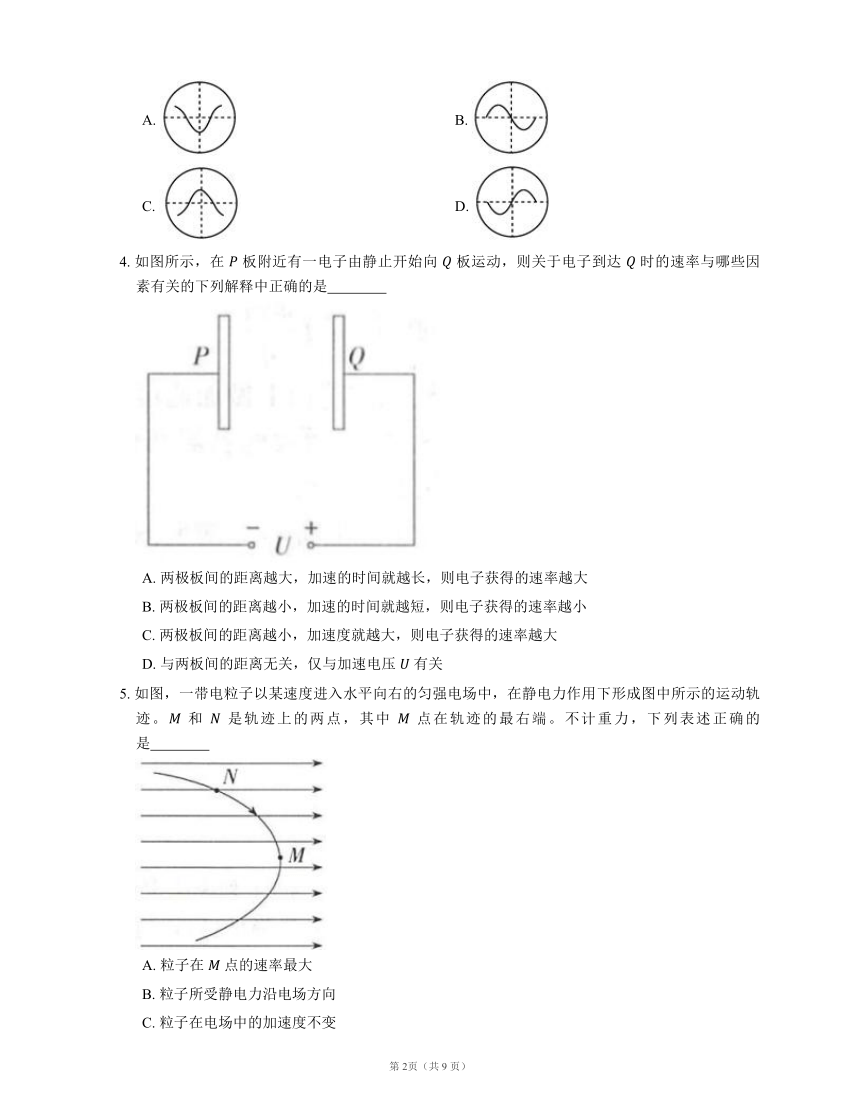
4. 如图所示,在 板附近有一电子由静止开始向 板运动,则关于电子到达 时的速率与哪些因素有关的下列解释中正确的是
A. 两极板间的距离越大,加速的时间就越长,则电子获得的速率越大
B. 两极板间的距离越小,加速的时间就越短,则电子获得的速率越小
C. 两极板间的距离越小,加速度就越大,则电子获得的速率越大
D. 与两板间的距离无关,仅与加速电压 有关
5. 如图,一带电粒子以某速度进入水平向右的匀强电场中,在静电力作用下形成图中所示的运动轨迹。 和 是轨迹上的两点,其中 点在轨迹的最右端。不计重力,下列表述正确的是
A. 粒子在 点的速率最大
B. 粒子所受静电力沿电场方向
C. 粒子在电场中的加速度不变
D. 粒子在电场中的电势能始终在增加
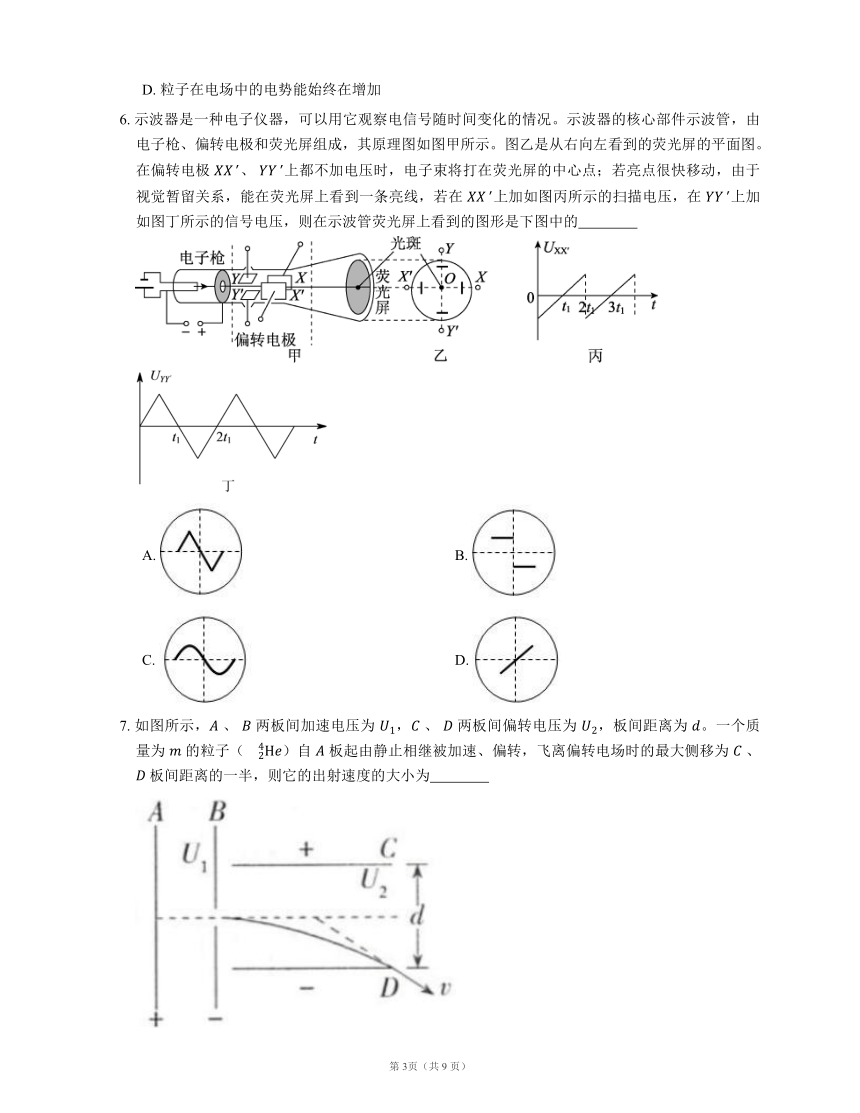
6. 示波器是一种电子仪器,可以用它观察电信号随时间变化的情况。示波器的核心部件示波管,由电子枪、偏转电极和荧光屏组成,其原理图如图甲所示。图乙是从右向左看到的荧光屏的平面图。在偏转电极 、 上都不加电压时,电子束将打在荧光屏的中心点;若亮点很快移动,由于视觉暂留关系,能在荧光屏上看到一条亮线,若在 上加如图丙所示的扫描电压,在 上加如图丁所示的信号电压,则在示波管荧光屏上看到的图形是下图中的
A. B.
C. D.
7. 如图所示, 、 两板间加速电压为 , 、 两板间偏转电压为 ,板间距离为 。一个质量为 的粒子()自 板起由静止相继被加速、偏转,飞离偏转电场时的最大侧移为 、 板间距离的一半,则它的出射速度的大小为
A. B. C. D.
8. 如图所示,一价氢离子、一价氦离子和二价氦离子的混合物以相同的初速度沿垂直匀强电场的方向进入同一偏转电场,且经过偏转后都从右侧离开了电场,则三种粒子相同的是
A. 离开偏转电场时的动能 B. 在偏转电场中的时间
C. 在偏转电场中偏转的角度 D. 在偏转电场中的侧移量
9. 如图甲所示为示波管原理图。如果在电极 之间所加的电压按图乙所的规律变化,在电极 之间所加的电压按图丙所示的规律变化,则在荧光屏上会看到的图形是选项中的
A. B.
C. D.
10. 如图甲所示,两平行正对的金属板 、 间加有如图乙所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间 处。若在 时刻释放该粒子,粒子会时而向 板运动,时而向 板运动,并最终打在 板上。则 应满足
A. B. C. D.
二、填空题(共4小题;共24分)
11. 示波管的基本原理:电子在加速电场中被 ,在偏转电场中被 。电子枪的作用是:产生高速飞行的一束电子。偏转电极 上加的是待显示的 电压, 电极上接入仪器自身产生的锯齿形电压,叫做 电压。
12. 电荷量为 、质量为 的正离子 ,电荷量为 、质量为 的正离子 ,均由静止开始经相同电压加速后, 、 动能之比 ,速度大小之比 。
13. 如图是示波管的原理图.它由电子枪、偏转电极( 和 )、荧光屏组成,管内抽成真空.给电子枪通电后,如果在偏转电极 和 上都没有加电压,电子束将打在荧光屏的中心 点.
(1)带电粒子在 区域是加速的,在 区域是偏转的.
(2)若 ,,则粒子向 板偏移,若 ,,则粒子向 板偏移.
14. 如图所示,有一圆心为 ,半径为 的圆, 为圆的直径,在圆形区域所在空间有匀强电场。将质量为 ,电荷量为 的正点电荷由 点静止释放,自圆周上的 点以速率 穿出,已知 与 的夹角 ,运动中点电荷仅受电场力的作用,则匀强电场的场强大小为 ;若将该点电荷从 点移到圆周上的任意一点,则其中点电荷电势能变化的最大值是 。
三、解答题(共3小题;共39分)
15. 如图所示,两组平行带电金属板,一组竖直放置,两板间所加电压为 ,另一组水平放置,板长为 ,两板间的距离为 ,有一个质量为 ,带电荷量为 微粒,从紧靠竖直板上的 点由静止释放后,经 点进入水平金属板并从两板间射出。 点位于两水平金属板的正中间,微粒所受重力忽略不计,求。
(1)该微粒通过 点时的速度大小。
(2)该微粒通过水平金属板的时间。
(3)为使该微粒从两极板射出时的动量最大,加在水平金属板间的电压 应为多大。
16. 如图所示为一示波管的示意图,阴极 和阳极 间加速电压为 ,偏转板 和 间偏转电压为 ,偏转板间距离为 ,板长为 。偏转板中点到荧光屏的距离为 ,从阴极发射出的电子(初速度视为零),经加速和偏转后打在屏上 点,求电子打在屏上的侧移量 。(忽略电子所受重力,不计电子之间的相互作用)
17. 如图所示,带电金属板 、 竖直平行正对放置, 板中心的小孔正好位于平面直角坐标系 的 点, 轴沿竖直方向。在 的区域内存在沿 轴正方向的匀强电场,电场强度大小为 ;比荷为 的带正电的粒子 从 板中心 处由静止释放,其运动轨迹恰好经过 点。粒子 的重力不计。
(1)求金属板 、 之间的电势差 ;
(2)若在粒子 经过 点的同时,在 轴右侧匀强电场中某点由静止释放另一带电粒子 ,使 、 恰能在运动中相碰;假设 的质量是 的 倍,带电情况与 相同,粒子 的重力及 、 之间的相互作用力均忽略不计,求粒子 释放点的横纵坐标 、 应满足的函数关系。
答案
第一部分
1. B
【解析】在 时间内, 板电势比 板高 ,所以电场方向水平向左,电子所受静电力方向向右,加速度方向也向右,所以电子从 点向右做匀加速直线运动,选项A错误;
在 时间内, 板电势比 板低 ,电场强度方向水平向右,所以电子所受静电力方向向左,加速度方向也向左,所以电子向右做匀减速直线运动,当 时速度为零,此时电子在 点的右侧,选项B正确;
在 时间内, 板电势比 板低 ,电场强度方向水平向右,所以电子所受静电力方向向左,加速度方向也向左,所以电子向左做匀加速直线运动,选项C错误;
在 时间内, 板电势比 板高 ,电场强度方向水平向左,所以电子所受静电力方向向右,加速度方向也向右,所以电子向左做匀减速直线运动,到 时刻速度为零,恰好又回到 点,选项D错误。
2. C
【解析】竖直方向偏转距离 ,,,所以 。
增加, 增大,故飞不出,A错误;
增大, 增大,故飞不出,B错误;
减小, 减小,故能飞出,C正确;
减小, 增大,故飞不出,D错误。
3. B
【解析】在 时间内,扫描电压扫描一次,信号电压完成一个周期,当 为正的最大值时,电子打在荧光屏上有正的最大位移,当 为负的最大值时,电子打在荧光屏上有负的最大位移,因此一个周期内荧光屏上的图象为 B 项。
4. D
【解析】由 可知,电子到达 板时的速率与两板间距离无关,仅与加速电压 有关,因电压不变,所以电子到达 时的速度大小不变,选项D正确。
5. C
【解析】根据做曲线运动的物体所受合力指向轨迹的凹侧,可知该粒子受到的静电力方向与电场方向相反,粒子带负电,选项B错误;粒子到达 点之前静电力做负功,粒子速度减小,电势能增加,粒子经过 点后静电力做正功,粒子速度增大,电势能减少,则粒子在 点速度最小,选项A、D错误;在整个过程中粒子只受静电力,根据牛顿第二定律可知粒子加速度不变,选项C正确。
6. A
7. B
【解析】 的电荷量为 ,粒子飞离偏转电场时的最大侧移为 、 板间距离的一半,则粒子进入与离开偏转电场的两点间的电势差为 ,粒子从进入加速电场到离开偏转电场的过程中,由动能定理得 ,解得 ,选项B正确。
8. B
【解析】因为粒子在电场中做类平抛运动,故 ,根据动能定理,,所以 ,由于 ,, 都相同,但 , 不同,故离开偏转电场时的动能不相同,选项A错误;
粒子做类平抛运动,故在偏转电场中的时间 ,二者都相同,故这个时间相同,选项B正确;
在偏转电场中偏转的角度为 ,则 ,故角度不相同,选项C错误;
在偏转电场中的侧移量 ,也不相同,选项D错误。
9. B
【解析】由于电子带负电,故电子所受电场力方向与场强方向相反,观察图丙知 时刻水平方向负向电压最大,纵向电压为零,故在 方向由 , 方向由 开始扫描,观察乙图知在 时刻 正向电压最大,电子在 这段时间内往 正向偏转, 时刻正向位移最大,故B选项正确。
10. B
【解析】若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向右运动的距离大于向左运动的距离,最终打在 板上,选项A、C错误;若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向左运动的距离大于向右运动的距离,最终打在 板上,选项B正确;若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向左运动的距离小于向右运动的距离,最终打在 板上,选项D错误。
第二部分
11. 加速;偏转;信号;扫描
12. ;
13. (1)Ⅰ;Ⅱ
(2) ;
14. ;
第三部分
15. (1)
【解析】微粒从 点到 点,由动能定理得:
,解得 。
(2)
【解析】微粒通过水平金属板的过程中做匀速直线运动,由匀速运动的位移公式得:,
解得:。
(3)
【解析】为使微粒出射时的动能最大,要求微粒从极板边缘出射,
水平方向:,
竖直方向:,
由牛顿第二定律得:,
解得:。
16.
17. (1)
【解析】设粒子 的质量为 、带电荷量为 ,从 点进入匀强电场时的速度大小为 ,由题意可知,粒子 在 轴右侧匀强电场中做类平抛运动,设从 点运动到 点历时为 ,由类平抛运动规律可得
根据牛顿第二定律有:
联立解得:
在金属板 、 之间,由动能定理有:
联立解得:。
(2) ,其中
【解析】设 、 在右侧电场中运动的加速度分别为 、 , 粒子从 点释放后,竖直向上做初速度为 的匀加速直线运动,经时间 与粒子 相遇,由牛顿运动定律及类平抛运动的规律和几何关系可得,对于 粒子:
对于粒子 :
因为 ,所以粒子 应在第一象限内释放,则有:
联立解得 ,其中
即粒子 释放点的横纵坐标满足的方程为 ,其中 。
第1页(共1 页)
一、单项选择题(共10小题;共40分)
1. 如图()所示的两平行金属板 、 间加上图()所示电压, 时, 板电势比 板高 ,在两板正中央 点放一电子,初速度为零,电子只受静电力而运动,且不会碰到金属板,则这个电子处于 点右侧、速度向右,且速度逐渐减小的时间段是
A. B.
C. D.
2. 如图所示,在真空中有一对带电的平行金属板水平放置。一带电粒子沿平行于板面的方向,从左侧两极板中央射入电场中,恰能从右侧极板边缘处离开电场。不计粒子重力。若可以改变某个量,下列哪种变化,仍能确保粒子一定飞出电场
A. 只增大粒子的带电量 B. 只增大电场强度
C. 只减小粒子的比荷 D. 只减小粒子的入射速度
3. 图 所示为示波管的原理图。如果在电极 之间所加的电压按图 所示的规律变化,在电极 之间所加的电压按图 所示的规律变化,则在荧光屏上会看到的图形是
A. B.
C. D.
4. 如图所示,在 板附近有一电子由静止开始向 板运动,则关于电子到达 时的速率与哪些因素有关的下列解释中正确的是
A. 两极板间的距离越大,加速的时间就越长,则电子获得的速率越大
B. 两极板间的距离越小,加速的时间就越短,则电子获得的速率越小
C. 两极板间的距离越小,加速度就越大,则电子获得的速率越大
D. 与两板间的距离无关,仅与加速电压 有关
5. 如图,一带电粒子以某速度进入水平向右的匀强电场中,在静电力作用下形成图中所示的运动轨迹。 和 是轨迹上的两点,其中 点在轨迹的最右端。不计重力,下列表述正确的是
A. 粒子在 点的速率最大
B. 粒子所受静电力沿电场方向
C. 粒子在电场中的加速度不变
D. 粒子在电场中的电势能始终在增加
6. 示波器是一种电子仪器,可以用它观察电信号随时间变化的情况。示波器的核心部件示波管,由电子枪、偏转电极和荧光屏组成,其原理图如图甲所示。图乙是从右向左看到的荧光屏的平面图。在偏转电极 、 上都不加电压时,电子束将打在荧光屏的中心点;若亮点很快移动,由于视觉暂留关系,能在荧光屏上看到一条亮线,若在 上加如图丙所示的扫描电压,在 上加如图丁所示的信号电压,则在示波管荧光屏上看到的图形是下图中的
A. B.
C. D.
7. 如图所示, 、 两板间加速电压为 , 、 两板间偏转电压为 ,板间距离为 。一个质量为 的粒子()自 板起由静止相继被加速、偏转,飞离偏转电场时的最大侧移为 、 板间距离的一半,则它的出射速度的大小为
A. B. C. D.
8. 如图所示,一价氢离子、一价氦离子和二价氦离子的混合物以相同的初速度沿垂直匀强电场的方向进入同一偏转电场,且经过偏转后都从右侧离开了电场,则三种粒子相同的是
A. 离开偏转电场时的动能 B. 在偏转电场中的时间
C. 在偏转电场中偏转的角度 D. 在偏转电场中的侧移量
9. 如图甲所示为示波管原理图。如果在电极 之间所加的电压按图乙所的规律变化,在电极 之间所加的电压按图丙所示的规律变化,则在荧光屏上会看到的图形是选项中的
A. B.
C. D.
10. 如图甲所示,两平行正对的金属板 、 间加有如图乙所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间 处。若在 时刻释放该粒子,粒子会时而向 板运动,时而向 板运动,并最终打在 板上。则 应满足
A. B. C. D.
二、填空题(共4小题;共24分)
11. 示波管的基本原理:电子在加速电场中被 ,在偏转电场中被 。电子枪的作用是:产生高速飞行的一束电子。偏转电极 上加的是待显示的 电压, 电极上接入仪器自身产生的锯齿形电压,叫做 电压。
12. 电荷量为 、质量为 的正离子 ,电荷量为 、质量为 的正离子 ,均由静止开始经相同电压加速后, 、 动能之比 ,速度大小之比 。
13. 如图是示波管的原理图.它由电子枪、偏转电极( 和 )、荧光屏组成,管内抽成真空.给电子枪通电后,如果在偏转电极 和 上都没有加电压,电子束将打在荧光屏的中心 点.
(1)带电粒子在 区域是加速的,在 区域是偏转的.
(2)若 ,,则粒子向 板偏移,若 ,,则粒子向 板偏移.
14. 如图所示,有一圆心为 ,半径为 的圆, 为圆的直径,在圆形区域所在空间有匀强电场。将质量为 ,电荷量为 的正点电荷由 点静止释放,自圆周上的 点以速率 穿出,已知 与 的夹角 ,运动中点电荷仅受电场力的作用,则匀强电场的场强大小为 ;若将该点电荷从 点移到圆周上的任意一点,则其中点电荷电势能变化的最大值是 。
三、解答题(共3小题;共39分)
15. 如图所示,两组平行带电金属板,一组竖直放置,两板间所加电压为 ,另一组水平放置,板长为 ,两板间的距离为 ,有一个质量为 ,带电荷量为 微粒,从紧靠竖直板上的 点由静止释放后,经 点进入水平金属板并从两板间射出。 点位于两水平金属板的正中间,微粒所受重力忽略不计,求。
(1)该微粒通过 点时的速度大小。
(2)该微粒通过水平金属板的时间。
(3)为使该微粒从两极板射出时的动量最大,加在水平金属板间的电压 应为多大。
16. 如图所示为一示波管的示意图,阴极 和阳极 间加速电压为 ,偏转板 和 间偏转电压为 ,偏转板间距离为 ,板长为 。偏转板中点到荧光屏的距离为 ,从阴极发射出的电子(初速度视为零),经加速和偏转后打在屏上 点,求电子打在屏上的侧移量 。(忽略电子所受重力,不计电子之间的相互作用)
17. 如图所示,带电金属板 、 竖直平行正对放置, 板中心的小孔正好位于平面直角坐标系 的 点, 轴沿竖直方向。在 的区域内存在沿 轴正方向的匀强电场,电场强度大小为 ;比荷为 的带正电的粒子 从 板中心 处由静止释放,其运动轨迹恰好经过 点。粒子 的重力不计。
(1)求金属板 、 之间的电势差 ;
(2)若在粒子 经过 点的同时,在 轴右侧匀强电场中某点由静止释放另一带电粒子 ,使 、 恰能在运动中相碰;假设 的质量是 的 倍,带电情况与 相同,粒子 的重力及 、 之间的相互作用力均忽略不计,求粒子 释放点的横纵坐标 、 应满足的函数关系。
答案
第一部分
1. B
【解析】在 时间内, 板电势比 板高 ,所以电场方向水平向左,电子所受静电力方向向右,加速度方向也向右,所以电子从 点向右做匀加速直线运动,选项A错误;
在 时间内, 板电势比 板低 ,电场强度方向水平向右,所以电子所受静电力方向向左,加速度方向也向左,所以电子向右做匀减速直线运动,当 时速度为零,此时电子在 点的右侧,选项B正确;
在 时间内, 板电势比 板低 ,电场强度方向水平向右,所以电子所受静电力方向向左,加速度方向也向左,所以电子向左做匀加速直线运动,选项C错误;
在 时间内, 板电势比 板高 ,电场强度方向水平向左,所以电子所受静电力方向向右,加速度方向也向右,所以电子向左做匀减速直线运动,到 时刻速度为零,恰好又回到 点,选项D错误。
2. C
【解析】竖直方向偏转距离 ,,,所以 。
增加, 增大,故飞不出,A错误;
增大, 增大,故飞不出,B错误;
减小, 减小,故能飞出,C正确;
减小, 增大,故飞不出,D错误。
3. B
【解析】在 时间内,扫描电压扫描一次,信号电压完成一个周期,当 为正的最大值时,电子打在荧光屏上有正的最大位移,当 为负的最大值时,电子打在荧光屏上有负的最大位移,因此一个周期内荧光屏上的图象为 B 项。
4. D
【解析】由 可知,电子到达 板时的速率与两板间距离无关,仅与加速电压 有关,因电压不变,所以电子到达 时的速度大小不变,选项D正确。
5. C
【解析】根据做曲线运动的物体所受合力指向轨迹的凹侧,可知该粒子受到的静电力方向与电场方向相反,粒子带负电,选项B错误;粒子到达 点之前静电力做负功,粒子速度减小,电势能增加,粒子经过 点后静电力做正功,粒子速度增大,电势能减少,则粒子在 点速度最小,选项A、D错误;在整个过程中粒子只受静电力,根据牛顿第二定律可知粒子加速度不变,选项C正确。
6. A
7. B
【解析】 的电荷量为 ,粒子飞离偏转电场时的最大侧移为 、 板间距离的一半,则粒子进入与离开偏转电场的两点间的电势差为 ,粒子从进入加速电场到离开偏转电场的过程中,由动能定理得 ,解得 ,选项B正确。
8. B
【解析】因为粒子在电场中做类平抛运动,故 ,根据动能定理,,所以 ,由于 ,, 都相同,但 , 不同,故离开偏转电场时的动能不相同,选项A错误;
粒子做类平抛运动,故在偏转电场中的时间 ,二者都相同,故这个时间相同,选项B正确;
在偏转电场中偏转的角度为 ,则 ,故角度不相同,选项C错误;
在偏转电场中的侧移量 ,也不相同,选项D错误。
9. B
【解析】由于电子带负电,故电子所受电场力方向与场强方向相反,观察图丙知 时刻水平方向负向电压最大,纵向电压为零,故在 方向由 , 方向由 开始扫描,观察乙图知在 时刻 正向电压最大,电子在 这段时间内往 正向偏转, 时刻正向位移最大,故B选项正确。
10. B
【解析】若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向右运动的距离大于向左运动的距离,最终打在 板上,选项A、C错误;若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向左运动的距离大于向右运动的距离,最终打在 板上,选项B正确;若 ,带正电粒子先加速向 板运动,再减速运动至速度为零,然后反向加速运动,再减速运动至速度为零,如此往复运动,每次向左运动的距离小于向右运动的距离,最终打在 板上,选项D错误。
第二部分
11. 加速;偏转;信号;扫描
12. ;
13. (1)Ⅰ;Ⅱ
(2) ;
14. ;
第三部分
15. (1)
【解析】微粒从 点到 点,由动能定理得:
,解得 。
(2)
【解析】微粒通过水平金属板的过程中做匀速直线运动,由匀速运动的位移公式得:,
解得:。
(3)
【解析】为使微粒出射时的动能最大,要求微粒从极板边缘出射,
水平方向:,
竖直方向:,
由牛顿第二定律得:,
解得:。
16.
17. (1)
【解析】设粒子 的质量为 、带电荷量为 ,从 点进入匀强电场时的速度大小为 ,由题意可知,粒子 在 轴右侧匀强电场中做类平抛运动,设从 点运动到 点历时为 ,由类平抛运动规律可得
根据牛顿第二定律有:
联立解得:
在金属板 、 之间,由动能定理有:
联立解得:。
(2) ,其中
【解析】设 、 在右侧电场中运动的加速度分别为 、 , 粒子从 点释放后,竖直向上做初速度为 的匀加速直线运动,经时间 与粒子 相遇,由牛顿运动定律及类平抛运动的规律和几何关系可得,对于 粒子:
对于粒子 :
因为 ,所以粒子 应在第一象限内释放,则有:
联立解得 ,其中
即粒子 释放点的横纵坐标满足的方程为 ,其中 。
第1页(共1 页)
