《切线的性质和判定》学案
文档属性
| 名称 | 《切线的性质和判定》学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 125.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-19 00:00:00 | ||
图片预览


文档简介
《圆的切线和性质》练习
一、基础练习
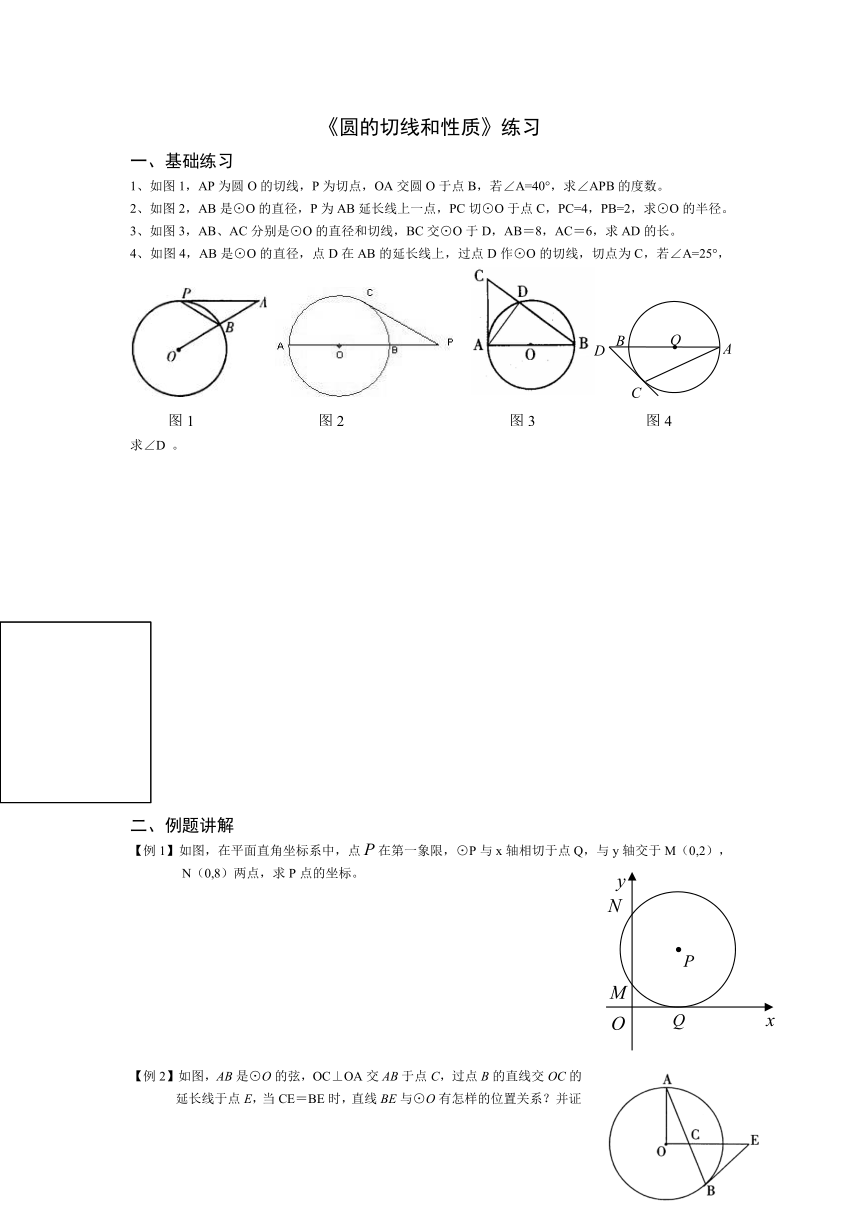
1、如图1,AP为圆O的切线,P为切点,OA交圆O于点B,若∠A=40°,求∠APB的度数。
2、如图2,AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2,求⊙O的半径。
3、如图3,AB、AC分别是⊙O的直径和切线,BC交⊙O于D,AB=8,AC=6,求AD的长。
4、如图4,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,求∠D 。
二、例题讲解
【例1】如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(0,2),
N(0,8)两点,求P点的坐标。
【例2】如图,AB是⊙O的弦,OC⊥OA交AB于点C,过点B的直线交OC的延长线于点E,当CE=BE时,直线BE与⊙O有怎样的位置关系?并证明你的结论.
【例3】如图,AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D,求证:BD是⊙O的切线。
【变形训练】如图,AC是⊙O的直径,点B在AC的处长线上,且BC=OC,点D在圆上,∠BAD=30°,求证:BD是⊙O的切线。
【例4】已知:如图,Rt△ABC中,∠ACB=90°,以AC为直径的半圆O交AB于F,E是BC的中点.求证:直线EF是半圆O的切线.
【例5】如图,在平面直角坐标系中,A、B两点的坐标分别为A(-2,0),B(8,0),以AB为直径的半圆P与y轴交于点M,以AB为一边作正方形ABCD.
①求C、M两点的坐标;
②连接CM,试判断直线CM是否与⊙P相切?说明你的理由;
③在x轴上是否存在一点Q,使得△QMC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
三、巩固练习
1、已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E点,直线EF⊥AC于F.求证:EF与⊙O相切.
2、已知:如图,PA切⊙O于A点,PO∥AC,BC是⊙O的直径.请问:直线PB是否与⊙O相切?说明你的理由.
3、已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.
4、如图,在△ABC中,CA=CB,AB的中点为点D,当⊙D恰与CA相切于E点,求证:BC也是⊙D的切线。
5、如图,A、B在⊙O上,AC是⊙O的切线,∠B=70°,求∠OAB和∠BAC的度数。
6、如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,求AB的长。
7、如图,在RT△ACB中,∠C=90°,AC=3,BC=4,D、E分别是边AB、AC的中点.⊙O过点D,E且与AB相切于点D,求⊙O的半径r.
8、如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.
①求∠AOC的度数;②P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
9、如图,AB是⊙O的直径,AC是弦,过点A的点C有直线互相垂直,垂足为D,且AC平分∠BAD。
求证:CD是⊙O的切线。
10、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
一、基础练习
1、如图1,AP为圆O的切线,P为切点,OA交圆O于点B,若∠A=40°,求∠APB的度数。
2、如图2,AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2,求⊙O的半径。
3、如图3,AB、AC分别是⊙O的直径和切线,BC交⊙O于D,AB=8,AC=6,求AD的长。
4、如图4,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,求∠D 。
二、例题讲解
【例1】如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(0,2),
N(0,8)两点,求P点的坐标。
【例2】如图,AB是⊙O的弦,OC⊥OA交AB于点C,过点B的直线交OC的延长线于点E,当CE=BE时,直线BE与⊙O有怎样的位置关系?并证明你的结论.
【例3】如图,AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D,求证:BD是⊙O的切线。
【变形训练】如图,AC是⊙O的直径,点B在AC的处长线上,且BC=OC,点D在圆上,∠BAD=30°,求证:BD是⊙O的切线。
【例4】已知:如图,Rt△ABC中,∠ACB=90°,以AC为直径的半圆O交AB于F,E是BC的中点.求证:直线EF是半圆O的切线.
【例5】如图,在平面直角坐标系中,A、B两点的坐标分别为A(-2,0),B(8,0),以AB为直径的半圆P与y轴交于点M,以AB为一边作正方形ABCD.
①求C、M两点的坐标;
②连接CM,试判断直线CM是否与⊙P相切?说明你的理由;
③在x轴上是否存在一点Q,使得△QMC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
三、巩固练习
1、已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E点,直线EF⊥AC于F.求证:EF与⊙O相切.
2、已知:如图,PA切⊙O于A点,PO∥AC,BC是⊙O的直径.请问:直线PB是否与⊙O相切?说明你的理由.
3、已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.
4、如图,在△ABC中,CA=CB,AB的中点为点D,当⊙D恰与CA相切于E点,求证:BC也是⊙D的切线。
5、如图,A、B在⊙O上,AC是⊙O的切线,∠B=70°,求∠OAB和∠BAC的度数。
6、如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,求AB的长。
7、如图,在RT△ACB中,∠C=90°,AC=3,BC=4,D、E分别是边AB、AC的中点.⊙O过点D,E且与AB相切于点D,求⊙O的半径r.
8、如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.
①求∠AOC的度数;②P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
9、如图,AB是⊙O的直径,AC是弦,过点A的点C有直线互相垂直,垂足为D,且AC平分∠BAD。
求证:CD是⊙O的切线。
10、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
同课章节目录
