北京课改版九上数学18.7应用举例同步练习 (word版含答案)
文档属性
| 名称 | 北京课改版九上数学18.7应用举例同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 261.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 15:03:15 | ||
图片预览

文档简介
北京课改版九上数学 18.7 应用举例 全练
一、选择题(共2小题;共10分)
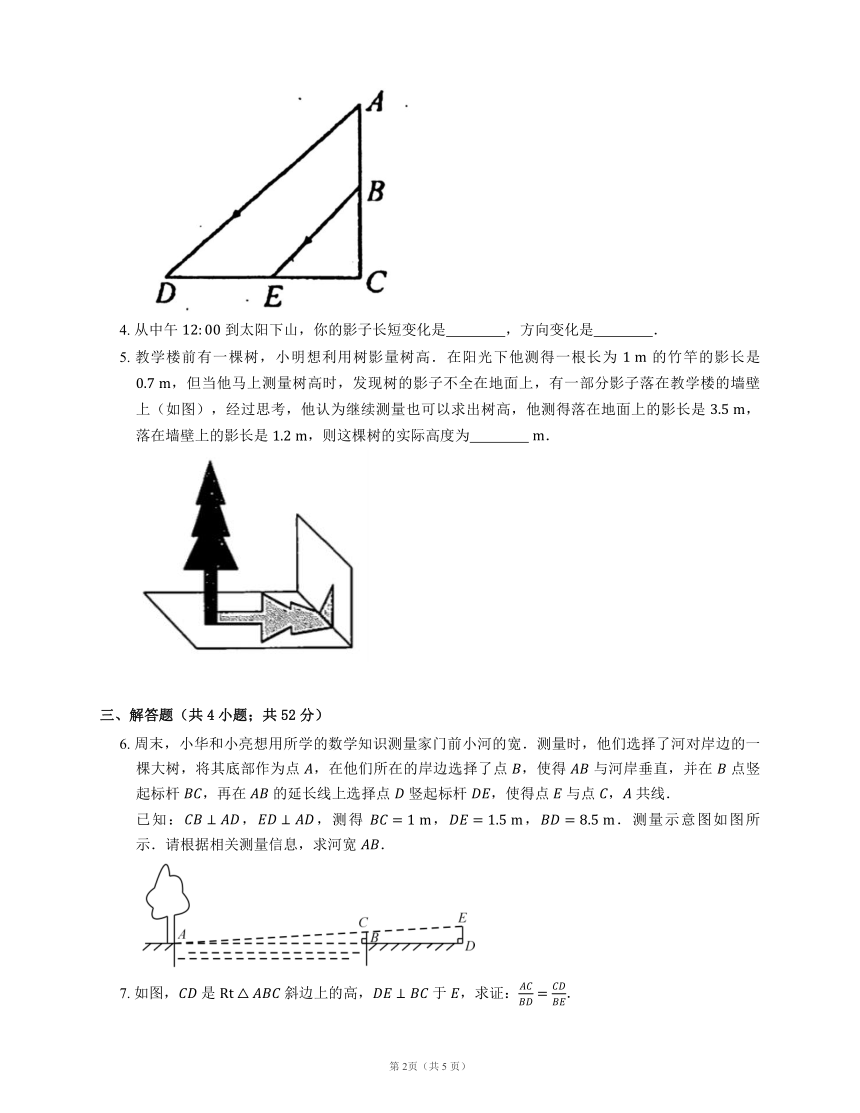
1. 某地需要开辟一条隧道,隧道 的长度无法直接测量.如图所示,在地面上取一点 ,使 到 , 两点均可直接到达,测量找到 和 的中点 ,,测得 的长为 ,则隧道 的长度为
A. B. C. D.
2. 如图,在一块斜边长为 的直角三角形木板( )上截取一个正方形 ,点 在边 上,点 在斜边 上,点 在边 上.若 ,则这块木板截取正方形 后,剩余部分的面积为
A. B. C. D.
二、填空题(共3小题;共15分)
3. 如图,阳光从教室的窗户射入室内,窗户框 在地面上的影长 ,窗户下檐距地面的距离 ,,则窗户的高 .
4. 从中午 到太阳下山,你的影子长短变化是 ,方向变化是 .
5. 教学楼前有一棵树,小明想利用树影量树高.在阳光下他测得一根长为 的竹竿的影长是 ,但当他马上测量树高时,发现树的影子不全在地面上,有一部分影子落在教学楼的墙壁上(如图),经过思考,他认为继续测量也可以求出树高,他测得落在地面上的影长是 ,落在墙壁上的影长是 ,则这棵树的实际高度为 .
三、解答题(共4小题;共52分)
6. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点 ,在他们所在的岸边选择了点 ,使得 与河岸垂直,并在 点竖起标杆 ,再在 的延长线上选择点 竖起标杆 ,使得点 与点 , 共线.
已知:,,测得 ,,.测量示意图如图所示.请根据相关测量信息,求河宽 .
7. 如图, 是 斜边上的高, 于 ,求证:.
8. 为了测量校园内一棵不可攀的树的高度,学校应用实践小组做了如下的探索:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把镜子放在离树() 的点 处,然后沿着直线 后退到点 ,这时恰好在镜子里看到树梢顶点 ,再用皮尺量得 ,观察者眼高 ,请你计算树的高度.
9. 如图所示,已知 是 的边 上一点, 交 于点 ,延长 至点 ,使 ,连接 交 于点 .求证 .
答案
第一部分
1. B
2. A
第二部分
3.
4. 变长,向东
5.
【解析】因为同一时刻树高与影长成比例,
所以 ,
即 ,
所以落在地上的影长对应的树的高度 ,
落在墙壁上的影长对应的树的高度 ,
所以这棵树的实际高度为 .
第三部分
6. ,,
.
,
.
,
,
.
河宽 为 .
7. 由于在直角 中,,,
所以 ,,,
所以 ,.
8. 由题意知 ,
由光的反射原理可知 ,
,即 ,
.
答:树的高度为 .
9. ,
,,
,.
,
,
.
第1页(共1 页)
一、选择题(共2小题;共10分)
1. 某地需要开辟一条隧道,隧道 的长度无法直接测量.如图所示,在地面上取一点 ,使 到 , 两点均可直接到达,测量找到 和 的中点 ,,测得 的长为 ,则隧道 的长度为
A. B. C. D.
2. 如图,在一块斜边长为 的直角三角形木板( )上截取一个正方形 ,点 在边 上,点 在斜边 上,点 在边 上.若 ,则这块木板截取正方形 后,剩余部分的面积为
A. B. C. D.
二、填空题(共3小题;共15分)
3. 如图,阳光从教室的窗户射入室内,窗户框 在地面上的影长 ,窗户下檐距地面的距离 ,,则窗户的高 .
4. 从中午 到太阳下山,你的影子长短变化是 ,方向变化是 .
5. 教学楼前有一棵树,小明想利用树影量树高.在阳光下他测得一根长为 的竹竿的影长是 ,但当他马上测量树高时,发现树的影子不全在地面上,有一部分影子落在教学楼的墙壁上(如图),经过思考,他认为继续测量也可以求出树高,他测得落在地面上的影长是 ,落在墙壁上的影长是 ,则这棵树的实际高度为 .
三、解答题(共4小题;共52分)
6. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点 ,在他们所在的岸边选择了点 ,使得 与河岸垂直,并在 点竖起标杆 ,再在 的延长线上选择点 竖起标杆 ,使得点 与点 , 共线.
已知:,,测得 ,,.测量示意图如图所示.请根据相关测量信息,求河宽 .
7. 如图, 是 斜边上的高, 于 ,求证:.
8. 为了测量校园内一棵不可攀的树的高度,学校应用实践小组做了如下的探索:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把镜子放在离树() 的点 处,然后沿着直线 后退到点 ,这时恰好在镜子里看到树梢顶点 ,再用皮尺量得 ,观察者眼高 ,请你计算树的高度.
9. 如图所示,已知 是 的边 上一点, 交 于点 ,延长 至点 ,使 ,连接 交 于点 .求证 .
答案
第一部分
1. B
2. A
第二部分
3.
4. 变长,向东
5.
【解析】因为同一时刻树高与影长成比例,
所以 ,
即 ,
所以落在地上的影长对应的树的高度 ,
落在墙壁上的影长对应的树的高度 ,
所以这棵树的实际高度为 .
第三部分
6. ,,
.
,
.
,
,
.
河宽 为 .
7. 由于在直角 中,,,
所以 ,,,
所以 ,.
8. 由题意知 ,
由光的反射原理可知 ,
,即 ,
.
答:树的高度为 .
9. ,
,,
,.
,
,
.
第1页(共1 页)
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
