2021-2022学年湖南省张家界市慈利县九年级(上)期末数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年湖南省张家界市慈利县九年级(上)期末数学试卷(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 00:00:00 | ||
图片预览




文档简介
2021-2022学年湖南省张家界市慈利县九年级第一学期期末数学试卷
一、选择题(每小题3分,共8道小题,合计24分)
1.关于反比例函数y=的图象,下列说法正确的是( )
A.点(﹣2,1011)在它的图象上
B.它的图象经过原点
C.它的图象在第一、三象限
D.当x>0时,y随x的增大而增大
2.一元二次方程x2﹣6x﹣1=0配方后可变形为( )
A.(x﹣3)2=8 B.(x﹣3)2=10 C.(x+3)2=8 D.(x+3)2=10
3.已知α、β是一元二次方程2x2﹣2x﹣1=0的两个实数根,则α+β的值为( )
A.﹣1 B.0 C.1 D.2
4.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若,则=( )
A. B. C. D.
5.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③=;④AD BC=DE AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
6.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )
A.45° B.75° C.105° D.120°
7.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.米 B.4sinα米 C.米 D.4cosα米
8.两个反比例函敘和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论其中一定正确的个数是( )
①△ODB的面积不变;②△OCA的面积不变;③△ODB与△OCA的面积相等;④四边形PAOB的面积不会发生变化
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,共16分)
9.如果关于x的一元二次方程ax2+bx﹣1=0的一个解是x=1,则2022﹣a﹣b= .
10.关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为 .
11.已知a:b:c=2:3:4,且a+3b﹣2c=15,则4a﹣3b+c= .
12.某山坡的坡度i=1:3,若沿该山坡前进100m,则升高了 m.
13.如图是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是 米.
14.等腰三角形的腰长为1cm,底边长为cm,则它的底角的正切值为 .
15.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,则sin∠BCD的值是 .
16.如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B,C重合)∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=,有以下的结论:①△BDE∽△CAD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或;④0<BE≤5,其中正确的结论是 (填入正确结论的序号).
三、计算题(本大题共8小题,共60分)
17.计算:sin260°﹣tan30° cos30°+tan45°.
18.已知关于x的一元二次方程x2+(m+3)x+m+2=0.
(1)求证:无论m取何值,原方程总有两个实数根;
(2)若x1,x2是原方程的两根,且x12+x22=2,求m的值.
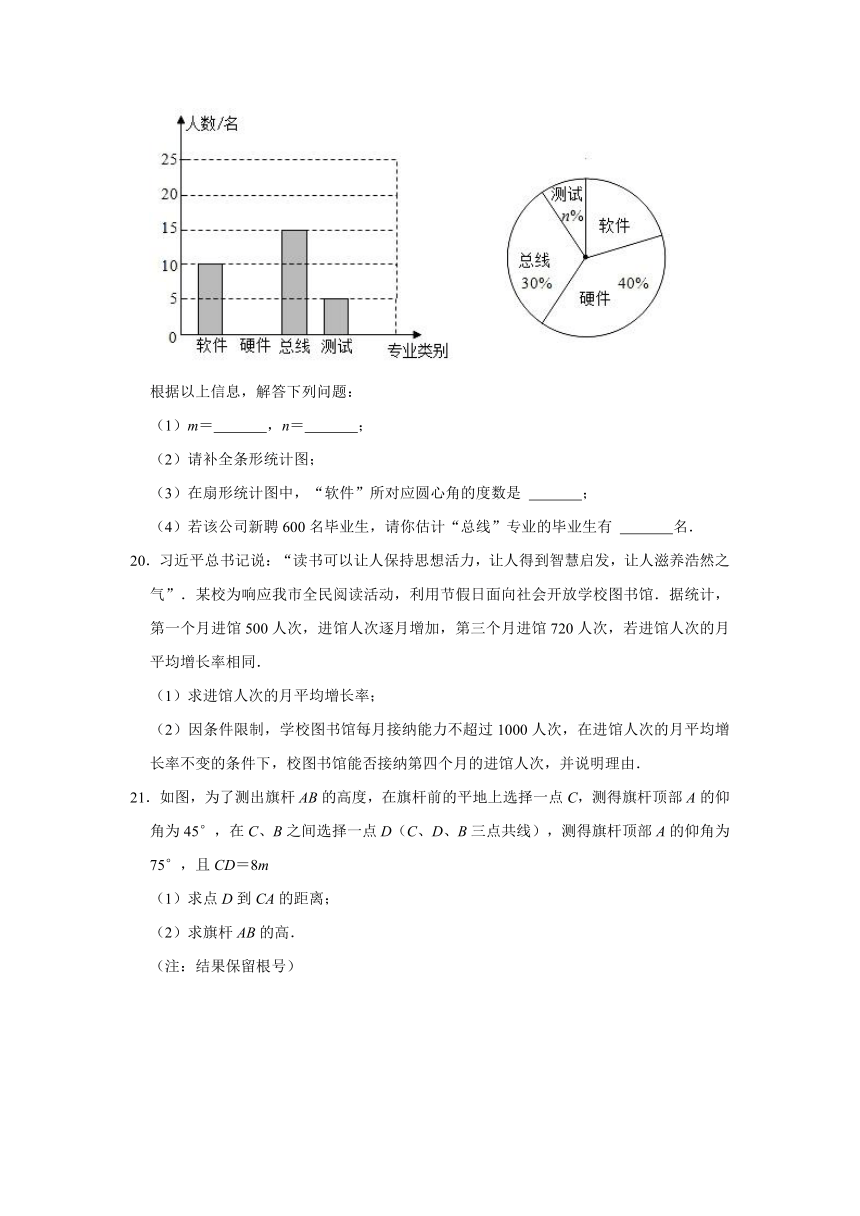
19.以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调查了m名新聘毕业生的专业情况,并将调查结果绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)m= ,n= ;
(2)请补全条形统计图;
(3)在扇形统计图中,“软件”所对应圆心角的度数是 ;
(4)若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有 名.
20.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆500人次,进馆人次逐月增加,第三个月进馆720人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不超过1000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.
21.如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)
22.已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
23.已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,求证:
(1)△AME∽△BAE;
(2)BD2=AD×DM.
24.如图,在矩形ABCD中,AB=3,∠CAB=30°,点P从点A出发,以每秒个单位长度的速度沿AB方向运动,点Q从点C出发,以每秒2个单位长度的速度沿对角线CA方向运动,已知P,Q两点同时出发,当点Q到达点A时,P,Q两点同时停止运动,连接PQ,设运动时间为t秒.
(1)BC= ,AC= .
(2)当t为何值时,△APQ的面积为;
(3)在运动过程中,是否存在一个时刻t,使所得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
(4)当点P关于点Q的对称点P′落在△ACD的内部(不包括边上)时,请求出t的取值范围.(直接写出答案)
参考答案
一、选择题(每小题3分,共8道小题,合计24分)
1.关于反比例函数y=的图象,下列说法正确的是( )
A.点(﹣2,1011)在它的图象上
B.它的图象经过原点
C.它的图象在第一、三象限
D.当x>0时,y随x的增大而增大
【分析】根据反比例函数的性质即可逐一分析找出正确选项.
解:A.当x=﹣2时,y==﹣1011,所以点(﹣2,1011)不在它的图象上,故A说法错误;
B.由反比例函数y=可知,x≠0,所以它的图象不经过原点,故B说法错误;
C.k=2022>0,则图象在第一、三象限,故C说法正确;
D.k=2022>0,图象在一、三象限内,y随x的增大而减小,所以当x>0时,y随x的增大而减小,故D说法错误;
故选:C.
2.一元二次方程x2﹣6x﹣1=0配方后可变形为( )
A.(x﹣3)2=8 B.(x﹣3)2=10 C.(x+3)2=8 D.(x+3)2=10
【分析】根据配方法即可求出答案.
解:∵x2﹣6x﹣1=0,
∴x2﹣6x=1,
∴(x﹣3)2=10,
故选:B.
3.已知α、β是一元二次方程2x2﹣2x﹣1=0的两个实数根,则α+β的值为( )
A.﹣1 B.0 C.1 D.2
【分析】直接利用根与系数的关系求解.
解:∵α、β是一元二次方程2x2﹣2x﹣1=0的两个实数根,
∴α+β=﹣=1.
故选:C.
4.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若,则=( )
A. B. C. D.
【分析】证明△BAC∽△ADC,根据相似三角形的性质列出比例式,得到答案.
解:∵∠BAC=90°,
∴∠B+∠C=90°,
∵AD⊥BC,
∴∠DAC+∠C=90°,
∴∠B=∠DAC,又∠BAC=∠ADC=90°,
∴△BAC∽△ADC,
∴==,
故选:A.
5.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③=;④AD BC=DE AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据相似三角形的判定定理对各条件进行逐一判断即可.
解:①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;
②DE∥BC,则△ADE∽△ABC,故②不符合题意,
③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;
④由AD BC=DE AC可得,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB;
故④不符合题意,
⑤∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故⑤符合题意;
故选:C.
6.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )
A.45° B.75° C.105° D.120°
【分析】根据非负数的性质列出关系式,根据特殊角的三角函数值求出∠A、∠B的度数,根据三角形内角和定理计算即可.
解:由题意得,sinA﹣=0,﹣cosB=0,
即sinA=,=cosB,
解得,∠A=30°,∠B=45°,
∴∠C=180°﹣∠A﹣∠B=105°,
故选:C.
7.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.米 B.4sinα米 C.米 D.4cosα米
【分析】过点A′作A′C⊥AB于点C,根据锐角三角函数的定义即可求出答案.
解:过点A′作A′C⊥AB于点C,
由题意可知:A′O=AO=4,
∴sinα=,
∴A′C=4sinα,
故选:B.
8.两个反比例函敘和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论其中一定正确的个数是( )
①△ODB的面积不变;②△OCA的面积不变;③△ODB与△OCA的面积相等;④四边形PAOB的面积不会发生变化
A.1 B.2 C.3 D.4
【分析】由反比例函数比例系数k的几何意义判断各结论即可.
解:由题意可得,△ODB的面积=,△OCA的面积=,矩形CODP的面积=2,
∴△ODB的面积=△OCA的面积,
∴四边形PAOB的面积=矩形CODP的面积﹣△ODB的面积﹣△OCA的面积=2﹣﹣=1,
∴①②③④均正确.
故选:D.
二、填空题(本大题共8小题,共16分)
9.如果关于x的一元二次方程ax2+bx﹣1=0的一个解是x=1,则2022﹣a﹣b= 2021 .
【分析】利用一元二次方程解的定义得到a+b=1,然后把2022﹣a﹣b变形为2022﹣(a+b),再利用整体代入的方法计算.
解:把x=1代入方程ax2+bx﹣1=0得a+b﹣1=0,
所以a+b=1,
所以2022﹣a﹣b=2022﹣(a+b)=2022﹣1=2021.
故答案为:2021.
10.关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为 ﹣1 .
【分析】已知了一元二次方程的一个实数根,可将其代入该方程中,即可求出a的值.
解:∵关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,
∴|a|﹣1=0,
即a=±1,
∵a﹣1≠0
∴a=﹣1,
故答案为:﹣1.
11.已知a:b:c=2:3:4,且a+3b﹣2c=15,则4a﹣3b+c= 15 .
【分析】设a=2k,b=3k,c=4k,代入求出k,即可求出答案;把a、b、c的值代入,求出即可.
解:(1)设a=2k,b=3k,c=4k,
∵a+3b﹣2c=15,
∴2k+9k﹣8k=15,
∴k=5,
∴a=10,b=15,c=20;
∵a=10,b=15,c=20,
∴4a﹣3b+c
=4×10﹣3×15+20
=15.
故答案为:15.
12.某山坡的坡度i=1:3,若沿该山坡前进100m,则升高了 m.
【分析】根据题意作出图形,可得BC:AB=1:3,设BC=x,AB=3x,根据勾股定理求出AC,然后根据AC=100m,求出x的值.
解:某山坡的坡度i=1:3,若沿该山坡前进100m,设BC=x,AB=3x,
则AC==x=100,
解得:x=10,
则升高了10m.
故答案为:10.
13.如图是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是 8 米.
【分析】由光学知识反射角等于入射角不难分析得出∠APB=∠CPD,再由∠ABP=∠CDP=90°得到△ABP∽△CDP,得到=代入数值求的CD=8.
解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=即=
解得:CD=8米.
14.等腰三角形的腰长为1cm,底边长为cm,则它的底角的正切值为 .
【分析】作等腰三角形底边上的高,将问题转化到直角三角形中,求底角的正切值即可.
解:设AB=AC=1,BC=,
过A点作AD⊥BC,垂足为D,如图所示:
则BD=BC=,
在Rt△ABD中,由勾股定理得:AD===,
∴tanB===,
故答案为:.
15.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,则sin∠BCD的值是 .
【分析】先利用勾股定理求出AB,再利用同角的余角相等说明∠BCD与∠A的关系,最后利用∠A的正弦得结论.
解:在Rt△ABC中,
∵∠ACB=90°,AC=4,BC=3,
∴AB=5.
∵∠A+∠B=90°,∠B+∠BCD=90°,
∴∠A=∠BCD.
∴sin∠BCD=sinA==.
故答案为:.
16.如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B,C重合)∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=,有以下的结论:①△BDE∽△CAD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或;④0<BE≤5,其中正确的结论是 ①②③ (填入正确结论的序号).
【分析】①根据有两组对应角相等的三角形相似即可证明;
②由CD=9,则BD=15,然后根据有两组对应角相等且夹边也相等的三角形全等,即可证得;
③分两种情况讨论,通过三角形相似即可求得;
④依据相似三角形对应边成比例即可求得.
解:①∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B,
∴∠ADC=180°﹣α﹣∠BDE,
∵∠BED=180°﹣α﹣∠BDE,
∴∠BED=∠ADC,
∴△BDE∽△CAD;
故①正确;
②作AG⊥BC于G,
∵∠ADE=∠B=α,tan∠α=,
∴,
∴,
∴cosα=,
∵AB=AC=15,
∴BG=12,
∴BC=24,
∵CD=9,
∴BD=15,
∴AC=BD.
∵∠ADE+∠BDE=∠C+∠DAC,∠ADE=∠C=α,
∴∠EDB=∠DAC,
在△ACD与△DBE中,
,
∴△ACD≌△BDE(ASA).
故②正确;
③当∠BED=90°时,由①可知:△ADE∽△ABD,
∴∠ADB=∠AED,
∵∠BED=90°,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴∠ADE=∠B=α,
∵tan∠α=,AB=15,
∴,
∴BD=12.
当∠BDE=90°时,△BDE∽△CAD,
∵∠BDE=90°,
∴∠CAD=90°,
∵∠C=α且cosα=,AC=15,
∴cosC=,
∴CD=.
∵BC=24,
∴BD=24﹣=,
即当△DCE为直角三角形时,BD=12或.
故③正确;
④易证得△BDE∽△CAD,由②可知BC=24,
设CD=y,BE=x,
∴,
∴,
整理得:y2﹣24y+144=144﹣15x,
即(y﹣12)2=144﹣15x,
∴0<x≤,
∴0<BE≤.
故④错误.
故正确的结论为:①②③.
故答案为:①②③.
三、计算题(本大题共8小题,共60分)
17.计算:sin260°﹣tan30° cos30°+tan45°.
【分析】根据特殊角的三角函数值,可得sin60°、tan30°、cos30°、tan45°的值,代入原式可得答案.
解:原式=()2﹣×+1
=.
18.已知关于x的一元二次方程x2+(m+3)x+m+2=0.
(1)求证:无论m取何值,原方程总有两个实数根;
(2)若x1,x2是原方程的两根,且x12+x22=2,求m的值.
【分析】(1)根据根的判别式即可求出答案.
解:(1)证明:∵Δ=(m+3)2﹣4(m+2)
=(m+1)2,
∵无论m取何值,(m+1)2≥0,
∴原方程总有两个实数根.
(2)∵x1,x2是原方程的两根,
∴x1+x2=﹣(m+3),x1x2=m+2,
∵x12+x22=2,
∴(x1+x2)2﹣2x1x2=2,
∴代入化简可得:m2+4m+3=0,
解得:m=﹣3或m=﹣1
19.以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调查了m名新聘毕业生的专业情况,并将调查结果绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)m= 50 ,n= 10 ;
(2)请补全条形统计图;
(3)在扇形统计图中,“软件”所对应圆心角的度数是 72° ;
(4)若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有 180 名.
【分析】(1)根据总线的人数和所占的百分比,可以求得m的值,然后即可计算出n的值;
(2)根据(1)中的结果和硬件所占的百分比,可以求得硬件专业的毕业生,从而可以将条形统计图补充完整;
(3)根据条形统计图中的数据,可以计算出在扇形统计图中,“软件”所对应的扇形的圆心角的度数;
(4)根据统计图中的数据,可以计算出“总线”专业的毕业生的人数.
解:(1)m=15÷30%=50,
n%=5÷50×100%=10%,
故答案为:50,10;
(2)补全的条形统计图如图所示;
(3)在扇形统计图中,“软件”所对应的扇形的圆心角是360°×=72°,
故答案为:72°;
(4)估计“总线”专业的毕业生有:600×30%=180(名),
故答案为:180.
20.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆500人次,进馆人次逐月增加,第三个月进馆720人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不超过1000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.
【分析】(1)设进馆人次的月平均增长率是x,根据第一个月及第三个月的进馆人次数,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)根据第四个月的进馆人次数=第三个月的进馆人次数×(1+增长率),可求出第四个月的进馆人次数,再与1000进行比较后即可得出结论.
解:(1)设进馆人次的月平均增长率是x,
依题意,得:500(1+x)2=720,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:进馆人次的月平均增长率是20%.
(2)能,理由如下:
720(1+20%)=864(人次),864<1000,
∴能够接纳.
答:校图书馆能接纳第四个月的进馆人次.
21.如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)
【分析】(1)作DE⊥AC于点E,根据sinC=即可得DE;
(2)由∠C=45°可得CE,由tan∠EAD=可得AE,即可得AC的长,再在Rt△ABC中,根据sinC=即可得AB的长.
解:(1)如图,作DE⊥AC于点E,
再Rt△CDE中,sinC=,
∴=,
∴DE=4,
答:点D到CA的距离为4 m;
(2)在Rt△CDE中,∠C=45°,
∴△CDE为等腰直角三角形,
∴CE=DE=4,
∵∠ADB=75°,∠C=45°,
∴∠EAD=∠ADB﹣∠C=30°,
∴在Rt△ADE中,tan∠EAD=,
∴=,
∴AE=4,
∴AC=AE+CE=4+4,
在Rt△ABC中,sinC=,
∴=,
∴AB=4+4,
答:旗杆AB的高为(4+4)m.
22.已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
【分析】(1)先把点A的坐标代入反比例函数解析式,即可得到m=﹣8,再把点B的坐标代入反比例函数解析式,即可求出n=2,然后利用待定系数法确定一次函数的解析式;
(2)先求出直线y=﹣x﹣2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;
(3)观察函数图象得到当x<﹣4或0<x<2时,一次函数的图象在反比例函数图象上方,据此可得不等式的解集.
解:(1)把A(﹣4,2)代入y=,得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣,
把B(n,﹣4)代入y=﹣,得﹣4n=﹣8,
解得n=2,
把A(﹣4,2)和B(2,﹣4)代入y=kx+b,得
,
解得,
所以一次函数的解析式为y=﹣x﹣2;
(2)y=﹣x﹣2中,令y=0,则x=﹣2,
即直线y=﹣x﹣2与x轴交于点C(﹣2,0),
∴S△AOB=S△AOC+S△BOC=×2×2+×2×4=6;
(3)由图可得,不等式kx+b﹣>0的解集为:x<﹣4或0<x<2.
23.已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,求证:
(1)△AME∽△BAE;
(2)BD2=AD×DM.
【分析】(1)根据等边三角形的性质可得出AB=BC、∠ABD=∠C,结合BD=CE即可证出△ABD≌△BCE(SAS),根据全等三角形的性质可得出∠CBE=∠BAD,通过角的计算可得出∠EAM=∠EBA,再结合∠AEM=∠BEA即可证出△AME∽△BAE;
(2)根据相似三角形的性质可得出∠AME=∠BAE=60°,由对顶角相等可得出∠BMD=60°,再结合∠ABD=60°、∠BDM=∠ADB,即可证出△ABD∽△BMD,根据相似三角形的性质可证出BD2=AD×DM.
【解答】证明:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°.
在△ABD和△BCE中,,
∴△ABD≌△BCE(SAS),
∴∠CBE=∠BAD,
∴∠EAM=∠EBA.
又∵∠AEM=∠BEA,
∴△AME∽△BAE.
(2)∵△AME∽△BAE,
∴∠AME=∠BAE=60°,
∴∠BMD=60°.
又∵∠ABD=60°,∠BDM=∠ADB,
∴△ABD∽△BMD,
∴BD2=AD×DM.
24.如图,在矩形ABCD中,AB=3,∠CAB=30°,点P从点A出发,以每秒个单位长度的速度沿AB方向运动,点Q从点C出发,以每秒2个单位长度的速度沿对角线CA方向运动,已知P,Q两点同时出发,当点Q到达点A时,P,Q两点同时停止运动,连接PQ,设运动时间为t秒.
(1)BC= 3 ,AC= 6 .
(2)当t为何值时,△APQ的面积为;
(3)在运动过程中,是否存在一个时刻t,使所得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
(4)当点P关于点Q的对称点P′落在△ACD的内部(不包括边上)时,请求出t的取值范围.(直接写出答案)
【分析】(1)根据矩形的性质和含30°角的直角三角形的性质解答即可;
(2)根据直角三角形的性质和三角形的面积公式解答即可;
(3)分三种情况,利用翻折的性质解答即可;
(4)根据对称的性质解答即可.
【解答】(1)解:∵矩形ABCD,AB=3,∠CAB=30°,
∴BC=3,AC=6;
故答案为:3;6;
(2)解:过点Q作QH⊥AB,垂足为H,
由题意知,AP=t,AQ=6﹣2t,
在Rt△AQH中,∠QAP=30°,
∴QH=AQ=3﹣t,
∴,
解得:t1=1,t2=2;
(3)解:①当沿PQ翻折时,则AP=AQ,则,
解得:t=,
②当沿AP翻折时,则AQ=QP,过点Q作QM⊥AB,垂足为M,
则AM=AP=t,
在Rt△AQM中,∠QAM=30°,
∴,
解得:t=2,
③当沿AQ翻折时,则AP=PQ,
过点P作PM⊥AC,垂足为M,
则AM=AQ=3﹣t,
在Rt△AMP中,∠PAM=30°,
∴3﹣t=,
解得:t=,
综上所述,t的值为12﹣6或2或;
(4)由题意知,AP=t,AQ=6﹣2t,
∴P'在△ACD中,满足,
∴1.5<t<2.
一、选择题(每小题3分,共8道小题,合计24分)
1.关于反比例函数y=的图象,下列说法正确的是( )
A.点(﹣2,1011)在它的图象上
B.它的图象经过原点
C.它的图象在第一、三象限
D.当x>0时,y随x的增大而增大
2.一元二次方程x2﹣6x﹣1=0配方后可变形为( )
A.(x﹣3)2=8 B.(x﹣3)2=10 C.(x+3)2=8 D.(x+3)2=10
3.已知α、β是一元二次方程2x2﹣2x﹣1=0的两个实数根,则α+β的值为( )
A.﹣1 B.0 C.1 D.2
4.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若,则=( )
A. B. C. D.
5.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③=;④AD BC=DE AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
6.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )
A.45° B.75° C.105° D.120°
7.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.米 B.4sinα米 C.米 D.4cosα米
8.两个反比例函敘和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论其中一定正确的个数是( )
①△ODB的面积不变;②△OCA的面积不变;③△ODB与△OCA的面积相等;④四边形PAOB的面积不会发生变化
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,共16分)
9.如果关于x的一元二次方程ax2+bx﹣1=0的一个解是x=1,则2022﹣a﹣b= .
10.关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为 .
11.已知a:b:c=2:3:4,且a+3b﹣2c=15,则4a﹣3b+c= .
12.某山坡的坡度i=1:3,若沿该山坡前进100m,则升高了 m.
13.如图是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是 米.
14.等腰三角形的腰长为1cm,底边长为cm,则它的底角的正切值为 .
15.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,则sin∠BCD的值是 .
16.如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B,C重合)∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=,有以下的结论:①△BDE∽△CAD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或;④0<BE≤5,其中正确的结论是 (填入正确结论的序号).
三、计算题(本大题共8小题,共60分)
17.计算:sin260°﹣tan30° cos30°+tan45°.
18.已知关于x的一元二次方程x2+(m+3)x+m+2=0.
(1)求证:无论m取何值,原方程总有两个实数根;
(2)若x1,x2是原方程的两根,且x12+x22=2,求m的值.
19.以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调查了m名新聘毕业生的专业情况,并将调查结果绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)m= ,n= ;
(2)请补全条形统计图;
(3)在扇形统计图中,“软件”所对应圆心角的度数是 ;
(4)若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有 名.
20.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆500人次,进馆人次逐月增加,第三个月进馆720人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不超过1000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.
21.如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)
22.已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
23.已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,求证:
(1)△AME∽△BAE;
(2)BD2=AD×DM.
24.如图,在矩形ABCD中,AB=3,∠CAB=30°,点P从点A出发,以每秒个单位长度的速度沿AB方向运动,点Q从点C出发,以每秒2个单位长度的速度沿对角线CA方向运动,已知P,Q两点同时出发,当点Q到达点A时,P,Q两点同时停止运动,连接PQ,设运动时间为t秒.
(1)BC= ,AC= .
(2)当t为何值时,△APQ的面积为;
(3)在运动过程中,是否存在一个时刻t,使所得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
(4)当点P关于点Q的对称点P′落在△ACD的内部(不包括边上)时,请求出t的取值范围.(直接写出答案)
参考答案
一、选择题(每小题3分,共8道小题,合计24分)
1.关于反比例函数y=的图象,下列说法正确的是( )
A.点(﹣2,1011)在它的图象上
B.它的图象经过原点
C.它的图象在第一、三象限
D.当x>0时,y随x的增大而增大
【分析】根据反比例函数的性质即可逐一分析找出正确选项.
解:A.当x=﹣2时,y==﹣1011,所以点(﹣2,1011)不在它的图象上,故A说法错误;
B.由反比例函数y=可知,x≠0,所以它的图象不经过原点,故B说法错误;
C.k=2022>0,则图象在第一、三象限,故C说法正确;
D.k=2022>0,图象在一、三象限内,y随x的增大而减小,所以当x>0时,y随x的增大而减小,故D说法错误;
故选:C.
2.一元二次方程x2﹣6x﹣1=0配方后可变形为( )
A.(x﹣3)2=8 B.(x﹣3)2=10 C.(x+3)2=8 D.(x+3)2=10
【分析】根据配方法即可求出答案.
解:∵x2﹣6x﹣1=0,
∴x2﹣6x=1,
∴(x﹣3)2=10,
故选:B.
3.已知α、β是一元二次方程2x2﹣2x﹣1=0的两个实数根,则α+β的值为( )
A.﹣1 B.0 C.1 D.2
【分析】直接利用根与系数的关系求解.
解:∵α、β是一元二次方程2x2﹣2x﹣1=0的两个实数根,
∴α+β=﹣=1.
故选:C.
4.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若,则=( )
A. B. C. D.
【分析】证明△BAC∽△ADC,根据相似三角形的性质列出比例式,得到答案.
解:∵∠BAC=90°,
∴∠B+∠C=90°,
∵AD⊥BC,
∴∠DAC+∠C=90°,
∴∠B=∠DAC,又∠BAC=∠ADC=90°,
∴△BAC∽△ADC,
∴==,
故选:A.
5.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③=;④AD BC=DE AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据相似三角形的判定定理对各条件进行逐一判断即可.
解:①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;
②DE∥BC,则△ADE∽△ABC,故②不符合题意,
③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;
④由AD BC=DE AC可得,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB;
故④不符合题意,
⑤∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故⑤符合题意;
故选:C.
6.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )
A.45° B.75° C.105° D.120°
【分析】根据非负数的性质列出关系式,根据特殊角的三角函数值求出∠A、∠B的度数,根据三角形内角和定理计算即可.
解:由题意得,sinA﹣=0,﹣cosB=0,
即sinA=,=cosB,
解得,∠A=30°,∠B=45°,
∴∠C=180°﹣∠A﹣∠B=105°,
故选:C.
7.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.米 B.4sinα米 C.米 D.4cosα米
【分析】过点A′作A′C⊥AB于点C,根据锐角三角函数的定义即可求出答案.
解:过点A′作A′C⊥AB于点C,
由题意可知:A′O=AO=4,
∴sinα=,
∴A′C=4sinα,
故选:B.
8.两个反比例函敘和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论其中一定正确的个数是( )
①△ODB的面积不变;②△OCA的面积不变;③△ODB与△OCA的面积相等;④四边形PAOB的面积不会发生变化
A.1 B.2 C.3 D.4
【分析】由反比例函数比例系数k的几何意义判断各结论即可.
解:由题意可得,△ODB的面积=,△OCA的面积=,矩形CODP的面积=2,
∴△ODB的面积=△OCA的面积,
∴四边形PAOB的面积=矩形CODP的面积﹣△ODB的面积﹣△OCA的面积=2﹣﹣=1,
∴①②③④均正确.
故选:D.
二、填空题(本大题共8小题,共16分)
9.如果关于x的一元二次方程ax2+bx﹣1=0的一个解是x=1,则2022﹣a﹣b= 2021 .
【分析】利用一元二次方程解的定义得到a+b=1,然后把2022﹣a﹣b变形为2022﹣(a+b),再利用整体代入的方法计算.
解:把x=1代入方程ax2+bx﹣1=0得a+b﹣1=0,
所以a+b=1,
所以2022﹣a﹣b=2022﹣(a+b)=2022﹣1=2021.
故答案为:2021.
10.关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为 ﹣1 .
【分析】已知了一元二次方程的一个实数根,可将其代入该方程中,即可求出a的值.
解:∵关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,
∴|a|﹣1=0,
即a=±1,
∵a﹣1≠0
∴a=﹣1,
故答案为:﹣1.
11.已知a:b:c=2:3:4,且a+3b﹣2c=15,则4a﹣3b+c= 15 .
【分析】设a=2k,b=3k,c=4k,代入求出k,即可求出答案;把a、b、c的值代入,求出即可.
解:(1)设a=2k,b=3k,c=4k,
∵a+3b﹣2c=15,
∴2k+9k﹣8k=15,
∴k=5,
∴a=10,b=15,c=20;
∵a=10,b=15,c=20,
∴4a﹣3b+c
=4×10﹣3×15+20
=15.
故答案为:15.
12.某山坡的坡度i=1:3,若沿该山坡前进100m,则升高了 m.
【分析】根据题意作出图形,可得BC:AB=1:3,设BC=x,AB=3x,根据勾股定理求出AC,然后根据AC=100m,求出x的值.
解:某山坡的坡度i=1:3,若沿该山坡前进100m,设BC=x,AB=3x,
则AC==x=100,
解得:x=10,
则升高了10m.
故答案为:10.
13.如图是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.4米,BP=2.1米,PD=12米.那么该古城墙CD的高度是 8 米.
【分析】由光学知识反射角等于入射角不难分析得出∠APB=∠CPD,再由∠ABP=∠CDP=90°得到△ABP∽△CDP,得到=代入数值求的CD=8.
解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=即=
解得:CD=8米.
14.等腰三角形的腰长为1cm,底边长为cm,则它的底角的正切值为 .
【分析】作等腰三角形底边上的高,将问题转化到直角三角形中,求底角的正切值即可.
解:设AB=AC=1,BC=,
过A点作AD⊥BC,垂足为D,如图所示:
则BD=BC=,
在Rt△ABD中,由勾股定理得:AD===,
∴tanB===,
故答案为:.
15.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,则sin∠BCD的值是 .
【分析】先利用勾股定理求出AB,再利用同角的余角相等说明∠BCD与∠A的关系,最后利用∠A的正弦得结论.
解:在Rt△ABC中,
∵∠ACB=90°,AC=4,BC=3,
∴AB=5.
∵∠A+∠B=90°,∠B+∠BCD=90°,
∴∠A=∠BCD.
∴sin∠BCD=sinA==.
故答案为:.
16.如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B,C重合)∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=,有以下的结论:①△BDE∽△CAD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或;④0<BE≤5,其中正确的结论是 ①②③ (填入正确结论的序号).
【分析】①根据有两组对应角相等的三角形相似即可证明;
②由CD=9,则BD=15,然后根据有两组对应角相等且夹边也相等的三角形全等,即可证得;
③分两种情况讨论,通过三角形相似即可求得;
④依据相似三角形对应边成比例即可求得.
解:①∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B,
∴∠ADC=180°﹣α﹣∠BDE,
∵∠BED=180°﹣α﹣∠BDE,
∴∠BED=∠ADC,
∴△BDE∽△CAD;
故①正确;
②作AG⊥BC于G,
∵∠ADE=∠B=α,tan∠α=,
∴,
∴,
∴cosα=,
∵AB=AC=15,
∴BG=12,
∴BC=24,
∵CD=9,
∴BD=15,
∴AC=BD.
∵∠ADE+∠BDE=∠C+∠DAC,∠ADE=∠C=α,
∴∠EDB=∠DAC,
在△ACD与△DBE中,
,
∴△ACD≌△BDE(ASA).
故②正确;
③当∠BED=90°时,由①可知:△ADE∽△ABD,
∴∠ADB=∠AED,
∵∠BED=90°,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴∠ADE=∠B=α,
∵tan∠α=,AB=15,
∴,
∴BD=12.
当∠BDE=90°时,△BDE∽△CAD,
∵∠BDE=90°,
∴∠CAD=90°,
∵∠C=α且cosα=,AC=15,
∴cosC=,
∴CD=.
∵BC=24,
∴BD=24﹣=,
即当△DCE为直角三角形时,BD=12或.
故③正确;
④易证得△BDE∽△CAD,由②可知BC=24,
设CD=y,BE=x,
∴,
∴,
整理得:y2﹣24y+144=144﹣15x,
即(y﹣12)2=144﹣15x,
∴0<x≤,
∴0<BE≤.
故④错误.
故正确的结论为:①②③.
故答案为:①②③.
三、计算题(本大题共8小题,共60分)
17.计算:sin260°﹣tan30° cos30°+tan45°.
【分析】根据特殊角的三角函数值,可得sin60°、tan30°、cos30°、tan45°的值,代入原式可得答案.
解:原式=()2﹣×+1
=.
18.已知关于x的一元二次方程x2+(m+3)x+m+2=0.
(1)求证:无论m取何值,原方程总有两个实数根;
(2)若x1,x2是原方程的两根,且x12+x22=2,求m的值.
【分析】(1)根据根的判别式即可求出答案.
解:(1)证明:∵Δ=(m+3)2﹣4(m+2)
=(m+1)2,
∵无论m取何值,(m+1)2≥0,
∴原方程总有两个实数根.
(2)∵x1,x2是原方程的两根,
∴x1+x2=﹣(m+3),x1x2=m+2,
∵x12+x22=2,
∴(x1+x2)2﹣2x1x2=2,
∴代入化简可得:m2+4m+3=0,
解得:m=﹣3或m=﹣1
19.以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调查了m名新聘毕业生的专业情况,并将调查结果绘制成两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)m= 50 ,n= 10 ;
(2)请补全条形统计图;
(3)在扇形统计图中,“软件”所对应圆心角的度数是 72° ;
(4)若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有 180 名.
【分析】(1)根据总线的人数和所占的百分比,可以求得m的值,然后即可计算出n的值;
(2)根据(1)中的结果和硬件所占的百分比,可以求得硬件专业的毕业生,从而可以将条形统计图补充完整;
(3)根据条形统计图中的数据,可以计算出在扇形统计图中,“软件”所对应的扇形的圆心角的度数;
(4)根据统计图中的数据,可以计算出“总线”专业的毕业生的人数.
解:(1)m=15÷30%=50,
n%=5÷50×100%=10%,
故答案为:50,10;
(2)补全的条形统计图如图所示;
(3)在扇形统计图中,“软件”所对应的扇形的圆心角是360°×=72°,
故答案为:72°;
(4)估计“总线”专业的毕业生有:600×30%=180(名),
故答案为:180.
20.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆500人次,进馆人次逐月增加,第三个月进馆720人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不超过1000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.
【分析】(1)设进馆人次的月平均增长率是x,根据第一个月及第三个月的进馆人次数,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)根据第四个月的进馆人次数=第三个月的进馆人次数×(1+增长率),可求出第四个月的进馆人次数,再与1000进行比较后即可得出结论.
解:(1)设进馆人次的月平均增长率是x,
依题意,得:500(1+x)2=720,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:进馆人次的月平均增长率是20%.
(2)能,理由如下:
720(1+20%)=864(人次),864<1000,
∴能够接纳.
答:校图书馆能接纳第四个月的进馆人次.
21.如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)
【分析】(1)作DE⊥AC于点E,根据sinC=即可得DE;
(2)由∠C=45°可得CE,由tan∠EAD=可得AE,即可得AC的长,再在Rt△ABC中,根据sinC=即可得AB的长.
解:(1)如图,作DE⊥AC于点E,
再Rt△CDE中,sinC=,
∴=,
∴DE=4,
答:点D到CA的距离为4 m;
(2)在Rt△CDE中,∠C=45°,
∴△CDE为等腰直角三角形,
∴CE=DE=4,
∵∠ADB=75°,∠C=45°,
∴∠EAD=∠ADB﹣∠C=30°,
∴在Rt△ADE中,tan∠EAD=,
∴=,
∴AE=4,
∴AC=AE+CE=4+4,
在Rt△ABC中,sinC=,
∴=,
∴AB=4+4,
答:旗杆AB的高为(4+4)m.
22.已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
【分析】(1)先把点A的坐标代入反比例函数解析式,即可得到m=﹣8,再把点B的坐标代入反比例函数解析式,即可求出n=2,然后利用待定系数法确定一次函数的解析式;
(2)先求出直线y=﹣x﹣2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;
(3)观察函数图象得到当x<﹣4或0<x<2时,一次函数的图象在反比例函数图象上方,据此可得不等式的解集.
解:(1)把A(﹣4,2)代入y=,得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣,
把B(n,﹣4)代入y=﹣,得﹣4n=﹣8,
解得n=2,
把A(﹣4,2)和B(2,﹣4)代入y=kx+b,得
,
解得,
所以一次函数的解析式为y=﹣x﹣2;
(2)y=﹣x﹣2中,令y=0,则x=﹣2,
即直线y=﹣x﹣2与x轴交于点C(﹣2,0),
∴S△AOB=S△AOC+S△BOC=×2×2+×2×4=6;
(3)由图可得,不等式kx+b﹣>0的解集为:x<﹣4或0<x<2.
23.已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,求证:
(1)△AME∽△BAE;
(2)BD2=AD×DM.
【分析】(1)根据等边三角形的性质可得出AB=BC、∠ABD=∠C,结合BD=CE即可证出△ABD≌△BCE(SAS),根据全等三角形的性质可得出∠CBE=∠BAD,通过角的计算可得出∠EAM=∠EBA,再结合∠AEM=∠BEA即可证出△AME∽△BAE;
(2)根据相似三角形的性质可得出∠AME=∠BAE=60°,由对顶角相等可得出∠BMD=60°,再结合∠ABD=60°、∠BDM=∠ADB,即可证出△ABD∽△BMD,根据相似三角形的性质可证出BD2=AD×DM.
【解答】证明:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°.
在△ABD和△BCE中,,
∴△ABD≌△BCE(SAS),
∴∠CBE=∠BAD,
∴∠EAM=∠EBA.
又∵∠AEM=∠BEA,
∴△AME∽△BAE.
(2)∵△AME∽△BAE,
∴∠AME=∠BAE=60°,
∴∠BMD=60°.
又∵∠ABD=60°,∠BDM=∠ADB,
∴△ABD∽△BMD,
∴BD2=AD×DM.
24.如图,在矩形ABCD中,AB=3,∠CAB=30°,点P从点A出发,以每秒个单位长度的速度沿AB方向运动,点Q从点C出发,以每秒2个单位长度的速度沿对角线CA方向运动,已知P,Q两点同时出发,当点Q到达点A时,P,Q两点同时停止运动,连接PQ,设运动时间为t秒.
(1)BC= 3 ,AC= 6 .
(2)当t为何值时,△APQ的面积为;
(3)在运动过程中,是否存在一个时刻t,使所得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
(4)当点P关于点Q的对称点P′落在△ACD的内部(不包括边上)时,请求出t的取值范围.(直接写出答案)
【分析】(1)根据矩形的性质和含30°角的直角三角形的性质解答即可;
(2)根据直角三角形的性质和三角形的面积公式解答即可;
(3)分三种情况,利用翻折的性质解答即可;
(4)根据对称的性质解答即可.
【解答】(1)解:∵矩形ABCD,AB=3,∠CAB=30°,
∴BC=3,AC=6;
故答案为:3;6;
(2)解:过点Q作QH⊥AB,垂足为H,
由题意知,AP=t,AQ=6﹣2t,
在Rt△AQH中,∠QAP=30°,
∴QH=AQ=3﹣t,
∴,
解得:t1=1,t2=2;
(3)解:①当沿PQ翻折时,则AP=AQ,则,
解得:t=,
②当沿AP翻折时,则AQ=QP,过点Q作QM⊥AB,垂足为M,
则AM=AP=t,
在Rt△AQM中,∠QAM=30°,
∴,
解得:t=2,
③当沿AQ翻折时,则AP=PQ,
过点P作PM⊥AC,垂足为M,
则AM=AQ=3﹣t,
在Rt△AMP中,∠PAM=30°,
∴3﹣t=,
解得:t=,
综上所述,t的值为12﹣6或2或;
(4)由题意知,AP=t,AQ=6﹣2t,
∴P'在△ACD中,满足,
∴1.5<t<2.
同课章节目录
