6.3向心加速度同步练习题(word版含答案)
文档属性
| 名称 | 6.3向心加速度同步练习题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 936.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-22 00:00:00 | ||
图片预览




文档简介
6.3 向心加速度
一、单选题
1.如图所示,质量相等的甲、乙两人分别站在赤道和纬度为的地面上,他们随地球一起绕地轴做匀速圆周运动,则下列物理量相同的是( )
A.线速度 B.角速度 C.向心力 D.向心加速度
2.一质量为1kg的物体在水平面内做匀速圆周运动,圆周运动的半径为0.5m,物体旋转6周用时1min,则下列说法正确的是( )
A.物体做圆周运动的角速度大小为
B.物体做圆周运动的线速度大小为
C.物体做圆周运动的向心力大小为
D.物体做圆周运动的向心加速度大小为
3.如图所示,电动玩具小车在水平桌面上做匀速圆周运动。下列物理量中,可以用来描述小车运动变化快慢的是( )
A.位移 B.路程 C.角速度 D.向心加速度
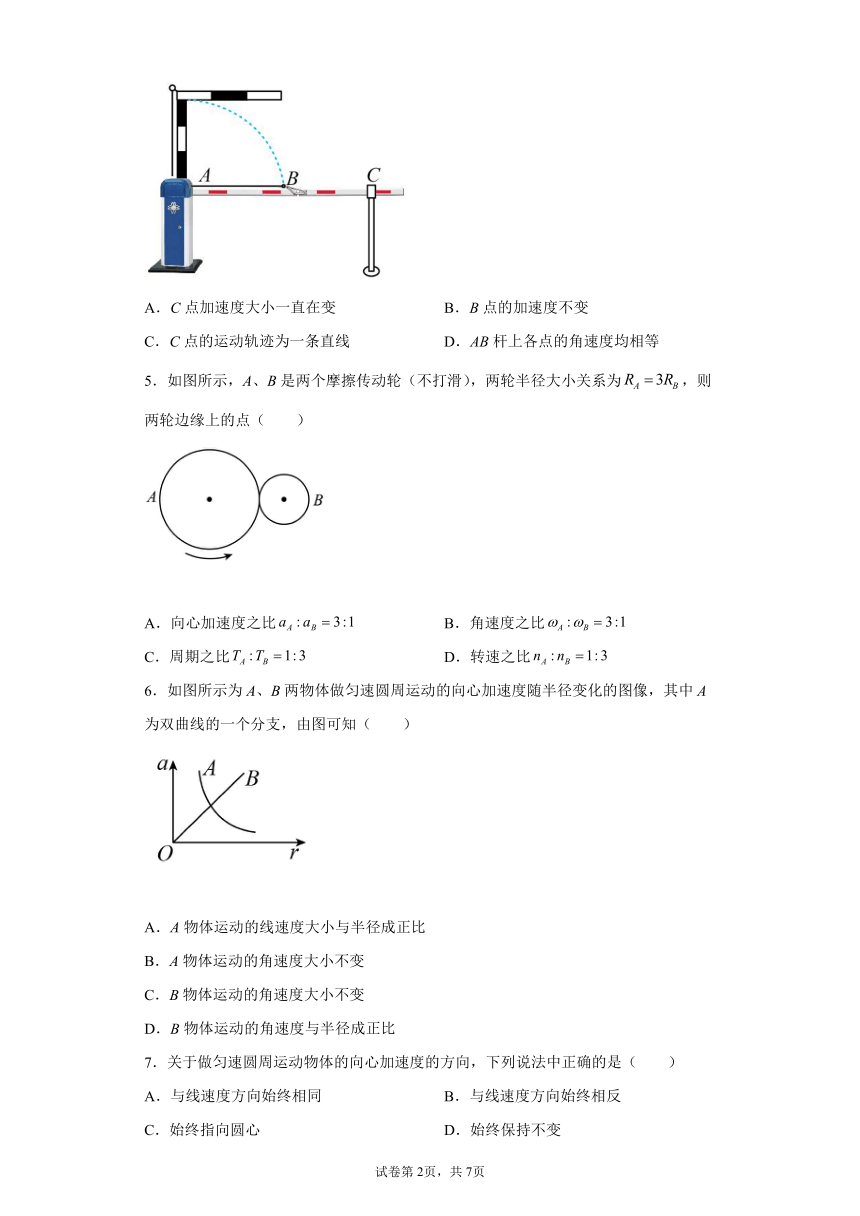
4.地下车库为了限制车辆高度,现已采用如图所示曲杆道闸。道闸总长3m,由相同长度的转动杆AB与横杆BC组成。B、C为横杆的两个端点,道闸工作期间,横杆BC始终保持水平,转动杆AB绕A点匀速转动过程中,下列说法正确的是( )
A.C点加速度大小一直在变 B.B点的加速度不变
C.C点的运动轨迹为一条直线 D.AB杆上各点的角速度均相等
5.如图所示,A、B是两个摩擦传动轮(不打滑),两轮半径大小关系为,则两轮边缘上的点( )
A.向心加速度之比 B.角速度之比
C.周期之比 D.转速之比
6.如图所示为A、B两物体做匀速圆周运动的向心加速度随半径变化的图像,其中A为双曲线的一个分支,由图可知( )
A.A物体运动的线速度大小与半径成正比
B.A物体运动的角速度大小不变
C.B物体运动的角速度大小不变
D.B物体运动的角速度与半径成正比
7.关于做匀速圆周运动物体的向心加速度的方向,下列说法中正确的是( )
A.与线速度方向始终相同 B.与线速度方向始终相反
C.始终指向圆心 D.始终保持不变
8.图为“天津之眼”摩天轮,游客某时刻位于匀速转动的摩天轮的最顶端,则从此时刻起游客的向心加速度( )
A.大小不变 B.逐渐减小
C.逐渐增大 D.先减小再增大
9.如图所示,一个圆盘在水平面内匀速转动,盘面上有两个小物块A、B,它们距圆盘中心的距离分别为r和2r,它们随圆盘一起匀速转动,关于小物块A、B各物理量之比正确的是( )
A.角速度之比ωA∶ ωB=1∶1
B.周期之比TA∶ TB=1∶2
C.线速度之比vA∶ vB=1∶1
D.向心加速度之比aA∶ aB=2∶1
二、多选题
10.和谐号动车经过一段弯道时,显示屏上显示的速率是216km/h。某乘客利用智能手机自带的指南针正在进行定位,他发现“指南针”的指针在5s内匀速转过了9°。则在此5s时间内,动车( )
A.转过的角度 B.转弯半径为
C.角速度为 D.向心加速度约为
11.如图所示,A、B两物块放在圆盘上,两物块到圆盘中心的距离:现让圆盘在水平面内做匀速圆周运动,两物块相对圆盘静止。下列说法中正确的是( )
A.两物块的线速度大小相等 B.两物块的角速度相等
C.两物块的周期相等 D.两物块的向心加速度大小相等
12.关于做匀速圆周运动物体的向心加速度方向,下列说法正确的是( )
A.与线速度方向始终垂直 B.与线速度方向始终相同
C.始终指向圆心 D.始终保持不变
13.如图所示是磁带录音机的磁带盒的示意图,A、B为缠绕磁带的两个轮子边缘上的点,两轮的半径均为r,在放音结束时,磁带全部绕到了B点所在的轮上,磁带的外缘半径R=3r,C为磁带外缘上的一点。现在进行倒带,则此时( )
A.A、B、C 三点的周期之比为 3:1:3
B.A、B、C 三点的线速度之比为 3:1:3
C.A、B、C 三点的角速度之比为 1:3:3
D.A、B、C 三点的向心加速度之比为 9:1:3
14.如图所示为学员驾驶汽车在水平面上绕点做匀速圆周运动的俯视示意图。已知质量为60kg的学员在A点位置,质量为70kg的教练员在B点位置,A点的转弯半径为5.0m,B点的转弯半径为4.0,学员和教练员(均可视为质点)( )
A.运动周期之比为4:5
B.运动线速度大小之比为5:4
C.向心加速度大小之比为4:5
D.受到的合力大小之比为15:14
三、填空题
15.在绕竖直轴匀速转动的圆环上有A、B两点,如右图所示,过A、B的半径与竖直轴的夹角分别为30°和60°,则A、B两点的线速度之比为___________;向心加速度之比为___________。
16.如图所示,一质点在的时间沿半径为的圆形轨道从点运动到点,质点与圆心的连线在这段时间内转过的角度为,该过程中质点可以看成匀速圆周运动,质点的角速度为______,向心加速度为______。
17.向心力只改变速度的_____,向心加速度只表示改变速度_____的快慢.
四、解答题
18.如图所示,一轻杆一端固定在转轴O上,在距O点为杆长的处固定一小球,轻杆以角速度ω绕O点在竖直平面内匀速转动。在杆转过的圆心角为θ的时间内,杆的端点通过的弧长为s,求:
(1)小球的线速度大小;
(2)小球的向心加速度大小。
19.如图所示,一轿车以30m/s的速率沿半径为60m的圆跑道行驶,当轿车从A运动到B时,轿车和圆心的连线转过的角度为90°,求:
(1)此过程中轿车的位移大小;
(2)此过程中轿车通过的路程;
(3)轿车运动的向心加速度大小.
20.一个圆盘在水平面内匀速转动,角速度是4 rad/s,盘面上距盘中心0.01 m的位置有一个质量为0.1 kg的小物体能够随盘一起转动,如图所示。求物体转动的向心加速度的大小和方向。
21.根据,v的方向即为Δt时间内平均加速度的方向,当Δt趋近于0时,v的方向即为某时刻瞬时加速度的方向。我们可以通过观察不断缩小的时间段内的平均加速度方向的方法,来逼近某点的瞬时加速度方向。图中圆弧是某一质点绕O点沿顺时针方向做匀速圆周运动的轨迹,若质点在t时间内从A点经过一段劣弧运动到B点。
(1)请用铅笔画出质点从A点起在时间t内速度变化量v的方向;
(2)质点从A到B的时间t内平均加速度a1的方向与AB连线是平行还是垂直?
(3)请用铅笔画出质点经过A点时瞬时加速度aA的方向,并说明理由。
试卷第6页,共7页
试卷第7页,共7页
参考答案
1.B
【详解】
AB.甲乙两人站在地球上都随地球转动,角速度均与地球自转角速度相等,由可知,甲做圆周运动的半径较大,线速度较大,A错误,B正确;
CD.做匀速圆周运动的向心力、向心加速度可表示为
,
由于甲、乙做圆周运动的半径不相等,则向心力、向心加速度大小均不相等,CD错误。
故选B。
2.B
【详解】
A.物体做圆周运动的周期为
故A错误。
B.线速度大小
故B正确。
C.向心力大小
故C错误。
D.向心加速度
故D错误。
故选B。
3.D
【详解】
A.位移是描述物体位置的变化,故A不符合题意;
B.路程是运动轨迹的长度,故B不符合题意;
C.角速度是描述小车运动快慢的物理量,故C不符合题意;
D.向心加速度可以用来描述小车运动变化快慢,故D符合题意。
故选D。
4.D
【详解】
A.转动杆AB绕A点匀速转动过程中,横杆BC始终保持水平,BC两个端点相对静止,因此C端点做匀速圆周运动,加速度大小不变,A错误;
B.B点做匀速圆周运动,加速度大小不变,方向指向圆心,时刻改变,B错误;
C.根据前面选项分析,C点做匀速圆周运动,C错误;
D.根据前面选项分析,转动杆AB上各点属于共轴传动,角速度相等,D正确。
故选D。
5.D
【详解】
两轮是同缘转动,则线速度相等,根据
可知,向心加速度之比
根据
v=ωr
可知,角速度之比
根据
可知,周期之比
根据
转速之比
故选D。
6.C
【详解】
AB.因为A为双曲线的一个分支,可知A物体的向心加速度与半径成反比,根据
可知 A物体运动的线速度大小不变,选项AB错误;
CD.因为B是过原点的直线,可知B物体运动的向心加速度与半径成正比,根据
可知,B物体运动的角速度大小不变,选项C正确,D错误。
故选C。
7.C
【详解】
AB.向心加速度的方向与线速度方向垂直,选项AB错误;
CD.做匀速圆周运动物体的向心加速度的大小不变,而方向时刻变化,始终指向圆心,选项C正确,D错误。
故选C。
8.A
【详解】
做圆周运动的向心加速度表达式为
而游客做匀速圆周运动,则线速度大小不变,故向心加速度大小不变,故选A。
9.A
【详解】
两物体同轴转动,则角速度相等,即角速度之比
ωA∶ ωB=1∶1
根据
可知周期之比
TA∶ TB=1∶1
根据
v=ωr
可知,线速度之比
vA∶ vB=1∶2
根据
a=ωv
可知向心加速度之比
aA∶ aB=1∶2
故选A。
10.BC
【详解】
A.转过的角度,根据
A错误;
C.角速度为
C正确;
B.根据
解得
B正确;
D.根据
D错误。
故选BC。
11.BC
【详解】
两物块同轴转动,则角速度相等,根据
可知,周期相等,根据
v=ωr
可知,线速度不相等;根据
可知,两物块的向心加速度大小不相等。
故选BC。
12.AC
【详解】
向心加速度的方向始终指向圆心,和线速度的方向垂直,不改变线速度的大小只是改变线速度的方向,由于加速度是矢量,因此向心加速度是时刻变化的,选项BD错误,AC正确。
故选AC。
13.BD
【详解】
A.靠传送带传动轮子边缘上的点具有相同的线速度,故A、C两点的线速度相等,即
vA:vC=1:1
C的半径是A的半径的3倍,根据
v=rω
知
ωA:ωC=3:1
B与C属于同轴转动,所以
ωB=ωC
根据周期与角速度的关系
所以
ωB=ωC
则
TB=TC
所以A、B、C三点的周期之比1:3:3,故A错误;
B.B与C的角速度相等,由
v=ωr
可知
vB:vC=1:3
所以A、B、C三点的线速度之比3:1:3.故B正确;
C.由于
ωA:ωC=3:1
ωB=ωC
所以A、B、C三点的角速度之比3:1:1.故C错误;
D.向心加速度
a=ω v
所以
aA:aB:aC=ωAvA:ωBvB:ωCvC=3×3:1×1:1×3=9:1:3
故D正确。
故选BD。
14.BD
【详解】
A.A、B两点做圆周运动的角速度相等,根据T=知,周期相等,故A项错误;
B.根据知,半径之比为5:4,则线速度之比为5:4,故B项正确;
C.根据2知,半径之比为5:4,则向心加速度大小之比为5:4,故C项错误;
D.根据知,向心加速度大小之比为5:4,质量之比为6:7,则合力大小之比为15:14,故D项正确。
故选BD。
15.
【详解】
A、B两点做圆周运动的半径分别为
它们的角速度相同,所以线速度之比为
加速度之比为
16.
【详解】
根据
解得
根据
解得
17.方向 方向
【详解】
向心力的方向始终与物体运动的方向垂直,所以只改变运动的方向,不改变物体速度的大小;
向心加速度只改变物体的速度的方向不改变速度的大小,其物理意义是描述线速度方向变化的快慢.
18.(1);(2)
【详解】
(1)杆的端点以杆长为半径做圆周运动,求解杆长为
小球的转动半径为,小球做圆周运动的角速度与杆转动的角速度相同,则小球转动的线速度为
(2)小球的向心加速度
19.(1) (2) m (3)
【详解】
试题分析:(1) 位移是从初位置到末位置的有向线段;
(2) 路程是轨迹的实际长度,等于圆弧长度;
(3) 根据求解向心加速度的大小.
如图所示,v=30m/s,r=60m,θ=90°
(1) 轿车的位移为从初位置A到末位置B的有向线段的长度;
(2) 路程等于弧长 ;
(3) 向心加速度大小
20.0.16m/s2,方向指向圆心
【详解】
向心加速度的大小为
方向沿半径指向圆心
21.(1);(2)垂直;(3),理由见解析
【详解】
(1)质点从A点起在时间t内速度变化量v的方向,如图中红线所示
(2)质点从A到B的时间t内平均加速度a为
即平均加速度的方向与速度变化量的方向相同。方向与半径OA垂直,方向与半径OB垂直,与速度的矢量三角形相似,所以与AB垂直。
(3)质点经过A点时瞬时加速度aA的方向如图
根据加速度的定义式知,质点做匀速圆周运动的平均加速度为
当趋近于0时,加速度a就表示质点A的瞬时加速度。由(2)分析可知,与两质点的连线相互垂直,当趋近于0时,两质点间的距离逐渐减小为0,则此时的瞬时加速度方向将指向圆心。答案第10页,共1页
答案第9页,共9页
一、单选题
1.如图所示,质量相等的甲、乙两人分别站在赤道和纬度为的地面上,他们随地球一起绕地轴做匀速圆周运动,则下列物理量相同的是( )
A.线速度 B.角速度 C.向心力 D.向心加速度
2.一质量为1kg的物体在水平面内做匀速圆周运动,圆周运动的半径为0.5m,物体旋转6周用时1min,则下列说法正确的是( )
A.物体做圆周运动的角速度大小为
B.物体做圆周运动的线速度大小为
C.物体做圆周运动的向心力大小为
D.物体做圆周运动的向心加速度大小为
3.如图所示,电动玩具小车在水平桌面上做匀速圆周运动。下列物理量中,可以用来描述小车运动变化快慢的是( )
A.位移 B.路程 C.角速度 D.向心加速度
4.地下车库为了限制车辆高度,现已采用如图所示曲杆道闸。道闸总长3m,由相同长度的转动杆AB与横杆BC组成。B、C为横杆的两个端点,道闸工作期间,横杆BC始终保持水平,转动杆AB绕A点匀速转动过程中,下列说法正确的是( )
A.C点加速度大小一直在变 B.B点的加速度不变
C.C点的运动轨迹为一条直线 D.AB杆上各点的角速度均相等
5.如图所示,A、B是两个摩擦传动轮(不打滑),两轮半径大小关系为,则两轮边缘上的点( )
A.向心加速度之比 B.角速度之比
C.周期之比 D.转速之比
6.如图所示为A、B两物体做匀速圆周运动的向心加速度随半径变化的图像,其中A为双曲线的一个分支,由图可知( )
A.A物体运动的线速度大小与半径成正比
B.A物体运动的角速度大小不变
C.B物体运动的角速度大小不变
D.B物体运动的角速度与半径成正比
7.关于做匀速圆周运动物体的向心加速度的方向,下列说法中正确的是( )
A.与线速度方向始终相同 B.与线速度方向始终相反
C.始终指向圆心 D.始终保持不变
8.图为“天津之眼”摩天轮,游客某时刻位于匀速转动的摩天轮的最顶端,则从此时刻起游客的向心加速度( )
A.大小不变 B.逐渐减小
C.逐渐增大 D.先减小再增大
9.如图所示,一个圆盘在水平面内匀速转动,盘面上有两个小物块A、B,它们距圆盘中心的距离分别为r和2r,它们随圆盘一起匀速转动,关于小物块A、B各物理量之比正确的是( )
A.角速度之比ωA∶ ωB=1∶1
B.周期之比TA∶ TB=1∶2
C.线速度之比vA∶ vB=1∶1
D.向心加速度之比aA∶ aB=2∶1
二、多选题
10.和谐号动车经过一段弯道时,显示屏上显示的速率是216km/h。某乘客利用智能手机自带的指南针正在进行定位,他发现“指南针”的指针在5s内匀速转过了9°。则在此5s时间内,动车( )
A.转过的角度 B.转弯半径为
C.角速度为 D.向心加速度约为
11.如图所示,A、B两物块放在圆盘上,两物块到圆盘中心的距离:现让圆盘在水平面内做匀速圆周运动,两物块相对圆盘静止。下列说法中正确的是( )
A.两物块的线速度大小相等 B.两物块的角速度相等
C.两物块的周期相等 D.两物块的向心加速度大小相等
12.关于做匀速圆周运动物体的向心加速度方向,下列说法正确的是( )
A.与线速度方向始终垂直 B.与线速度方向始终相同
C.始终指向圆心 D.始终保持不变
13.如图所示是磁带录音机的磁带盒的示意图,A、B为缠绕磁带的两个轮子边缘上的点,两轮的半径均为r,在放音结束时,磁带全部绕到了B点所在的轮上,磁带的外缘半径R=3r,C为磁带外缘上的一点。现在进行倒带,则此时( )
A.A、B、C 三点的周期之比为 3:1:3
B.A、B、C 三点的线速度之比为 3:1:3
C.A、B、C 三点的角速度之比为 1:3:3
D.A、B、C 三点的向心加速度之比为 9:1:3
14.如图所示为学员驾驶汽车在水平面上绕点做匀速圆周运动的俯视示意图。已知质量为60kg的学员在A点位置,质量为70kg的教练员在B点位置,A点的转弯半径为5.0m,B点的转弯半径为4.0,学员和教练员(均可视为质点)( )
A.运动周期之比为4:5
B.运动线速度大小之比为5:4
C.向心加速度大小之比为4:5
D.受到的合力大小之比为15:14
三、填空题
15.在绕竖直轴匀速转动的圆环上有A、B两点,如右图所示,过A、B的半径与竖直轴的夹角分别为30°和60°,则A、B两点的线速度之比为___________;向心加速度之比为___________。
16.如图所示,一质点在的时间沿半径为的圆形轨道从点运动到点,质点与圆心的连线在这段时间内转过的角度为,该过程中质点可以看成匀速圆周运动,质点的角速度为______,向心加速度为______。
17.向心力只改变速度的_____,向心加速度只表示改变速度_____的快慢.
四、解答题
18.如图所示,一轻杆一端固定在转轴O上,在距O点为杆长的处固定一小球,轻杆以角速度ω绕O点在竖直平面内匀速转动。在杆转过的圆心角为θ的时间内,杆的端点通过的弧长为s,求:
(1)小球的线速度大小;
(2)小球的向心加速度大小。
19.如图所示,一轿车以30m/s的速率沿半径为60m的圆跑道行驶,当轿车从A运动到B时,轿车和圆心的连线转过的角度为90°,求:
(1)此过程中轿车的位移大小;
(2)此过程中轿车通过的路程;
(3)轿车运动的向心加速度大小.
20.一个圆盘在水平面内匀速转动,角速度是4 rad/s,盘面上距盘中心0.01 m的位置有一个质量为0.1 kg的小物体能够随盘一起转动,如图所示。求物体转动的向心加速度的大小和方向。
21.根据,v的方向即为Δt时间内平均加速度的方向,当Δt趋近于0时,v的方向即为某时刻瞬时加速度的方向。我们可以通过观察不断缩小的时间段内的平均加速度方向的方法,来逼近某点的瞬时加速度方向。图中圆弧是某一质点绕O点沿顺时针方向做匀速圆周运动的轨迹,若质点在t时间内从A点经过一段劣弧运动到B点。
(1)请用铅笔画出质点从A点起在时间t内速度变化量v的方向;
(2)质点从A到B的时间t内平均加速度a1的方向与AB连线是平行还是垂直?
(3)请用铅笔画出质点经过A点时瞬时加速度aA的方向,并说明理由。
试卷第6页,共7页
试卷第7页,共7页
参考答案
1.B
【详解】
AB.甲乙两人站在地球上都随地球转动,角速度均与地球自转角速度相等,由可知,甲做圆周运动的半径较大,线速度较大,A错误,B正确;
CD.做匀速圆周运动的向心力、向心加速度可表示为
,
由于甲、乙做圆周运动的半径不相等,则向心力、向心加速度大小均不相等,CD错误。
故选B。
2.B
【详解】
A.物体做圆周运动的周期为
故A错误。
B.线速度大小
故B正确。
C.向心力大小
故C错误。
D.向心加速度
故D错误。
故选B。
3.D
【详解】
A.位移是描述物体位置的变化,故A不符合题意;
B.路程是运动轨迹的长度,故B不符合题意;
C.角速度是描述小车运动快慢的物理量,故C不符合题意;
D.向心加速度可以用来描述小车运动变化快慢,故D符合题意。
故选D。
4.D
【详解】
A.转动杆AB绕A点匀速转动过程中,横杆BC始终保持水平,BC两个端点相对静止,因此C端点做匀速圆周运动,加速度大小不变,A错误;
B.B点做匀速圆周运动,加速度大小不变,方向指向圆心,时刻改变,B错误;
C.根据前面选项分析,C点做匀速圆周运动,C错误;
D.根据前面选项分析,转动杆AB上各点属于共轴传动,角速度相等,D正确。
故选D。
5.D
【详解】
两轮是同缘转动,则线速度相等,根据
可知,向心加速度之比
根据
v=ωr
可知,角速度之比
根据
可知,周期之比
根据
转速之比
故选D。
6.C
【详解】
AB.因为A为双曲线的一个分支,可知A物体的向心加速度与半径成反比,根据
可知 A物体运动的线速度大小不变,选项AB错误;
CD.因为B是过原点的直线,可知B物体运动的向心加速度与半径成正比,根据
可知,B物体运动的角速度大小不变,选项C正确,D错误。
故选C。
7.C
【详解】
AB.向心加速度的方向与线速度方向垂直,选项AB错误;
CD.做匀速圆周运动物体的向心加速度的大小不变,而方向时刻变化,始终指向圆心,选项C正确,D错误。
故选C。
8.A
【详解】
做圆周运动的向心加速度表达式为
而游客做匀速圆周运动,则线速度大小不变,故向心加速度大小不变,故选A。
9.A
【详解】
两物体同轴转动,则角速度相等,即角速度之比
ωA∶ ωB=1∶1
根据
可知周期之比
TA∶ TB=1∶1
根据
v=ωr
可知,线速度之比
vA∶ vB=1∶2
根据
a=ωv
可知向心加速度之比
aA∶ aB=1∶2
故选A。
10.BC
【详解】
A.转过的角度,根据
A错误;
C.角速度为
C正确;
B.根据
解得
B正确;
D.根据
D错误。
故选BC。
11.BC
【详解】
两物块同轴转动,则角速度相等,根据
可知,周期相等,根据
v=ωr
可知,线速度不相等;根据
可知,两物块的向心加速度大小不相等。
故选BC。
12.AC
【详解】
向心加速度的方向始终指向圆心,和线速度的方向垂直,不改变线速度的大小只是改变线速度的方向,由于加速度是矢量,因此向心加速度是时刻变化的,选项BD错误,AC正确。
故选AC。
13.BD
【详解】
A.靠传送带传动轮子边缘上的点具有相同的线速度,故A、C两点的线速度相等,即
vA:vC=1:1
C的半径是A的半径的3倍,根据
v=rω
知
ωA:ωC=3:1
B与C属于同轴转动,所以
ωB=ωC
根据周期与角速度的关系
所以
ωB=ωC
则
TB=TC
所以A、B、C三点的周期之比1:3:3,故A错误;
B.B与C的角速度相等,由
v=ωr
可知
vB:vC=1:3
所以A、B、C三点的线速度之比3:1:3.故B正确;
C.由于
ωA:ωC=3:1
ωB=ωC
所以A、B、C三点的角速度之比3:1:1.故C错误;
D.向心加速度
a=ω v
所以
aA:aB:aC=ωAvA:ωBvB:ωCvC=3×3:1×1:1×3=9:1:3
故D正确。
故选BD。
14.BD
【详解】
A.A、B两点做圆周运动的角速度相等,根据T=知,周期相等,故A项错误;
B.根据知,半径之比为5:4,则线速度之比为5:4,故B项正确;
C.根据2知,半径之比为5:4,则向心加速度大小之比为5:4,故C项错误;
D.根据知,向心加速度大小之比为5:4,质量之比为6:7,则合力大小之比为15:14,故D项正确。
故选BD。
15.
【详解】
A、B两点做圆周运动的半径分别为
它们的角速度相同,所以线速度之比为
加速度之比为
16.
【详解】
根据
解得
根据
解得
17.方向 方向
【详解】
向心力的方向始终与物体运动的方向垂直,所以只改变运动的方向,不改变物体速度的大小;
向心加速度只改变物体的速度的方向不改变速度的大小,其物理意义是描述线速度方向变化的快慢.
18.(1);(2)
【详解】
(1)杆的端点以杆长为半径做圆周运动,求解杆长为
小球的转动半径为,小球做圆周运动的角速度与杆转动的角速度相同,则小球转动的线速度为
(2)小球的向心加速度
19.(1) (2) m (3)
【详解】
试题分析:(1) 位移是从初位置到末位置的有向线段;
(2) 路程是轨迹的实际长度,等于圆弧长度;
(3) 根据求解向心加速度的大小.
如图所示,v=30m/s,r=60m,θ=90°
(1) 轿车的位移为从初位置A到末位置B的有向线段的长度;
(2) 路程等于弧长 ;
(3) 向心加速度大小
20.0.16m/s2,方向指向圆心
【详解】
向心加速度的大小为
方向沿半径指向圆心
21.(1);(2)垂直;(3),理由见解析
【详解】
(1)质点从A点起在时间t内速度变化量v的方向,如图中红线所示
(2)质点从A到B的时间t内平均加速度a为
即平均加速度的方向与速度变化量的方向相同。方向与半径OA垂直,方向与半径OB垂直,与速度的矢量三角形相似,所以与AB垂直。
(3)质点经过A点时瞬时加速度aA的方向如图
根据加速度的定义式知,质点做匀速圆周运动的平均加速度为
当趋近于0时,加速度a就表示质点A的瞬时加速度。由(2)分析可知,与两质点的连线相互垂直,当趋近于0时,两质点间的距离逐渐减小为0,则此时的瞬时加速度方向将指向圆心。答案第10页,共1页
答案第9页,共9页
