2021-2022学年人教版九年级数学下册第二十七章相似 单元测试训练卷(word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十七章相似 单元测试训练卷(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 00:00:00 | ||
图片预览



文档简介
人教版九年级数学下册
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 观察下列每组图形,相似图形是( )
2. 在平面直角坐标系中,作点A(3,4)关于x轴对称的点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3)
C.(-3,4) D.(-3,-4)
3. 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F,若=,DE=6,则EF的长是( )
A.8 B.9
C.10 D.12
4. 如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C.= D.=
5. 在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB缩小到原来的,则点P的对应点的坐标为( )
A.(2m,2n) B.(2m,2n)或(-2m,-2n)
C.(m,n) D.(m,n)或(-m,-n)
6. 如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为点P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP
C.线段AB D.线段AD
7. 如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则C1D1的长是( )
A.10 B.12
C. D.
8. 将一个三角形和一个矩形按照如图所示的方式扩大,使它们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )
A.新三角形与原三角形相似
B.新矩形与原矩形相似
C.新三角形与原三角形、新矩形与原矩形都相似
D.新三角形与原三角形、新矩形与原矩形都不相似
9.如图,在△ABC中,中线BE,CD相交于点O,连结DE,下列结论:①=;②=;③=;④=.其中正确的个数有( )
A.1个 B.2个
C.3个 D.4个
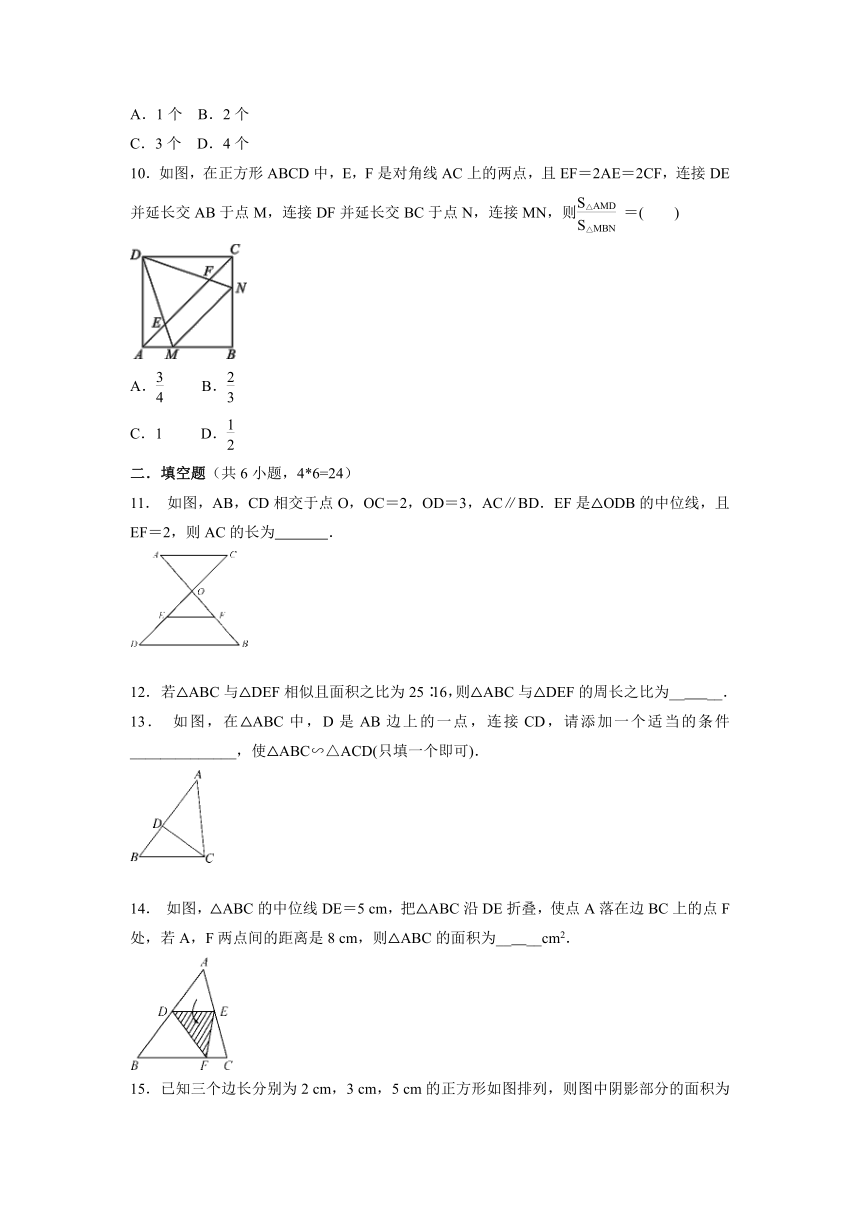
10.如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则=( )
A. B.
C.1 D.
二.填空题(共6小题,4*6=24)
11. 如图,AB,CD相交于点O,OC=2,OD=3,AC∥BD.EF是△ODB的中位线,且EF=2,则AC的长为 .
12. 若△ABC与△DEF相似且面积之比为25∶16,则△ABC与△DEF的周长之比为__ __.
13. 如图,在△ABC中,D是AB边上的一点,连接CD,请添加一个适当的条件______________,使△ABC∽△ACD(只填一个即可).
14. 如图,△ABC的中位线DE=5 cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A,F两点间的距离是8 cm,则△ABC的面积为__ __cm2.
15.已知三个边长分别为2 cm,3 cm,5 cm的正方形如图排列,则图中阴影部分的面积为_________ cm2.
16.如图,将边长为6 cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是________cm.
三.解答题(共5小题, 56分)
17.(6分) 如图,DE∥BC,EC=AD,AE=2 cm,AB=7.5 cm,求DB的长.
18.(8分) 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.
19.(8分) 如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=FC,连结EF交BC的延长线于点G.
(1)试说明:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
20.(10分) 如图,身高1.5 m的琪琪站在离河边3 m的B处时,恰好能看到对岸边电线杆GM的全部倒影KM,若河岸高出水面高度ED为 0.75 m,电线杆高MG为4.5 m,求河宽EM.
21.(12分) 正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn按如图所示的位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
(1)写出正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心坐标;
(2)求正方形A4A5B4C4四个顶点的坐标.
22.(12分) 如图①,四边形ABCD的对角线AC,BD交于点O,OB=OD,OC=OA+AB,AD=m,BC=n,∠ABD+∠ADB=∠ACB.
(1)填空:∠BAD与∠ACB的数量关系为____________________;
(2)求的值;
(3)将△ACD沿CD翻折,得到△A′CD(如图②),连接BA′,与CD交于点P,若CD=,求PC的长.
参考答案
1-5DDBDD 6-10CCABA
11.
12.5∶4
13.∠B=∠ACD或∠ADC=∠ACB或AC2=AD·AB
14.40
15.3.75
16.12
17.解:∵DE∥BC,∴=.∵EC=AD,AE=2 cm,AB=7.5 cm,∴=,解得BD=4.5 cm(BD=12.5 cm舍去).
18.解:(1)△A1BC1如图所示.
(2)△A2B2C2如图所示,点C2的坐标为(-6,4).
19.解:(1)易证=,=,又∠D=∠A=90°,∴△ABE∽△DEF
(2)DE∥CG,∴△DEF∽△CGF,∴==,又∵DE=AD=2,∴CG=6,∴BG=BC+CG=4+6=10
20. 解:∵AB∥DE∥MK,∴△ACF∽△DEF∽△KMF,∴===,===,设EF=x m,则MF=6x m,由2CF=MF,得2(x+3)=6x,解得x=,∴MF=9 m,∴EM=+9=10.5(m),即河宽EM为10.5 m.
21. 解:(1)如图所示,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心坐标为(0,0).
(2)∵点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0),∴OA1=A1C1=1,OA2=A2C2=2,OA3=A3C3=4,∴可得OA4=A4C4=8,OA5=16,故正方形A4A5B4C4四个顶点的坐标分别为A4(8,0),A5(16,0),B4(16,8),C4(8,8).
22.解:(1)∠BAD+∠ACB=180°
(2)过点D作DE∥AB,交AC于点E,则∠OAB=∠OED,∠OBA=∠ODE.又∵OB=OD,
∴△OAB≌△OED.∴AB=ED,OA=OE.∵OC=OA+AB=OE+CE,∴AB=CE.设AB=ED=CE=x,OA=OE=y.∵DE∥AB,∴∠EDA+∠DAB=180°.由(1)知∠BAD+∠ACB=180°,∴∠EDA=∠ACB.∵∠DEA=∠CAB,∴△EAD∽△ABC.∴===,即=,整理,得4y2+2xy-x2=0,∴+-1=0,解得=或=(不合题意,舍去).∴=.
(3)过点D作DE∥AB,交AC于点E.由(2)知,DE=CE,∴∠EDC=∠DCE.由翻折的性质,知∠DCA=∠DCA′,∠DAC=∠DA′C,A′D=AD.∴∠EDC=∠A′CD.∴DE∥CA′.∵AB∥DE,∴AB∥CA′.∴∠ABC+∠A′CB=180°.由(2)知△EAD∽△ABC,∴∠DAE=∠ABC=∠DA′C,∴∠DA′C+∠BCA′=180°,∴A′D∥BC,∴△PA′D∽△PBC.∴====.∴=,即=.∵CD=,∴PC=1.
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 观察下列每组图形,相似图形是( )
2. 在平面直角坐标系中,作点A(3,4)关于x轴对称的点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3)
C.(-3,4) D.(-3,-4)
3. 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F,若=,DE=6,则EF的长是( )
A.8 B.9
C.10 D.12
4. 如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C.= D.=
5. 在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB缩小到原来的,则点P的对应点的坐标为( )
A.(2m,2n) B.(2m,2n)或(-2m,-2n)
C.(m,n) D.(m,n)或(-m,-n)
6. 如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为点P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP
C.线段AB D.线段AD
7. 如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则C1D1的长是( )
A.10 B.12
C. D.
8. 将一个三角形和一个矩形按照如图所示的方式扩大,使它们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是( )
A.新三角形与原三角形相似
B.新矩形与原矩形相似
C.新三角形与原三角形、新矩形与原矩形都相似
D.新三角形与原三角形、新矩形与原矩形都不相似
9.如图,在△ABC中,中线BE,CD相交于点O,连结DE,下列结论:①=;②=;③=;④=.其中正确的个数有( )
A.1个 B.2个
C.3个 D.4个
10.如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则=( )
A. B.
C.1 D.
二.填空题(共6小题,4*6=24)
11. 如图,AB,CD相交于点O,OC=2,OD=3,AC∥BD.EF是△ODB的中位线,且EF=2,则AC的长为 .
12. 若△ABC与△DEF相似且面积之比为25∶16,则△ABC与△DEF的周长之比为__ __.
13. 如图,在△ABC中,D是AB边上的一点,连接CD,请添加一个适当的条件______________,使△ABC∽△ACD(只填一个即可).
14. 如图,△ABC的中位线DE=5 cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A,F两点间的距离是8 cm,则△ABC的面积为__ __cm2.
15.已知三个边长分别为2 cm,3 cm,5 cm的正方形如图排列,则图中阴影部分的面积为_________ cm2.
16.如图,将边长为6 cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是________cm.
三.解答题(共5小题, 56分)
17.(6分) 如图,DE∥BC,EC=AD,AE=2 cm,AB=7.5 cm,求DB的长.
18.(8分) 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.
19.(8分) 如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=FC,连结EF交BC的延长线于点G.
(1)试说明:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
20.(10分) 如图,身高1.5 m的琪琪站在离河边3 m的B处时,恰好能看到对岸边电线杆GM的全部倒影KM,若河岸高出水面高度ED为 0.75 m,电线杆高MG为4.5 m,求河宽EM.
21.(12分) 正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn按如图所示的位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
(1)写出正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心坐标;
(2)求正方形A4A5B4C4四个顶点的坐标.
22.(12分) 如图①,四边形ABCD的对角线AC,BD交于点O,OB=OD,OC=OA+AB,AD=m,BC=n,∠ABD+∠ADB=∠ACB.
(1)填空:∠BAD与∠ACB的数量关系为____________________;
(2)求的值;
(3)将△ACD沿CD翻折,得到△A′CD(如图②),连接BA′,与CD交于点P,若CD=,求PC的长.
参考答案
1-5DDBDD 6-10CCABA
11.
12.5∶4
13.∠B=∠ACD或∠ADC=∠ACB或AC2=AD·AB
14.40
15.3.75
16.12
17.解:∵DE∥BC,∴=.∵EC=AD,AE=2 cm,AB=7.5 cm,∴=,解得BD=4.5 cm(BD=12.5 cm舍去).
18.解:(1)△A1BC1如图所示.
(2)△A2B2C2如图所示,点C2的坐标为(-6,4).
19.解:(1)易证=,=,又∠D=∠A=90°,∴△ABE∽△DEF
(2)DE∥CG,∴△DEF∽△CGF,∴==,又∵DE=AD=2,∴CG=6,∴BG=BC+CG=4+6=10
20. 解:∵AB∥DE∥MK,∴△ACF∽△DEF∽△KMF,∴===,===,设EF=x m,则MF=6x m,由2CF=MF,得2(x+3)=6x,解得x=,∴MF=9 m,∴EM=+9=10.5(m),即河宽EM为10.5 m.
21. 解:(1)如图所示,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心坐标为(0,0).
(2)∵点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0),∴OA1=A1C1=1,OA2=A2C2=2,OA3=A3C3=4,∴可得OA4=A4C4=8,OA5=16,故正方形A4A5B4C4四个顶点的坐标分别为A4(8,0),A5(16,0),B4(16,8),C4(8,8).
22.解:(1)∠BAD+∠ACB=180°
(2)过点D作DE∥AB,交AC于点E,则∠OAB=∠OED,∠OBA=∠ODE.又∵OB=OD,
∴△OAB≌△OED.∴AB=ED,OA=OE.∵OC=OA+AB=OE+CE,∴AB=CE.设AB=ED=CE=x,OA=OE=y.∵DE∥AB,∴∠EDA+∠DAB=180°.由(1)知∠BAD+∠ACB=180°,∴∠EDA=∠ACB.∵∠DEA=∠CAB,∴△EAD∽△ABC.∴===,即=,整理,得4y2+2xy-x2=0,∴+-1=0,解得=或=(不合题意,舍去).∴=.
(3)过点D作DE∥AB,交AC于点E.由(2)知,DE=CE,∴∠EDC=∠DCE.由翻折的性质,知∠DCA=∠DCA′,∠DAC=∠DA′C,A′D=AD.∴∠EDC=∠A′CD.∴DE∥CA′.∵AB∥DE,∴AB∥CA′.∴∠ABC+∠A′CB=180°.由(2)知△EAD∽△ABC,∴∠DAE=∠ABC=∠DA′C,∴∠DA′C+∠BCA′=180°,∴A′D∥BC,∴△PA′D∽△PBC.∴====.∴=,即=.∵CD=,∴PC=1.
