2021-2022学年沪科版九年级数学上册22.4 图形的位似变换 测量与误差 复习练习(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册22.4 图形的位似变换 测量与误差 复习练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 00:00:00 | ||
图片预览



文档简介
22.4 图形的位似变换
一、选择题
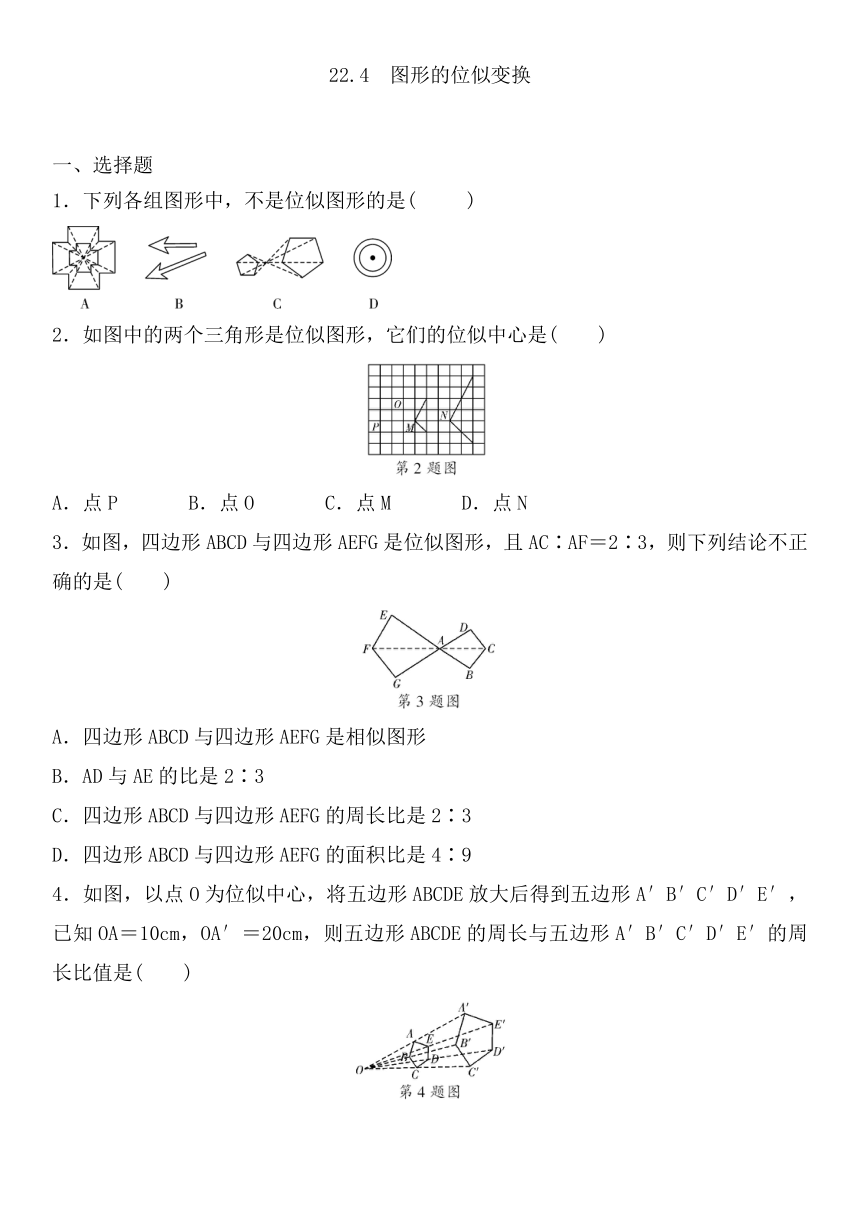
1.下列各组图形中,不是位似图形的是( )
2.如图中的两个三角形是位似图形,它们的位似中心是( )
A.点P B.点O C.点M D.点N
3.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是( )
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2∶3
C.四边形ABCD与四边形AEFG的周长比是2∶3
D.四边形ABCD与四边形AEFG的面积比是4∶9
4.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比值是( )
A. B. C. D.
5.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8)、B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1) B.(4,3) C.(3,4) D.(1,5)
6.如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-1,2) B.(-9,18) C.(-9,18)或(9,-18) D.(-1,2)或(1,-2)
7.如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,边OC在y轴上.如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于OABC的面积的,则点B的对应点B′的坐标为( )
A.(-2,3) B.(2,-3)
C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
8.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
9.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=8,则S△A′B′C′等于( )
A.15 B.16 C.17 D.18
二、填空题
10.在平面直角坐标系中,△ABC顶点A的坐标为(2,3),若以原点O为位似中心,画△AEC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比等于,则点A′的坐标为________.
11.如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是________.
12. 如图,点O是等边△PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形,此时△P′Q′R′与△PQR的位似比为 、位似中心为 .
13. 如图所示,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,点A、B、A′、B′均在图中格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为 .
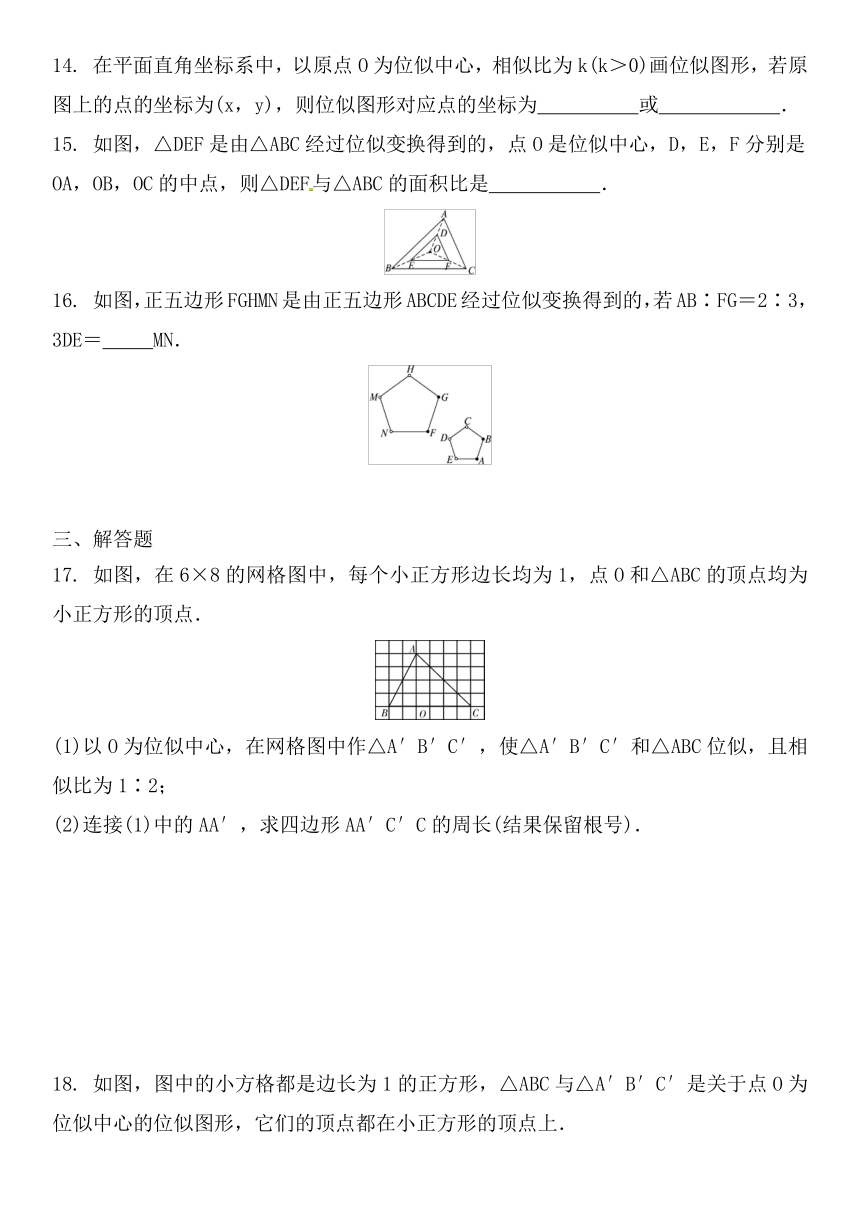
14. 在平面直角坐标系中,以原点O为位似中心,相似比为k(k>0)画位似图形,若原图上的点的坐标为(x,y),则位似图形对应点的坐标为 或 .
15. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是 .
16. 如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB∶FG=2∶3,3DE= MN.
三、解答题
17. 如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且相似比为1∶2;
(2)连接(1)中的AA′,求四边形AA′C′C的周长(结果保留根号).
18. 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心O;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1∶5.
19. 如图,在边长为1个单位长度的小正方形网格中.
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1;
(2)以B为位似中心,将△ABC放大为原来的2倍,得到△A2BC2,请在网格中画出△A2BC2;
(3)求△CC1C2的面积.
20. 如下图所示的平面直角坐标系中,
(1)描出下列各点:A(1,0)、B(3,0)、C(3,3)、D(0,1),并将这些点用线段依次连接起来;
(2)以坐标原点O为位似中心,把(1)中所得图形放大两倍.
答案:
一、
1-9 BABDC DDAD
二、
10. (4,6)或(-4,-6)
11. (-2,0)
12. 点O
13. (,)
14. (kx,ky) (-kx,-ky)
15. 1∶4
16. 2
三、
17. 解:(1)如图:
(2)四边形AA′C′C的周长=4+6.
18. 解:(1)略;
(2)1∶2;
(3)画图略,寻找A1、B1、C1的方法是===5即可.
19. 解:(1)(2)如图:
(3)S△CC1C2=×3×6=9.
20. 解:如图.
(1)顺次连接点A、B、C、D得四边形ABCD;
(2)以点O为位似中心,把四边形ABCD放大两倍,得新四边形A1B1C1D1和四边形A2B2C2D2.
一、选择题
1.下列各组图形中,不是位似图形的是( )
2.如图中的两个三角形是位似图形,它们的位似中心是( )
A.点P B.点O C.点M D.点N
3.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是( )
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2∶3
C.四边形ABCD与四边形AEFG的周长比是2∶3
D.四边形ABCD与四边形AEFG的面积比是4∶9
4.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比值是( )
A. B. C. D.
5.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8)、B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1) B.(4,3) C.(3,4) D.(1,5)
6.如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-1,2) B.(-9,18) C.(-9,18)或(9,-18) D.(-1,2)或(1,-2)
7.如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,边OC在y轴上.如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于OABC的面积的,则点B的对应点B′的坐标为( )
A.(-2,3) B.(2,-3)
C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
8.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
9.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=8,则S△A′B′C′等于( )
A.15 B.16 C.17 D.18
二、填空题
10.在平面直角坐标系中,△ABC顶点A的坐标为(2,3),若以原点O为位似中心,画△AEC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比等于,则点A′的坐标为________.
11.如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是________.
12. 如图,点O是等边△PQR的中心,P′、Q′、R′分别是OP、OQ、OR的中点,则△P′Q′R′与△PQR是位似三角形,此时△P′Q′R′与△PQR的位似比为 、位似中心为 .
13. 如图所示,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,点A、B、A′、B′均在图中格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为 .
14. 在平面直角坐标系中,以原点O为位似中心,相似比为k(k>0)画位似图形,若原图上的点的坐标为(x,y),则位似图形对应点的坐标为 或 .
15. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是 .
16. 如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB∶FG=2∶3,3DE= MN.
三、解答题
17. 如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且相似比为1∶2;
(2)连接(1)中的AA′,求四边形AA′C′C的周长(结果保留根号).
18. 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心O;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1∶5.
19. 如图,在边长为1个单位长度的小正方形网格中.
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1;
(2)以B为位似中心,将△ABC放大为原来的2倍,得到△A2BC2,请在网格中画出△A2BC2;
(3)求△CC1C2的面积.
20. 如下图所示的平面直角坐标系中,
(1)描出下列各点:A(1,0)、B(3,0)、C(3,3)、D(0,1),并将这些点用线段依次连接起来;
(2)以坐标原点O为位似中心,把(1)中所得图形放大两倍.
答案:
一、
1-9 BABDC DDAD
二、
10. (4,6)或(-4,-6)
11. (-2,0)
12. 点O
13. (,)
14. (kx,ky) (-kx,-ky)
15. 1∶4
16. 2
三、
17. 解:(1)如图:
(2)四边形AA′C′C的周长=4+6.
18. 解:(1)略;
(2)1∶2;
(3)画图略,寻找A1、B1、C1的方法是===5即可.
19. 解:(1)(2)如图:
(3)S△CC1C2=×3×6=9.
20. 解:如图.
(1)顺次连接点A、B、C、D得四边形ABCD;
(2)以点O为位似中心,把四边形ABCD放大两倍,得新四边形A1B1C1D1和四边形A2B2C2D2.
