2021-2022学年鲁教版(五四制)八年级数学下册 6》2矩形的判定与性质 解答题专题提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册 6》2矩形的判定与性质 解答题专题提升训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 178.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 21:22:24 | ||
图片预览




文档简介
2021-2022学年鲁教版八年级数学下册《6-2矩形的判定与性质》
解答题专题提升训练(附答案)
1.如图,在矩形ABCD中,点E,F在对角线BD上,BE=DF.请你判断:AE与CF的关系,并加以证明,(友情提示:不要漏解!)
2.如图,已知矩形ABCD,对角线BD的垂直平分线分别交AD,BC和BD于点E,F,O.EF,DC的延长线交于点G,且OD=CG,连接BE.
(1)求证:△DOE≌△GCF;
(2)求证:BE平分∠ABD.
3.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.如图.
(1)∠BEC= °;
(2)在图中已有的三角形中,找到一对全等的三角形,并证明你的结论;
4.如图,矩形ABCD中,对角线AC与BD相交于点,过点A作AN∥BD,过点B作BN∥AC,两线相交于点N.
(1)求证:AN=BN;
(2)连接DN,交AC于点F,若DN⊥NB于点N,求∠DOC的度数.
5.如图,已知矩形ABCD中,E、F是AB上两点,且AF=DE,求证:∠DEB=∠CFA.
6.如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB于点O,若BC=8,AO=,求的值.
7.已知:如图,在矩形ABCD中,E为AD上一点,EF⊥CE,交AB于点F,DE=2,矩形的周长为16,且CE=EF.求AE的长.
8.如图,在 ABCD中,对角线AC,BD交于点O,且OA=OB.
(1)求证: ABCD是矩形;
(2)点E在BA延长线上,且AE=AB,连接DE,求证:DE=AC.
9.如图,矩形ABCD的对角线AC、BD交于点O,∠AOD=60°,AB=,AE⊥BD于点E,求OE的长.
10.已知:如图,四边形ABCD是矩形,∠ECD=∠DBA,∠CED=90°,AF⊥BD于点F.
(1)求证:四边形BCEF是平行四边形;
(2)若AB=4,AD=3,求EC的长.
11.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
12.如图,将平行四边形ABCD的边AB延长到点E,使BE=AB,DE交边BC于点F.
(1)求证:四边形BECD为平行四边形;
(2)连接BD、CE,若∠BFD=2∠A,求证:四边形BECD是矩形.
13.已知:如图,M为平行四边形ABCD边AD的中点,且MB=MC.求证:四边形ABCD是矩形.
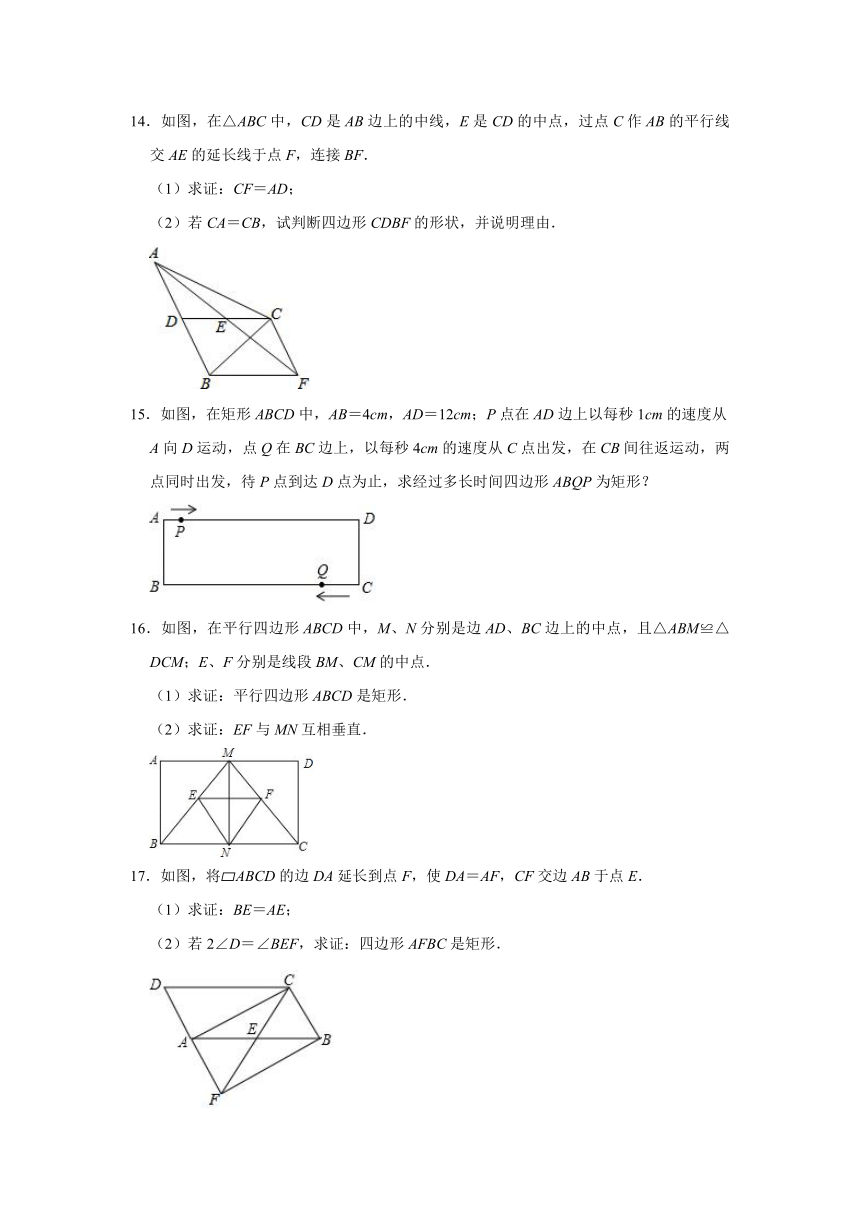
14.如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)求证:CF=AD;
(2)若CA=CB,试判断四边形CDBF的形状,并说明理由.
15.如图,在矩形ABCD中,AB=4cm,AD=12cm;P点在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,两点同时出发,待P点到达D点为止,求经过多长时间四边形ABQP为矩形?
16.如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.
17.如图,将 ABCD的边DA延长到点F,使DA=AF,CF交边AB于点E.
(1)求证:BE=AE;
(2)若2∠D=∠BEF,求证:四边形AFBC是矩形.
18.如图,四边形ABCD是平行四边形,点E在CB的延长线上,且BE=BC,DE=DC,AB、DE相交于点O,连接AE.求证:四边形AEBD是矩形.
19.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
20.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
21.如图,在 ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E.
(1)求证:四边形ACED是矩形;
(2)连接AE交CD于点F,连接BF.若∠ABC=60°,CE=2,求BF的长.
22.如图,在平行四边形ABCD中,AE⊥BC于E,点F在BC延长线上,且CF=BE,连接AC,DF.
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,CF=3,DF=4,求AD的长度.
23.已知:如图,点E为 ABCD对角线AC上的一点,点F在线段BE的延长线上,且EF=BE,线段EF与边CD相交于点G.
(1)求证:DF∥AC;
(2)如果AB=BE,DG=CG,联结DE、CF,求证:四边形DECF是矩形.
24.如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
参考答案
1.解:AE与CF相等且平行;或相等且共线.理由如下:
(1)数量关系:AE=CF.理由如下:
∵四边形ABCD是矩形,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
∴AE=CF.
(2)当点E与点F不在BD的中点时,AE∥FC.
∵△ABE≌△CDF,
∴∠AEB=∠CFD,
∴∠AED=∠CFB,
∴AE∥CF.
(3)当点E和点F在BD的中点时,AE与CF共线.
2.证明:(1)∵EF是BD垂直平分线,
∴∠EOD=90°,
在矩形ABCD中,AD∥BC,∠A=∠BCD=90°,
∴∠DEO=∠GFC,∠DEO=∠BFO,∠FCG=90°,
∴∠EOD=∠FCG,
在△DOE和△GCF中,,
∴△DOE≌△GCF(AAS);
(2)由(1)得:△DOE≌GCF,
∴OE=CF,
∵EF是BD垂直平分线,
∴OB=OD,
在△DOE和△BOF中,,
∴△DOE≌△BOF(AAS),
∴DE=BF,
∵AD=BC,
∴AE=CF=OE,
∴BE平分∠ABD.
3.解:(1)∵四边形ABCD为矩形,
∴∠ABC=∠BCD=90°,
∵BE平分∠ABC,
∴∠EBC=45°,
∴∠BEC=45°,
故答案为:45;
(2)△ADE≌△ECF,理由如下:
∵四边形ABCD是矩形,
∴∠ABC=∠C=∠D=90°,AD=BC.
∵FE⊥AE,
∴∠AEF=90°.
∴∠AED+∠FEC=180°﹣∠AEF=90°.
∵∠AED+∠DAE=90°,
∴∠FEC=∠EAD,
∵BE平分∠ABC,
∴∠EBC=∠ABC=45°.
∴∠BEC=45°.
∴∠EBC=∠BEC.
∴BC=EC.
∴AD=EC.
在△ADE和△ECF中,,
∴△ADE≌△ECF(ASA).
4.解:(1)证明:∵矩形ABCD中,对角线AC与BD相交于点O,
∴OA=OB,
∵AN∥BD,BN∥AC,
∴四边形OANB是平行四边形,
∵OA=OB,
∴ OANB是菱形,
∴AN=BN,
(2)由(1)可知:
BN=OB=OD,
∴BD=2BN,
∵DN⊥NB,
∴∠DNB=90°,
∴∠BDN=30°,
∵BN∥AC,
∴∠DFO=∠DNB=90°,
∴∠DOF=90°﹣30°=60°,
∴∠DOC=180°﹣60°=120°.
答:∠DOC的度数为120°.
5.证明:∵ABCD为矩形,
∴AB=CD,∠A=∠D.
∵AF=DE,
∴AE=DF.
∴△ABE≌△DCF.
∴∠AEB=∠DFC.
∴∠DEB=∠CFA.
6.(1)证明:∵AE∥BC,BE∥AD,
∴四边形ADBE是平行四边形.
∵AB=AC,AD是BC边的中线,
∴AD⊥BC.
即∠ADB=90°.
∴四边形ADBE为矩形.
(2)解:∵在矩形ADBE中,AO=,
∴DE=AB=5.
∵D是BC的中点,BC=8,
∴AE=DB=4,
∴.
7.解:∵四边形ABCD为矩形,
∴∠A=∠D=90°
∵EF⊥CE
∴∠CEF=90°
∴∠CED+∠AEF=90°
∵∠CED+∠DCE=90°
∴∠DCE=∠AEF
∵CE=EF,∠A=∠D,∠DCE=∠AEF
∴△AEF≌△DCE
∴AE=DC
由题意可知:2(AE+DE+CD)=16 且DE=2
∴2AE=6
∴AE=3
8.(1)证明:在 ABCD中,OA=OC=AC,OB=OD=BD,
又∵OA=OB,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)∵ ABCD是矩形,
∴CD=AB,CD∥BE,
∵AE=AB,
∴CD=AE,
∴四边形ACDE是平行四边形,
∴DE=AC.
9.解:∵对角线相等且互相平分,
∴OA=OD
∵∠AOD=60°
∴△AOD为等边三角形,则OA=AD,
BD=2DO,AB=AD,
∴AD=2,
∵AE⊥BD,∴E为OD的中点
∴OE=OD=AD=1,
答:OE的长度为 1.
10.(1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,DC=AB,DC∥AB,
∴∠CDF=∠DBA.
∵∠ECD=∠DBA,
∴∠ECD=∠CDF,
∴EC∥BF,
∵AF⊥BD于点F,∠CED=90°,
∴∠BFA=∠CED=90°.
在△ECD和△FBA中,,
∴△ECD≌△FBA(AAS),
∴EC=BF,
又∵EC∥BF,
∴四边形BCEF是平行四边形;
(2)解:∵AB=4,AD=3,
∴BD==5,
∵AF⊥BD,
∴∠AFB=90°=∠BAD,
∵∠ABF=∠ABD,
∴,
∴EC=BF=.
11.解:(1)OE=OF,理由如下:
∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠ECB,
∴∠OEC=∠ACE,
∴OE=OC,
同理可得:OC=OF,
∴OE=OF;
(2)当O为AC中点时,四边形AECF是矩形;
理由如下:
∵OA=OC,OE=OF(已证),
∴四边形AECF是平行四边形,
∵EC平分∠ACB,CF平分∠ACG,
∴∠ACE=∠ACB,∠ACF=∠ACG,
∴∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
即∠ECF=90°,
∴四边形AECF是矩形.
12.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=AB,
∴BE=CD,
∴四边形BECD为平行四边形;
(2)∵四边形ABCD是平行四边形,
∴∠A=∠DCB,
∵∠BFD=2∠A,
∴∠BFD=2∠DCB,
∴∠DCF=∠FDC,
∴DF=CF,
由(1)得:四边形BECD为平行四边形,
∴EF=DF,BF=CF,
∴DE=BC,
∴四边形BECD是矩形.
13.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠A+∠D=180°,
在△ABM和△DCM中,
,
∴△ABM≌△DCM(SSS),
∴∠A=∠D=90°,
即可得出平行四边形ABCD是矩形.
14.证明:(1)∵AB∥CF
∴∠EAD=∠EFC,∠ADE=∠FCE,
∵E是CD的中点,∴DE=CE
在△ADE和△FCE中,
,
∴△ADE≌FCE
∴AD=CF
(2)结论:边形CDBF是矩形.
理由:∵AD=CF
∵CD是AB边上的中线
∴AD=BD
∴BD=CF
又∵BD∥CF
∴四边形CDBF是平行四边形
∵CA=CB,AD=BD,
∴CD⊥AB,
∴∠CDB=90°
∴四边形CDBF是矩形.﹣
15.解:∵在矩形ABCD中,AD=12cm,
∴AD=BC=12cm.
当四边形ABQP为矩形时,AP=BQ.
①当0<t<3时,t=12﹣4t,
解得,t=;
②当3≤t<6时,t=4t﹣12,
解得 t=4;
③当6≤t<9时,t=36﹣4t,
解得 t=;
④当9≤t≤12时,t=4t﹣36,
解得,t=12.
综上所述,当t为或4或或12时,四边形ABQP为矩形.
16.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠A+∠D=180°,
又∵△ABM≌△DCM,
∴∠A=∠D=90°,
∴平行四边形ABCD是矩形.
(2)证明:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,NE=CM,MF=CM.
∴NE=FM,NE∥FM.
∴四边形MENF是平行四边形.
∵△ABM≌△DCM,
∴BM=CM.
∵E、F分别是BM、CM的中点,
∴ME=MF.
∴平行四边形MENF是菱形.
∴EF与MN互相垂直.
17.证明:(1)∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC
∵DA=AF
∴AF=BC,且AD∥BC
∴四边形ACBF是平行四边形
∴BE=AE,
(2)∵四边形ABCD是平行四边形
∴∠D=∠ABC
∵2∠D=∠BEF,且∠BEF=∠ABC+∠ECB
∴2∠ABC=∠ABC+∠ECB
∴∠ECB=∠ABC
∴CE=BE
∵四边形ACBF是平行四边形
∴AE=BE,CE=EF
∴AB=CF,且四边形ACBF是平行四边形
∴平行四边形ACBF是矩形.
18.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,CD=AB,
∵BC=BE,
∴AD=BE,AD∥BE,
∴四边形AEBD是平行四边形,
∵DE=DC,
∴AB=ED,
∴平行四边形ADBE是矩形.
19.证明:
(1)∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
,
∴△AEF≌△DEC(AAS),
∴AF=DC,
∵AF=BD,
∴BD=CD;
(2)四边形AFBD是矩形.
理由:∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°
∵AF=BD,
∵过A点作BC的平行线交CE的延长线于点F,即AF∥BC,
∴四边形AFBD是平行四边形,
又∵∠ADB=90°,
∴四边形AFBD是矩形.
20.证明:∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AC=2AO,BD=2OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠CAD=∠ACB=90°.
又∵∠ACE=90°,DE⊥BC,
∴四边形ACED是矩形.
(2)解:∵四边形ACED是矩形,
∴AD=CE=2,AF=EF,AE=CD.
∵四边形ABCD是平行四边形,
∴BC=AD=2,AB=CD.
∴AB=AE.
又∵∠ABC=60°,
∴△ABE是等边三角形.
∴∠BFE=90°,.
在Rt△BFE中,.
22.(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
∵在 ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)解:∵四边形AEFD是矩形,
∴AE=DF=5,∠AEC=∠F=90°,
∵∠ACD=90°,
∴∠EAC+∠ACE=∠ACE+∠DCF=90°,
∴∠EAC=∠DCF,
∴CE=,
∴EF=CE+CF=,
∵四边形AEFD是矩形,
∴AD=EF=.
23.(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,
∵EF=BE,
∴OE是△BDF的中位线,
∴OE∥DF,
即DF∥AC;
(2)解:∵AB=BE,
∴∠BAE=∠BEA,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠GCE,
∵∠BEA=∠GEC,
∴∠GEC=∠GCE,
∴GE=CG,
∵DF∥AC,
∵DG=CG,
∴FG=GE,
∴四边形DECF是平行四边形,
∵DG=CG,FG=GE,GE=CG,
∴DG=CG=FG=GE,
∴DC=EF,
∴四边形DECF是矩形.
24.(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.
解答题专题提升训练(附答案)
1.如图,在矩形ABCD中,点E,F在对角线BD上,BE=DF.请你判断:AE与CF的关系,并加以证明,(友情提示:不要漏解!)
2.如图,已知矩形ABCD,对角线BD的垂直平分线分别交AD,BC和BD于点E,F,O.EF,DC的延长线交于点G,且OD=CG,连接BE.
(1)求证:△DOE≌△GCF;
(2)求证:BE平分∠ABD.
3.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.如图.
(1)∠BEC= °;
(2)在图中已有的三角形中,找到一对全等的三角形,并证明你的结论;
4.如图,矩形ABCD中,对角线AC与BD相交于点,过点A作AN∥BD,过点B作BN∥AC,两线相交于点N.
(1)求证:AN=BN;
(2)连接DN,交AC于点F,若DN⊥NB于点N,求∠DOC的度数.
5.如图,已知矩形ABCD中,E、F是AB上两点,且AF=DE,求证:∠DEB=∠CFA.
6.如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB于点O,若BC=8,AO=,求的值.
7.已知:如图,在矩形ABCD中,E为AD上一点,EF⊥CE,交AB于点F,DE=2,矩形的周长为16,且CE=EF.求AE的长.
8.如图,在 ABCD中,对角线AC,BD交于点O,且OA=OB.
(1)求证: ABCD是矩形;
(2)点E在BA延长线上,且AE=AB,连接DE,求证:DE=AC.
9.如图,矩形ABCD的对角线AC、BD交于点O,∠AOD=60°,AB=,AE⊥BD于点E,求OE的长.
10.已知:如图,四边形ABCD是矩形,∠ECD=∠DBA,∠CED=90°,AF⊥BD于点F.
(1)求证:四边形BCEF是平行四边形;
(2)若AB=4,AD=3,求EC的长.
11.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
12.如图,将平行四边形ABCD的边AB延长到点E,使BE=AB,DE交边BC于点F.
(1)求证:四边形BECD为平行四边形;
(2)连接BD、CE,若∠BFD=2∠A,求证:四边形BECD是矩形.
13.已知:如图,M为平行四边形ABCD边AD的中点,且MB=MC.求证:四边形ABCD是矩形.
14.如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)求证:CF=AD;
(2)若CA=CB,试判断四边形CDBF的形状,并说明理由.
15.如图,在矩形ABCD中,AB=4cm,AD=12cm;P点在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,两点同时出发,待P点到达D点为止,求经过多长时间四边形ABQP为矩形?
16.如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.
17.如图,将 ABCD的边DA延长到点F,使DA=AF,CF交边AB于点E.
(1)求证:BE=AE;
(2)若2∠D=∠BEF,求证:四边形AFBC是矩形.
18.如图,四边形ABCD是平行四边形,点E在CB的延长线上,且BE=BC,DE=DC,AB、DE相交于点O,连接AE.求证:四边形AEBD是矩形.
19.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
20.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
21.如图,在 ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E.
(1)求证:四边形ACED是矩形;
(2)连接AE交CD于点F,连接BF.若∠ABC=60°,CE=2,求BF的长.
22.如图,在平行四边形ABCD中,AE⊥BC于E,点F在BC延长线上,且CF=BE,连接AC,DF.
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,CF=3,DF=4,求AD的长度.
23.已知:如图,点E为 ABCD对角线AC上的一点,点F在线段BE的延长线上,且EF=BE,线段EF与边CD相交于点G.
(1)求证:DF∥AC;
(2)如果AB=BE,DG=CG,联结DE、CF,求证:四边形DECF是矩形.
24.如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
参考答案
1.解:AE与CF相等且平行;或相等且共线.理由如下:
(1)数量关系:AE=CF.理由如下:
∵四边形ABCD是矩形,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
∴AE=CF.
(2)当点E与点F不在BD的中点时,AE∥FC.
∵△ABE≌△CDF,
∴∠AEB=∠CFD,
∴∠AED=∠CFB,
∴AE∥CF.
(3)当点E和点F在BD的中点时,AE与CF共线.
2.证明:(1)∵EF是BD垂直平分线,
∴∠EOD=90°,
在矩形ABCD中,AD∥BC,∠A=∠BCD=90°,
∴∠DEO=∠GFC,∠DEO=∠BFO,∠FCG=90°,
∴∠EOD=∠FCG,
在△DOE和△GCF中,,
∴△DOE≌△GCF(AAS);
(2)由(1)得:△DOE≌GCF,
∴OE=CF,
∵EF是BD垂直平分线,
∴OB=OD,
在△DOE和△BOF中,,
∴△DOE≌△BOF(AAS),
∴DE=BF,
∵AD=BC,
∴AE=CF=OE,
∴BE平分∠ABD.
3.解:(1)∵四边形ABCD为矩形,
∴∠ABC=∠BCD=90°,
∵BE平分∠ABC,
∴∠EBC=45°,
∴∠BEC=45°,
故答案为:45;
(2)△ADE≌△ECF,理由如下:
∵四边形ABCD是矩形,
∴∠ABC=∠C=∠D=90°,AD=BC.
∵FE⊥AE,
∴∠AEF=90°.
∴∠AED+∠FEC=180°﹣∠AEF=90°.
∵∠AED+∠DAE=90°,
∴∠FEC=∠EAD,
∵BE平分∠ABC,
∴∠EBC=∠ABC=45°.
∴∠BEC=45°.
∴∠EBC=∠BEC.
∴BC=EC.
∴AD=EC.
在△ADE和△ECF中,,
∴△ADE≌△ECF(ASA).
4.解:(1)证明:∵矩形ABCD中,对角线AC与BD相交于点O,
∴OA=OB,
∵AN∥BD,BN∥AC,
∴四边形OANB是平行四边形,
∵OA=OB,
∴ OANB是菱形,
∴AN=BN,
(2)由(1)可知:
BN=OB=OD,
∴BD=2BN,
∵DN⊥NB,
∴∠DNB=90°,
∴∠BDN=30°,
∵BN∥AC,
∴∠DFO=∠DNB=90°,
∴∠DOF=90°﹣30°=60°,
∴∠DOC=180°﹣60°=120°.
答:∠DOC的度数为120°.
5.证明:∵ABCD为矩形,
∴AB=CD,∠A=∠D.
∵AF=DE,
∴AE=DF.
∴△ABE≌△DCF.
∴∠AEB=∠DFC.
∴∠DEB=∠CFA.
6.(1)证明:∵AE∥BC,BE∥AD,
∴四边形ADBE是平行四边形.
∵AB=AC,AD是BC边的中线,
∴AD⊥BC.
即∠ADB=90°.
∴四边形ADBE为矩形.
(2)解:∵在矩形ADBE中,AO=,
∴DE=AB=5.
∵D是BC的中点,BC=8,
∴AE=DB=4,
∴.
7.解:∵四边形ABCD为矩形,
∴∠A=∠D=90°
∵EF⊥CE
∴∠CEF=90°
∴∠CED+∠AEF=90°
∵∠CED+∠DCE=90°
∴∠DCE=∠AEF
∵CE=EF,∠A=∠D,∠DCE=∠AEF
∴△AEF≌△DCE
∴AE=DC
由题意可知:2(AE+DE+CD)=16 且DE=2
∴2AE=6
∴AE=3
8.(1)证明:在 ABCD中,OA=OC=AC,OB=OD=BD,
又∵OA=OB,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)∵ ABCD是矩形,
∴CD=AB,CD∥BE,
∵AE=AB,
∴CD=AE,
∴四边形ACDE是平行四边形,
∴DE=AC.
9.解:∵对角线相等且互相平分,
∴OA=OD
∵∠AOD=60°
∴△AOD为等边三角形,则OA=AD,
BD=2DO,AB=AD,
∴AD=2,
∵AE⊥BD,∴E为OD的中点
∴OE=OD=AD=1,
答:OE的长度为 1.
10.(1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,DC=AB,DC∥AB,
∴∠CDF=∠DBA.
∵∠ECD=∠DBA,
∴∠ECD=∠CDF,
∴EC∥BF,
∵AF⊥BD于点F,∠CED=90°,
∴∠BFA=∠CED=90°.
在△ECD和△FBA中,,
∴△ECD≌△FBA(AAS),
∴EC=BF,
又∵EC∥BF,
∴四边形BCEF是平行四边形;
(2)解:∵AB=4,AD=3,
∴BD==5,
∵AF⊥BD,
∴∠AFB=90°=∠BAD,
∵∠ABF=∠ABD,
∴,
∴EC=BF=.
11.解:(1)OE=OF,理由如下:
∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠ECB,
∴∠OEC=∠ACE,
∴OE=OC,
同理可得:OC=OF,
∴OE=OF;
(2)当O为AC中点时,四边形AECF是矩形;
理由如下:
∵OA=OC,OE=OF(已证),
∴四边形AECF是平行四边形,
∵EC平分∠ACB,CF平分∠ACG,
∴∠ACE=∠ACB,∠ACF=∠ACG,
∴∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
即∠ECF=90°,
∴四边形AECF是矩形.
12.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=AB,
∴BE=CD,
∴四边形BECD为平行四边形;
(2)∵四边形ABCD是平行四边形,
∴∠A=∠DCB,
∵∠BFD=2∠A,
∴∠BFD=2∠DCB,
∴∠DCF=∠FDC,
∴DF=CF,
由(1)得:四边形BECD为平行四边形,
∴EF=DF,BF=CF,
∴DE=BC,
∴四边形BECD是矩形.
13.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠A+∠D=180°,
在△ABM和△DCM中,
,
∴△ABM≌△DCM(SSS),
∴∠A=∠D=90°,
即可得出平行四边形ABCD是矩形.
14.证明:(1)∵AB∥CF
∴∠EAD=∠EFC,∠ADE=∠FCE,
∵E是CD的中点,∴DE=CE
在△ADE和△FCE中,
,
∴△ADE≌FCE
∴AD=CF
(2)结论:边形CDBF是矩形.
理由:∵AD=CF
∵CD是AB边上的中线
∴AD=BD
∴BD=CF
又∵BD∥CF
∴四边形CDBF是平行四边形
∵CA=CB,AD=BD,
∴CD⊥AB,
∴∠CDB=90°
∴四边形CDBF是矩形.﹣
15.解:∵在矩形ABCD中,AD=12cm,
∴AD=BC=12cm.
当四边形ABQP为矩形时,AP=BQ.
①当0<t<3时,t=12﹣4t,
解得,t=;
②当3≤t<6时,t=4t﹣12,
解得 t=4;
③当6≤t<9时,t=36﹣4t,
解得 t=;
④当9≤t≤12时,t=4t﹣36,
解得,t=12.
综上所述,当t为或4或或12时,四边形ABQP为矩形.
16.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠A+∠D=180°,
又∵△ABM≌△DCM,
∴∠A=∠D=90°,
∴平行四边形ABCD是矩形.
(2)证明:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,NE=CM,MF=CM.
∴NE=FM,NE∥FM.
∴四边形MENF是平行四边形.
∵△ABM≌△DCM,
∴BM=CM.
∵E、F分别是BM、CM的中点,
∴ME=MF.
∴平行四边形MENF是菱形.
∴EF与MN互相垂直.
17.证明:(1)∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC
∵DA=AF
∴AF=BC,且AD∥BC
∴四边形ACBF是平行四边形
∴BE=AE,
(2)∵四边形ABCD是平行四边形
∴∠D=∠ABC
∵2∠D=∠BEF,且∠BEF=∠ABC+∠ECB
∴2∠ABC=∠ABC+∠ECB
∴∠ECB=∠ABC
∴CE=BE
∵四边形ACBF是平行四边形
∴AE=BE,CE=EF
∴AB=CF,且四边形ACBF是平行四边形
∴平行四边形ACBF是矩形.
18.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,CD=AB,
∵BC=BE,
∴AD=BE,AD∥BE,
∴四边形AEBD是平行四边形,
∵DE=DC,
∴AB=ED,
∴平行四边形ADBE是矩形.
19.证明:
(1)∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
,
∴△AEF≌△DEC(AAS),
∴AF=DC,
∵AF=BD,
∴BD=CD;
(2)四边形AFBD是矩形.
理由:∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°
∵AF=BD,
∵过A点作BC的平行线交CE的延长线于点F,即AF∥BC,
∴四边形AFBD是平行四边形,
又∵∠ADB=90°,
∴四边形AFBD是矩形.
20.证明:∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AC=2AO,BD=2OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠CAD=∠ACB=90°.
又∵∠ACE=90°,DE⊥BC,
∴四边形ACED是矩形.
(2)解:∵四边形ACED是矩形,
∴AD=CE=2,AF=EF,AE=CD.
∵四边形ABCD是平行四边形,
∴BC=AD=2,AB=CD.
∴AB=AE.
又∵∠ABC=60°,
∴△ABE是等边三角形.
∴∠BFE=90°,.
在Rt△BFE中,.
22.(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
∵在 ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)解:∵四边形AEFD是矩形,
∴AE=DF=5,∠AEC=∠F=90°,
∵∠ACD=90°,
∴∠EAC+∠ACE=∠ACE+∠DCF=90°,
∴∠EAC=∠DCF,
∴CE=,
∴EF=CE+CF=,
∵四边形AEFD是矩形,
∴AD=EF=.
23.(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,
∵EF=BE,
∴OE是△BDF的中位线,
∴OE∥DF,
即DF∥AC;
(2)解:∵AB=BE,
∴∠BAE=∠BEA,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠GCE,
∵∠BEA=∠GEC,
∴∠GEC=∠GCE,
∴GE=CG,
∵DF∥AC,
∵DG=CG,
∴FG=GE,
∴四边形DECF是平行四边形,
∵DG=CG,FG=GE,GE=CG,
∴DG=CG=FG=GE,
∴DC=EF,
∴四边形DECF是矩形.
24.(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.
