2021-2022学年人教版七年级数学下册5.3.1平行线的性质与判定专项测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.3.1平行线的性质与判定专项测试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 412.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 00:00:00 | ||
图片预览




文档简介
2022七年级数学下平行线的性质与判定专项测试卷
满分:120分 完成时间60分钟 姓名
题号 一 二 三 总分
得分
一、单选题
1.(2021·广东·深圳市南山外国语学校(集团)七年级期中)下列说法:
①在同一平面内,不相交的两条线段叫做平行线;
②过一点,有且只有一条直线平行于已知直线;
③两条平行直线被第三条直线所截,同位角相等;
④同旁内角相等,两直线平行.
正确的个数有( )个.
A.1 B.2 C.3 D.4
2.(2021·江苏·开明中学九年级期末)如图,直线a∥b,直线AB⊥AC,若∠1=52°,则∠2的度数是( )
A.38° B.42° C.48° D.52°
3.(2022·辽宁铁西·八年级期末)一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=( )
A.62° B.58° C.52° D.48°
第2题图 第3题图 第4题图 第5题图
4.(2018·浙江衢州·中考真题)如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110° C.108° D.106°
5.(2019·山东济南·中考真题)如图,,平分,若,则的度数为( )
A. B. C. D.
6.(2020·山东枣庄·中考真题)一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
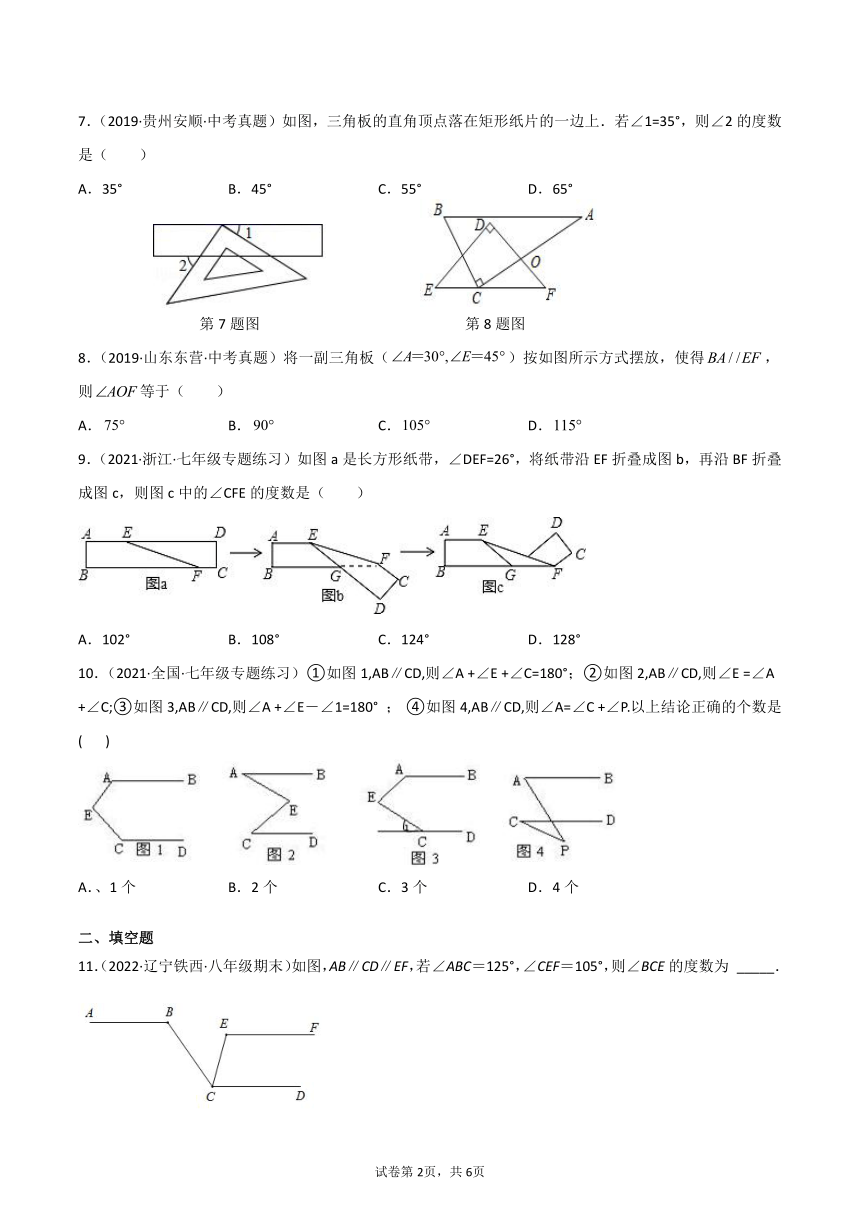
7.(2019·贵州安顺·中考真题)如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.65°
第7题图 第8题图
8.(2019·山东东营·中考真题)将一副三角板()按如图所示方式摆放,使得,则等于( )
A. B. C. D.
9.(2021·浙江·七年级专题练习)如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.102° B.108° C.124° D.128°
10.(2021·全国·七年级专题练习)①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A.、1个 B.2个 C.3个 D.4个
二、填空题
11.(2022·辽宁铁西·八年级期末)如图,AB∥CD∥EF,若∠ABC=125°,∠CEF=105°,则∠BCE的度数为 _____.
12.(2020·福建·莆田第七中学八年级阶段练习)如图所示,直线a∥b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠l=58°,则∠2= ___________ .
第12题图 第13题图 第14题图
13.(2011·广西贵港·中考真题)如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=____.
14.(2021·全国·七年级专题练习)如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.有下列结论:①∠BOE=(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是________(填序号).
15.(2021·全国·七年级专题练习)观察下列图形:已知在第一个图中,可得∠1+∠2=180°,则按照以上规律:_________度.
三、解答题
16.(2022·河南·驻马店市第二初级中学八年级期末)请把下列证明过程及理由补充完整(填在横线上):
已知:如图,BC,AF是直线,AD∥BC,∠1=∠2,∠3=∠4.求证:AB∥CD.
证明:∵AD∥BC(已知),
∴∠3= ( ).
∵∠3=∠4(已知),
∴∠4= ( ).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF( ).
即∠BAF= .
∴∠4=∠BAF.( ).
∴AB∥CD( ).
17.(2022·四川省遂宁市第二中学校七年级期末)如图,已知∠A=120°,∠FEC=120°,∠1=∠2,试说明∠FDG=∠EFD.请补全证明过程,即在下列括号内填上结论或理由.
解:∵∠A=120°,∠FEC=120°(已知),
∴∠A= ( ).
∴AB∥ ( ).
又∵∠1=∠2(已知),
∴AB∥CD ( ).
∴EF∥ ( ).
∴∠FDG=∠EFD ( ).
18.(2022·吉林·长春外国语学校七年级期末)阅读下面的推理过程,将空白部分补充完整.
已知:如图,在△ABC中,FGCD,∠1 = ∠3.
求证:∠B + ∠BDE= 180°.
解:因为FGCD(已知),
所以∠1= .
又因为∠1 = ∠3 (已知),
所以∠2 = (等量代换).
所以BC ( ),
所以∠B + ∠BDE = 180°(___________________).
19.(2021·河南灵宝·七年级期中)如图,已知∠1+∠2=180°,∠3=∠B,求证:DE∥BC.
20.(2021·贵州碧江·七年级期末)如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
21.(2021·全国·七年级专题练习)如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D,
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
22.(2019·广西港南·七年级期末)已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
23.(2017·北京东城·七年级期中)已知:直线,点、分别在直线,上,点为平面内一点.
()如图,,,的数量关系是__________.
()利用()的结论解决问题:如图,已知,平分,平分,,求得度数.
()如图,点为上一点,,,交于点,直接写出,,之间的数量关系.(用含的式子表示)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A【解析】
①在同一平面内,不相交的两条直线叫做平行线,故原命题错误;
②过直线外一点,有且只有一条直线平行于已知直线,故原命题错误;
③两条平行直线被第三条直线所截,同位角相等,正确;
④同旁内角互补,两直线平行,故原命题错误.
故选:A
2.A【解】
解:∵AB⊥AC,∠1=52°,
∴∠B=90°﹣∠1
=90°﹣52°
=38°
∵a∥b,
∴∠2=∠B=38°.
故选:A.
3.A【详解】
解:如图,过三角板的直角顶点作直尺两边的平行线,
∵直尺的两边互相平行,
∴,
∴,
∴,
4.D【详解】
分析:由折叠可得:∠DGH=∠DGE=74°,再根据AD∥BC,即可得到∠GHC=180°﹣∠DGH=106°.
详解:∵∠AGE=32°,
∴∠DGE=148°,
由折叠可得:∠DGH=∠DGE=74°.
∵AD∥BC,
∴∠GHC=180°﹣∠DGH=106°.
故选D.
5.B【详解】
∵,
∴,
∵平分,
∴,
故选B.
6.B【详解】
由题意可得:∠EDF=45°,∠ABC=30°,
∵AB∥CF,
∴∠ABD=∠EDF=45°,
∴∠DBC=45°﹣30°=15°.
故选B.
7.C【详解】
分析:求出∠3即可解决问题;
详解:如图,
∵∠1+∠3=90°,∠1=35°,
∴∠3=55°,
∴∠2=∠3=55°,
故选C.
8.A【详解】
解:,
.
,
.
故选.
9.A【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFE=∠DEF=26°,
∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°,
故选A.
10.C【详解】
①如图1,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A+∠AEF=180°,∠C+∠CEF=180°,
所以∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°,则①错误;
②如图2,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A=∠AEF,∠C=∠CEF,
所以∠A+∠C=∠AEC+∠AEF=∠AEC,则②正确;
③如图3,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A+∠AEF=180°,∠1=∠CEF,所以∠A+∠AEC-∠1=∠A+∠AEC-∠CEF=∠A+∠AEF=180°,则③正确;
④如图4,过点P作PF∥AB,因为AB∥CD,所以AB∥PF∥CD,
所以∠A=∠APF,∠C=∠CPF,所以∠A=∠CPF+∠APC=∠C+∠APC,则④正确;
故选C.
11.50°【详解】
解:∵AB∥CD∥EF,
∴∠BCD=∠ABC=125°,∠CEF+∠ECD=180°,
∴∠ECD=180°-∠CEF=75°,
∴∠BCE=∠BCD-∠ECD=50°,
故答案为:50°.
12.32°【详解】
∵直线a∥b,AM⊥b,
∴AM⊥a;
∴∠2=180°-90°-∠1;
∵∠1=58°,
∴∠2=32°.
故答案是:32°.
13.54°【详解】
∵AB∥CD,
∴∠BEF=180° ∠1=180° 72°=108°
∠2=∠BEG,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°
∴∠2=∠BEG=54°.
故答案为54°.
14.①②③【详解】
①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣(180﹣a)°=a°,
∴∠BOF=∠BOD,
∴OF平分∠BOD所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=a°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=a°,所以④错误.
故答案为①②③.
15.(n+1)×180【详解】
解:如图,分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,
∵AB∥CD,
∴AB∥P1E∥P2F∥P3G.
由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°
∴(1)∠1+∠2=180°,
(2)∠1+∠P1+∠2=2×180,
(3)∠1+∠P1+∠P2+∠2=3×180°,
(4)∠1+∠P1+∠P2+∠P3+∠2=4×180°,
∴∠1+∠2+∠P1+…+∠Pn=(n+1)×180°.
故答案为:(n+1)×180.
16.【详解】
证明:∵AD∥BC(已知),
∴∠3=∠CAD(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠4=∠CAD(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质).
即∠BAF=∠CAD.
∴∠4=∠BAF.(等量代换).
∴AB∥CD(同位角相等,两直线平行).
17.【详解】
解:∵∠A=120°,∠FEC=120°(已知),
∴∠A=∠FEC(等量代换),
∴AB∥EF(同位角相等,两直线平行),
又∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
∴EF∥CD(平行于同一条直线的两直线互相平行),
∴∠FDG=∠EFD(两直线平行,内错角相等),
故答案为:∠FEC;等量代换;EF;同位角相等,两直线平行;内错角相等,两直线平行;CD;平行于同一条直线的两直线互相平行;两直线平行,内错角相等.
18.【详解】
解:因为FGCD(已知),
所以∠1=∠2.
又因为∠1 = ∠3 (已知),
所以∠2 =∠3(等量代换).
所以(内错角相等,两直线平行),
所以∠B + ∠BDE = 180°(两直线平行,同旁内角互补).
故答案为:∠2;∠3;DE;内错角相等,两直线平行;两直线平行,同旁内角互补.
19.【详解】
要证明DE∥BC.需证明∠3=∠EHC.而证明∠3=∠EHC可通过证明EF∥AB及已知条件∠3=∠B进行推理即可.
证明:∵∠1+∠2=180°,∠1=∠4,
∴∠2+∠4=180°.
∴EH∥AB.
∴∠B=∠EHC.
∵∠3=∠B,
∴∠3=∠EHC.
∴DE∥BC.
20.【详解】
证明:如图,设BC与AE、GF分别交于点M、N.
∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNB=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
21.【详解】
解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,
故答案为60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,即∠APB:∠ADB=2:1.
22.【详解】
(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)不成立
如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
23.
【解析】
整体分析:
(1)过作,结合平行公理和平行线的性质即可得到,,的数量关系;(2)直接利用(1)中的结论,结合角平分线的定义及平行线的性质即可;(3)利用平行线的性质和角平分线的定义及角的和差关系建立之间的数量关系.
解:()过作.
∵,
∴,
∴,,
∴
,
即:.
()∵平分,平分,
∴,,
∵,由()结论可知,
∴
,
∴
.
∵,
∴,
又∵
,
∴,
∴.
(),,之间的数量关系是.
∵,,
∴,,
∵,
∴,
∵
,
∴,
∵,
∴,
∴,
∴.
逆 袭 卷
满分:120分 完成时间60分钟 姓名
题号 一 二 三 总分
得分
一、单选题
1.(2021·广东·深圳市南山外国语学校(集团)七年级期中)下列说法:
①在同一平面内,不相交的两条线段叫做平行线;
②过一点,有且只有一条直线平行于已知直线;
③两条平行直线被第三条直线所截,同位角相等;
④同旁内角相等,两直线平行.
正确的个数有( )个.
A.1 B.2 C.3 D.4
2.(2021·江苏·开明中学九年级期末)如图,直线a∥b,直线AB⊥AC,若∠1=52°,则∠2的度数是( )
A.38° B.42° C.48° D.52°
3.(2022·辽宁铁西·八年级期末)一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=( )
A.62° B.58° C.52° D.48°
第2题图 第3题图 第4题图 第5题图
4.(2018·浙江衢州·中考真题)如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110° C.108° D.106°
5.(2019·山东济南·中考真题)如图,,平分,若,则的度数为( )
A. B. C. D.
6.(2020·山东枣庄·中考真题)一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
7.(2019·贵州安顺·中考真题)如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.65°
第7题图 第8题图
8.(2019·山东东营·中考真题)将一副三角板()按如图所示方式摆放,使得,则等于( )
A. B. C. D.
9.(2021·浙江·七年级专题练习)如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.102° B.108° C.124° D.128°
10.(2021·全国·七年级专题练习)①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A.、1个 B.2个 C.3个 D.4个
二、填空题
11.(2022·辽宁铁西·八年级期末)如图,AB∥CD∥EF,若∠ABC=125°,∠CEF=105°,则∠BCE的度数为 _____.
12.(2020·福建·莆田第七中学八年级阶段练习)如图所示,直线a∥b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠l=58°,则∠2= ___________ .
第12题图 第13题图 第14题图
13.(2011·广西贵港·中考真题)如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=____.
14.(2021·全国·七年级专题练习)如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.有下列结论:①∠BOE=(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是________(填序号).
15.(2021·全国·七年级专题练习)观察下列图形:已知在第一个图中,可得∠1+∠2=180°,则按照以上规律:_________度.
三、解答题
16.(2022·河南·驻马店市第二初级中学八年级期末)请把下列证明过程及理由补充完整(填在横线上):
已知:如图,BC,AF是直线,AD∥BC,∠1=∠2,∠3=∠4.求证:AB∥CD.
证明:∵AD∥BC(已知),
∴∠3= ( ).
∵∠3=∠4(已知),
∴∠4= ( ).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF( ).
即∠BAF= .
∴∠4=∠BAF.( ).
∴AB∥CD( ).
17.(2022·四川省遂宁市第二中学校七年级期末)如图,已知∠A=120°,∠FEC=120°,∠1=∠2,试说明∠FDG=∠EFD.请补全证明过程,即在下列括号内填上结论或理由.
解:∵∠A=120°,∠FEC=120°(已知),
∴∠A= ( ).
∴AB∥ ( ).
又∵∠1=∠2(已知),
∴AB∥CD ( ).
∴EF∥ ( ).
∴∠FDG=∠EFD ( ).
18.(2022·吉林·长春外国语学校七年级期末)阅读下面的推理过程,将空白部分补充完整.
已知:如图,在△ABC中,FGCD,∠1 = ∠3.
求证:∠B + ∠BDE= 180°.
解:因为FGCD(已知),
所以∠1= .
又因为∠1 = ∠3 (已知),
所以∠2 = (等量代换).
所以BC ( ),
所以∠B + ∠BDE = 180°(___________________).
19.(2021·河南灵宝·七年级期中)如图,已知∠1+∠2=180°,∠3=∠B,求证:DE∥BC.
20.(2021·贵州碧江·七年级期末)如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
21.(2021·全国·七年级专题练习)如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D,
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
22.(2019·广西港南·七年级期末)已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
23.(2017·北京东城·七年级期中)已知:直线,点、分别在直线,上,点为平面内一点.
()如图,,,的数量关系是__________.
()利用()的结论解决问题:如图,已知,平分,平分,,求得度数.
()如图,点为上一点,,,交于点,直接写出,,之间的数量关系.(用含的式子表示)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A【解析】
①在同一平面内,不相交的两条直线叫做平行线,故原命题错误;
②过直线外一点,有且只有一条直线平行于已知直线,故原命题错误;
③两条平行直线被第三条直线所截,同位角相等,正确;
④同旁内角互补,两直线平行,故原命题错误.
故选:A
2.A【解】
解:∵AB⊥AC,∠1=52°,
∴∠B=90°﹣∠1
=90°﹣52°
=38°
∵a∥b,
∴∠2=∠B=38°.
故选:A.
3.A【详解】
解:如图,过三角板的直角顶点作直尺两边的平行线,
∵直尺的两边互相平行,
∴,
∴,
∴,
4.D【详解】
分析:由折叠可得:∠DGH=∠DGE=74°,再根据AD∥BC,即可得到∠GHC=180°﹣∠DGH=106°.
详解:∵∠AGE=32°,
∴∠DGE=148°,
由折叠可得:∠DGH=∠DGE=74°.
∵AD∥BC,
∴∠GHC=180°﹣∠DGH=106°.
故选D.
5.B【详解】
∵,
∴,
∵平分,
∴,
故选B.
6.B【详解】
由题意可得:∠EDF=45°,∠ABC=30°,
∵AB∥CF,
∴∠ABD=∠EDF=45°,
∴∠DBC=45°﹣30°=15°.
故选B.
7.C【详解】
分析:求出∠3即可解决问题;
详解:如图,
∵∠1+∠3=90°,∠1=35°,
∴∠3=55°,
∴∠2=∠3=55°,
故选C.
8.A【详解】
解:,
.
,
.
故选.
9.A【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFE=∠DEF=26°,
∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°,
故选A.
10.C【详解】
①如图1,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A+∠AEF=180°,∠C+∠CEF=180°,
所以∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°,则①错误;
②如图2,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A=∠AEF,∠C=∠CEF,
所以∠A+∠C=∠AEC+∠AEF=∠AEC,则②正确;
③如图3,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A+∠AEF=180°,∠1=∠CEF,所以∠A+∠AEC-∠1=∠A+∠AEC-∠CEF=∠A+∠AEF=180°,则③正确;
④如图4,过点P作PF∥AB,因为AB∥CD,所以AB∥PF∥CD,
所以∠A=∠APF,∠C=∠CPF,所以∠A=∠CPF+∠APC=∠C+∠APC,则④正确;
故选C.
11.50°【详解】
解:∵AB∥CD∥EF,
∴∠BCD=∠ABC=125°,∠CEF+∠ECD=180°,
∴∠ECD=180°-∠CEF=75°,
∴∠BCE=∠BCD-∠ECD=50°,
故答案为:50°.
12.32°【详解】
∵直线a∥b,AM⊥b,
∴AM⊥a;
∴∠2=180°-90°-∠1;
∵∠1=58°,
∴∠2=32°.
故答案是:32°.
13.54°【详解】
∵AB∥CD,
∴∠BEF=180° ∠1=180° 72°=108°
∠2=∠BEG,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°
∴∠2=∠BEG=54°.
故答案为54°.
14.①②③【详解】
①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣(180﹣a)°=a°,
∴∠BOF=∠BOD,
∴OF平分∠BOD所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=a°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=a°,所以④错误.
故答案为①②③.
15.(n+1)×180【详解】
解:如图,分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,
∵AB∥CD,
∴AB∥P1E∥P2F∥P3G.
由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°
∴(1)∠1+∠2=180°,
(2)∠1+∠P1+∠2=2×180,
(3)∠1+∠P1+∠P2+∠2=3×180°,
(4)∠1+∠P1+∠P2+∠P3+∠2=4×180°,
∴∠1+∠2+∠P1+…+∠Pn=(n+1)×180°.
故答案为:(n+1)×180.
16.【详解】
证明:∵AD∥BC(已知),
∴∠3=∠CAD(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠4=∠CAD(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质).
即∠BAF=∠CAD.
∴∠4=∠BAF.(等量代换).
∴AB∥CD(同位角相等,两直线平行).
17.【详解】
解:∵∠A=120°,∠FEC=120°(已知),
∴∠A=∠FEC(等量代换),
∴AB∥EF(同位角相等,两直线平行),
又∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
∴EF∥CD(平行于同一条直线的两直线互相平行),
∴∠FDG=∠EFD(两直线平行,内错角相等),
故答案为:∠FEC;等量代换;EF;同位角相等,两直线平行;内错角相等,两直线平行;CD;平行于同一条直线的两直线互相平行;两直线平行,内错角相等.
18.【详解】
解:因为FGCD(已知),
所以∠1=∠2.
又因为∠1 = ∠3 (已知),
所以∠2 =∠3(等量代换).
所以(内错角相等,两直线平行),
所以∠B + ∠BDE = 180°(两直线平行,同旁内角互补).
故答案为:∠2;∠3;DE;内错角相等,两直线平行;两直线平行,同旁内角互补.
19.【详解】
要证明DE∥BC.需证明∠3=∠EHC.而证明∠3=∠EHC可通过证明EF∥AB及已知条件∠3=∠B进行推理即可.
证明:∵∠1+∠2=180°,∠1=∠4,
∴∠2+∠4=180°.
∴EH∥AB.
∴∠B=∠EHC.
∵∠3=∠B,
∴∠3=∠EHC.
∴DE∥BC.
20.【详解】
证明:如图,设BC与AE、GF分别交于点M、N.
∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNB=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
21.【详解】
解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,
故答案为60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,即∠APB:∠ADB=2:1.
22.【详解】
(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)不成立
如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
23.
【解析】
整体分析:
(1)过作,结合平行公理和平行线的性质即可得到,,的数量关系;(2)直接利用(1)中的结论,结合角平分线的定义及平行线的性质即可;(3)利用平行线的性质和角平分线的定义及角的和差关系建立之间的数量关系.
解:()过作.
∵,
∴,
∴,,
∴
,
即:.
()∵平分,平分,
∴,,
∵,由()结论可知,
∴
,
∴
.
∵,
∴,
又∵
,
∴,
∴.
(),,之间的数量关系是.
∵,,
∴,,
∵,
∴,
∵
,
∴,
∵,
∴,
∴,
∴.
逆 袭 卷
