2021-2022学年九年级数学下册北师大版 3.9弧长及扇形面积 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年九年级数学下册北师大版 3.9弧长及扇形面积 同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 268.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 00:00:00 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学上册《3-9弧长及扇形面积》自主提升训练(附答案)
1.在半径为2的圆中,90°的圆心角所对的弧长为( )
A. B. C. D.π
2.如图,在半径2的圆形纸片中,剪一个圆心角为90°的扇形(图中阴影部分),则这个扇形的面积为( )
A.2π B.π C.π D.π
3.如图,在扇形BOC中,∠BOC=60°,点D为弧BC的中点,点E为半径OB上一动点,若OB=2,则阴影部分周长的最小值为( )
A.2+ B.+ C.+ D.2+
4.如图,点A、B、C、D都在边长为1的网格格点上,以A为圆心,AE为半径画弧,弧EF经过格点D,则扇形AEF的面积是( )
A. B. C.π D.
5.如图所示,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CO=2,则阴影部分的面积为( )
A.2π B.π C. D.
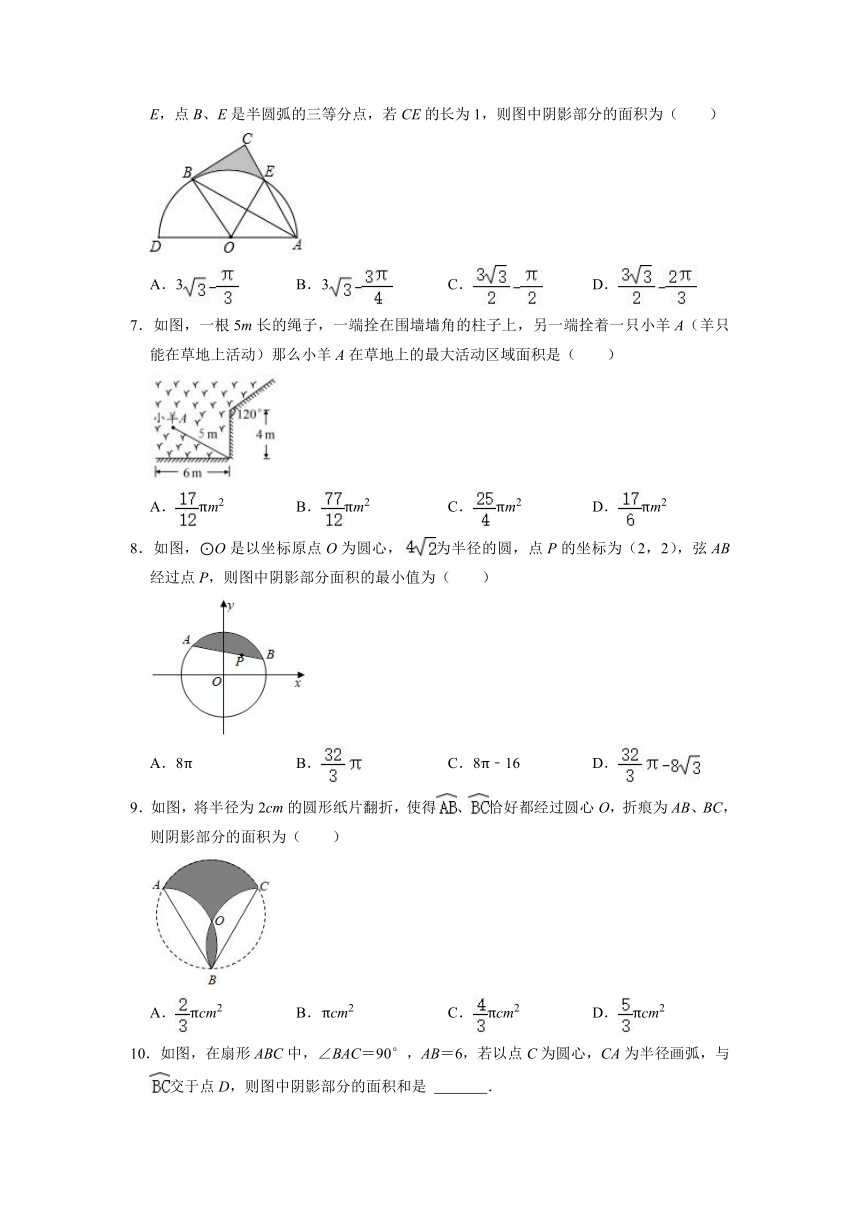
6.如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E,点B、E是半圆弧的三等分点,若CE的长为1,则图中阴影部分的面积为( )
A.3 B.3 C. D.
7.如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
A.πm2 B.πm2 C.πm2 D.πm2
8.如图,⊙O是以坐标原点O为圆心,为半径的圆,点P的坐标为(2,2),弦AB经过点P,则图中阴影部分面积的最小值为( )
A.8π B. C.8π﹣16 D.
9.如图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
10.如图,在扇形ABC中,∠BAC=90°,AB=6,若以点C为圆心,CA为半径画弧,与交于点D,则图中阴影部分的面积和是 .
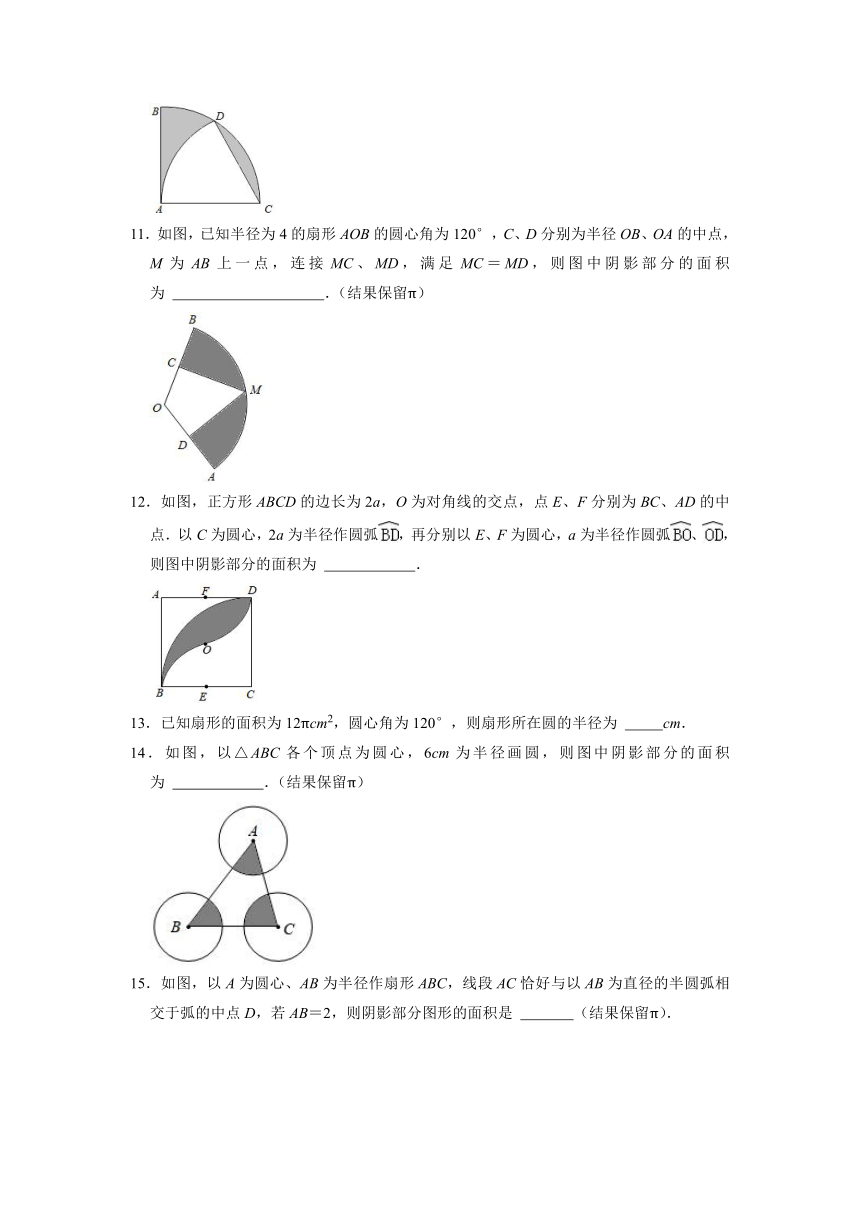
11.如图,已知半径为4的扇形AOB的圆心角为120°,C、D分别为半径OB、OA的中点,M为AB上一点,连接MC、MD,满足MC=MD,则图中阴影部分的面积为 .(结果保留π)
12.如图,正方形ABCD的边长为2a,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2a为半径作圆弧,再分别以E、F为圆心,a为半径作圆弧、,则图中阴影部分的面积为 .
13.已知扇形的面积为12πcm2,圆心角为120°,则扇形所在圆的半径为 cm.
14.如图,以△ABC各个顶点为圆心,6cm为半径画圆,则图中阴影部分的面积为 .(结果保留π)
15.如图,以A为圆心、AB为半径作扇形ABC,线段AC恰好与以AB为直径的半圆弧相交于弧的中点D,若AB=2,则阴影部分图形的面积是 (结果保留π).
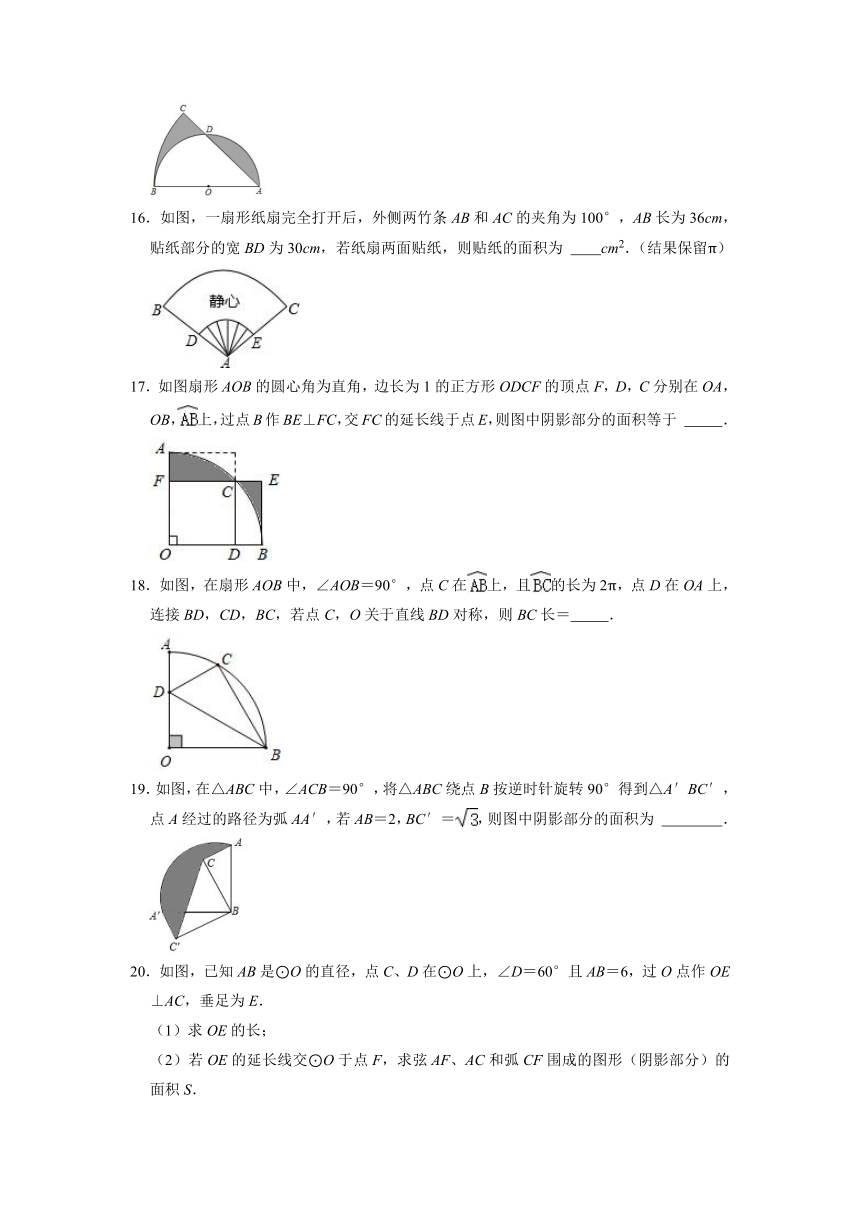
16.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为100°,AB长为36cm,贴纸部分的宽BD为30cm,若纸扇两面贴纸,则贴纸的面积为 cm2.(结果保留π)
17.如图扇形AOB的圆心角为直角,边长为1的正方形ODCF的顶点F,D,C分别在OA,OB,上,过点B作BE⊥FC,交FC的延长线于点E,则图中阴影部分的面积等于 .
18.如图,在扇形AOB中,∠AOB=90°,点C在上,且的长为2π,点D在OA上,连接BD,CD,BC,若点C,O关于直线BD对称,则BC长= .
19.如图,在△ABC中,∠ACB=90°,将△ABC绕点B按逆时针旋转90°得到△A′BC′,点A经过的路径为弧AA′,若AB=2,BC′=,则图中阴影部分的面积为 .
20.如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积S.
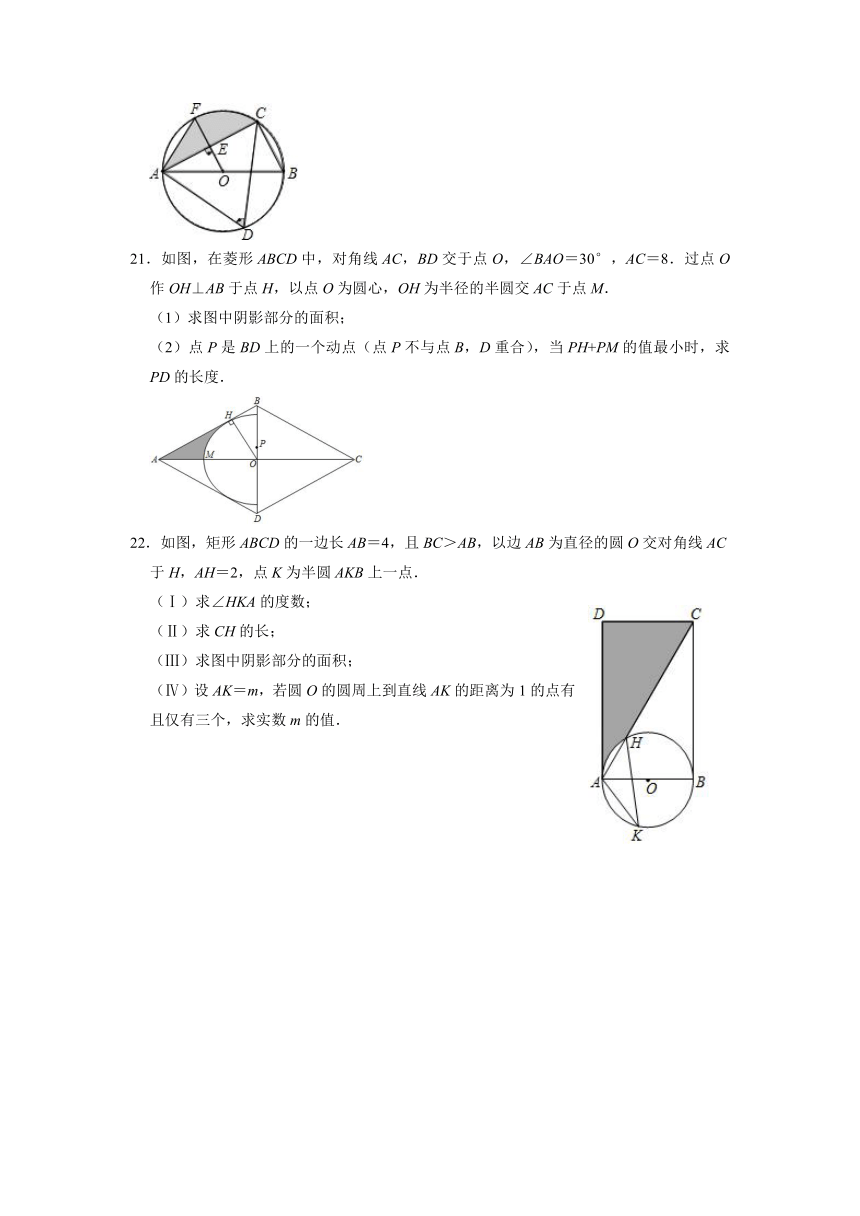
21.如图,在菱形ABCD中,对角线AC,BD交于点O,∠BAO=30°,AC=8.过点O作OH⊥AB于点H,以点O为圆心,OH为半径的半圆交AC于点M.
(1)求图中阴影部分的面积;
(2)点P是BD上的一个动点(点P不与点B,D重合),当PH+PM的值最小时,求PD的长度.
22.如图,矩形ABCD的一边长AB=4,且BC>AB,以边AB为直径的圆O交对角线AC于H,AH=2,点K为半圆AKB上一点.
(Ⅰ)求∠HKA的度数;
(Ⅱ)求CH的长;
(Ⅲ)求图中阴影部分的面积;
(Ⅳ)设AK=m,若圆O的圆周上到直线AK的距离为1的点有且仅有三个,求实数m的值.
参考答案
1.解:根据弧长的公式l=,得l==π,
故选:D.
2.解:连接BC,
由∠BAC=90°得BC为⊙O的直径,
∴BC=4,
在Rt△ABC中,由勾股定理可得:AB=AC=2,
∴S扇形ABC==2π,故选:A.
3.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===2,
的长l==,
∴阴影部分周长的最小值为2+.故选:D.
4.解:由题意,扇形的半径AD==,∠EAF=45°,
∴扇形AEF的面积==.
故选:A.
5.解:如图,由圆的对称性知:S阴影=S扇形BOC==,
故选:D.
6.解:连接BD,BE,
∵B,E是半圆弧的三等分点,
∴∠EOA=∠EOB=∠BOD=60°,
∴∠BAC=∠EBA=30°,
∴BE∥AD,∠BEC=60°,
∵CE=1,
∴BE=2,
∴AD=2BE=4,
∴AB=ADcos30°=2,
∴BC=AB=,
∴AC=AB=3,
∴S△ABC=×BC×AC=××3=,
∵△BOE和△ABE同底等高,
∴△BOE和△ABE面积相等,
∴图中阴影部分的面积为:S△ABC﹣S扇形BOE=﹣=﹣π.
故选:D.
7.解:大扇形的圆心角是90度,半径是5,
所以面积==π(m2);
小扇形的圆心角是180°﹣120°=60°,半径是1m,
则面积==(m2),
则小羊A在草地上的最大活动区域面积=π+=π(m2).
故选:B.
8.解:由题意当OP⊥A'B'时,阴影部分的面积最小,
∵P(2,2),
∴OP=2,
∵OA'=OB'=4,
∴cos∠A'OP=cos∠B'OP=,
∴∠A'OP=∠B'OP=60°,
∴∠A'OB'=120°,A′P=4×=2,
∴A′B′=4
∴S阴=S扇形OA'B'﹣S△A'OB'=﹣=π﹣8,
故选:D.
9.解:作OD⊥AB于点D,连接AO,BO,CO,如图所示:
∵OD=AO
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形BOC=×⊙O面积=×π×22=π(cm2);
故选:C.
10.解:连接AD,
∵以点C为圆心,CA为半径画弧,与交于点D,AB=6,
∴AD=AC=CD=6,
∴△ADC是等边三角形,
∴∠DCA=∠DAC=60°,
∵∠BAC=90°,
∴∠BAD=∠BAC﹣∠DAC=90°﹣60°=30°,
∴阴影部分的面积=S扇形BAD==3π,
故答案为:3π.
11.解:连接OM、MB、MA,如右图所示,
∵C、D分别为半径OB、OA的中点,
∴OC=OD,
在△OCM和△ODM中,
,
∴△OCM≌△ODM(SSS),
∴∠COM=∠DOM,
∵∠COD=120°,
∴∠COM=∠DOM=60°,
∵OB=OM=OA=4,
∴△OMB和△OMA都是等边三角形,
∴MC=OM sin60°=4×=2,
∴S阴影=S扇形OBA﹣S△OCM﹣S△ODM=﹣=,
故答案为:.
12.解:连接BD,EF,如图,
∵正方形ABCD的边长为2a,O为对角线的交点,
由题意可得:EF,BD经过点O,且EF⊥AD,EF⊥CB.
∵点E,F分别为BC,AD的中点,
∴FD=FO=EO=EB=a,
∴=,OB=OD.
∴弓形OB=弓形OD.
∴阴影部分的面积等于弓形BD的面积.
∴S阴影=S扇形CBD﹣S△CBD=﹣×2a×2a=πa2﹣2a2.
故答案为:πa2﹣2a2.
13.解:设该扇形的半径是rcm,则
12π=,
解得r=6.
故答案为:6.
14.解:由图知,阴影部分的3个扇形的圆心角组成了三角形的3个内角,
∵三角形的内角和为180°,
又∵6cm为半径,
∴=18π(cm2),
故答案为:18πcm2.
15.解:连接DO,
∵线段AC交以AB为直径的半圆弧的中点D,AB=2,
∴∠DAO=45°,∠DOA=90°,DO=AO=1,
∴阴影部分的面积是:(﹣﹣×1×1)+(=×1×1)=π﹣1,
故答案为:π﹣1.
16.解:∵AB长为36cm,贴纸部分的宽BD为30cm,
∴AD=6cm,
∴贴纸的面积为S=2×(S扇形ABC﹣S扇形ADE)=2×(﹣)=350π(cm2),
故答案为:350π.
17.解:连接OC,
∵正方形的边长为1,即OD=CD=1,
∴OC==,
∴BD=OB﹣OD=﹣1,
∵OA=OB,OF=OD,
∴AF=BD,
∵CF=CD,
∴阴影部分的面积=长方形CDBE的面积=﹣1,
故答案为:﹣1.
18.解:连接BC,OC,OC交BD于W,
∵点C,O关于直线BD对称,
∴∠DWO=90°,OW=CW,BC=OB,
∵OC=OB,
∴OC=BC=OB,
即△OCB是等边三角形,
∴∠COB=60°,
∵的长为2π,
∴=2π,
解得:OB=6,
∴BC=OB=6,
故答案为:6.
19.解:∵将△ABC绕点B按逆时针旋转90°得到△A′BC′,点A经过的路径为弧AA′,BC′=,
∵BC=BC′=,AC=A′C′,
由勾股定理得:AC===1,即A′C′=1,
∵阴影部分的面积=扇形ABA′的面积+△BA′C′的面积﹣△ACB的面积﹣△CBC′的面积,
∴图中阴影部分的面积S=+﹣﹣
=π﹣,
故答案为:π﹣.
20.解:(1)∵∠D=60°,
∴∠B=60°(圆周角定理),
又∵AB=6,
∴BC=3,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OE⊥AC,
∴OE∥BC,
又∵点O是AB中点,
∴OE是△ABC的中位线,
∴OE=BC=;
(2)连接OC,
则易得△COE≌△AFE,
故阴影部分的面积=扇形FOC的面积,
S扇形FOC==π.
即可得阴影部分的面积为π.
21.解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=4,
∵OH⊥AB,
∴∠AHO=90°,
∵∠OAH=30°,
∴∠AOH=60°,OH=OA=2,AH=OH=2,
∴S阴=S△AOH﹣S扇形OMH=×2×2﹣=2﹣π.
(2)作点M关于BD的对称点M′,连接HM′交BD于P,连接PM,连接PM,此时PH+PM的值最小.
∵OH=OM′,
∴∠OHM′=∠OM′H,
∵∠AOH=∠OHM′+∠OM′H=60°,
设OP=m,则PM=2m,
∵PM2=OM2+OP2,
∴4m2=m2+22,
∴m=,
∴PD=OD+OP=+=2.
22.解:(Ⅰ)连接BH,
∵AB为⊙O的直径,
∴∠AHB=90°,
∵AB=4,AH=2,
∴sin∠ABH===,
∴∠ABH=30°,
∴∠HKA=∠ABH=30°;
(Ⅱ)∵∠AHB=90°,∠ABH=30°,
∴∠BAH=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=2AB=8,
∴CH=AC﹣AH=6;
(Ⅲ)连接OH,则△AOH是等边三角形,
∴AO=AH=2,∠AOH=60°,
过H作HE⊥AO于E,则HE=,
∵AC=8,CD=AB=4,
∴AD=4,
∴图中阴影部分的面积=×44﹣(﹣×2×)=9﹣π;
(Ⅳ)过O作平行于AK的直线交⊙O于MN,过O作OP⊥AK于Q交⊙O于P,
∵⊙O的半径=2,则PQ=OQ=1,
∵OA=2,
∴AQ=,
∴AK=2AQ=2,∴m=2.
1.在半径为2的圆中,90°的圆心角所对的弧长为( )
A. B. C. D.π
2.如图,在半径2的圆形纸片中,剪一个圆心角为90°的扇形(图中阴影部分),则这个扇形的面积为( )
A.2π B.π C.π D.π
3.如图,在扇形BOC中,∠BOC=60°,点D为弧BC的中点,点E为半径OB上一动点,若OB=2,则阴影部分周长的最小值为( )
A.2+ B.+ C.+ D.2+
4.如图,点A、B、C、D都在边长为1的网格格点上,以A为圆心,AE为半径画弧,弧EF经过格点D,则扇形AEF的面积是( )
A. B. C.π D.
5.如图所示,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CO=2,则阴影部分的面积为( )
A.2π B.π C. D.
6.如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E,点B、E是半圆弧的三等分点,若CE的长为1,则图中阴影部分的面积为( )
A.3 B.3 C. D.
7.如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
A.πm2 B.πm2 C.πm2 D.πm2
8.如图,⊙O是以坐标原点O为圆心,为半径的圆,点P的坐标为(2,2),弦AB经过点P,则图中阴影部分面积的最小值为( )
A.8π B. C.8π﹣16 D.
9.如图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
10.如图,在扇形ABC中,∠BAC=90°,AB=6,若以点C为圆心,CA为半径画弧,与交于点D,则图中阴影部分的面积和是 .
11.如图,已知半径为4的扇形AOB的圆心角为120°,C、D分别为半径OB、OA的中点,M为AB上一点,连接MC、MD,满足MC=MD,则图中阴影部分的面积为 .(结果保留π)
12.如图,正方形ABCD的边长为2a,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2a为半径作圆弧,再分别以E、F为圆心,a为半径作圆弧、,则图中阴影部分的面积为 .
13.已知扇形的面积为12πcm2,圆心角为120°,则扇形所在圆的半径为 cm.
14.如图,以△ABC各个顶点为圆心,6cm为半径画圆,则图中阴影部分的面积为 .(结果保留π)
15.如图,以A为圆心、AB为半径作扇形ABC,线段AC恰好与以AB为直径的半圆弧相交于弧的中点D,若AB=2,则阴影部分图形的面积是 (结果保留π).
16.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为100°,AB长为36cm,贴纸部分的宽BD为30cm,若纸扇两面贴纸,则贴纸的面积为 cm2.(结果保留π)
17.如图扇形AOB的圆心角为直角,边长为1的正方形ODCF的顶点F,D,C分别在OA,OB,上,过点B作BE⊥FC,交FC的延长线于点E,则图中阴影部分的面积等于 .
18.如图,在扇形AOB中,∠AOB=90°,点C在上,且的长为2π,点D在OA上,连接BD,CD,BC,若点C,O关于直线BD对称,则BC长= .
19.如图,在△ABC中,∠ACB=90°,将△ABC绕点B按逆时针旋转90°得到△A′BC′,点A经过的路径为弧AA′,若AB=2,BC′=,则图中阴影部分的面积为 .
20.如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积S.
21.如图,在菱形ABCD中,对角线AC,BD交于点O,∠BAO=30°,AC=8.过点O作OH⊥AB于点H,以点O为圆心,OH为半径的半圆交AC于点M.
(1)求图中阴影部分的面积;
(2)点P是BD上的一个动点(点P不与点B,D重合),当PH+PM的值最小时,求PD的长度.
22.如图,矩形ABCD的一边长AB=4,且BC>AB,以边AB为直径的圆O交对角线AC于H,AH=2,点K为半圆AKB上一点.
(Ⅰ)求∠HKA的度数;
(Ⅱ)求CH的长;
(Ⅲ)求图中阴影部分的面积;
(Ⅳ)设AK=m,若圆O的圆周上到直线AK的距离为1的点有且仅有三个,求实数m的值.
参考答案
1.解:根据弧长的公式l=,得l==π,
故选:D.
2.解:连接BC,
由∠BAC=90°得BC为⊙O的直径,
∴BC=4,
在Rt△ABC中,由勾股定理可得:AB=AC=2,
∴S扇形ABC==2π,故选:A.
3.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===2,
的长l==,
∴阴影部分周长的最小值为2+.故选:D.
4.解:由题意,扇形的半径AD==,∠EAF=45°,
∴扇形AEF的面积==.
故选:A.
5.解:如图,由圆的对称性知:S阴影=S扇形BOC==,
故选:D.
6.解:连接BD,BE,
∵B,E是半圆弧的三等分点,
∴∠EOA=∠EOB=∠BOD=60°,
∴∠BAC=∠EBA=30°,
∴BE∥AD,∠BEC=60°,
∵CE=1,
∴BE=2,
∴AD=2BE=4,
∴AB=ADcos30°=2,
∴BC=AB=,
∴AC=AB=3,
∴S△ABC=×BC×AC=××3=,
∵△BOE和△ABE同底等高,
∴△BOE和△ABE面积相等,
∴图中阴影部分的面积为:S△ABC﹣S扇形BOE=﹣=﹣π.
故选:D.
7.解:大扇形的圆心角是90度,半径是5,
所以面积==π(m2);
小扇形的圆心角是180°﹣120°=60°,半径是1m,
则面积==(m2),
则小羊A在草地上的最大活动区域面积=π+=π(m2).
故选:B.
8.解:由题意当OP⊥A'B'时,阴影部分的面积最小,
∵P(2,2),
∴OP=2,
∵OA'=OB'=4,
∴cos∠A'OP=cos∠B'OP=,
∴∠A'OP=∠B'OP=60°,
∴∠A'OB'=120°,A′P=4×=2,
∴A′B′=4
∴S阴=S扇形OA'B'﹣S△A'OB'=﹣=π﹣8,
故选:D.
9.解:作OD⊥AB于点D,连接AO,BO,CO,如图所示:
∵OD=AO
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形BOC=×⊙O面积=×π×22=π(cm2);
故选:C.
10.解:连接AD,
∵以点C为圆心,CA为半径画弧,与交于点D,AB=6,
∴AD=AC=CD=6,
∴△ADC是等边三角形,
∴∠DCA=∠DAC=60°,
∵∠BAC=90°,
∴∠BAD=∠BAC﹣∠DAC=90°﹣60°=30°,
∴阴影部分的面积=S扇形BAD==3π,
故答案为:3π.
11.解:连接OM、MB、MA,如右图所示,
∵C、D分别为半径OB、OA的中点,
∴OC=OD,
在△OCM和△ODM中,
,
∴△OCM≌△ODM(SSS),
∴∠COM=∠DOM,
∵∠COD=120°,
∴∠COM=∠DOM=60°,
∵OB=OM=OA=4,
∴△OMB和△OMA都是等边三角形,
∴MC=OM sin60°=4×=2,
∴S阴影=S扇形OBA﹣S△OCM﹣S△ODM=﹣=,
故答案为:.
12.解:连接BD,EF,如图,
∵正方形ABCD的边长为2a,O为对角线的交点,
由题意可得:EF,BD经过点O,且EF⊥AD,EF⊥CB.
∵点E,F分别为BC,AD的中点,
∴FD=FO=EO=EB=a,
∴=,OB=OD.
∴弓形OB=弓形OD.
∴阴影部分的面积等于弓形BD的面积.
∴S阴影=S扇形CBD﹣S△CBD=﹣×2a×2a=πa2﹣2a2.
故答案为:πa2﹣2a2.
13.解:设该扇形的半径是rcm,则
12π=,
解得r=6.
故答案为:6.
14.解:由图知,阴影部分的3个扇形的圆心角组成了三角形的3个内角,
∵三角形的内角和为180°,
又∵6cm为半径,
∴=18π(cm2),
故答案为:18πcm2.
15.解:连接DO,
∵线段AC交以AB为直径的半圆弧的中点D,AB=2,
∴∠DAO=45°,∠DOA=90°,DO=AO=1,
∴阴影部分的面积是:(﹣﹣×1×1)+(=×1×1)=π﹣1,
故答案为:π﹣1.
16.解:∵AB长为36cm,贴纸部分的宽BD为30cm,
∴AD=6cm,
∴贴纸的面积为S=2×(S扇形ABC﹣S扇形ADE)=2×(﹣)=350π(cm2),
故答案为:350π.
17.解:连接OC,
∵正方形的边长为1,即OD=CD=1,
∴OC==,
∴BD=OB﹣OD=﹣1,
∵OA=OB,OF=OD,
∴AF=BD,
∵CF=CD,
∴阴影部分的面积=长方形CDBE的面积=﹣1,
故答案为:﹣1.
18.解:连接BC,OC,OC交BD于W,
∵点C,O关于直线BD对称,
∴∠DWO=90°,OW=CW,BC=OB,
∵OC=OB,
∴OC=BC=OB,
即△OCB是等边三角形,
∴∠COB=60°,
∵的长为2π,
∴=2π,
解得:OB=6,
∴BC=OB=6,
故答案为:6.
19.解:∵将△ABC绕点B按逆时针旋转90°得到△A′BC′,点A经过的路径为弧AA′,BC′=,
∵BC=BC′=,AC=A′C′,
由勾股定理得:AC===1,即A′C′=1,
∵阴影部分的面积=扇形ABA′的面积+△BA′C′的面积﹣△ACB的面积﹣△CBC′的面积,
∴图中阴影部分的面积S=+﹣﹣
=π﹣,
故答案为:π﹣.
20.解:(1)∵∠D=60°,
∴∠B=60°(圆周角定理),
又∵AB=6,
∴BC=3,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OE⊥AC,
∴OE∥BC,
又∵点O是AB中点,
∴OE是△ABC的中位线,
∴OE=BC=;
(2)连接OC,
则易得△COE≌△AFE,
故阴影部分的面积=扇形FOC的面积,
S扇形FOC==π.
即可得阴影部分的面积为π.
21.解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=4,
∵OH⊥AB,
∴∠AHO=90°,
∵∠OAH=30°,
∴∠AOH=60°,OH=OA=2,AH=OH=2,
∴S阴=S△AOH﹣S扇形OMH=×2×2﹣=2﹣π.
(2)作点M关于BD的对称点M′,连接HM′交BD于P,连接PM,连接PM,此时PH+PM的值最小.
∵OH=OM′,
∴∠OHM′=∠OM′H,
∵∠AOH=∠OHM′+∠OM′H=60°,
设OP=m,则PM=2m,
∵PM2=OM2+OP2,
∴4m2=m2+22,
∴m=,
∴PD=OD+OP=+=2.
22.解:(Ⅰ)连接BH,
∵AB为⊙O的直径,
∴∠AHB=90°,
∵AB=4,AH=2,
∴sin∠ABH===,
∴∠ABH=30°,
∴∠HKA=∠ABH=30°;
(Ⅱ)∵∠AHB=90°,∠ABH=30°,
∴∠BAH=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=2AB=8,
∴CH=AC﹣AH=6;
(Ⅲ)连接OH,则△AOH是等边三角形,
∴AO=AH=2,∠AOH=60°,
过H作HE⊥AO于E,则HE=,
∵AC=8,CD=AB=4,
∴AD=4,
∴图中阴影部分的面积=×44﹣(﹣×2×)=9﹣π;
(Ⅳ)过O作平行于AK的直线交⊙O于MN,过O作OP⊥AK于Q交⊙O于P,
∵⊙O的半径=2,则PQ=OQ=1,
∵OA=2,
∴AQ=,
∴AK=2AQ=2,∴m=2.
