山东省聊城市莘县2021-2022学年九年级上学期期中数学试题(word版含答案)
文档属性
| 名称 | 山东省聊城市莘县2021-2022学年九年级上学期期中数学试题(word版含答案) | 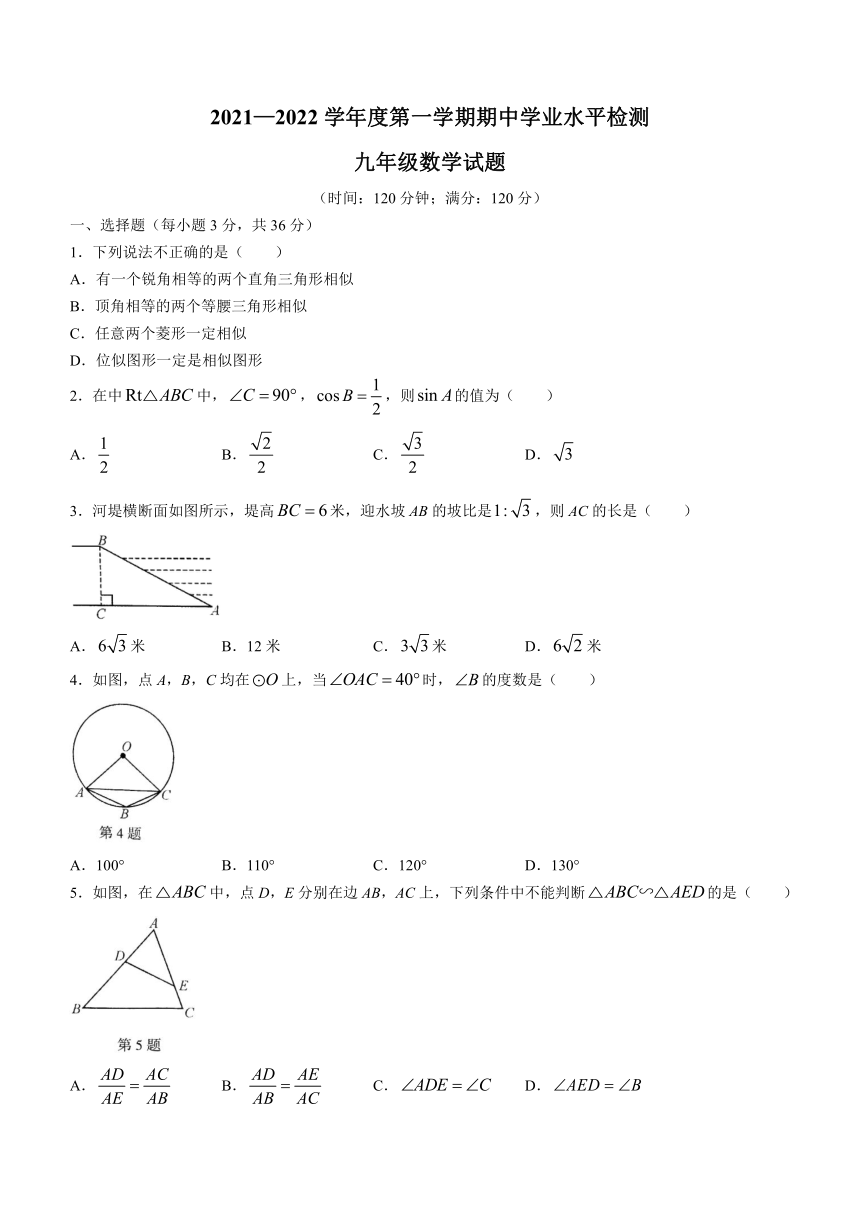 | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 15:57:09 | ||
图片预览



文档简介
2021—2022学年度第一学期期中学业水平检测
九年级数学试题
(时间:120分钟;满分:120分)
一、选择题(每小题3分,共36分)
1.下列说法不正确的是( )
A.有一个锐角相等的两个直角三角形相似
B.顶角相等的两个等腰三角形相似
C.任意两个菱形一定相似
D.位似图形一定是相似图形
2.在中中,,,则的值为( )
A. B. C. D.
3.河堤横断面如图所示,堤高米,迎水坡AB的坡比是,则AC的长是( )
A.米 B.12米 C.米 D.米
4.如图,点A,B,C均在上,当时,的度数是( )
A.100° B.110° C.120° D.130°
5.如图,在中,点D,E分别在边AB,AC上,下列条件中不能判断的是( )
A. B. C. D.
6.如图,的顶点都在正方形网格的格点上,则的值为( )
A. B. C. D.
7.已知半径为5的圆,直线l上一点到圆心的距离是5,则直线和圆的位置关系为( )
A.相切 B.相离 C.相切或相交 D.相切或相离
8.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.海里 C.海里 D.海里
9.如图,AB是的直径,点C,D,E在上,若,则的度数为( )
A.100° B.110° C.115° D.120°
10.如图,的直径,AB是的弦,,垂足为M,,则AB的长为( )
A.8 B.12 C.16 D.
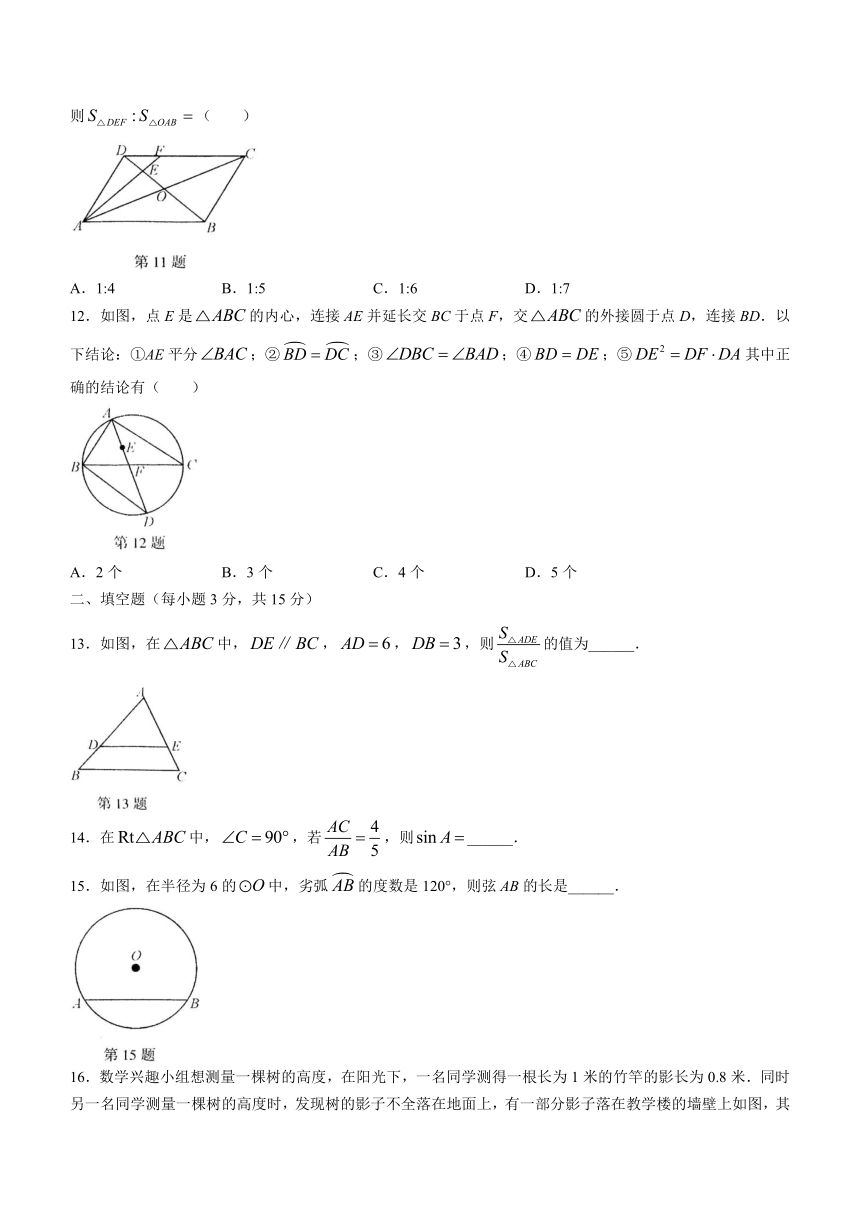
11.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则( )
A.1:4 B.1:5 C.1:6 D.1:7
12.如图,点E是的内心,连接AE并延长交BC于点F,交的外接圆于点D,连接BD.以下结论:①AE平分;②;③;④;⑤其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共15分)
13.如图,在中,,,,则的值为______.
14.在中,,若,则______.
15.如图,在半径为6的中,劣弧的度数是120°,则弦AB的长是______.
16.数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上如图,其影长为1.2米,落在地面上的影长2.4米,则树高为______米.
17.如图,在中,,,,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为______.
三、解答题:(69分)
18.化简(每小题4分,共8分)
(1)
(2).
19.(7分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,的顶点都在格点上,建立如图所示的平面直角坐标系.
(1)将向左平移2个单位再向上平移1个单位,平移后点A的对应点的坐标为______,内坐标为的一点M平移后对应点的坐标为______.
(2)以原点为位似中心,将缩小,使变换后得到的与对应边的比为1:2,请在网格中的第三象限画出.
20.(8分)如图,在中,,AD为BC边上的中线,于点E.
(1)求证:.
(2)若,,求线段DE的长.
21.(8分)禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度结果保留根号.
22.(8分)如图,在正方形ABCD中,E、F分别是边AD、CD上的点,,,连接EF并延长交BC的延长线于点G.
(1)求证:;
(2)若正方形的边长为8,求BG的长.
23.(8分)如图,AB是半圆的直径,C,D是半圆上的两点,且的度数为40°,,求的度数.
24.(10分)如图,为加快5G网络建设,某移动通信公司在一个坡度为2:1的山腰上建了一座垂直于水平面的5G信号通信塔AB,在距山脚C处水平距离39米的点D处测得通信塔底B处的仰角是25°,通信塔顶A处的仰角是42°.请求出通信塔AB的大约高度(结果保留整数,参考数据:,,,).
25.(12分)如图,AB为的直径,C、D为上的两点,,过点C做直线,交AD的延长线于点E,连接BC.
(1)求证:EF是的切线;
(2)若,,求劣弧的长l.
2021—2022学年度第一学期期中学业水平检测
九年级数学参考答案
一、选择题(每小题3分,共36分)
1.C 2.A 3.A 4.D 5.B 6.A 7.C 8.B 9.B 10.C 11.C 12.D
二、填空题(每小题3分,共15分)
13. 14. 15. 16.4.2 17.
三、解答题:(69分)
18.(每小题4分)
解:(1)原式;
(2)原式.
19.解:(1)(3分)
(2)(4分)即为所求.
20.(8分)
解:(1)∵,,∴,,
∵,∴,∴;
(2)∵,,∴,
在中,,
∵,∴.
21.(8分)
解:过点C作,再足为点D,设海里,则海里,
∵,∴,∵,∴,
在中,则,
则,解得:,即.
在中,,解得:,
则(海里/时),
则该可疑船只的航行速度约为海里/时.
22.(8分)
(1)证明:∵ABCD为正方形,
∴,,∵,∴,
∵,∴,∴,又,∴;
(2)解:∵ABCD为正方形,∴,∴,
又∵,正方形的边长为8,∴,,∴.
23.(8分)
解:∵AB是半圆的直径,∴,
∵的度数为40°,∴,∴,
∵四边形ABCD是的内接四边形,∴.
∵,∴,∴.
24.(10分)
解:延长AB交DC延长线于点E,则,
由题意知,,,
∵BC的坡度为2:1,∴设,则,,
在中,,
即,解得:,∴,,
在中,,
则,答:通信塔AB的大约高度为21米.
25.(12分)
(1)证明:连接OC,
∵,∴,∴,∴,
∵,∴,∴EF是的切线;
(2)连接OD,DC,
∵,,∴,∴,
∴,∴,∴,
∵,∴是等边三角形,
∴,,∴.
九年级数学试题
(时间:120分钟;满分:120分)
一、选择题(每小题3分,共36分)
1.下列说法不正确的是( )
A.有一个锐角相等的两个直角三角形相似
B.顶角相等的两个等腰三角形相似
C.任意两个菱形一定相似
D.位似图形一定是相似图形
2.在中中,,,则的值为( )
A. B. C. D.
3.河堤横断面如图所示,堤高米,迎水坡AB的坡比是,则AC的长是( )
A.米 B.12米 C.米 D.米
4.如图,点A,B,C均在上,当时,的度数是( )
A.100° B.110° C.120° D.130°
5.如图,在中,点D,E分别在边AB,AC上,下列条件中不能判断的是( )
A. B. C. D.
6.如图,的顶点都在正方形网格的格点上,则的值为( )
A. B. C. D.
7.已知半径为5的圆,直线l上一点到圆心的距离是5,则直线和圆的位置关系为( )
A.相切 B.相离 C.相切或相交 D.相切或相离
8.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.海里 C.海里 D.海里
9.如图,AB是的直径,点C,D,E在上,若,则的度数为( )
A.100° B.110° C.115° D.120°
10.如图,的直径,AB是的弦,,垂足为M,,则AB的长为( )
A.8 B.12 C.16 D.
11.如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则( )
A.1:4 B.1:5 C.1:6 D.1:7
12.如图,点E是的内心,连接AE并延长交BC于点F,交的外接圆于点D,连接BD.以下结论:①AE平分;②;③;④;⑤其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共15分)
13.如图,在中,,,,则的值为______.
14.在中,,若,则______.
15.如图,在半径为6的中,劣弧的度数是120°,则弦AB的长是______.
16.数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上如图,其影长为1.2米,落在地面上的影长2.4米,则树高为______米.
17.如图,在中,,,,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为______.
三、解答题:(69分)
18.化简(每小题4分,共8分)
(1)
(2).
19.(7分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,的顶点都在格点上,建立如图所示的平面直角坐标系.
(1)将向左平移2个单位再向上平移1个单位,平移后点A的对应点的坐标为______,内坐标为的一点M平移后对应点的坐标为______.
(2)以原点为位似中心,将缩小,使变换后得到的与对应边的比为1:2,请在网格中的第三象限画出.
20.(8分)如图,在中,,AD为BC边上的中线,于点E.
(1)求证:.
(2)若,,求线段DE的长.
21.(8分)禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度结果保留根号.
22.(8分)如图,在正方形ABCD中,E、F分别是边AD、CD上的点,,,连接EF并延长交BC的延长线于点G.
(1)求证:;
(2)若正方形的边长为8,求BG的长.
23.(8分)如图,AB是半圆的直径,C,D是半圆上的两点,且的度数为40°,,求的度数.
24.(10分)如图,为加快5G网络建设,某移动通信公司在一个坡度为2:1的山腰上建了一座垂直于水平面的5G信号通信塔AB,在距山脚C处水平距离39米的点D处测得通信塔底B处的仰角是25°,通信塔顶A处的仰角是42°.请求出通信塔AB的大约高度(结果保留整数,参考数据:,,,).
25.(12分)如图,AB为的直径,C、D为上的两点,,过点C做直线,交AD的延长线于点E,连接BC.
(1)求证:EF是的切线;
(2)若,,求劣弧的长l.
2021—2022学年度第一学期期中学业水平检测
九年级数学参考答案
一、选择题(每小题3分,共36分)
1.C 2.A 3.A 4.D 5.B 6.A 7.C 8.B 9.B 10.C 11.C 12.D
二、填空题(每小题3分,共15分)
13. 14. 15. 16.4.2 17.
三、解答题:(69分)
18.(每小题4分)
解:(1)原式;
(2)原式.
19.解:(1)(3分)
(2)(4分)即为所求.
20.(8分)
解:(1)∵,,∴,,
∵,∴,∴;
(2)∵,,∴,
在中,,
∵,∴.
21.(8分)
解:过点C作,再足为点D,设海里,则海里,
∵,∴,∵,∴,
在中,则,
则,解得:,即.
在中,,解得:,
则(海里/时),
则该可疑船只的航行速度约为海里/时.
22.(8分)
(1)证明:∵ABCD为正方形,
∴,,∵,∴,
∵,∴,∴,又,∴;
(2)解:∵ABCD为正方形,∴,∴,
又∵,正方形的边长为8,∴,,∴.
23.(8分)
解:∵AB是半圆的直径,∴,
∵的度数为40°,∴,∴,
∵四边形ABCD是的内接四边形,∴.
∵,∴,∴.
24.(10分)
解:延长AB交DC延长线于点E,则,
由题意知,,,
∵BC的坡度为2:1,∴设,则,,
在中,,
即,解得:,∴,,
在中,,
则,答:通信塔AB的大约高度为21米.
25.(12分)
(1)证明:连接OC,
∵,∴,∴,∴,
∵,∴,∴EF是的切线;
(2)连接OD,DC,
∵,,∴,∴,
∴,∴,∴,
∵,∴是等边三角形,
∴,,∴.
同课章节目录
