2021-2022学年九年级数学下册人教版第二十七章 相似 单元测试训练卷(word版含答案)
文档属性
| 名称 | 2021-2022学年九年级数学下册人教版第二十七章 相似 单元测试训练卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 122.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 07:52:17 | ||
图片预览



文档简介
人教版九年级数学下册
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
2. 已知=,那么的值为( )
A. B. C. D.
3. 在比例尺为1:150 000的某城市地图上,若量得A、B两所学校的距离是4.2厘米,则A、B两所学校的实际距离是( )
A.630米 B.6 300米 C.8 400米 D.4 200米
4. 如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判定△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C
C.= D.=
5. 如图,在6×6的正方形网格中,连接两格点A,B,线段AB与网格线的交点为M,N,则AM∶MN∶NB为( )
A.3∶5∶4 B.1∶3∶2
C.1∶4∶2 D.3∶6∶5
6. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )
A.1.5 里 B.1.2 里
C.1.05 里 D.1.02 里
7. 如图,已知△ABC和△ADE均为等边三角形,点D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A.1 B.2 C.3 D.4
8. 如图,已知△OAB与△OA′B′是相似比为1∶2的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
A.(-x,-y) B.(-2x,-2y)
C.(-2x,2y) D.(2x,-2y)
9.如图,在边长为1 的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A.(0,0) B.(0,1) C.(-3,2) D.(3,-2)
10. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,4*6=24)
11. 已知=,则=__ __,=__ __.
12. 如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是__ __米.
13. 在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是__ __.
14. 如图,在△ABC中,E,F分别是边AB,AC上的点,且满足==,则△AEF与△ABC的面积比是________.
15.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB,AD的中点,GE⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=__ __里.
16.如图, ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①EO⊥AC;②S△AOD=4S△OCF;③AC∶BD=∶7;④FB2=OF·DF.其中正确的结论有__________(填写所有正确结论的序号).
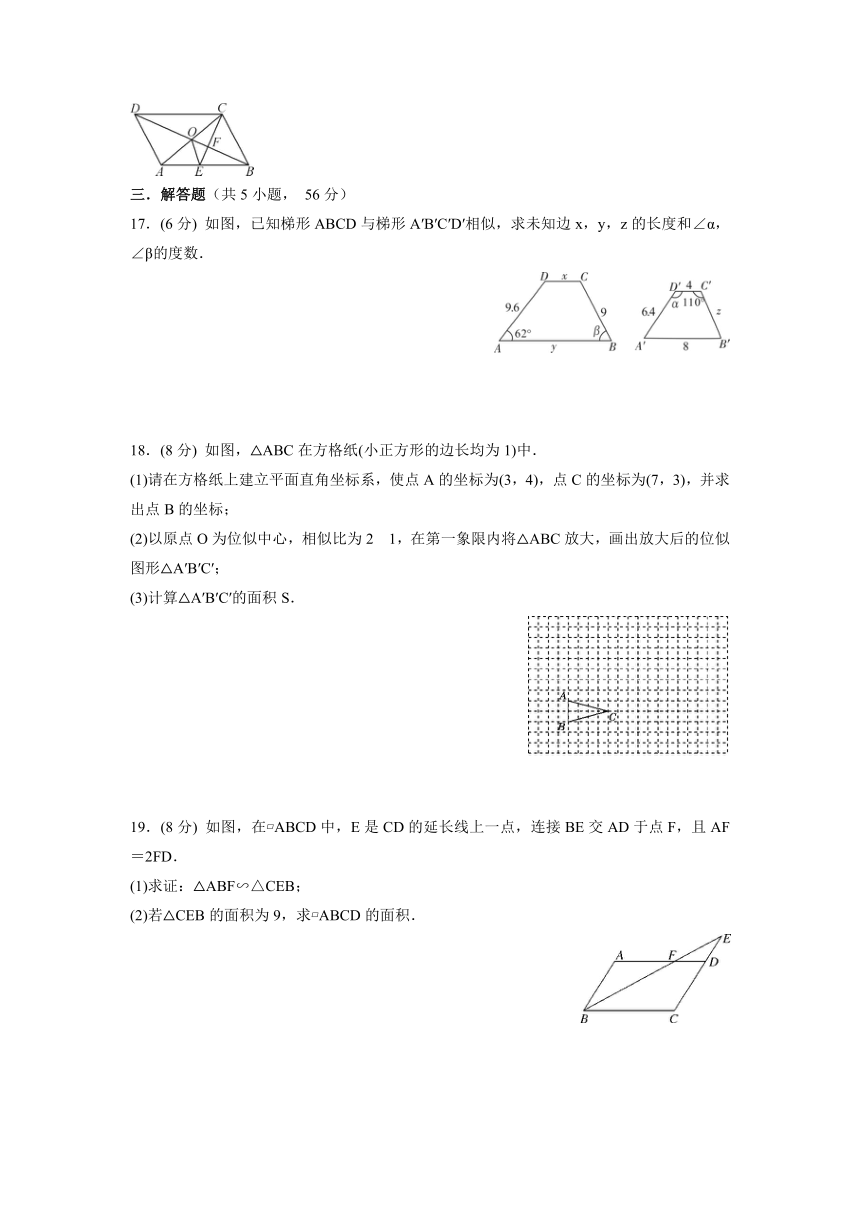
三.解答题(共5小题, 56分)
17.(6分) 如图,已知梯形ABCD与梯形A′B′C′D′相似,求未知边x,y,z的长度和∠α,∠β的度数.
18.(8分) 如图,△ABC在方格纸(小正方形的边长均为1)中.
(1)请在方格纸上建立平面直角坐标系,使点A的坐标为(3,4),点C的坐标为(7,3),并求出点B的坐标;
(2)以原点O为位似中心,相似比为2?1,在第一象限内将△ABC放大,画出放大后的位似图形△A′B′C′;
(3)计算△A′B′C′的面积S.
19.(8分) 如图,在 ABCD中,E是CD的延长线上一点,连接BE交AD于点F,且AF=2FD.
(1)求证:△ABF∽△CEB;
(2)若△CEB的面积为9,求 ABCD的面积.
20.(10分) 如图,已知在梯形ABCD中,AD∥BC,AB⊥BC,∠AEB=∠ADC.
(1)求证:△ADE∽△DBC;
(2)连接EC,若CD2=AD·BC,求证:∠DCE=∠ADB.
21.(12分) 如图,在Rt△ABC中,∠C=90°,AC=10 cm,BC=8 cm.点P从点C出发,以2 cm/s的速度沿CA向点A匀速运动,同时点Q从点B出发,以1 cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一个点随之停止.
(1)经过几秒后,△PCQ的面积等于△ABC面积的?
(2)经过几秒后,△PCQ与△ABC相似?
22.(12分) 如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,=.
(1)当==时,求证△ABC∽△A′B′C′.证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A′B′C′是否相似,并说明理由.
参考答案
1-5DBBDB 6-10CBBCD
11.,-
12.8
13.(4,8)或(-4,-8)
14.1∶9
15.1. 05
16.①③④
17.解:∠α=118°,∠β=70°,x=6,y=12,z=6
18.解:(1)建立平面直角坐标系如图所示.点B的坐标为(3,2).
(2)如图所示.
(3)△A′B′C′的面积S为×4×8=16.
19.(1)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AB∥CD,∴∠ABF=∠E,∴△ABF∽△CEB.
(2)解:∵AF=2FD,∴AD=3FD.∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,AD=BC,∴△ABF∽△DEF,△CEB∽△DEF,∴S△ABF∶S△DEF=AF2∶FD2=4,S△CEB∶S△DEF=BC2∶FD2=AD2∶FD2=9.又∵△CEB的面积为9,∴△DEF的面积为1,△ABF的面积为4,∴ ABCD的面积为9-1+4=12.
20.证明:(1)∵AD∥BC,∴∠ADE=∠DBC,∠ADC+∠BCD=180°.∵∠AEB=∠ADC,∠AEB+∠AED=180°,∴∠AED=∠BCD,∴△ADE∽△DBC;
(2)由(1)可知△ADE∽△DBC,∴=,∴DB·DE=AD·BC.∵CD2=AD·BC,∴CD2=DB·DE,∴=.又∵∠CDE=∠BDC,∴△CDE∽△BDC,∴∠DCE=∠DBC.又∵∠ADB=∠DBC,∴∠DCE=∠ADB.
21.解:(1)设经过x秒后,△PCQ的面积等于△ABC面积的,由题意,得·2x·(8-x)=×10×8×,解得x1=x2=4,∴经过4秒后,△PCQ的面积等于△ABC面积的.(2)设经过t秒后,△PCQ与△ABC相似,∵∠C=∠C,∴分为两种情况:①=,即=,解得t=;②=,即=,解得t=.综上,经过秒或秒后,△PCQ与△ABC相似.
22. 解:(1)==;∠A=∠A′
(2)△ABC∽△A′B′C′.理由如下:如图,过点D,D′分别作DE∥BC,D′E′∥B′C′,DE交AC于点E,D′E′交A′C′于点E′.
∵DE∥BC,∴△ADE∽△ABC.∴==.同理,==.∵=,∴=.∴=.同理,=.∴=,即=.∴=.∵==,∴==.∴△DCE∽△D′C′E′.∴∠CED=∠C′E′D′.∵DE∥BC,∴∠CED+∠ACB=180°,同理,∠C′E′D′+∠A′C′B′=180°.∴∠ACB=∠A′C′B′.∵=,∴△ABC∽△A′B′C′.
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
2. 已知=,那么的值为( )
A. B. C. D.
3. 在比例尺为1:150 000的某城市地图上,若量得A、B两所学校的距离是4.2厘米,则A、B两所学校的实际距离是( )
A.630米 B.6 300米 C.8 400米 D.4 200米
4. 如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判定△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C
C.= D.=
5. 如图,在6×6的正方形网格中,连接两格点A,B,线段AB与网格线的交点为M,N,则AM∶MN∶NB为( )
A.3∶5∶4 B.1∶3∶2
C.1∶4∶2 D.3∶6∶5
6. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )
A.1.5 里 B.1.2 里
C.1.05 里 D.1.02 里
7. 如图,已知△ABC和△ADE均为等边三角形,点D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A.1 B.2 C.3 D.4
8. 如图,已知△OAB与△OA′B′是相似比为1∶2的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
A.(-x,-y) B.(-2x,-2y)
C.(-2x,2y) D.(2x,-2y)
9.如图,在边长为1 的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A.(0,0) B.(0,1) C.(-3,2) D.(3,-2)
10. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,4*6=24)
11. 已知=,则=__ __,=__ __.
12. 如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是__ __米.
13. 在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是__ __.
14. 如图,在△ABC中,E,F分别是边AB,AC上的点,且满足==,则△AEF与△ABC的面积比是________.
15.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB,AD的中点,GE⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=__ __里.
16.如图, ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①EO⊥AC;②S△AOD=4S△OCF;③AC∶BD=∶7;④FB2=OF·DF.其中正确的结论有__________(填写所有正确结论的序号).
三.解答题(共5小题, 56分)
17.(6分) 如图,已知梯形ABCD与梯形A′B′C′D′相似,求未知边x,y,z的长度和∠α,∠β的度数.
18.(8分) 如图,△ABC在方格纸(小正方形的边长均为1)中.
(1)请在方格纸上建立平面直角坐标系,使点A的坐标为(3,4),点C的坐标为(7,3),并求出点B的坐标;
(2)以原点O为位似中心,相似比为2?1,在第一象限内将△ABC放大,画出放大后的位似图形△A′B′C′;
(3)计算△A′B′C′的面积S.
19.(8分) 如图,在 ABCD中,E是CD的延长线上一点,连接BE交AD于点F,且AF=2FD.
(1)求证:△ABF∽△CEB;
(2)若△CEB的面积为9,求 ABCD的面积.
20.(10分) 如图,已知在梯形ABCD中,AD∥BC,AB⊥BC,∠AEB=∠ADC.
(1)求证:△ADE∽△DBC;
(2)连接EC,若CD2=AD·BC,求证:∠DCE=∠ADB.
21.(12分) 如图,在Rt△ABC中,∠C=90°,AC=10 cm,BC=8 cm.点P从点C出发,以2 cm/s的速度沿CA向点A匀速运动,同时点Q从点B出发,以1 cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一个点随之停止.
(1)经过几秒后,△PCQ的面积等于△ABC面积的?
(2)经过几秒后,△PCQ与△ABC相似?
22.(12分) 如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,=.
(1)当==时,求证△ABC∽△A′B′C′.证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A′B′C′是否相似,并说明理由.
参考答案
1-5DBBDB 6-10CBBCD
11.,-
12.8
13.(4,8)或(-4,-8)
14.1∶9
15.1. 05
16.①③④
17.解:∠α=118°,∠β=70°,x=6,y=12,z=6
18.解:(1)建立平面直角坐标系如图所示.点B的坐标为(3,2).
(2)如图所示.
(3)△A′B′C′的面积S为×4×8=16.
19.(1)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AB∥CD,∴∠ABF=∠E,∴△ABF∽△CEB.
(2)解:∵AF=2FD,∴AD=3FD.∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,AD=BC,∴△ABF∽△DEF,△CEB∽△DEF,∴S△ABF∶S△DEF=AF2∶FD2=4,S△CEB∶S△DEF=BC2∶FD2=AD2∶FD2=9.又∵△CEB的面积为9,∴△DEF的面积为1,△ABF的面积为4,∴ ABCD的面积为9-1+4=12.
20.证明:(1)∵AD∥BC,∴∠ADE=∠DBC,∠ADC+∠BCD=180°.∵∠AEB=∠ADC,∠AEB+∠AED=180°,∴∠AED=∠BCD,∴△ADE∽△DBC;
(2)由(1)可知△ADE∽△DBC,∴=,∴DB·DE=AD·BC.∵CD2=AD·BC,∴CD2=DB·DE,∴=.又∵∠CDE=∠BDC,∴△CDE∽△BDC,∴∠DCE=∠DBC.又∵∠ADB=∠DBC,∴∠DCE=∠ADB.
21.解:(1)设经过x秒后,△PCQ的面积等于△ABC面积的,由题意,得·2x·(8-x)=×10×8×,解得x1=x2=4,∴经过4秒后,△PCQ的面积等于△ABC面积的.(2)设经过t秒后,△PCQ与△ABC相似,∵∠C=∠C,∴分为两种情况:①=,即=,解得t=;②=,即=,解得t=.综上,经过秒或秒后,△PCQ与△ABC相似.
22. 解:(1)==;∠A=∠A′
(2)△ABC∽△A′B′C′.理由如下:如图,过点D,D′分别作DE∥BC,D′E′∥B′C′,DE交AC于点E,D′E′交A′C′于点E′.
∵DE∥BC,∴△ADE∽△ABC.∴==.同理,==.∵=,∴=.∴=.同理,=.∴=,即=.∴=.∵==,∴==.∴△DCE∽△D′C′E′.∴∠CED=∠C′E′D′.∵DE∥BC,∴∠CED+∠ACB=180°,同理,∠C′E′D′+∠A′C′B′=180°.∴∠ACB=∠A′C′B′.∵=,∴△ABC∽△A′B′C′.
