5.4抛体运动的规律计算题(word版含答案)
文档属性
| 名称 | 5.4抛体运动的规律计算题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-22 00:00:00 | ||
图片预览



文档简介
抛体运动的规律计算练习
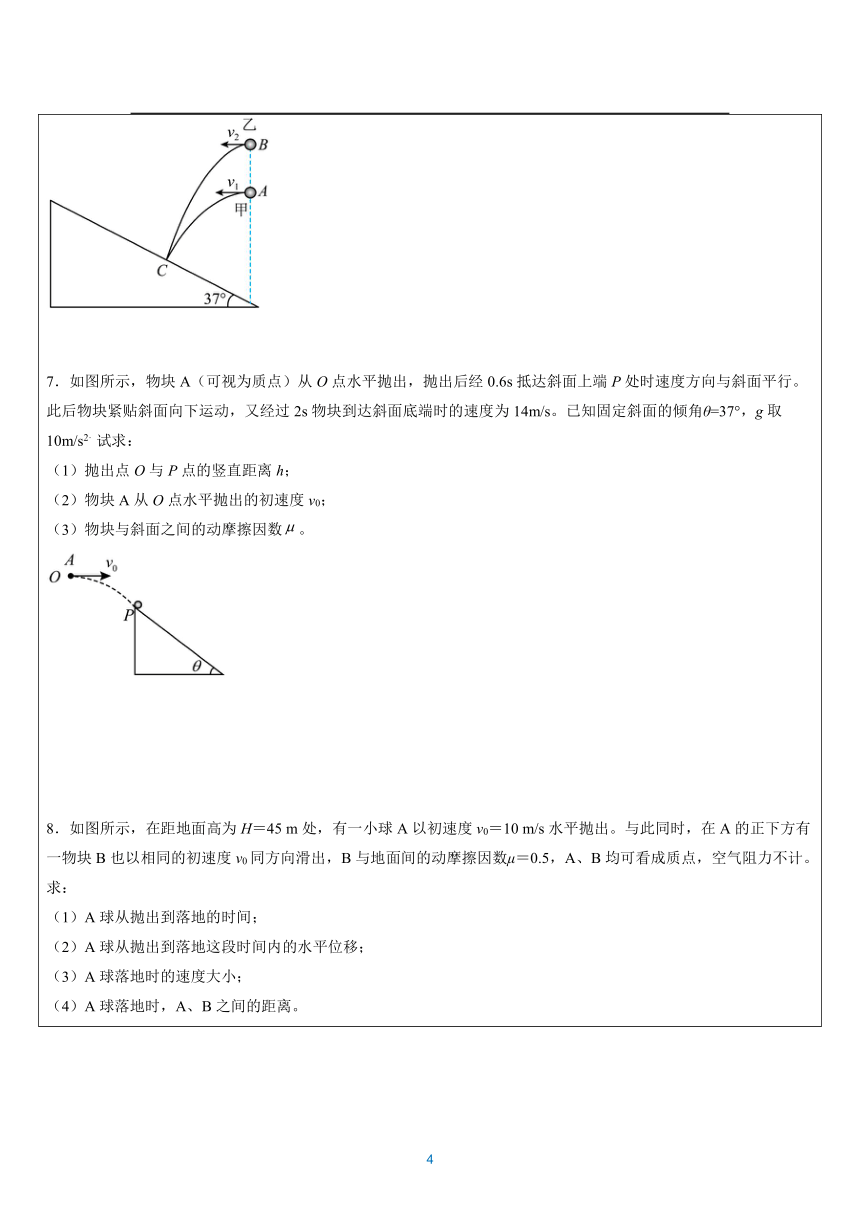
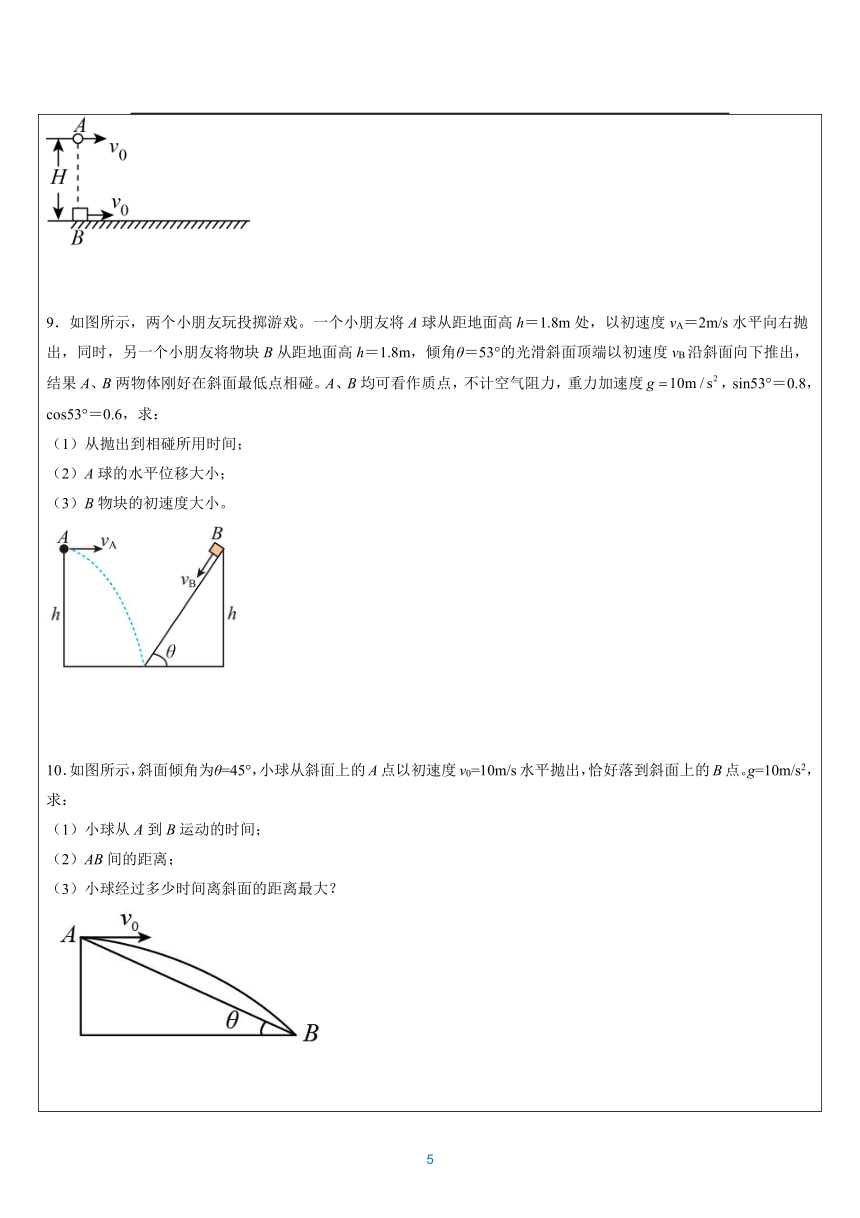
一.计算题 1.跑酷(Parkour)是时下风靡全球的时尚极限运动,跑酷可以强健体质,使得自身越发敏捷,反应能力更加迅速。某跑酷运动员,在水平高台上水平向右跑到高台边缘,以的速度从上边缘的A点水平向右跳出,运动时间后落在一倾角为 的斜面上的B点,速度方向与斜面垂直。此时运动员迅速转身并调整姿势,以的速度从B点水平向左蹬出,刚好落到斜面的底端C点。D点为平台的下边缘点,假设该运动员可视为质点,不计空气阻力,取,,。求: (1)运动员从高台边缘跳出的水平速度大小; (2)水平高台的高度H。 2.如图所示,一小滑块自平台上水平抛出,恰好落在一倾角为的固定斜面顶端,并刚好沿斜面下滑(与斜面无碰撞)。已知斜面顶端与平台的高度差,滑块与斜面间的动摩擦因数,重力加速度,,,求: (1)滑块水平抛出的初速度的大小? (2)若斜面顶端高,则滑块离开平台后经多长时间到达斜面底端? 3.如图所示,水平传送带装置两轮轴心间的水平距离L=8m,离地面高度h=3.2m。左边与传送带等高的光滑平台上,有一个可看成质点的小物体以v0=10m/s的初速度滑上传送带,从传送带的右端飞出做平抛运动,若物体与传送带间动摩擦因数μ=0.6,g=10m/s2,求: (1)若传送带保持静止,物体从传送带上抛出后的水平位移x1; (2)若传送带以v1=15m/s顺时针匀速转动,物体从传送带上抛出后的水平位移x2。 4.2022年第24届冬季奥林匹克运动会将在北京和张家口举行,跳台滑雪是其中最具观赏性的项目之一。如图所示为简化的跳台滑雪的雪道示意图,AO为助滑道,OB为着陆坡。运动员从助滑道上的A点由静止滑下,然后从O点沿水平方向飞出,最后在着陆坡上着陆。已知,着陆坡OB的倾角为37°,O点与着陆点间的距离为75m,重力加速度g取,,。将运动员和滑雪板整体看作质点,不计一切摩擦和空气阻力,求: (1)运动员从O点飞出到着陆的时间t; (2)运动员经过O点时的速度大小v; (3)A点与O点的高度差h。 5.跑酷(Pakour)是时下风靡全球的时尚极限运动,一跑酷运动员在一次训练中的运动可简化为以下运动:运动员首先在平直高台上以4m/s2的加速度从静止开始匀加速运动,运动8m的位移后,在距地面高为5m的高台边缘水平跳出,在空中调整姿势后恰好垂直落在一倾角为53°的斜面中点位置。此后运动员迅速调整姿势沿水平方向蹬出,假设该运动员可视为质点,不计空气阻力,取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6,求: (1)运动员从楼顶边缘跳出到落到斜面上所用的时间t; (2)该斜面底端与高台边缘的水平距离s; (3)若运动员水平蹬出斜面后落在地面上,求运动员的蹬出速度范围。 6.如图所示,小球甲以水平初速度v1从A点水平抛出,小球乙以水平初速度v2从B点水平抛出,两球的落点都在倾角为37°斜面的C点,B点在A点的正上方;甲落在C点时,速度正好与斜面垂直;乙落在C点时,其位移BC正好与斜面垂直;不计空气的阻力,已知乙的初速度v2=1.5m/s,g=10m/s2,tan37°=,求: (1)甲的水平位移大小和乙的位移大小; (2)B、A两点的高度差。 7.如图所示,物块A(可视为质点)从O点水平抛出,抛出后经0.6s抵达斜面上端P处时速度方向与斜面平行。此后物块紧贴斜面向下运动,又经过2s物块到达斜面底端时的速度为14m/s。已知固定斜面的倾角θ=37°,g取10m/s2.试求: (1)抛出点O与P点的竖直距离h; (2)物块A从O点水平抛出的初速度v0; (3)物块与斜面之间的动摩擦因数。 8.如图所示,在距地面高为H=45 m处,有一小球A以初速度v0=10 m/s水平抛出。与此同时,在A的正下方有一物块B也以相同的初速度v0同方向滑出,B与地面间的动摩擦因数μ=0.5,A、B均可看成质点,空气阻力不计。求: (1)A球从抛出到落地的时间; (2)A球从抛出到落地这段时间内的水平位移; (3)A球落地时的速度大小; (4)A球落地时,A、B之间的距离。 9.如图所示,两个小朋友玩投掷游戏。一个小朋友将A球从距地面高h=1.8m处,以初速度vA=2m/s水平向右抛出,同时,另一个小朋友将物块B从距地面高h=1.8m,倾角θ=53°的光滑斜面顶端以初速度vB沿斜面向下推出,结果A、B两物体刚好在斜面最低点相碰。A、B均可看作质点,不计空气阻力,重力加速度,sin53°=0.8,cos53°=0.6,求: (1)从抛出到相碰所用时间; (2)A球的水平位移大小; (3)B物块的初速度大小。 10.如图所示,斜面倾角为θ=45°,小球从斜面上的A点以初速度v0=10m/s水平抛出,恰好落到斜面上的B点。g=10m/s2,求: (1)小球从A到B运动的时间; (2)AB间的距离; (3)小球经过多少时间离斜面的距离最大? 11.如图甲所示,在高的平台上,一名质量的滑板运动员(可视为质点),在距平台右边处以一初速度v0向右运动,在平台运动的v2-x关系如图乙所示,到达平台右边时做平抛运动,落在地面时与平台右边的水平距离,取,求 (1)滑板运动员平抛时的初速度v的大小; (2)滑板运动员在平台滑动过程所受的摩擦力f的大小; (3)滑板运动员的初速度v0的大小。 12.飞镖是常见的一种娱乐活动,如图所示,靶盘竖直放置,A、O两点等高且相距4m,将飞镖从点A沿AO方向掷出,经0.2s落在靶心正下方的点B不计空气阻力,重力加速度g=10,求: (1)飞镖从点A抛出时的速度。 (2)飞镖落点B与靶心O的距离。 (3)如果要让飞镖命中靶心O,根据本题所给的条件,应如何调整投掷飞镖的方法? 13.甲、乙两名同学在操场上用两个篮球(可视为质点)玩“空中击球”游戏,如图所示,甲同学在O点将篮球A以速度v斜向上抛出,使得篮球能够从乙同学正上方经过,乙同学选择合适时机,将篮球B从与O点等高的Q点以的初速度竖直向上抛出,篮球A经过最高点M后,在下降过程中经过P点时被正在上升的篮球B恰好击中,N位于连线上且在M点正下方,已知O、N两点距离,N、Q两点距离,P、Q两点距离,不计空气阻力,重力加速度,求: (1)篮球A抛出的初速度v; (2)篮球B延迟于篮球A多长时间抛出? 14.摩托车飞越表演是一项惊险刺激的活动。假设在一次飞越河流的表演中,摩托车以72km/h的水平速度离开平台,成功落到对面的平台上,测得两岸平台的高度差为5m,如图所示,若飞越过程中不计空气阻力,摩托车可以看成质点,重力加速度g=10m/s2,求: (1)摩托车在空中的时长; (2)河流的最大宽度; (3)摩托车落地瞬间的速度。 15.某射击队进行某项模拟训练时使用的装置如图所示,受训运动员处于高度H=20m的塔顶,在距塔水平距离l=100m的地面上有一个电子抛靶装置,圆形靶以某一速度被装置竖直向上抛出。在靶被抛出的同时,运动员立即持枪沿水平方向射击,子弹的初速度v1=100m/s。若子弹沿水平方向射出,恰能击中抛靶(仍在上升),不计人的反应时间,抛靶可以看成质点,取重力加速度处g=10m/s2,不计空气阻力,求∶ (1)子弹击中靶时,靶距地面的高度h; (2)靶被抛出时的速度大小v2。 16.风洞实验是测试飞行器性能的重要方法,风洞中可以提供大小和方向恒定的风力。在某风洞中存在水平方向的恒定风力,将质量为m的小球以速度v0从O点斜向上弹射出去,v0与水平方向夹角为θ,经过一段时间后,小球到达射出点正上方的P点时,速度恰好为水平方向,重力加速度为g。求: (1)P点到O点的竖直高度h; (2)水平风力的大小F; (3)到达P点时速度的大小vp。 17.如图所示,一位网球运动员以拍击球,使网球沿水平方向飞出。第一个球飞出时的初速度为v1,落在自己一方场地上后弹跳起来,刚好擦网而过,并落在对方场地的A点处。第二个球飞出时的初速度为v2,直接擦网而过,也落在A点处。设球与地面碰撞时没有能量损失,且不计空气阻力,求: (1)网球两次飞出时的初速度之比v1:v2; (2)运动员击球点的高度H与网高h之比H:h。 18.如图所示,枪管对准小球C,在同一水平线上。子弹射出枪口时,悬挂小球的细线突然断开,小球C由静止开始下落。已知的距离s为,不计空气阻力,重力加速度g取,问: (1)如果小球C下落时被击中,那么子弹离开枪口时的速度是多大; (2)如果子弹离开枪口时的速度大于上面所求的数值,那么子弹仍然能击中这个小球吗,为什么; (3)如果悬挂小球的细线突然断开后,小球C不是由静止开始下落,而是和子弹同时以的初速度沿子弹初速度方向水平抛出,那么子弹是否还能击中这个小球;若能击中,在何处击中。 19.某电视台娱乐节目,要求选手要从较高的平台上以水平速度跃出后,落在水平传送带上,已知平台与传送带高度差,水池宽度,传送带AB间的距离,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个反应时间后,立刻以,方向向右的加速度跑至传送带最右端。 (1)若传送带静止,选手以水平速度从平台跃出,求从开始跃出到跑至传送带右端经历时间。 (2)若传送带以的恒定速度向左运动,选手若要能到达传送带右端,则从高台上跃出的水平速度至少多大? 20.2020年2月,在国际单板滑雪U型场地赛中,我国运动员蔡雪桐勇夺冠军。如图,滑道边缘线的倾角,运动员以速度从上的O点沿的切面滑出滑道,滑出时速度方向与的夹角为,腾空后从上的A点进入滑道。已知重力加速度为g,运动员可视为质点,不计空气阻力。求运动员: (1)腾空中上升的最大高度; (2)腾空中离的最大距离; (3)到达A点时的速度。 参考答案 1.(1)8m/s;(2)5.0m 【解析】 (1)在B点有 联立解得 (2)从B点跳到斜面的底端C点,有 解得 水平高台的高度H,则有 2.(1);(2) 【解析】 (1)滑块做平抛运动,落在斜面顶端时的竖直分速度设为vy,则有 在斜面顶端,把滑块速度分解,则有 (2)滑块到达斜面顶端之前的运动时间设为t1,有 解得 根据分速度与合速度的关系,可得滑块在斜面顶端时,沿斜面下滑的初速度为 由牛顿第二定律,可得 解得 结合几何关系,由运动学公式可得 解得 离开平台后,到达斜面底端的总时间为 3.(1)1.6m;(2)11.2m 【解析】 (1)对物块,在传送带上减速滑动过程 解得 根据 解得 平抛过程 解得 水平位移 (2)由于 物块滑上传送带上后先加速运动,假设一直匀加速 解得 故假设成立 物块第二次抛出的位移 4.(1);(2);(3) 【解析】 (1)运动员在OB上点着陆,则,运动员从O点沿水平方向飞出,最后在着陆坡上着陆,竖直方向 解得 (2)运动员从O点沿水平方向飞出,最后在着陆坡上着陆,水平方向 解得 (3)运动员从助滑道上的A点由静止滑下到O点的过程中,根据能量守恒 解得 5.(1)0.6s;(2)2.4m;(3)3m/s≤v0′≤6m/s 【解析】 (1)设运动员从高台边缘水平跳出的速度为v0,匀加速的位移为l,由速度位移公式得 =2al 代入数据解得 v0=8m/s 恰好垂直落在一倾角为53°的斜面中点位置时,由运动的合成与分解得 tan53°= 代入数据解得运动员从楼顶边缘跳出到落到斜面上所用的时间为 t=0.6s (2)设高台距斜面中点的水平距离为x,水平方向上有 x=v0t=8×0.6m=4.8m 竖直方向上,有 y=m=1.8m 则斜面中点距地面竖直距离为 斜面中点距斜面底端水平距离为 x′=m=2.4m 该斜面底端与高台边缘的水平距离为 (3)根据位移时间公式,可得运动员水平蹬出斜面后落在地面上的时间为 t′=s=0.8s 能落到地面上,水平位移的范围为 2.4m≤x′≤4.8m 根据运动学公式得 x′=v0′t′ 代入数据解得运动员的蹬出速度范围为 3m/s≤v0′≤6m/s 6.(1)0.6m,1m;(2)0.4m 【解析】 (1)设乙的运动时间为,乙的位移BC正好与斜面垂直,把BC分别沿水平方向和竖直方向分解,由几何关系有 结合,解得 乙的水平位移 甲、乙的水平位移相等 设乙的位移,由几何关系 综合可得 , (2)设甲的运动时间为,甲落在C点时,速度正好与斜面垂直,把甲在C点的速度分别沿水平方向和竖直方向分解,由几何关系有 甲的水平位移 B、A两点的高度差 综合可得 7.(1);(2);(3) 【解析】 (1)物体A竖直方向做自由落体运动,则有 (2)物体A竖直方向做自由落体运动,则有 故有 (3)由题意可知 由运动学方程有 在斜面上,受力分析可得 解得 联立解得 8.(1)3 s;(2)30 m;(3);(4)20 m 【解析】 (1)A球抛出后做平抛运动,竖直方向有 解得 (2)A球从抛出到落地的水平位移 xA=v0t=30 m (3)A球落地时的竖直方向速度大小为 则落地时的速度大小为 (4)物块B做匀减速直线运动,由牛顿第二定律可得 解得 a=5 m/s2 物块B滑动的时间 在此期间B运动的距离 所以A球落地时,A、B之间的距离 xAB=xA-xB=20 m 9.(1)0.6s;(2)1.2m;(3)1.35m/s 【解析】 (1)A球在竖直方向做自由落体运动,则 解得 (2)A球在水平方向做匀速直线运动 (3)B物块在斜面上的加速度 B物体在斜面上的位移 根据运动学公式 可得 10.(1);(2);(3) 【解析】 (1)小球从A点平抛落在B点,有 而平抛的位移偏向角为,有 联立解得 , (2)AB间的距离为 (3)当平抛的速度与斜面平行时,小球离斜面最远,设时间为,有 解得 11.(1)4m/s;(2)125 N;(3) 6m/s 【解析】 (1)小木块从平台滑出后做平抛运动,有 得 木块飞出时的速度 (2)因为小木块在平台上滑动过程中做匀减速运动,设加速度大小为a,根据 整理得 根据图像得 解得 根据牛顿第二定律,得摩擦力大小 (3)根据运动学公式 解得 12.(1)20m/s;(2)0.2m;(3)保持飞镖的初速度不变,抛出点向上移动0.2m 【解析】 (1)飞镖做平抛运动,水平方向做匀速运动,则从点A抛出时的速度 (2)竖直方向做自由落体运动,则飞镖落点B与靶心O的距离 (3)如果要让飞镖命中靶心O,根据本题所给的条件,应该保持飞镖的初速度不变,抛出点向上移动0.2m。 13.(1)15m/s;(2)0.8s 【解析】 (1)设M、N间距为H,篮球A抛出的初速度为v,其水平和竖直分速度分别为vx和vy则有 ① ② ③ ④ ⑤ ⑥ 由①②③④⑤⑥可解得 v=15m/s,t1=1.2s,t2=0.4s (2)B球上抛过程有 解得 t3=0.8或t3=1.6s(舍去) 篮球B延迟于篮球A的时间 14.(1)1s;(2)20m;(3) 【解析】 (1)根据平抛运动竖直距离与时间关系得 解得 t=1s (2)水平方向初速度 v0=72km/h=20m/s 河流最大宽度为 x=v0t=20m (3)落地时竖直速度为 vy=gt=10m/s 由速度的合成得 15.(1)15m;(2)20m/s 【解析】 (1)若靶能被击中,则击中处应在抛靶装置的正上方,设经历的时间为t,则有 l=v1t 解得 子弹下降的高度为 靶距地面的高度为 (2)根据竖直上抛运动公式,可得 代入数据,解得 v2=20m/s 16.(1);(2);(3) 【解析】 (1)将此运动分解成水平方向与竖直方向两分运动,依据运动学公式与矢量合成法则,那么竖直方向 vy=v0sinθ h= (2)水平方向上有 vx=v0cosθ 由牛顿第二定律得 ax= 且 t= vx=ax 可解得 F= (3)P点时,速度恰好为水平方向,即竖直方向速度为零,得 vp=v0x=v0cosθ 17.(1)1:3;(2)4:3 【解析】 (1)两球被击出后都做平抛运动,由平抛运动的规律可知,两球分别被击出至各自第一次落地的时间是相等的。 由题意知水平射程之比为 x1:x2=1:3 故平抛运动的初速度之比为 v1:v2=1:3 (2)第一个球落地后反弹做斜抛运动,根据运动的对称性可知,DB段和OB段是相同的平抛运动,则两球下落相同高度(H-h)后水平距离之和为 x1′+x2′=2x1 而 x1=v1t1,x1′=v1t2,x2′=v2t2 联立可得 t1=2t2 根据公式得 即 H=4(H-h) 解得 H:h=4:3 18.(1)50m/s;(2)见解析;(3)见解析 【解析】 (1)子弹射出枪口后做平抛运动,小球C做自由落体运动,两者在竖直方向的运动相同,小球C下落20m时被击中,则有 解得 这段时间内,子弹水平匀速运动了s=100m,根据 解得 (2)如果子弹离开枪口时的速度大于上面所求的数值,由于子弹和小球在竖直方向运动相同,则子弹仍可以击中小球,并且击中时间缩短。 (3)如果悬挂小球的细线突然断开后,小球C不是由静止开始下落,而是和子弹同时以10m/s的初速度沿子弹初速度方向水平抛出,则子弹和小球均做平抛运动,竖直方向上运动情况相同,水平方向上,两者都做匀速直线运动,子弹的速度大,可以击中小球。水平方向上 解得 竖直方向上 水平方向上 即在子弹射出后2.5s击中,位置在小球C的原始悬挂点右侧水平距离25m,竖直距离31.25m处。 19.(1)4.9s;(2) 【解析】 (1)平抛运动过程有 选手在水平方向上的位移 则匀加速运动的位移 解得 所以总时间 (2)设水平跃出速度为,落到传送带反应时间内向左位移大小 然后向左减速至速度为零,向左发生位移 不从传送带上掉下,平抛水平位移 所以 所以最小速度为。 20.(1);(2);(3),与斜面的夹角为 【解析】 (1)将初速度为沿竖直方向分解得 由公式得 解得竖直方向上升的最大高度为 (2)经分析,当速度方向与斜面PQ平行时离斜面距离最大,将初速度和加速度分别分解在沿斜面方向和垂直斜面方向,则沿斜面方向有 , 垂直斜面方向有 , 运动员腾空中离PQ的最大距离为H,则有 解得 (3)设运动员从O点到离PQ最远的时间为t,则有 运动员再滑入轨道时,垂直斜面方向的速度大小不变,仍为 沿斜面向下的速度为 则到达A点时的速度大小为 到达A点时的速度方向与斜面的夹角正切值为 解得
1
一.计算题 1.跑酷(Parkour)是时下风靡全球的时尚极限运动,跑酷可以强健体质,使得自身越发敏捷,反应能力更加迅速。某跑酷运动员,在水平高台上水平向右跑到高台边缘,以的速度从上边缘的A点水平向右跳出,运动时间后落在一倾角为 的斜面上的B点,速度方向与斜面垂直。此时运动员迅速转身并调整姿势,以的速度从B点水平向左蹬出,刚好落到斜面的底端C点。D点为平台的下边缘点,假设该运动员可视为质点,不计空气阻力,取,,。求: (1)运动员从高台边缘跳出的水平速度大小; (2)水平高台的高度H。 2.如图所示,一小滑块自平台上水平抛出,恰好落在一倾角为的固定斜面顶端,并刚好沿斜面下滑(与斜面无碰撞)。已知斜面顶端与平台的高度差,滑块与斜面间的动摩擦因数,重力加速度,,,求: (1)滑块水平抛出的初速度的大小? (2)若斜面顶端高,则滑块离开平台后经多长时间到达斜面底端? 3.如图所示,水平传送带装置两轮轴心间的水平距离L=8m,离地面高度h=3.2m。左边与传送带等高的光滑平台上,有一个可看成质点的小物体以v0=10m/s的初速度滑上传送带,从传送带的右端飞出做平抛运动,若物体与传送带间动摩擦因数μ=0.6,g=10m/s2,求: (1)若传送带保持静止,物体从传送带上抛出后的水平位移x1; (2)若传送带以v1=15m/s顺时针匀速转动,物体从传送带上抛出后的水平位移x2。 4.2022年第24届冬季奥林匹克运动会将在北京和张家口举行,跳台滑雪是其中最具观赏性的项目之一。如图所示为简化的跳台滑雪的雪道示意图,AO为助滑道,OB为着陆坡。运动员从助滑道上的A点由静止滑下,然后从O点沿水平方向飞出,最后在着陆坡上着陆。已知,着陆坡OB的倾角为37°,O点与着陆点间的距离为75m,重力加速度g取,,。将运动员和滑雪板整体看作质点,不计一切摩擦和空气阻力,求: (1)运动员从O点飞出到着陆的时间t; (2)运动员经过O点时的速度大小v; (3)A点与O点的高度差h。 5.跑酷(Pakour)是时下风靡全球的时尚极限运动,一跑酷运动员在一次训练中的运动可简化为以下运动:运动员首先在平直高台上以4m/s2的加速度从静止开始匀加速运动,运动8m的位移后,在距地面高为5m的高台边缘水平跳出,在空中调整姿势后恰好垂直落在一倾角为53°的斜面中点位置。此后运动员迅速调整姿势沿水平方向蹬出,假设该运动员可视为质点,不计空气阻力,取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6,求: (1)运动员从楼顶边缘跳出到落到斜面上所用的时间t; (2)该斜面底端与高台边缘的水平距离s; (3)若运动员水平蹬出斜面后落在地面上,求运动员的蹬出速度范围。 6.如图所示,小球甲以水平初速度v1从A点水平抛出,小球乙以水平初速度v2从B点水平抛出,两球的落点都在倾角为37°斜面的C点,B点在A点的正上方;甲落在C点时,速度正好与斜面垂直;乙落在C点时,其位移BC正好与斜面垂直;不计空气的阻力,已知乙的初速度v2=1.5m/s,g=10m/s2,tan37°=,求: (1)甲的水平位移大小和乙的位移大小; (2)B、A两点的高度差。 7.如图所示,物块A(可视为质点)从O点水平抛出,抛出后经0.6s抵达斜面上端P处时速度方向与斜面平行。此后物块紧贴斜面向下运动,又经过2s物块到达斜面底端时的速度为14m/s。已知固定斜面的倾角θ=37°,g取10m/s2.试求: (1)抛出点O与P点的竖直距离h; (2)物块A从O点水平抛出的初速度v0; (3)物块与斜面之间的动摩擦因数。 8.如图所示,在距地面高为H=45 m处,有一小球A以初速度v0=10 m/s水平抛出。与此同时,在A的正下方有一物块B也以相同的初速度v0同方向滑出,B与地面间的动摩擦因数μ=0.5,A、B均可看成质点,空气阻力不计。求: (1)A球从抛出到落地的时间; (2)A球从抛出到落地这段时间内的水平位移; (3)A球落地时的速度大小; (4)A球落地时,A、B之间的距离。 9.如图所示,两个小朋友玩投掷游戏。一个小朋友将A球从距地面高h=1.8m处,以初速度vA=2m/s水平向右抛出,同时,另一个小朋友将物块B从距地面高h=1.8m,倾角θ=53°的光滑斜面顶端以初速度vB沿斜面向下推出,结果A、B两物体刚好在斜面最低点相碰。A、B均可看作质点,不计空气阻力,重力加速度,sin53°=0.8,cos53°=0.6,求: (1)从抛出到相碰所用时间; (2)A球的水平位移大小; (3)B物块的初速度大小。 10.如图所示,斜面倾角为θ=45°,小球从斜面上的A点以初速度v0=10m/s水平抛出,恰好落到斜面上的B点。g=10m/s2,求: (1)小球从A到B运动的时间; (2)AB间的距离; (3)小球经过多少时间离斜面的距离最大? 11.如图甲所示,在高的平台上,一名质量的滑板运动员(可视为质点),在距平台右边处以一初速度v0向右运动,在平台运动的v2-x关系如图乙所示,到达平台右边时做平抛运动,落在地面时与平台右边的水平距离,取,求 (1)滑板运动员平抛时的初速度v的大小; (2)滑板运动员在平台滑动过程所受的摩擦力f的大小; (3)滑板运动员的初速度v0的大小。 12.飞镖是常见的一种娱乐活动,如图所示,靶盘竖直放置,A、O两点等高且相距4m,将飞镖从点A沿AO方向掷出,经0.2s落在靶心正下方的点B不计空气阻力,重力加速度g=10,求: (1)飞镖从点A抛出时的速度。 (2)飞镖落点B与靶心O的距离。 (3)如果要让飞镖命中靶心O,根据本题所给的条件,应如何调整投掷飞镖的方法? 13.甲、乙两名同学在操场上用两个篮球(可视为质点)玩“空中击球”游戏,如图所示,甲同学在O点将篮球A以速度v斜向上抛出,使得篮球能够从乙同学正上方经过,乙同学选择合适时机,将篮球B从与O点等高的Q点以的初速度竖直向上抛出,篮球A经过最高点M后,在下降过程中经过P点时被正在上升的篮球B恰好击中,N位于连线上且在M点正下方,已知O、N两点距离,N、Q两点距离,P、Q两点距离,不计空气阻力,重力加速度,求: (1)篮球A抛出的初速度v; (2)篮球B延迟于篮球A多长时间抛出? 14.摩托车飞越表演是一项惊险刺激的活动。假设在一次飞越河流的表演中,摩托车以72km/h的水平速度离开平台,成功落到对面的平台上,测得两岸平台的高度差为5m,如图所示,若飞越过程中不计空气阻力,摩托车可以看成质点,重力加速度g=10m/s2,求: (1)摩托车在空中的时长; (2)河流的最大宽度; (3)摩托车落地瞬间的速度。 15.某射击队进行某项模拟训练时使用的装置如图所示,受训运动员处于高度H=20m的塔顶,在距塔水平距离l=100m的地面上有一个电子抛靶装置,圆形靶以某一速度被装置竖直向上抛出。在靶被抛出的同时,运动员立即持枪沿水平方向射击,子弹的初速度v1=100m/s。若子弹沿水平方向射出,恰能击中抛靶(仍在上升),不计人的反应时间,抛靶可以看成质点,取重力加速度处g=10m/s2,不计空气阻力,求∶ (1)子弹击中靶时,靶距地面的高度h; (2)靶被抛出时的速度大小v2。 16.风洞实验是测试飞行器性能的重要方法,风洞中可以提供大小和方向恒定的风力。在某风洞中存在水平方向的恒定风力,将质量为m的小球以速度v0从O点斜向上弹射出去,v0与水平方向夹角为θ,经过一段时间后,小球到达射出点正上方的P点时,速度恰好为水平方向,重力加速度为g。求: (1)P点到O点的竖直高度h; (2)水平风力的大小F; (3)到达P点时速度的大小vp。 17.如图所示,一位网球运动员以拍击球,使网球沿水平方向飞出。第一个球飞出时的初速度为v1,落在自己一方场地上后弹跳起来,刚好擦网而过,并落在对方场地的A点处。第二个球飞出时的初速度为v2,直接擦网而过,也落在A点处。设球与地面碰撞时没有能量损失,且不计空气阻力,求: (1)网球两次飞出时的初速度之比v1:v2; (2)运动员击球点的高度H与网高h之比H:h。 18.如图所示,枪管对准小球C,在同一水平线上。子弹射出枪口时,悬挂小球的细线突然断开,小球C由静止开始下落。已知的距离s为,不计空气阻力,重力加速度g取,问: (1)如果小球C下落时被击中,那么子弹离开枪口时的速度是多大; (2)如果子弹离开枪口时的速度大于上面所求的数值,那么子弹仍然能击中这个小球吗,为什么; (3)如果悬挂小球的细线突然断开后,小球C不是由静止开始下落,而是和子弹同时以的初速度沿子弹初速度方向水平抛出,那么子弹是否还能击中这个小球;若能击中,在何处击中。 19.某电视台娱乐节目,要求选手要从较高的平台上以水平速度跃出后,落在水平传送带上,已知平台与传送带高度差,水池宽度,传送带AB间的距离,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个反应时间后,立刻以,方向向右的加速度跑至传送带最右端。 (1)若传送带静止,选手以水平速度从平台跃出,求从开始跃出到跑至传送带右端经历时间。 (2)若传送带以的恒定速度向左运动,选手若要能到达传送带右端,则从高台上跃出的水平速度至少多大? 20.2020年2月,在国际单板滑雪U型场地赛中,我国运动员蔡雪桐勇夺冠军。如图,滑道边缘线的倾角,运动员以速度从上的O点沿的切面滑出滑道,滑出时速度方向与的夹角为,腾空后从上的A点进入滑道。已知重力加速度为g,运动员可视为质点,不计空气阻力。求运动员: (1)腾空中上升的最大高度; (2)腾空中离的最大距离; (3)到达A点时的速度。 参考答案 1.(1)8m/s;(2)5.0m 【解析】 (1)在B点有 联立解得 (2)从B点跳到斜面的底端C点,有 解得 水平高台的高度H,则有 2.(1);(2) 【解析】 (1)滑块做平抛运动,落在斜面顶端时的竖直分速度设为vy,则有 在斜面顶端,把滑块速度分解,则有 (2)滑块到达斜面顶端之前的运动时间设为t1,有 解得 根据分速度与合速度的关系,可得滑块在斜面顶端时,沿斜面下滑的初速度为 由牛顿第二定律,可得 解得 结合几何关系,由运动学公式可得 解得 离开平台后,到达斜面底端的总时间为 3.(1)1.6m;(2)11.2m 【解析】 (1)对物块,在传送带上减速滑动过程 解得 根据 解得 平抛过程 解得 水平位移 (2)由于 物块滑上传送带上后先加速运动,假设一直匀加速 解得 故假设成立 物块第二次抛出的位移 4.(1);(2);(3) 【解析】 (1)运动员在OB上点着陆,则,运动员从O点沿水平方向飞出,最后在着陆坡上着陆,竖直方向 解得 (2)运动员从O点沿水平方向飞出,最后在着陆坡上着陆,水平方向 解得 (3)运动员从助滑道上的A点由静止滑下到O点的过程中,根据能量守恒 解得 5.(1)0.6s;(2)2.4m;(3)3m/s≤v0′≤6m/s 【解析】 (1)设运动员从高台边缘水平跳出的速度为v0,匀加速的位移为l,由速度位移公式得 =2al 代入数据解得 v0=8m/s 恰好垂直落在一倾角为53°的斜面中点位置时,由运动的合成与分解得 tan53°= 代入数据解得运动员从楼顶边缘跳出到落到斜面上所用的时间为 t=0.6s (2)设高台距斜面中点的水平距离为x,水平方向上有 x=v0t=8×0.6m=4.8m 竖直方向上,有 y=m=1.8m 则斜面中点距地面竖直距离为 斜面中点距斜面底端水平距离为 x′=m=2.4m 该斜面底端与高台边缘的水平距离为 (3)根据位移时间公式,可得运动员水平蹬出斜面后落在地面上的时间为 t′=s=0.8s 能落到地面上,水平位移的范围为 2.4m≤x′≤4.8m 根据运动学公式得 x′=v0′t′ 代入数据解得运动员的蹬出速度范围为 3m/s≤v0′≤6m/s 6.(1)0.6m,1m;(2)0.4m 【解析】 (1)设乙的运动时间为,乙的位移BC正好与斜面垂直,把BC分别沿水平方向和竖直方向分解,由几何关系有 结合,解得 乙的水平位移 甲、乙的水平位移相等 设乙的位移,由几何关系 综合可得 , (2)设甲的运动时间为,甲落在C点时,速度正好与斜面垂直,把甲在C点的速度分别沿水平方向和竖直方向分解,由几何关系有 甲的水平位移 B、A两点的高度差 综合可得 7.(1);(2);(3) 【解析】 (1)物体A竖直方向做自由落体运动,则有 (2)物体A竖直方向做自由落体运动,则有 故有 (3)由题意可知 由运动学方程有 在斜面上,受力分析可得 解得 联立解得 8.(1)3 s;(2)30 m;(3);(4)20 m 【解析】 (1)A球抛出后做平抛运动,竖直方向有 解得 (2)A球从抛出到落地的水平位移 xA=v0t=30 m (3)A球落地时的竖直方向速度大小为 则落地时的速度大小为 (4)物块B做匀减速直线运动,由牛顿第二定律可得 解得 a=5 m/s2 物块B滑动的时间 在此期间B运动的距离 所以A球落地时,A、B之间的距离 xAB=xA-xB=20 m 9.(1)0.6s;(2)1.2m;(3)1.35m/s 【解析】 (1)A球在竖直方向做自由落体运动,则 解得 (2)A球在水平方向做匀速直线运动 (3)B物块在斜面上的加速度 B物体在斜面上的位移 根据运动学公式 可得 10.(1);(2);(3) 【解析】 (1)小球从A点平抛落在B点,有 而平抛的位移偏向角为,有 联立解得 , (2)AB间的距离为 (3)当平抛的速度与斜面平行时,小球离斜面最远,设时间为,有 解得 11.(1)4m/s;(2)125 N;(3) 6m/s 【解析】 (1)小木块从平台滑出后做平抛运动,有 得 木块飞出时的速度 (2)因为小木块在平台上滑动过程中做匀减速运动,设加速度大小为a,根据 整理得 根据图像得 解得 根据牛顿第二定律,得摩擦力大小 (3)根据运动学公式 解得 12.(1)20m/s;(2)0.2m;(3)保持飞镖的初速度不变,抛出点向上移动0.2m 【解析】 (1)飞镖做平抛运动,水平方向做匀速运动,则从点A抛出时的速度 (2)竖直方向做自由落体运动,则飞镖落点B与靶心O的距离 (3)如果要让飞镖命中靶心O,根据本题所给的条件,应该保持飞镖的初速度不变,抛出点向上移动0.2m。 13.(1)15m/s;(2)0.8s 【解析】 (1)设M、N间距为H,篮球A抛出的初速度为v,其水平和竖直分速度分别为vx和vy则有 ① ② ③ ④ ⑤ ⑥ 由①②③④⑤⑥可解得 v=15m/s,t1=1.2s,t2=0.4s (2)B球上抛过程有 解得 t3=0.8或t3=1.6s(舍去) 篮球B延迟于篮球A的时间 14.(1)1s;(2)20m;(3) 【解析】 (1)根据平抛运动竖直距离与时间关系得 解得 t=1s (2)水平方向初速度 v0=72km/h=20m/s 河流最大宽度为 x=v0t=20m (3)落地时竖直速度为 vy=gt=10m/s 由速度的合成得 15.(1)15m;(2)20m/s 【解析】 (1)若靶能被击中,则击中处应在抛靶装置的正上方,设经历的时间为t,则有 l=v1t 解得 子弹下降的高度为 靶距地面的高度为 (2)根据竖直上抛运动公式,可得 代入数据,解得 v2=20m/s 16.(1);(2);(3) 【解析】 (1)将此运动分解成水平方向与竖直方向两分运动,依据运动学公式与矢量合成法则,那么竖直方向 vy=v0sinθ h= (2)水平方向上有 vx=v0cosθ 由牛顿第二定律得 ax= 且 t= vx=ax 可解得 F= (3)P点时,速度恰好为水平方向,即竖直方向速度为零,得 vp=v0x=v0cosθ 17.(1)1:3;(2)4:3 【解析】 (1)两球被击出后都做平抛运动,由平抛运动的规律可知,两球分别被击出至各自第一次落地的时间是相等的。 由题意知水平射程之比为 x1:x2=1:3 故平抛运动的初速度之比为 v1:v2=1:3 (2)第一个球落地后反弹做斜抛运动,根据运动的对称性可知,DB段和OB段是相同的平抛运动,则两球下落相同高度(H-h)后水平距离之和为 x1′+x2′=2x1 而 x1=v1t1,x1′=v1t2,x2′=v2t2 联立可得 t1=2t2 根据公式得 即 H=4(H-h) 解得 H:h=4:3 18.(1)50m/s;(2)见解析;(3)见解析 【解析】 (1)子弹射出枪口后做平抛运动,小球C做自由落体运动,两者在竖直方向的运动相同,小球C下落20m时被击中,则有 解得 这段时间内,子弹水平匀速运动了s=100m,根据 解得 (2)如果子弹离开枪口时的速度大于上面所求的数值,由于子弹和小球在竖直方向运动相同,则子弹仍可以击中小球,并且击中时间缩短。 (3)如果悬挂小球的细线突然断开后,小球C不是由静止开始下落,而是和子弹同时以10m/s的初速度沿子弹初速度方向水平抛出,则子弹和小球均做平抛运动,竖直方向上运动情况相同,水平方向上,两者都做匀速直线运动,子弹的速度大,可以击中小球。水平方向上 解得 竖直方向上 水平方向上 即在子弹射出后2.5s击中,位置在小球C的原始悬挂点右侧水平距离25m,竖直距离31.25m处。 19.(1)4.9s;(2) 【解析】 (1)平抛运动过程有 选手在水平方向上的位移 则匀加速运动的位移 解得 所以总时间 (2)设水平跃出速度为,落到传送带反应时间内向左位移大小 然后向左减速至速度为零,向左发生位移 不从传送带上掉下,平抛水平位移 所以 所以最小速度为。 20.(1);(2);(3),与斜面的夹角为 【解析】 (1)将初速度为沿竖直方向分解得 由公式得 解得竖直方向上升的最大高度为 (2)经分析,当速度方向与斜面PQ平行时离斜面距离最大,将初速度和加速度分别分解在沿斜面方向和垂直斜面方向,则沿斜面方向有 , 垂直斜面方向有 , 运动员腾空中离PQ的最大距离为H,则有 解得 (3)设运动员从O点到离PQ最远的时间为t,则有 运动员再滑入轨道时,垂直斜面方向的速度大小不变,仍为 沿斜面向下的速度为 则到达A点时的速度大小为 到达A点时的速度方向与斜面的夹角正切值为 解得
1
