2021-2022学年北师大版七年级数学上册第3章整式及其加减寒假复习自主达标测评 (word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册第3章整式及其加减寒假复习自主达标测评 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 351.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版七年级数学上册《第3章整式及其加减》
寒假复习自主达标测评(附答案)
一、单选题(满分40分)
1.下面的说法正确的是( )
A.0不是单项式 B.是同类项
C.是五次单项式 D.是二次单项式
2.下列去括号正确的是( )
A.3a-(2a-c)=3a-2a+c B.3a+2(2b-3c)=3a+4b-3c
C.6a+(-2b+6)=6a+2b-6 D.(5x-3y)-(2x-y)=5x+3y-2x+y
3.下列说法正确的是( )
A.与是同类项 B.与是同类项
C.与是同类项 D.与是同类项
4.若时,式子的值为,则当时,式子的值为( ).
A. B. C. D.
5.对于任意正整数,多项式与多项式的和一定是( )A.偶数 B.奇数 C.的倍数 D.以上都不对
6.观察以下等式:,,,,,,……那么式子的末尾数字是( )
A.0 B.2 C.3 D.9
7.已知时,代数式的值是,当时,代数式的值等于( )A. B. C. D.
8.按如图所示的规律搭正方形:搭一个小正方形需要4根小棒,搭两个小正方形需要7根小棒,搭2021个这样的小正方形需要小棒( )根.
A.8080 B.6066 C.6061 D.6064
9.观察下面三行数:
第一行数:2、-4、8、-16、32、-64、…
第二行数:0、-6、6、-18、30、-66、…
第三行数:0、-3、3、-9、15、-33、…
根据第一行数的排列规律,以及这三行数字之间的关系,确定第三行第8个数是( )
A.128 B.129 C.-128 D.-129
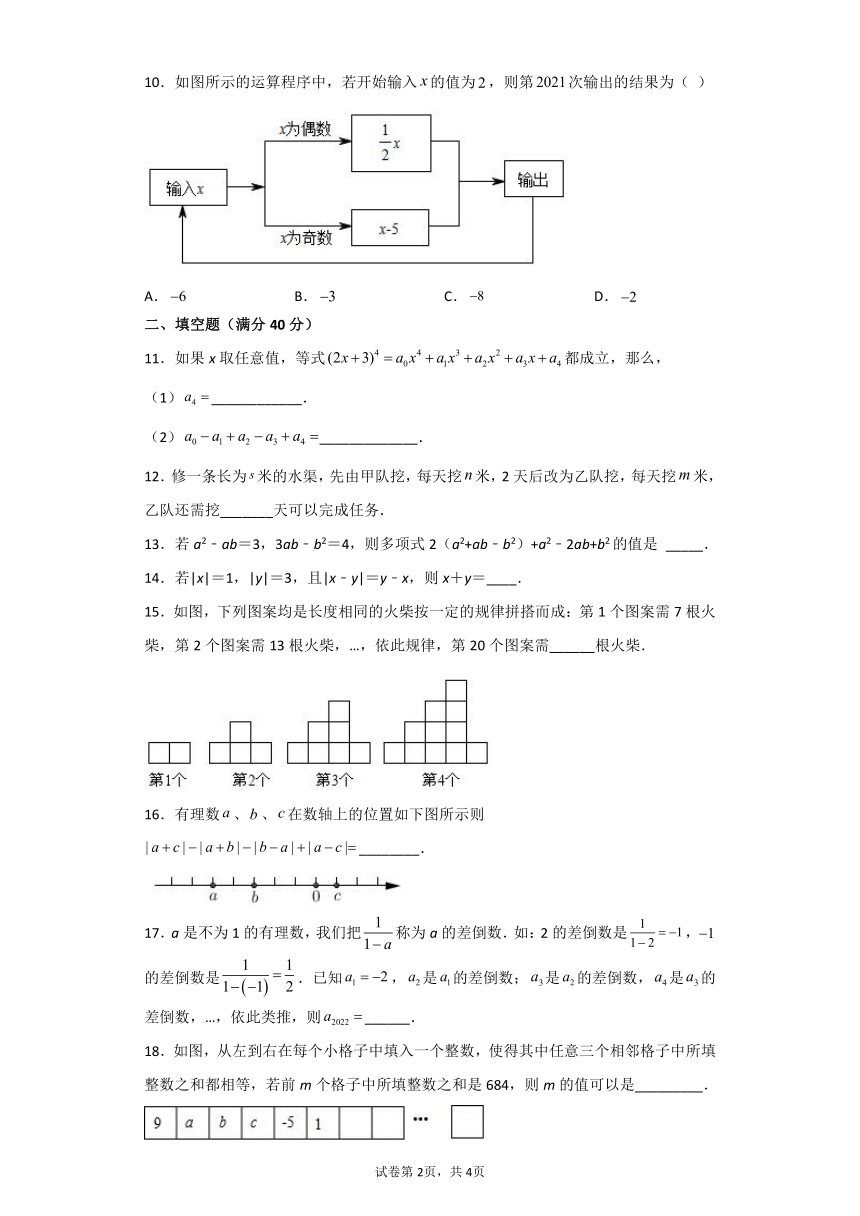
10.如图所示的运算程序中,若开始输入的值为,则第次输出的结果为( )
A. B. C. D.
二、填空题(满分40分)
11.如果x取任意值,等式都成立,那么,
(1)____________.
(2)_____________.
12.修一条长为米的水渠,先由甲队挖,每天挖米,2天后改为乙队挖,每天挖米,乙队还需挖_______天可以完成任务.
13.若a2﹣ab=3,3ab﹣b2=4,则多项式2(a2+ab﹣b2)+a2﹣2ab+b2的值是 _____.
14.若|x|=1,|y|=3,且|x﹣y|=y﹣x,则x+y=____.
15.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第20个图案需______根火柴.
16.有理数、、在数轴上的位置如下图所示则________.
17.a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是,的差倒数是.已知,是的差倒数;是的差倒数,是的差倒数,…,依此类推,则______.
18.如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,若前m个格子中所填整数之和是684,则m的值可以是_________.
19.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出b=_____.
20.将一列有理数﹣1,2,﹣3,4,﹣5,6,…,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰7”中C的位置是有理数___,﹣2021应排在A、B、C、D、E中 ___的位置.
三、解答题(满分40分)
21.先化简,再求值:
(1)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=﹣1,y=;
(2)3x2y﹣[2xy2﹣2(xy﹣x2y)﹣xy]+2xy2,其中x=﹣3,y=.
22.已知代数式A=2x2+5xy﹣7y﹣3,B=x2﹣xy+2.
(1)求3A﹣(2A+3B)的值;
(2)若A﹣2B的值与x的取值无关,求y的值;
(3)若3A﹣(2A+3B)的值与y的取值无关,求此时3A﹣(2A+3B)的值.
23.(阅读理解)
根据合并同类项法则,得4x﹣2x+x=(4﹣2+1)x=3x;类似地,如果把(a+b)看成一个整体,那么4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b);这种解决问题的思想方法被称为“整体思想”,在多项式的化简与求值中,整体思想的应用极为广泛.
(尝试应用)
(1)把(a﹣b)2看成一个整体,合并4(a﹣b)2﹣6(a﹣b)2+8(a﹣b)2的结果是 ;
(2)已知x2﹣2y=1,求2021x2﹣4042y+1的值;
(拓展探索)
(3)已知a﹣2b=2,2b﹣c=﹣5,c﹣d=9,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
24.某单位准备组织部分员工到外地参观学习,现联系了甲、乙两家旅行社,两家旅行社报价均为20元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:甲旅行社对每位员工七五折优惠(全票价收费);而乙旅行社是免去一位带队员工的费用,其余员工八折优惠(全票价收费).
(1)如果设参加旅游的员工共有人,则甲旅行社的费用为_________元,乙旅行社的费用为______元;(用含a的代数式表示,并化简)
(2)假如这个单位现组织17名员工到外地参观学习,该单位选择哪一家旅行社比较优惠?请说明理由.
(3)如果计划在10月份之内组织员工外出参观学习五天,设最中间一天的日期为a,则这五天的日期之和为______.(用含a的代数式表示)假如这五天的日期之和为30的整倍数,则他们可能于10月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程)
25.我市为提升生态环境质量,面向全市招募绿化养护公司,现甲、乙两家公司各自推出了如下收费方案.
甲公司方案:每月每平方米绿化养护费用为10元.
乙公司方案:每月收取基础养护费用400元,然后每月每平方米绿化养护费用为8元.
设每月绿化面积为x平方米:
(1)请用含x的代数式分别表示甲、乙两家公司每月的费用;
(2)如果某学校目前每月的绿化面积是600平方米,请通过计算说明选择哪家公司比较合算.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
解:A、0是单项式,故本选项错误;
B、所有常数项都是同类项,故34和43是同类项,本选项正确;
C、3a2b3c是六次单项式,故本选项错误;
D、 不是单项式,故本选项错误.
故选:B.
2.A
解:A、,故本选项正确;
B、,故本选项错误;
C、,故本选项错误;
D、,故本选项正确.
故选:A.
3.D
解:与所含字母不同,不是同类项,故A不符合题意;
与,其中不是单项式,不是同类项,故B不符合题意;
与相同字母的指数不相同,不是同类项,故C不符合题意;
与所含字母相同,相同字母的指数也相同,是同类项,故D符合题意;
故选D
4.C
解:把代入式子得:,
∴,
把代入式子得:,
∵,
∴;
故选C.
5.B
解:,
,
,
∵x是整数,7是奇数,也是奇数,
∴是奇数,
∴两个多项式的和一定是奇数;
故选:B.
6.C
解:令,
∴,
则,
∴,
∵,,,,,,,
可得出结论,每四位一个循环,
又∵,
∴的末尾数字是3;
故选C.
7.B
解:将代入代数式得
,即
将代入代数式得
故选B
8.D
解:搭2个正方形需要4+3×1=7根火柴棒;
搭3个正方形需要4+3×2=10根火柴棒;
…,
搭n个这样的正方形需要4+3(n-1)=3n+1根火柴棒;
搭2021个这样的正方形需要3×2021+1=6064根火柴棒.
故选:D.
9.D
解:根据第一行数的规律:第n个数为-(-2)n,则第一行第8个数为-256;
第二行数中每个数比第一行中对应的数小2,则第二行数的第8个数为-258;
第三行数中每个数是第二行中对应的数的一半,则第三行数的第8个数为-129;
故选:D
10.A
解:第1次输出的结果为,
第2次输出的结果为,
第3次输出的结果为,
第4次输出的结果为,
第5次输出的结果为,
第6次输出的结果为,
第7次输出的结果为,
第8次输出的结果为,
由此可知,从第2次开始,输出的结果是以循环往复的,
因为,
所以第2021次输出的结果与第5次输出的结果相同,即为,
故选:A.
11.81 1
解:(1)当时,
∴
故答案为:81
(2)取,则有
即 故答案为:1
12.
解:根据题意,剩余的任务为,乙队每天挖米,则乙队还需挖天可以完成任务.
故答案为:
13.13
解:∵a2﹣ab=3,3ab﹣b2=4,
∴原式=2a2+2ab﹣2b2+a2﹣2ab+b2
=3a2﹣b2
=3(a2﹣ab)+(3ab﹣b2)
=3×3+4
=9+4
=13.
故答案为:13.
14.2或4
解:∵,,
∴,,
∵|x﹣y|=y﹣x
∴x-y<0,即x①当x=1,y=3时,x+y=4;
②当x=-1,y=3时,x+y=2;
∴x+y=2或4.
故答案为:2或4.
15.463
解:第1个图案需7根火柴,7=1×(1+3)+3,
第2个图案需13根火柴,13=2×(2+3)+3,
第3个图案需21根火柴,21=3×(3+3)+3,
…,
则第n个图案需火柴的根数为n(n+3)+3,
故第20个图案需要的火柴的根数为:20×(20+3)+3=463,
故答案为:463.
16.0
解:根据数轴可知,
c>b>a,且c>0,0>b>a,,
∴,,,,
∴
=
=
=.
故答案为:0.
17.
解:由题意得:,
,
,
由此可知,的值是按进行循环的,
因为,
所以,
故答案为:.
18.406或410或406
解:由题意可知:9+a+b=a+b+c,
∴c=9,
又
∴b=1,
又
∴a=-5.
∵9+(-5)+1=5,
684÷5=136…4,
且5+4=9,9-5=4,
∴m=135×3+1=406或m=336×3+2=410.
故答案为:406或410.
19.91
解:分析正方形中的四个数:
∵第一个正方形中0+3=3,0+4=4,3×4+1=13;
第二个正方形中2+3=5,2+4=6,5×6+1=31;
第三个正方形中4+3=7,4+4=8,7×8+1=57.
∴c=6+3=9,a=6+4=10,b=9×10+1=91,
故答案为:91.
20.34 E
解:由图形的变化可知,每个峰需要5个数,且第奇数个峰是正数,第偶数个峰是负数,
∴“峰7”中C的位置是5×7-1=34,
∵(2021-1)÷5=404,
∴-2021是“峰404”的第5个数,应排在A、B、C、D、E中的E的位置,
故答案为:34,E.
21.(1)﹣5x2y+5xy,-5;(2)3xy,-15
解:(1)原式
,
当,时,原式;
(2)原式
,
当,,原式=.
22.(1);(2);(3)
解:(1)∵A=2x2+5xy﹣7y﹣3,B=x2﹣xy+2,
∴3A﹣(2A+3B),
=3A﹣2A﹣3B,
=A﹣3B,
=(2x2+5xy﹣7y﹣3)﹣3(x2﹣xy+2),
=2x2+5xy﹣7y﹣3﹣3x2+3xy﹣6,
=﹣x2+8xy﹣7y﹣9;
(2)∵A=2x2+5xy﹣7y﹣3,B=x2﹣xy+2,
∴A﹣2B,
=(2x2+5xy﹣7y﹣3)﹣2(x2﹣xy+2),
=2x2+5xy﹣7y﹣3﹣2x2+2xy﹣4,
=7xy﹣7y﹣7,
=7y(x﹣1)﹣7,
∵A﹣2B的值与x的取值无关,则x=1
∴y=0;
(3)∵3A﹣(2A+3B),
=﹣x2+8xy﹣7y﹣9,
=﹣x2+(8x﹣7)y﹣9,
又∵3A﹣(2A+3B)的值与y的取值无关,
∴8x﹣7=0,
∴x=,
∴3A﹣(2A+3B),
=﹣x2﹣9,
=﹣()2﹣9,
=.
23.(1);(2)2022;(3)6.
解:(1)原式,
故答案为:;
(2),
,
,
;
(3),,,
,
,
,
.
24.(1)15a,16a-16;(2)这个单位现组织17名员工到外地参观学习,该单位选择甲旅行社比较优惠;(3)他们可能是10月4号或10号或16号或22号出发
解:(1)由题意可得,
甲旅行社的费用为:20a×0.75=15a;
乙旅行社的费用为:20×(a-1)×0.8=16a-16.
故答案为:15a,16a-16;
(2)这个单位现组织17名员工到外地参观学习,该单位选择甲旅行社比较优惠,
理由:当a=17时,甲旅行社的费用为:15×17=255元;
当a=17时,乙旅行社的费用为:16a-16=16×17-16=256元,
∵255<256,
∴这个单位现组织17名员工到外地参观学习,该单位选择甲旅行社比较优惠;
(3)由题意得:这五天的日期之和为,
∵这五天的日期之和为30的整倍数,
∴(k为正整数),
当时,,符合题意;
当时,,符合题意;
当时,,符合题意;
当时,,符合题意;
当时,(因为一个月不会有32天),不符合题意;
∴他们可能是10月4号或10号或16号或22号出发.
25.(1)甲公司元;乙公司元;(2)乙公司更合算
解:(1)根据题意:
甲公司每月的费用:元,
乙公司每月的费用:元;
(2)根据题意平方米时,
甲公司每月的费用:元,
乙公司每月的费用:元,
,
∴乙公司更合算.
寒假复习自主达标测评(附答案)
一、单选题(满分40分)
1.下面的说法正确的是( )
A.0不是单项式 B.是同类项
C.是五次单项式 D.是二次单项式
2.下列去括号正确的是( )
A.3a-(2a-c)=3a-2a+c B.3a+2(2b-3c)=3a+4b-3c
C.6a+(-2b+6)=6a+2b-6 D.(5x-3y)-(2x-y)=5x+3y-2x+y
3.下列说法正确的是( )
A.与是同类项 B.与是同类项
C.与是同类项 D.与是同类项
4.若时,式子的值为,则当时,式子的值为( ).
A. B. C. D.
5.对于任意正整数,多项式与多项式的和一定是( )A.偶数 B.奇数 C.的倍数 D.以上都不对
6.观察以下等式:,,,,,,……那么式子的末尾数字是( )
A.0 B.2 C.3 D.9
7.已知时,代数式的值是,当时,代数式的值等于( )A. B. C. D.
8.按如图所示的规律搭正方形:搭一个小正方形需要4根小棒,搭两个小正方形需要7根小棒,搭2021个这样的小正方形需要小棒( )根.
A.8080 B.6066 C.6061 D.6064
9.观察下面三行数:
第一行数:2、-4、8、-16、32、-64、…
第二行数:0、-6、6、-18、30、-66、…
第三行数:0、-3、3、-9、15、-33、…
根据第一行数的排列规律,以及这三行数字之间的关系,确定第三行第8个数是( )
A.128 B.129 C.-128 D.-129
10.如图所示的运算程序中,若开始输入的值为,则第次输出的结果为( )
A. B. C. D.
二、填空题(满分40分)
11.如果x取任意值,等式都成立,那么,
(1)____________.
(2)_____________.
12.修一条长为米的水渠,先由甲队挖,每天挖米,2天后改为乙队挖,每天挖米,乙队还需挖_______天可以完成任务.
13.若a2﹣ab=3,3ab﹣b2=4,则多项式2(a2+ab﹣b2)+a2﹣2ab+b2的值是 _____.
14.若|x|=1,|y|=3,且|x﹣y|=y﹣x,则x+y=____.
15.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第20个图案需______根火柴.
16.有理数、、在数轴上的位置如下图所示则________.
17.a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是,的差倒数是.已知,是的差倒数;是的差倒数,是的差倒数,…,依此类推,则______.
18.如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,若前m个格子中所填整数之和是684,则m的值可以是_________.
19.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出b=_____.
20.将一列有理数﹣1,2,﹣3,4,﹣5,6,…,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰7”中C的位置是有理数___,﹣2021应排在A、B、C、D、E中 ___的位置.
三、解答题(满分40分)
21.先化简,再求值:
(1)2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=﹣1,y=;
(2)3x2y﹣[2xy2﹣2(xy﹣x2y)﹣xy]+2xy2,其中x=﹣3,y=.
22.已知代数式A=2x2+5xy﹣7y﹣3,B=x2﹣xy+2.
(1)求3A﹣(2A+3B)的值;
(2)若A﹣2B的值与x的取值无关,求y的值;
(3)若3A﹣(2A+3B)的值与y的取值无关,求此时3A﹣(2A+3B)的值.
23.(阅读理解)
根据合并同类项法则,得4x﹣2x+x=(4﹣2+1)x=3x;类似地,如果把(a+b)看成一个整体,那么4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b);这种解决问题的思想方法被称为“整体思想”,在多项式的化简与求值中,整体思想的应用极为广泛.
(尝试应用)
(1)把(a﹣b)2看成一个整体,合并4(a﹣b)2﹣6(a﹣b)2+8(a﹣b)2的结果是 ;
(2)已知x2﹣2y=1,求2021x2﹣4042y+1的值;
(拓展探索)
(3)已知a﹣2b=2,2b﹣c=﹣5,c﹣d=9,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
24.某单位准备组织部分员工到外地参观学习,现联系了甲、乙两家旅行社,两家旅行社报价均为20元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:甲旅行社对每位员工七五折优惠(全票价收费);而乙旅行社是免去一位带队员工的费用,其余员工八折优惠(全票价收费).
(1)如果设参加旅游的员工共有人,则甲旅行社的费用为_________元,乙旅行社的费用为______元;(用含a的代数式表示,并化简)
(2)假如这个单位现组织17名员工到外地参观学习,该单位选择哪一家旅行社比较优惠?请说明理由.
(3)如果计划在10月份之内组织员工外出参观学习五天,设最中间一天的日期为a,则这五天的日期之和为______.(用含a的代数式表示)假如这五天的日期之和为30的整倍数,则他们可能于10月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程)
25.我市为提升生态环境质量,面向全市招募绿化养护公司,现甲、乙两家公司各自推出了如下收费方案.
甲公司方案:每月每平方米绿化养护费用为10元.
乙公司方案:每月收取基础养护费用400元,然后每月每平方米绿化养护费用为8元.
设每月绿化面积为x平方米:
(1)请用含x的代数式分别表示甲、乙两家公司每月的费用;
(2)如果某学校目前每月的绿化面积是600平方米,请通过计算说明选择哪家公司比较合算.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
解:A、0是单项式,故本选项错误;
B、所有常数项都是同类项,故34和43是同类项,本选项正确;
C、3a2b3c是六次单项式,故本选项错误;
D、 不是单项式,故本选项错误.
故选:B.
2.A
解:A、,故本选项正确;
B、,故本选项错误;
C、,故本选项错误;
D、,故本选项正确.
故选:A.
3.D
解:与所含字母不同,不是同类项,故A不符合题意;
与,其中不是单项式,不是同类项,故B不符合题意;
与相同字母的指数不相同,不是同类项,故C不符合题意;
与所含字母相同,相同字母的指数也相同,是同类项,故D符合题意;
故选D
4.C
解:把代入式子得:,
∴,
把代入式子得:,
∵,
∴;
故选C.
5.B
解:,
,
,
∵x是整数,7是奇数,也是奇数,
∴是奇数,
∴两个多项式的和一定是奇数;
故选:B.
6.C
解:令,
∴,
则,
∴,
∵,,,,,,,
可得出结论,每四位一个循环,
又∵,
∴的末尾数字是3;
故选C.
7.B
解:将代入代数式得
,即
将代入代数式得
故选B
8.D
解:搭2个正方形需要4+3×1=7根火柴棒;
搭3个正方形需要4+3×2=10根火柴棒;
…,
搭n个这样的正方形需要4+3(n-1)=3n+1根火柴棒;
搭2021个这样的正方形需要3×2021+1=6064根火柴棒.
故选:D.
9.D
解:根据第一行数的规律:第n个数为-(-2)n,则第一行第8个数为-256;
第二行数中每个数比第一行中对应的数小2,则第二行数的第8个数为-258;
第三行数中每个数是第二行中对应的数的一半,则第三行数的第8个数为-129;
故选:D
10.A
解:第1次输出的结果为,
第2次输出的结果为,
第3次输出的结果为,
第4次输出的结果为,
第5次输出的结果为,
第6次输出的结果为,
第7次输出的结果为,
第8次输出的结果为,
由此可知,从第2次开始,输出的结果是以循环往复的,
因为,
所以第2021次输出的结果与第5次输出的结果相同,即为,
故选:A.
11.81 1
解:(1)当时,
∴
故答案为:81
(2)取,则有
即 故答案为:1
12.
解:根据题意,剩余的任务为,乙队每天挖米,则乙队还需挖天可以完成任务.
故答案为:
13.13
解:∵a2﹣ab=3,3ab﹣b2=4,
∴原式=2a2+2ab﹣2b2+a2﹣2ab+b2
=3a2﹣b2
=3(a2﹣ab)+(3ab﹣b2)
=3×3+4
=9+4
=13.
故答案为:13.
14.2或4
解:∵,,
∴,,
∵|x﹣y|=y﹣x
∴x-y<0,即x
②当x=-1,y=3时,x+y=2;
∴x+y=2或4.
故答案为:2或4.
15.463
解:第1个图案需7根火柴,7=1×(1+3)+3,
第2个图案需13根火柴,13=2×(2+3)+3,
第3个图案需21根火柴,21=3×(3+3)+3,
…,
则第n个图案需火柴的根数为n(n+3)+3,
故第20个图案需要的火柴的根数为:20×(20+3)+3=463,
故答案为:463.
16.0
解:根据数轴可知,
c>b>a,且c>0,0>b>a,,
∴,,,,
∴
=
=
=.
故答案为:0.
17.
解:由题意得:,
,
,
由此可知,的值是按进行循环的,
因为,
所以,
故答案为:.
18.406或410或406
解:由题意可知:9+a+b=a+b+c,
∴c=9,
又
∴b=1,
又
∴a=-5.
∵9+(-5)+1=5,
684÷5=136…4,
且5+4=9,9-5=4,
∴m=135×3+1=406或m=336×3+2=410.
故答案为:406或410.
19.91
解:分析正方形中的四个数:
∵第一个正方形中0+3=3,0+4=4,3×4+1=13;
第二个正方形中2+3=5,2+4=6,5×6+1=31;
第三个正方形中4+3=7,4+4=8,7×8+1=57.
∴c=6+3=9,a=6+4=10,b=9×10+1=91,
故答案为:91.
20.34 E
解:由图形的变化可知,每个峰需要5个数,且第奇数个峰是正数,第偶数个峰是负数,
∴“峰7”中C的位置是5×7-1=34,
∵(2021-1)÷5=404,
∴-2021是“峰404”的第5个数,应排在A、B、C、D、E中的E的位置,
故答案为:34,E.
21.(1)﹣5x2y+5xy,-5;(2)3xy,-15
解:(1)原式
,
当,时,原式;
(2)原式
,
当,,原式=.
22.(1);(2);(3)
解:(1)∵A=2x2+5xy﹣7y﹣3,B=x2﹣xy+2,
∴3A﹣(2A+3B),
=3A﹣2A﹣3B,
=A﹣3B,
=(2x2+5xy﹣7y﹣3)﹣3(x2﹣xy+2),
=2x2+5xy﹣7y﹣3﹣3x2+3xy﹣6,
=﹣x2+8xy﹣7y﹣9;
(2)∵A=2x2+5xy﹣7y﹣3,B=x2﹣xy+2,
∴A﹣2B,
=(2x2+5xy﹣7y﹣3)﹣2(x2﹣xy+2),
=2x2+5xy﹣7y﹣3﹣2x2+2xy﹣4,
=7xy﹣7y﹣7,
=7y(x﹣1)﹣7,
∵A﹣2B的值与x的取值无关,则x=1
∴y=0;
(3)∵3A﹣(2A+3B),
=﹣x2+8xy﹣7y﹣9,
=﹣x2+(8x﹣7)y﹣9,
又∵3A﹣(2A+3B)的值与y的取值无关,
∴8x﹣7=0,
∴x=,
∴3A﹣(2A+3B),
=﹣x2﹣9,
=﹣()2﹣9,
=.
23.(1);(2)2022;(3)6.
解:(1)原式,
故答案为:;
(2),
,
,
;
(3),,,
,
,
,
.
24.(1)15a,16a-16;(2)这个单位现组织17名员工到外地参观学习,该单位选择甲旅行社比较优惠;(3)他们可能是10月4号或10号或16号或22号出发
解:(1)由题意可得,
甲旅行社的费用为:20a×0.75=15a;
乙旅行社的费用为:20×(a-1)×0.8=16a-16.
故答案为:15a,16a-16;
(2)这个单位现组织17名员工到外地参观学习,该单位选择甲旅行社比较优惠,
理由:当a=17时,甲旅行社的费用为:15×17=255元;
当a=17时,乙旅行社的费用为:16a-16=16×17-16=256元,
∵255<256,
∴这个单位现组织17名员工到外地参观学习,该单位选择甲旅行社比较优惠;
(3)由题意得:这五天的日期之和为,
∵这五天的日期之和为30的整倍数,
∴(k为正整数),
当时,,符合题意;
当时,,符合题意;
当时,,符合题意;
当时,,符合题意;
当时,(因为一个月不会有32天),不符合题意;
∴他们可能是10月4号或10号或16号或22号出发.
25.(1)甲公司元;乙公司元;(2)乙公司更合算
解:(1)根据题意:
甲公司每月的费用:元,
乙公司每月的费用:元;
(2)根据题意平方米时,
甲公司每月的费用:元,
乙公司每月的费用:元,
,
∴乙公司更合算.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
