2022年中考二轮复习《二次函数的应用》专题复习导学案(含答案)
文档属性
| 名称 | 2022年中考二轮复习《二次函数的应用》专题复习导学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 197.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 00:00:00 | ||
图片预览



文档简介
二次函数的应用
【教学前测】
1.某商场降价销售一批名牌球鞋,已知所获利润y(元)与降价金额x(元)之间满定函数关系式y=﹣x2+50x+600,若降价10元,则获利为( )
A.800元 B.600元 C.1200元 D.1000元
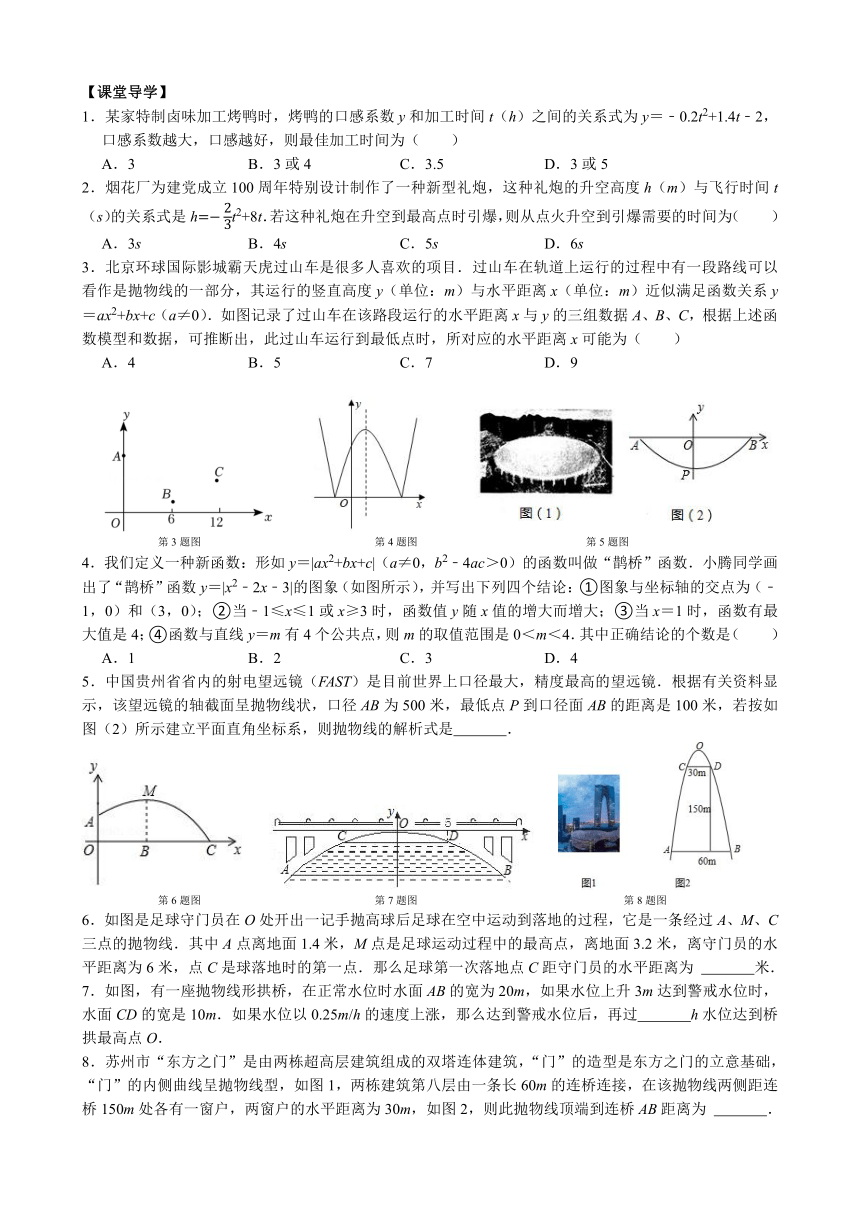
2.从底面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:h=30t﹣5t2,这个函数图象如图所示,则小球从第3s到第5s的下降的高度为( )
A.15m B.20m C.25m D.30m
3.汽车在刹车后,由于惯性作用还要继续向前滑行一段距离才能停下,我们称这段距离为“刹车距离”,刹车距离往往跟行驶速度有关,在一个限速35km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不妙,同时刹车,最后还是相撞了事发后,交警现场测得甲车的刹车距离略超过12m,乙车的刹车距离略超过10m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)的关系大致如下:S甲x,S乙.由此可以推测( )
A.甲车超速 B.乙车超速 C.两车都超速 D.两车都未超速
4.把一个物体从地面以10m/s速度竖直上抛,那么物体经过x(s)时,离地面高度为h(m),h与x的函数关系为h=10x﹣4.9x2,则物体回到地面的时间为 s.
5.如图,在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB,CD,以点B为坐标原点,直线BD为x轴建立平面直角坐标系.已知电线杆之间的电线可近似地看成抛物线y=0.8x2﹣3.2x+6,则电线最低点离地面的距离是 米.
6.用长为120米的篱笆围一个矩形苗圃,则能围成苗圃的最大面积是 .
7.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为12m.现将它的图形放在如图所示的直角坐标系中.
(1)求这条抛物线的解析式.
(2)一艘宽为4米,高出水面3米的货船,能否从桥下通过?
【课堂导学】
1.某家特制卤味加工烤鸭时,烤鸭的口感系数y和加工时间t(h)之间的关系式为y=﹣0.2t2+1.4t﹣2,口感系数越大,口感越好,则最佳加工时间为( )
A.3 B.3或4 C.3.5 D.3或5
2.烟花厂为建党成立100周年特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是ht2+8t.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
3.北京环球国际影城霸天虎过山车是很多人喜欢的项目.过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,其运行的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了过山车在该路段运行的水平距离x与y的三组数据A、B、C,根据上述函数模型和数据,可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
A.4 B.5 C.7 D.9
第3题图 第4题图 第5题图
4.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小腾同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列四个结论:①图象与坐标轴的交点为(﹣1,0)和(3,0);②当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;③当x=1时,函数有最大值是4;④函数与直线y=m有4个公共点,则m的取值范围是0<m<4.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5.中国贵州省省内的射电望远镜(FAST)是目前世界上口径最大,精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点P到口径面AB的距离是100米,若按如图(2)所示建立平面直角坐标系,则抛物线的解析式是 .
第6题图 第7题图 第8题图
6.如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程,它是一条经过A、M、C三点的抛物线.其中A点离地面1.4米,M点是足球运动过程中的最高点,离地面3.2米,离守门员的水平距离为6米,点C是球落地时的第一点.那么足球第一次落地点C距守门员的水平距离为 米.
7.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m达到警戒水位时,水面CD的宽是10m.如果水位以0.25m/h的速度上涨,那么达到警戒水位后,再过 h水位达到桥拱最高点O.
8.苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长60m的连桥连接,在该抛物线两侧距连桥150m处各有一窗户,两窗户的水平距离为30m,如图2,则此抛物线顶端到连桥AB距离为 .
9.如图,根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.我校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长4.5米),其它三面用防疫隔离材料搭建,与墙垂直的一边还要开一扇1米宽的进出口(不需材料),共用防疫隔离材料8米.
(1)若面积为10平方米,隔离区的长和宽分别是多少米?
(2)隔离区的面积有最大值吗?最大为多少平方米?
10.“双减”政策落地后,对校外培训机构的影响巨大,不管是机构还是机构老师都面临着转型,培训机构李老师推出了“热学文化”新零售项目.他新开了甲、乙两家分店共同销售,因地段不同,甲店一天可售出某品牌科技产品20件,每件盈利26元;乙店一天可售出同一品牌科技产品32件,每件盈利20元.经调查发现,每件此种科技产品每降价1元,甲、乙两家店一天都可多售出2件.设甲店每件降价a元时,一天可盈利y1元,乙店每件降价b元时,一天可盈利y2元.
(1)当a=5时,求y1的值.
(2)求y2关于b的函数表达式.
(3)若李老师规定两家分店下降的价格必须相同,请求出每件此种科技产品下降多少元时,两家分店一天的盈利和最大,最大是多少元?
【教学后测】
1.某旅行社组团去旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即参团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是( )
A.56 B.55 C.54 D.53
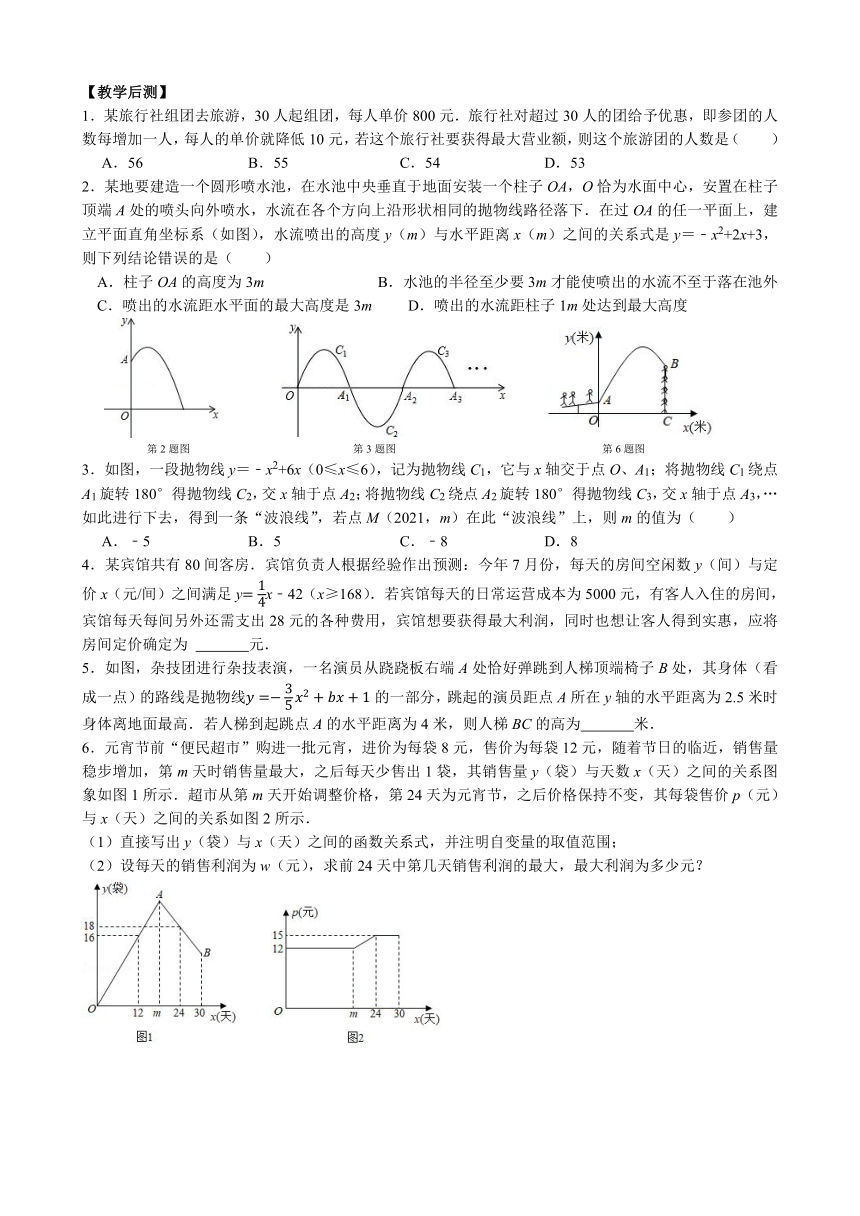
2.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+3,则下列结论错误的是( )
A.柱子OA的高度为3m B.水池的半径至少要3m才能使喷出的水流不至于落在池外
C.喷出的水流距水平面的最大高度是3m D.喷出的水流距柱子1m处达到最大高度
第2题图 第3题图 第6题图
3.如图,一段抛物线y=﹣x2+6x(0≤x≤6),记为抛物线C1,它与x轴交于点O、A1;将抛物线C1绕点A1旋转180°得抛物线C2,交x轴于点A2;将抛物线C2绕点A2旋转180°得抛物线C3,交x轴于点A3,…如此进行下去,得到一条“波浪线”,若点M(2021,m)在此“波浪线”上,则m的值为( )
A.﹣5 B.5 C.﹣8 D.8
4.某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足yx﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为 元.
5.如图,杂技团进行杂技表演,一名演员从跷跷板右端A处恰好弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为 米.
6.元宵节前“便民超市”购进一批元宵,进价为每袋8元,售价为每袋12元,随着节日的临近,销售量稳步增加,第m天时销售量最大,之后每天少售出1袋,其销售量y(袋)与天数x(天)之间的关系图象如图1所示.超市从第m天开始调整价格,第24天为元宵节,之后价格保持不变,其每袋售价p(元)与x(天)之间的关系如图2所示.
(1)直接写出y(袋)与x(天)之间的函数关系式,并注明自变量的取值范围;
(2)设每天的销售利润为w(元),求前24天中第几天销售利润的最大,最大利润为多少元?
参考答案与试题解析
【教学前测】
1.解:当x=10时,y=﹣102+50×10+600=1000,
故选:D.
2.解:由题意得,第3s时小球达到最高点,此时小球距离地面45m,
然后小球开始竖直下落,
当t=5s时,h=30×5﹣5×52=150﹣125=25(m),
∴从第3s到第5s下降的高度为45﹣25=20(m),
故选:B.
3.解∵甲车的刹车距离为12m,
∴x2+x=12,
即x2+10x﹣1200=0,
解得:x1=30 x2=﹣40(不合题意舍去),
所以甲车的速度为30km/h,不超过限速,
而乙车的刹车距离为10m,
则有x2+x=10,
即x2+10x﹣2000=0,
解得:x1=40,x2=﹣50(不合题意舍去),
所以乙车的速度为40km/h,超过了限速35km/h的规定.
故选:B.
4.解:(1)由图象可知,
抛物线的顶点坐标为(6,4),过点(12,0),
设抛物线的解析式为:y=a(x﹣6)2+4,
则0=a(12﹣6)2+4,
解得,a=﹣,
即这条抛物线的解析式为:y=﹣(x﹣6)2+4;
(2)当x=(12﹣4)=4时,y=﹣(4﹣6)2+4=>3,
∴货船能顺利通过此桥洞.
5.解:回到地面则h=0,即10x﹣4.9x2=0,
解得:x1=0,x2=,
∴球从弹起至回到地面需s,
故答案为:.
6.解:y=0.8x2﹣3.2x+6=0.8(x﹣2)2+2.8,
∴顶点坐标为(2,2.8),
∴电线最低点离地面的距离是2.8米,
故答案为:2.8.
7.解:设矩形苗圃的长为x米,则宽为(60﹣x)米,矩形的面积为S平方米,
由题意,得S=x(60﹣x)=﹣x2+60x=﹣(x﹣30)2+900,
∵﹣1<0,
∴当x=30时,S最大,最大值为900,
故答案为:900平方米.
【课堂导学】
1.解:∵y=﹣0.2t2+1.4t﹣2=﹣0.2(t﹣3.5)2+4.5,
∴当t=3.5时,y最大=4.5,
则最佳加工时间为3.5h,
故选:C.
2.解:∵礼炮在点火升空到最高点引爆,
∴t=﹣=﹣=6,
∴从点火升空到引爆需要的时间为6s,
故选:D.
3.解:设该抛物线的对称轴为x,
由图象可得,
解得6<x<9,
故选:C.
4.解:①∵(﹣1,0),(3,0)和(0,3)坐标都满足函数y=|x2﹣2x﹣3|,
∴①是错误的;
②根据函数的图象和性质,发现当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大,因此②是正确的;
③由图象可知,当x<﹣1时,函数值随x的减小而增大,当x>3时,函数值随x的增大而增大,均存在大于顶点坐标的函数值,故当x=1时的函数值4并非最大值,故③错误.
④由图象可知,函数与直线y=m有4个公共点,则m的取值范围是0<m<4,故④正确.
故选:B.
5.解:由题意可得:A(﹣250,0),P(0,﹣100),
设抛物线解析式为:y=ax2﹣100,
则0=62500a﹣100,
解得:a=,
故抛物线解析式为:y=x2﹣100.
故答案为:y=x2﹣100.
6.解:设抛物线的解析式为y=a(x﹣6)2+3.2,
将点A(0,1.4)代入,得:36a+3.2=1.4,
解得:a=﹣0.05,
则抛物线的解析式为y=﹣0.05(x﹣6)2+3.2;
当y=0时,﹣0.05(x﹣6)2+3.2=0,
解得:x1=﹣2(舍),x2=14,
所以足球第一次落地点C距守门员14米.
故答案为:14.
7.解:设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
由题意:,
解得,
∴y=﹣x2,
当x=5时,y=﹣1,
故t==4(h),
答:再过4小时水位达到桥拱最高点O.
故答案为:4.
8.解:以AB所在的直线为x轴,以线段AB的垂直平分线所在的直线为y轴建立平面直角坐标系:
∴A(﹣30,0),B(30,0),D(15,150),
设抛物线的解析式为y=a(x+30)(x﹣30),将(15,150)代入,得:
150=a(15+30)(15﹣30),
解得:a=﹣,
∴y=﹣(x+30)(x﹣30)
=﹣x2+200,
∴抛物线顶端O的坐标为(0,200),
∴此抛物线顶端O到连桥AB距离为200m.
故答案为:200m.
9.解:(1)设这个隔离区一边AB长为x米,则另一边BC长为(8﹣x+1)米.
依题意,得x (8﹣x+1)=10,
解得x1=5,x2=4.
当x=5时,5>4.5(舍去),
当x=4时,(8﹣x+1)=2.5(米)<4.5米.
∴若面积为10平方米,隔离区的长为4米,宽为2.5米.
(2)隔离区有最大面积,理由如下:
由(1)知,隔离区的面积为x (8﹣x+1)=﹣x2+x=﹣(x﹣)2+,
∵﹣<0,
∴当x=时,隔离区有最大面积,最大面积为平方米.
10.解:(1)由题意可得,
y1=(26﹣a)(20+2a),
当a=5时,y1=(26﹣5)×(20+2×5)=630,
即当a=5时,y1的值是630;
(2)由题意可得,
y2=(20﹣b)(32+2b)=﹣2b2+8b+640,
即y2关于b的函数表达式为y2=﹣2b2+8b+640;
(3)设两家下降的价格都为x元,两家的盈利和为w元,
w=(26﹣x)(20+2x)+(﹣2x2+8x+640)=﹣4x2+40x+1160=﹣4(x﹣5)2+1260,
∴当x=5时,w取得最大值,此时w=1260,
答:每件科技产品下降5元时,两家分店一天的盈利和最大,最大是1260元.
【教学后测】
1.解:设一个旅行团的人数是x人,设营业额为y元,根据题意可得:
y=x[800﹣10(x﹣30)]
=﹣10x2+1100x
=﹣10(x2﹣110x)
=﹣10(x﹣55)2+30250,
故当一个旅行团的人数是55人时,这个旅行社可以获得最大的营业额.
故选:B.
2.解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴当x=0时,y=3,即OA=3m,故A选项正确,
当x=1时,y取得最大值,此时y=4,故B选项正确,C选项错误,
当y=0时,x=3或x=﹣1(舍去),故D选项正确,
故选:C.
3.解:∵y=﹣x2+6x=﹣x(x﹣6)(0≤x≤6),
∴A1(6,0),
∴整个函数图象每隔6×2=12个单位长度,函数值就相等,
∵18=12×1+6,
所以m的值等于x=6时的纵坐标,
所以m=﹣6×(6﹣6)=0.
故选:D.
4.解:设每天的利润为W元,根据题意,得:
W=(x﹣28)(80﹣y)﹣5000
=(x﹣28)[80﹣(x﹣42)]﹣5000
=﹣x2+129x﹣8416
=﹣(x﹣258)2+8225,
∵当x=258时,y=×258﹣42=22.5,不是整数,
∴当x=256或x=260时,函数取得最大值,最大值为8224元,
又∵想让客人得到实惠,
∴x=260(舍去)
∴宾馆应将房间定价确定为256元时,才能获得最大利润,
故答案为:256.
5.解:∵跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.
∴抛物线的对称轴为x=2.5,
∴x=﹣=2.5,解得:b=3,
∴抛物线为y=﹣x2+3x+1,
∵人梯到起跳点A的水平距离是4,
∴点B的横坐标为4,
则yB=﹣×42+3×4+1=3.4,即BC=3.4米.
故答案为:3.4.
6.解:(1)设线段OA的关系式为y=kx,
则12k=16,
解得k=,
所以y=x.
设线段AB的关系式为y=kx+b,
则,
解得k=﹣1,b=42,
所以y=﹣x+42;
当x=﹣x+42,
解得x=18,
所以m=18,
综上,y=;
(2)当18<x≤24时,
设p=kx+b,则,
解得k=0.5,b=3,
∴p=0.5x+3;
当0≤x≤18时,
,
∵,
∴w随x增大而增大,
∴当x=18时,w最大=96;
当18<x≤24时,
w=(0.5x+3﹣8)(﹣x+42)=﹣0.5x2+26x﹣210=﹣0.5(x﹣26)2+128,
∵a=﹣0.5<0,开口向下,
∴当x<26时,w随x的增大而增大,
∴当x=24时,w最大=126,
答:第24天时销售利润最大,最大为126元.
【教学前测】
1.某商场降价销售一批名牌球鞋,已知所获利润y(元)与降价金额x(元)之间满定函数关系式y=﹣x2+50x+600,若降价10元,则获利为( )
A.800元 B.600元 C.1200元 D.1000元
2.从底面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:h=30t﹣5t2,这个函数图象如图所示,则小球从第3s到第5s的下降的高度为( )
A.15m B.20m C.25m D.30m
3.汽车在刹车后,由于惯性作用还要继续向前滑行一段距离才能停下,我们称这段距离为“刹车距离”,刹车距离往往跟行驶速度有关,在一个限速35km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不妙,同时刹车,最后还是相撞了事发后,交警现场测得甲车的刹车距离略超过12m,乙车的刹车距离略超过10m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)的关系大致如下:S甲x,S乙.由此可以推测( )
A.甲车超速 B.乙车超速 C.两车都超速 D.两车都未超速
4.把一个物体从地面以10m/s速度竖直上抛,那么物体经过x(s)时,离地面高度为h(m),h与x的函数关系为h=10x﹣4.9x2,则物体回到地面的时间为 s.
5.如图,在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB,CD,以点B为坐标原点,直线BD为x轴建立平面直角坐标系.已知电线杆之间的电线可近似地看成抛物线y=0.8x2﹣3.2x+6,则电线最低点离地面的距离是 米.
6.用长为120米的篱笆围一个矩形苗圃,则能围成苗圃的最大面积是 .
7.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为12m.现将它的图形放在如图所示的直角坐标系中.
(1)求这条抛物线的解析式.
(2)一艘宽为4米,高出水面3米的货船,能否从桥下通过?
【课堂导学】
1.某家特制卤味加工烤鸭时,烤鸭的口感系数y和加工时间t(h)之间的关系式为y=﹣0.2t2+1.4t﹣2,口感系数越大,口感越好,则最佳加工时间为( )
A.3 B.3或4 C.3.5 D.3或5
2.烟花厂为建党成立100周年特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是ht2+8t.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
3.北京环球国际影城霸天虎过山车是很多人喜欢的项目.过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,其运行的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了过山车在该路段运行的水平距离x与y的三组数据A、B、C,根据上述函数模型和数据,可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
A.4 B.5 C.7 D.9
第3题图 第4题图 第5题图
4.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小腾同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列四个结论:①图象与坐标轴的交点为(﹣1,0)和(3,0);②当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;③当x=1时,函数有最大值是4;④函数与直线y=m有4个公共点,则m的取值范围是0<m<4.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5.中国贵州省省内的射电望远镜(FAST)是目前世界上口径最大,精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点P到口径面AB的距离是100米,若按如图(2)所示建立平面直角坐标系,则抛物线的解析式是 .
第6题图 第7题图 第8题图
6.如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程,它是一条经过A、M、C三点的抛物线.其中A点离地面1.4米,M点是足球运动过程中的最高点,离地面3.2米,离守门员的水平距离为6米,点C是球落地时的第一点.那么足球第一次落地点C距守门员的水平距离为 米.
7.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m达到警戒水位时,水面CD的宽是10m.如果水位以0.25m/h的速度上涨,那么达到警戒水位后,再过 h水位达到桥拱最高点O.
8.苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长60m的连桥连接,在该抛物线两侧距连桥150m处各有一窗户,两窗户的水平距离为30m,如图2,则此抛物线顶端到连桥AB距离为 .
9.如图,根据防疫的相关要求,学生入校需晨检,体温超标的同学须进入临时隔离区进行留观.我校要建一个长方形临时隔离区,隔离区的一面利用学校边墙(墙长4.5米),其它三面用防疫隔离材料搭建,与墙垂直的一边还要开一扇1米宽的进出口(不需材料),共用防疫隔离材料8米.
(1)若面积为10平方米,隔离区的长和宽分别是多少米?
(2)隔离区的面积有最大值吗?最大为多少平方米?
10.“双减”政策落地后,对校外培训机构的影响巨大,不管是机构还是机构老师都面临着转型,培训机构李老师推出了“热学文化”新零售项目.他新开了甲、乙两家分店共同销售,因地段不同,甲店一天可售出某品牌科技产品20件,每件盈利26元;乙店一天可售出同一品牌科技产品32件,每件盈利20元.经调查发现,每件此种科技产品每降价1元,甲、乙两家店一天都可多售出2件.设甲店每件降价a元时,一天可盈利y1元,乙店每件降价b元时,一天可盈利y2元.
(1)当a=5时,求y1的值.
(2)求y2关于b的函数表达式.
(3)若李老师规定两家分店下降的价格必须相同,请求出每件此种科技产品下降多少元时,两家分店一天的盈利和最大,最大是多少元?
【教学后测】
1.某旅行社组团去旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即参团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是( )
A.56 B.55 C.54 D.53
2.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+3,则下列结论错误的是( )
A.柱子OA的高度为3m B.水池的半径至少要3m才能使喷出的水流不至于落在池外
C.喷出的水流距水平面的最大高度是3m D.喷出的水流距柱子1m处达到最大高度
第2题图 第3题图 第6题图
3.如图,一段抛物线y=﹣x2+6x(0≤x≤6),记为抛物线C1,它与x轴交于点O、A1;将抛物线C1绕点A1旋转180°得抛物线C2,交x轴于点A2;将抛物线C2绕点A2旋转180°得抛物线C3,交x轴于点A3,…如此进行下去,得到一条“波浪线”,若点M(2021,m)在此“波浪线”上,则m的值为( )
A.﹣5 B.5 C.﹣8 D.8
4.某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足yx﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为 元.
5.如图,杂技团进行杂技表演,一名演员从跷跷板右端A处恰好弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为 米.
6.元宵节前“便民超市”购进一批元宵,进价为每袋8元,售价为每袋12元,随着节日的临近,销售量稳步增加,第m天时销售量最大,之后每天少售出1袋,其销售量y(袋)与天数x(天)之间的关系图象如图1所示.超市从第m天开始调整价格,第24天为元宵节,之后价格保持不变,其每袋售价p(元)与x(天)之间的关系如图2所示.
(1)直接写出y(袋)与x(天)之间的函数关系式,并注明自变量的取值范围;
(2)设每天的销售利润为w(元),求前24天中第几天销售利润的最大,最大利润为多少元?
参考答案与试题解析
【教学前测】
1.解:当x=10时,y=﹣102+50×10+600=1000,
故选:D.
2.解:由题意得,第3s时小球达到最高点,此时小球距离地面45m,
然后小球开始竖直下落,
当t=5s时,h=30×5﹣5×52=150﹣125=25(m),
∴从第3s到第5s下降的高度为45﹣25=20(m),
故选:B.
3.解∵甲车的刹车距离为12m,
∴x2+x=12,
即x2+10x﹣1200=0,
解得:x1=30 x2=﹣40(不合题意舍去),
所以甲车的速度为30km/h,不超过限速,
而乙车的刹车距离为10m,
则有x2+x=10,
即x2+10x﹣2000=0,
解得:x1=40,x2=﹣50(不合题意舍去),
所以乙车的速度为40km/h,超过了限速35km/h的规定.
故选:B.
4.解:(1)由图象可知,
抛物线的顶点坐标为(6,4),过点(12,0),
设抛物线的解析式为:y=a(x﹣6)2+4,
则0=a(12﹣6)2+4,
解得,a=﹣,
即这条抛物线的解析式为:y=﹣(x﹣6)2+4;
(2)当x=(12﹣4)=4时,y=﹣(4﹣6)2+4=>3,
∴货船能顺利通过此桥洞.
5.解:回到地面则h=0,即10x﹣4.9x2=0,
解得:x1=0,x2=,
∴球从弹起至回到地面需s,
故答案为:.
6.解:y=0.8x2﹣3.2x+6=0.8(x﹣2)2+2.8,
∴顶点坐标为(2,2.8),
∴电线最低点离地面的距离是2.8米,
故答案为:2.8.
7.解:设矩形苗圃的长为x米,则宽为(60﹣x)米,矩形的面积为S平方米,
由题意,得S=x(60﹣x)=﹣x2+60x=﹣(x﹣30)2+900,
∵﹣1<0,
∴当x=30时,S最大,最大值为900,
故答案为:900平方米.
【课堂导学】
1.解:∵y=﹣0.2t2+1.4t﹣2=﹣0.2(t﹣3.5)2+4.5,
∴当t=3.5时,y最大=4.5,
则最佳加工时间为3.5h,
故选:C.
2.解:∵礼炮在点火升空到最高点引爆,
∴t=﹣=﹣=6,
∴从点火升空到引爆需要的时间为6s,
故选:D.
3.解:设该抛物线的对称轴为x,
由图象可得,
解得6<x<9,
故选:C.
4.解:①∵(﹣1,0),(3,0)和(0,3)坐标都满足函数y=|x2﹣2x﹣3|,
∴①是错误的;
②根据函数的图象和性质,发现当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大,因此②是正确的;
③由图象可知,当x<﹣1时,函数值随x的减小而增大,当x>3时,函数值随x的增大而增大,均存在大于顶点坐标的函数值,故当x=1时的函数值4并非最大值,故③错误.
④由图象可知,函数与直线y=m有4个公共点,则m的取值范围是0<m<4,故④正确.
故选:B.
5.解:由题意可得:A(﹣250,0),P(0,﹣100),
设抛物线解析式为:y=ax2﹣100,
则0=62500a﹣100,
解得:a=,
故抛物线解析式为:y=x2﹣100.
故答案为:y=x2﹣100.
6.解:设抛物线的解析式为y=a(x﹣6)2+3.2,
将点A(0,1.4)代入,得:36a+3.2=1.4,
解得:a=﹣0.05,
则抛物线的解析式为y=﹣0.05(x﹣6)2+3.2;
当y=0时,﹣0.05(x﹣6)2+3.2=0,
解得:x1=﹣2(舍),x2=14,
所以足球第一次落地点C距守门员14米.
故答案为:14.
7.解:设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
由题意:,
解得,
∴y=﹣x2,
当x=5时,y=﹣1,
故t==4(h),
答:再过4小时水位达到桥拱最高点O.
故答案为:4.
8.解:以AB所在的直线为x轴,以线段AB的垂直平分线所在的直线为y轴建立平面直角坐标系:
∴A(﹣30,0),B(30,0),D(15,150),
设抛物线的解析式为y=a(x+30)(x﹣30),将(15,150)代入,得:
150=a(15+30)(15﹣30),
解得:a=﹣,
∴y=﹣(x+30)(x﹣30)
=﹣x2+200,
∴抛物线顶端O的坐标为(0,200),
∴此抛物线顶端O到连桥AB距离为200m.
故答案为:200m.
9.解:(1)设这个隔离区一边AB长为x米,则另一边BC长为(8﹣x+1)米.
依题意,得x (8﹣x+1)=10,
解得x1=5,x2=4.
当x=5时,5>4.5(舍去),
当x=4时,(8﹣x+1)=2.5(米)<4.5米.
∴若面积为10平方米,隔离区的长为4米,宽为2.5米.
(2)隔离区有最大面积,理由如下:
由(1)知,隔离区的面积为x (8﹣x+1)=﹣x2+x=﹣(x﹣)2+,
∵﹣<0,
∴当x=时,隔离区有最大面积,最大面积为平方米.
10.解:(1)由题意可得,
y1=(26﹣a)(20+2a),
当a=5时,y1=(26﹣5)×(20+2×5)=630,
即当a=5时,y1的值是630;
(2)由题意可得,
y2=(20﹣b)(32+2b)=﹣2b2+8b+640,
即y2关于b的函数表达式为y2=﹣2b2+8b+640;
(3)设两家下降的价格都为x元,两家的盈利和为w元,
w=(26﹣x)(20+2x)+(﹣2x2+8x+640)=﹣4x2+40x+1160=﹣4(x﹣5)2+1260,
∴当x=5时,w取得最大值,此时w=1260,
答:每件科技产品下降5元时,两家分店一天的盈利和最大,最大是1260元.
【教学后测】
1.解:设一个旅行团的人数是x人,设营业额为y元,根据题意可得:
y=x[800﹣10(x﹣30)]
=﹣10x2+1100x
=﹣10(x2﹣110x)
=﹣10(x﹣55)2+30250,
故当一个旅行团的人数是55人时,这个旅行社可以获得最大的营业额.
故选:B.
2.解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴当x=0时,y=3,即OA=3m,故A选项正确,
当x=1时,y取得最大值,此时y=4,故B选项正确,C选项错误,
当y=0时,x=3或x=﹣1(舍去),故D选项正确,
故选:C.
3.解:∵y=﹣x2+6x=﹣x(x﹣6)(0≤x≤6),
∴A1(6,0),
∴整个函数图象每隔6×2=12个单位长度,函数值就相等,
∵18=12×1+6,
所以m的值等于x=6时的纵坐标,
所以m=﹣6×(6﹣6)=0.
故选:D.
4.解:设每天的利润为W元,根据题意,得:
W=(x﹣28)(80﹣y)﹣5000
=(x﹣28)[80﹣(x﹣42)]﹣5000
=﹣x2+129x﹣8416
=﹣(x﹣258)2+8225,
∵当x=258时,y=×258﹣42=22.5,不是整数,
∴当x=256或x=260时,函数取得最大值,最大值为8224元,
又∵想让客人得到实惠,
∴x=260(舍去)
∴宾馆应将房间定价确定为256元时,才能获得最大利润,
故答案为:256.
5.解:∵跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.
∴抛物线的对称轴为x=2.5,
∴x=﹣=2.5,解得:b=3,
∴抛物线为y=﹣x2+3x+1,
∵人梯到起跳点A的水平距离是4,
∴点B的横坐标为4,
则yB=﹣×42+3×4+1=3.4,即BC=3.4米.
故答案为:3.4.
6.解:(1)设线段OA的关系式为y=kx,
则12k=16,
解得k=,
所以y=x.
设线段AB的关系式为y=kx+b,
则,
解得k=﹣1,b=42,
所以y=﹣x+42;
当x=﹣x+42,
解得x=18,
所以m=18,
综上,y=;
(2)当18<x≤24时,
设p=kx+b,则,
解得k=0.5,b=3,
∴p=0.5x+3;
当0≤x≤18时,
,
∵,
∴w随x增大而增大,
∴当x=18时,w最大=96;
当18<x≤24时,
w=(0.5x+3﹣8)(﹣x+42)=﹣0.5x2+26x﹣210=﹣0.5(x﹣26)2+128,
∵a=﹣0.5<0,开口向下,
∴当x<26时,w随x的增大而增大,
∴当x=24时,w最大=126,
答:第24天时销售利润最大,最大为126元.
同课章节目录
