2022年中考二轮复习《利用函数关系解决实际问题》专题复习导学案(含答案)
文档属性
| 名称 | 2022年中考二轮复习《利用函数关系解决实际问题》专题复习导学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 341.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 16:12:31 | ||
图片预览



文档简介
利用函数关系解决问题
【教学前测】
1.如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
2.小杰把班级勤工俭学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本利和为y元,则y与x之间的函数关系式为( )
A.y=500(x+1)2 B.y=x2+500 C.y=x2+500x D.y=x2+5x
3.炮弹从炮口射出后,飞行的高度h(m)与飞行时间t(s)之间的函数关系式是h=V0tsinα-5t2,其中V0是炮弹发射的初速度,α是炮弹的发射角,当V0=300(m/s), α=30 时,炮弹飞行的最大高度是 m.
4.如图所示为抛物线形的桥拱,当拱顶离水面2 m时,水面宽4 m.若水面高度下降2 m,则水面宽度增加 m.
5.一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量y(升)关于加满油后已行驶的路程x(千米)的函数图象.
(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求y关于x的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
6.某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?
【课堂导学】
1.某工厂今年八月份医用防护服的产量是50万件,计划九月份和十月份增加产量,如果月平均增长率为x,那么十月份医用防护服的产量y(万件)与x之间的函数表达式为 .
2.从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是 .
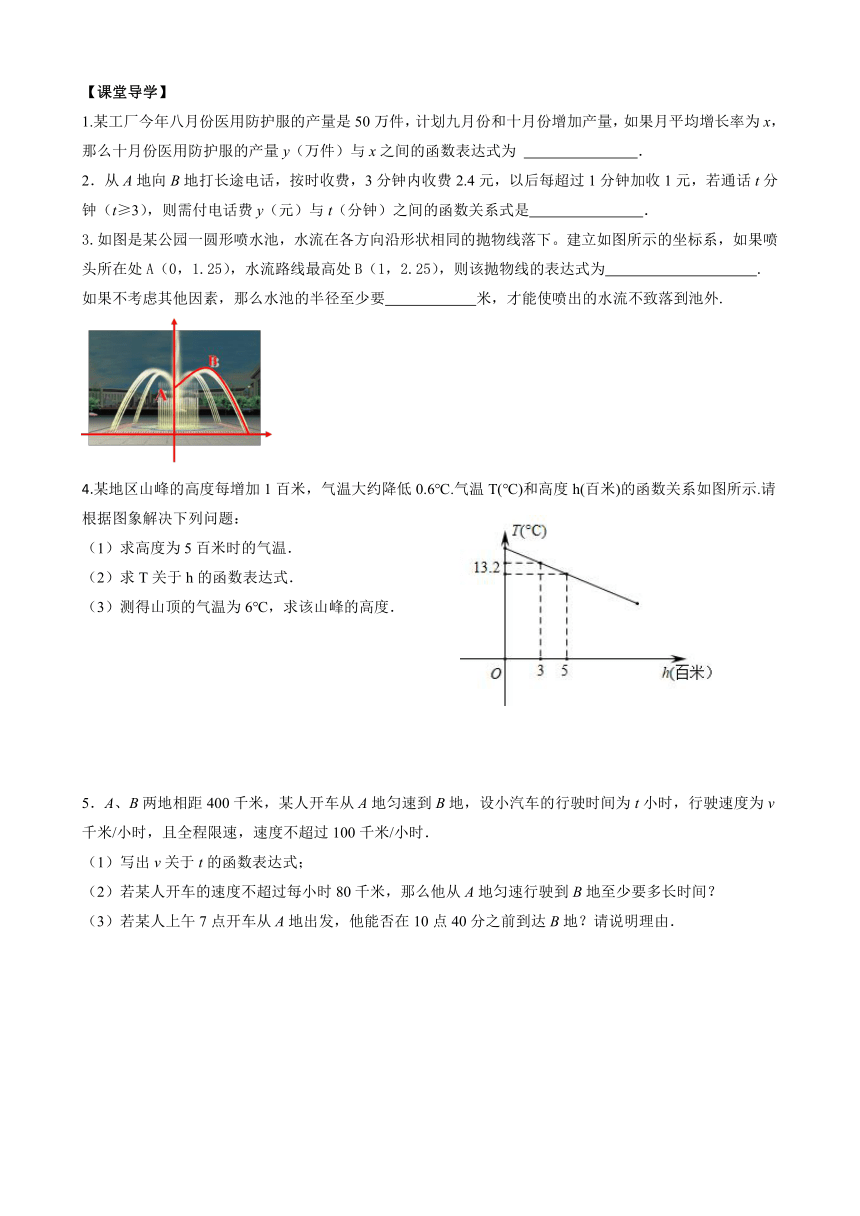
3.如图是某公园一圆形喷水池,水流在各方向沿形状相同的抛物线落下。建立如图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处B(1,2.25),则该抛物线的表达式为 .
如果不考虑其他因素,那么水池的半径至少要 米,才能使喷出的水流不致落到池外.
4.某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
5.A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.
(1)写出v关于t的函数表达式;
(2)若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?
(3)若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.
6.如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
7.如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,点P从点A开始沿AB边向点B以2厘米/秒的速度移动,点Q从点B开始沿BC边向点C以1厘米/秒的速度移动,如果P,Q分别从A,B同时出发,几秒后ΔPBQ的面积最大?最大面积是多少?
8.某超市销售一批日用品,每个进价为10元,经市场调研发现:该日用品每个售价为15元时,每天的销售量为200个,销售单价每提高1元,销售量就会减少8个,设销售单价为x(元),每天的销售量为y(个),每天的销售利润为W(元).
(1)直接写出销售量y与销售单价x之间的函数关系式;
(2)求当销售单价x定为多少元时,每天销售利润W最大?最大利润是多少元?
(3)若每天获得的利润不低于1288元,请直接写出销售单价x的取值范围.
【教学后测】
1.在某种病毒的传播过程中,每轮传染平均1人会传染x个人,若最初2个人感染该病毒,经过两轮传染,共有y人感染,则y与x的函数关系式为( )
A.y=2(1+x)2 B.y=(2+x)2 C.y=2+2x2 D.y=(1+2x)2
2.“元旦”期间,老李一家自驾游去了离家320千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
A.1.25小时 B.4小时 C.4.25小时 D.4.75小时
3.商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x为正整数),每星期销售的利润为y元,则y与x的函数关系式为( )
A.y=10(200﹣10x) B.y=200(10+x)
C.y=10(200﹣10x)2 D.y=(10+x)(200﹣10x)
4.经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表.
x 1 2 3 4 5 6
y 6 2.9 2 1.5 1.2 1
(1)请画出相应函数的图象,并求出函数表达式.
(2)点A(x1,y1),B(x2,y2)在此函数图象上.若x1<x2,
则y1,y2有怎样的大小关系?请说明理由.
5.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
利用函数关系解决问题
【教学前测】
1.C
2.A
3. 1125.
4. 4-4m.
5.解:(1)由图象可知:汽车行驶400千米,剩余油量30升,
∵行驶时的耗油量为0.1升/千米,则汽车行驶400千米,耗油400×0.1=40(升)
∴加满油时油箱的油量是40+30=70升.
(2)设y=kx+b(k≠0),
把(0,70),(400,300)坐标代入可得:k=﹣0.1,b=70
∴y=﹣0.1x+70,
当y=5 时,x=650
即已行驶的路程的为650千米.
6. 解:设每个涨价x元,那么y=(50+x-40)(500-10x)
=-10x2+400x+5000
=-10(x-20)2 +9000(0 ≤ x≤50 ,且为整数 )
答:定价为70元/个,利润最高为9000元.
【课堂导学】
1.
2.
3.,2.25
4.解:(1)由题意得 高度增加2百米,则温度降低2×0.6=1.2(℃).
∴13.2-1.2=12
∴高度为5百米时的气温大约是12℃.
(2)设T=-0.6h+b(k≠0),
当h=3时,T=13.2,
13.2=-0.63+b,
解得 b=15.
∴T=-0.6h+15.
(3)当T=6时,6=-0.6h+15,
解得h=15.
∴该山峰的高度大约为15百米.
5.解:(1)根据题意,路程为400,
设小汽车的行驶时间为t小时,行驶速度为v千米/小时,
则v关于t的函数表达式为v=;
(2)设从A地匀速行驶到B地要t小时,则≤80,
解得:t≥5,
∴他从A地匀速行驶到B地至少要5小时;
(3)∵v≤100,
≤100,
解得:t≥4,
∴某人从A地出发最少用4个小时才能到达B地,
7点至10点40分,是3小时,
∴他不能在10点40分之前到达B地.
6.解:(1) ∵ AB为x米、篱笆长为24米
∴ BC为(24-4x)米
∴ S=x(24-4x)=-4x2+24 x (0(2)当x= 时,S最大值==36(平方米)
(3) ∵墙的可用长度为8米
∴ 0<24-4x ≤8 解得 4≤x<6
∴当x=4m时,S最大值=32 平方米
7.解:根据题意,设经过x秒后ΔPBQ的面积y最大,则:
AP=2x cm ,PB=(8-2x ) cm ,QB=xcm
则 y=x(8-2x)=-x2+4x=-(x2 -4x+4-4)=-(x - 2)2 +4 (0所以,当P、Q同时运动2秒后ΔPBQ的面积y最大,最大面积是 4 cm2
8.解:(1)由题意得:y=200﹣8(x﹣15)=﹣8x+320,
∴销售量y与销售单价x之间的函数关系式y=﹣8x+320;
(2)由题意得:W=(x﹣10)y=(x﹣10)(﹣8x+320)=﹣8x2+400x﹣3200=﹣8(x﹣25)2+1800,
∵﹣8<0,
∴当x=25时,W有最大值,最大值为1800,
∴当销售单价定为25元时,每天销售利润W最大,最大利润是1800元;
(3)当W=1288时,﹣8(x﹣25)2+1800=1288,
解得:x1=17,x2=33,
∵W=﹣8(x﹣25)2+1800,﹣8<0,
∴抛物线开口向下,
∴当每天获得的利润不低于1288元时,17≤x≤33.
【教学后测】
1.A.
2.D.
3.D.
4.解:(1)函数图象如图所示,设函数表达式为,
把x=1,y=6代入,得k=6,
∴函数表达式为();
(2)∵k=6>0,
∴在第一象限,y随x的增大而减小,
∴0<x1<x2时,则y1>y2.
5.解:(1)设水柱所在抛物线(第一象限部分)的函数表达式为y=a(x﹣3)2+5(a≠0),将(8,0)代入y=a(x﹣3)2+5,得:25a+5=0,解得:a=﹣,∴水柱所在抛物线(第一象限部分)的函数表达式为y=﹣(x﹣3)2+5(0<x<8).
(2)当y=1.8时,有﹣(x﹣3)2+5=1.8,解得:x1=﹣1,x2=7,∴为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心7米以内.
(3)当x=0时,y=﹣(x﹣3)2+5=.
设改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣x2+bx+.
∵该函数图象过点(16,0),∴0=﹣×162+16b+,解得:b=3,∴改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣x2+3x+=﹣(x﹣)2+,∴扩建改造后喷水池水柱的最大高度为米.
【教学前测】
1.如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
2.小杰把班级勤工俭学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本利和为y元,则y与x之间的函数关系式为( )
A.y=500(x+1)2 B.y=x2+500 C.y=x2+500x D.y=x2+5x
3.炮弹从炮口射出后,飞行的高度h(m)与飞行时间t(s)之间的函数关系式是h=V0tsinα-5t2,其中V0是炮弹发射的初速度,α是炮弹的发射角,当V0=300(m/s), α=30 时,炮弹飞行的最大高度是 m.
4.如图所示为抛物线形的桥拱,当拱顶离水面2 m时,水面宽4 m.若水面高度下降2 m,则水面宽度增加 m.
5.一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量y(升)关于加满油后已行驶的路程x(千米)的函数图象.
(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求y关于x的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
6.某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?
【课堂导学】
1.某工厂今年八月份医用防护服的产量是50万件,计划九月份和十月份增加产量,如果月平均增长率为x,那么十月份医用防护服的产量y(万件)与x之间的函数表达式为 .
2.从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是 .
3.如图是某公园一圆形喷水池,水流在各方向沿形状相同的抛物线落下。建立如图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处B(1,2.25),则该抛物线的表达式为 .
如果不考虑其他因素,那么水池的半径至少要 米,才能使喷出的水流不致落到池外.
4.某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
5.A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.
(1)写出v关于t的函数表达式;
(2)若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?
(3)若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.
6.如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
7.如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,点P从点A开始沿AB边向点B以2厘米/秒的速度移动,点Q从点B开始沿BC边向点C以1厘米/秒的速度移动,如果P,Q分别从A,B同时出发,几秒后ΔPBQ的面积最大?最大面积是多少?
8.某超市销售一批日用品,每个进价为10元,经市场调研发现:该日用品每个售价为15元时,每天的销售量为200个,销售单价每提高1元,销售量就会减少8个,设销售单价为x(元),每天的销售量为y(个),每天的销售利润为W(元).
(1)直接写出销售量y与销售单价x之间的函数关系式;
(2)求当销售单价x定为多少元时,每天销售利润W最大?最大利润是多少元?
(3)若每天获得的利润不低于1288元,请直接写出销售单价x的取值范围.
【教学后测】
1.在某种病毒的传播过程中,每轮传染平均1人会传染x个人,若最初2个人感染该病毒,经过两轮传染,共有y人感染,则y与x的函数关系式为( )
A.y=2(1+x)2 B.y=(2+x)2 C.y=2+2x2 D.y=(1+2x)2
2.“元旦”期间,老李一家自驾游去了离家320千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
A.1.25小时 B.4小时 C.4.25小时 D.4.75小时
3.商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x为正整数),每星期销售的利润为y元,则y与x的函数关系式为( )
A.y=10(200﹣10x) B.y=200(10+x)
C.y=10(200﹣10x)2 D.y=(10+x)(200﹣10x)
4.经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表.
x 1 2 3 4 5 6
y 6 2.9 2 1.5 1.2 1
(1)请画出相应函数的图象,并求出函数表达式.
(2)点A(x1,y1),B(x2,y2)在此函数图象上.若x1<x2,
则y1,y2有怎样的大小关系?请说明理由.
5.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
利用函数关系解决问题
【教学前测】
1.C
2.A
3. 1125.
4. 4-4m.
5.解:(1)由图象可知:汽车行驶400千米,剩余油量30升,
∵行驶时的耗油量为0.1升/千米,则汽车行驶400千米,耗油400×0.1=40(升)
∴加满油时油箱的油量是40+30=70升.
(2)设y=kx+b(k≠0),
把(0,70),(400,300)坐标代入可得:k=﹣0.1,b=70
∴y=﹣0.1x+70,
当y=5 时,x=650
即已行驶的路程的为650千米.
6. 解:设每个涨价x元,那么y=(50+x-40)(500-10x)
=-10x2+400x+5000
=-10(x-20)2 +9000(0 ≤ x≤50 ,且为整数 )
答:定价为70元/个,利润最高为9000元.
【课堂导学】
1.
2.
3.,2.25
4.解:(1)由题意得 高度增加2百米,则温度降低2×0.6=1.2(℃).
∴13.2-1.2=12
∴高度为5百米时的气温大约是12℃.
(2)设T=-0.6h+b(k≠0),
当h=3时,T=13.2,
13.2=-0.63+b,
解得 b=15.
∴T=-0.6h+15.
(3)当T=6时,6=-0.6h+15,
解得h=15.
∴该山峰的高度大约为15百米.
5.解:(1)根据题意,路程为400,
设小汽车的行驶时间为t小时,行驶速度为v千米/小时,
则v关于t的函数表达式为v=;
(2)设从A地匀速行驶到B地要t小时,则≤80,
解得:t≥5,
∴他从A地匀速行驶到B地至少要5小时;
(3)∵v≤100,
≤100,
解得:t≥4,
∴某人从A地出发最少用4个小时才能到达B地,
7点至10点40分,是3小时,
∴他不能在10点40分之前到达B地.
6.解:(1) ∵ AB为x米、篱笆长为24米
∴ BC为(24-4x)米
∴ S=x(24-4x)=-4x2+24 x (0
(3) ∵墙的可用长度为8米
∴ 0<24-4x ≤8 解得 4≤x<6
∴当x=4m时,S最大值=32 平方米
7.解:根据题意,设经过x秒后ΔPBQ的面积y最大,则:
AP=2x cm ,PB=(8-2x ) cm ,QB=xcm
则 y=x(8-2x)=-x2+4x=-(x2 -4x+4-4)=-(x - 2)2 +4 (0
8.解:(1)由题意得:y=200﹣8(x﹣15)=﹣8x+320,
∴销售量y与销售单价x之间的函数关系式y=﹣8x+320;
(2)由题意得:W=(x﹣10)y=(x﹣10)(﹣8x+320)=﹣8x2+400x﹣3200=﹣8(x﹣25)2+1800,
∵﹣8<0,
∴当x=25时,W有最大值,最大值为1800,
∴当销售单价定为25元时,每天销售利润W最大,最大利润是1800元;
(3)当W=1288时,﹣8(x﹣25)2+1800=1288,
解得:x1=17,x2=33,
∵W=﹣8(x﹣25)2+1800,﹣8<0,
∴抛物线开口向下,
∴当每天获得的利润不低于1288元时,17≤x≤33.
【教学后测】
1.A.
2.D.
3.D.
4.解:(1)函数图象如图所示,设函数表达式为,
把x=1,y=6代入,得k=6,
∴函数表达式为();
(2)∵k=6>0,
∴在第一象限,y随x的增大而减小,
∴0<x1<x2时,则y1>y2.
5.解:(1)设水柱所在抛物线(第一象限部分)的函数表达式为y=a(x﹣3)2+5(a≠0),将(8,0)代入y=a(x﹣3)2+5,得:25a+5=0,解得:a=﹣,∴水柱所在抛物线(第一象限部分)的函数表达式为y=﹣(x﹣3)2+5(0<x<8).
(2)当y=1.8时,有﹣(x﹣3)2+5=1.8,解得:x1=﹣1,x2=7,∴为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心7米以内.
(3)当x=0时,y=﹣(x﹣3)2+5=.
设改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣x2+bx+.
∵该函数图象过点(16,0),∴0=﹣×162+16b+,解得:b=3,∴改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣x2+3x+=﹣(x﹣)2+,∴扩建改造后喷水池水柱的最大高度为米.
同课章节目录
