6.1.1平均数(1) 课件(共28张PPT)
文档属性
| 名称 | 6.1.1平均数(1) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 19:32:13 | ||
图片预览








文档简介
(共28张PPT)
6.1.1平均数(1)
第六章
数据的分析
2021-2022学年八年级数学上册同步课件
学习目标
1.理解数据的权和加权平均数的概念,体会权的作用。
2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法。
3.会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念。
导入新课
小松鼠对小马说:这条河平均水深1米,太危险了。小马说:我的身高已经长到1米5了,上一次都轻松过河了,这次就更没有问题了。
请问小马过河有危险么?
答:有危险。
平均水深不代表所有水深。例如:前半部分水深1米8,后半部分水深0.2米,平均水深也为1米。所以有危险。
讲授新课
算术平均数
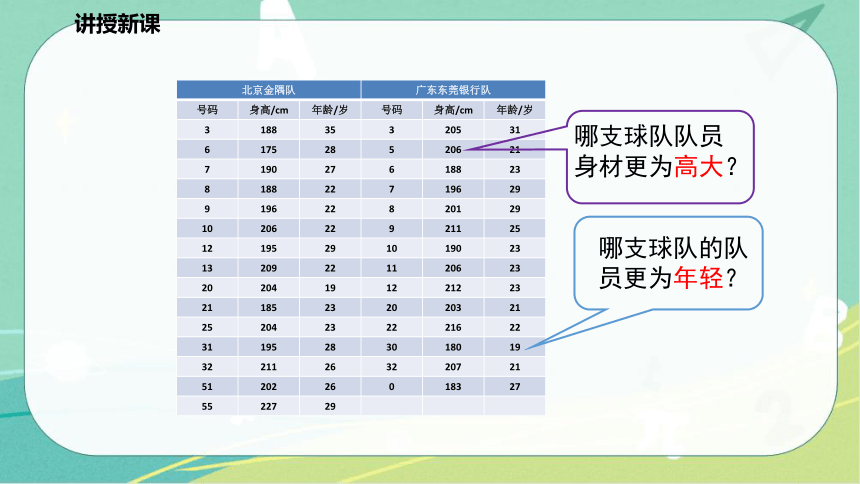
在篮球比赛中,队员的身高、年龄都是影响球队实力的因素,如何衡量两个球队队员的身高?
怎样理解“甲球队队员的身高比乙队更高”?怎样理解“甲队队员比乙队更年轻”?
讲授新课
北京金隅队 广东东莞银行队 号码 身高/cm 年龄/岁 号码 身高/cm 年龄/岁
3 188 35 3 205 31
6 175 28 5 206 21
7 190 27 6 188 23
8 188 22 7 196 29
9 196 22 8 201 29
10 206 22 9 211 25
12 195 29 10 190 23
13 209 22 11 206 23
20 204 19 12 212 23
21 185 23 20 203 21
25 204 23 22 216 22
31 195 28 30 180 19
32 211 26 32 207 21
51 202 26 0 183 27
55 227 29
哪支球队队员身材更为高大?
哪支球队的队员更为年轻?
讲授新课
北京金隅队的平均年龄
广东东莞银行队的平均年龄
所以广东东莞银行队的队员更为年轻.
=25.4 (岁),
≈24.1 (岁),
讲授新课
归纳总结
日常生活中,我们常用平均数表示一组数据的“平均水平”,它反映了一组数据的“集中趋势”.
记作:
x 读作:“x拔”
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数.
讲授新课
加权平均数
二
年龄/岁 19 22 23 26 27 28 29 35
相应的队员数 1 4 2 2 1 2 2 1
小明是这样计算北京金隅队队员的平均年龄的:
平均年龄 =(19×1+ 22×4+ 23×2+ 26×2+ 27×1+ 28×2+ 29×2+ 35×1)÷(1+4+2+2+1+2+2+1)
=25.4(岁)
小明的做法有道理吗?
讲授新课
如果在n个数中,x1出现 f1 次,x2出现 f2次,…,xk 出现 fk 次(这里f1+f2+… + fk =n),那么
当一组数据中有若干个数据多次重复出现时,可以考虑下面的做法:
讲授新课
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
测 试 项 目 测 试 成 绩 A B C
创 新
综合知识
语 言
72
50
88
85
74
45
67
70
67
某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
例
讲授新课
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
解:A的平均成绩为(72+50+88)÷3=70(分),
B的平均成绩为(85+74+45)÷3=68(分).
C的平均成绩为(67+70+67)÷3=68(分).
由70>68,故A将被录用.
这样选择好不好?
测 试 项 目 测 试 成 绩 A B C
创 新
综合知识
语 言
72
50
88
85
74
45
67
70
67
讲授新课
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩,此时谁将被录用?
解∶
A的测试成绩为∶(72×4+50×3+88×1)÷(4+3+1)=65.75(分),
B的测试成绩为∶(85×4+74×3+45×1)÷(4+3+1)=75.875(分),
C的测试成绩为∶(67×4+70×3+67×1)÷(4+3+1)=68.125(分).
因此候选人B将被录用.
为何结果不一样?
测 试 项 目 测 试 成 绩 A B C
创 新
综合知识
语 言
72
50
88
85
74
45
67
70
67
讲授新课
(1)(2)的结果不一样说明了什么?
思 考
实际问题中,一组数据的各个数据的“重要程度”未必相同.因此,在计算这组数据的平均数时,往往给每个数据一个“权”,如上例中的4就是创新的权、3是综合知识的权、1是语言的权 ,而称
为A的三项测试成绩的加权平均数.
讲授新课
归纳总结
一般地,若n个数x1, x2, …, xn的权分别是f1,f2,…,fn ,则
叫做这n个数的加权平均数.
权的意义:(1)数据的重要程度
(2)权衡轻重或份量大小
讲授新课
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
(1)如果这家公司想找一名综合能力较强的翻译,那听、说、读、写成绩按多少比确定?如何计算平均成绩,说明你的方法.
(2)如果公司要招聘一名笔译能力较强的翻译,那听、说、读、写成绩按2:1:3:4的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
例1 一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示:
讲授新课
因为79.5<80.4,所以应该录取乙.
因为80.25>79.5,所以应该录取甲.
解:(1)甲的平均成绩
(分),
乙的平均成绩
(分),
(2)甲的平均成绩
(分),
乙的平均成绩
(分),
讲授新课
(3)如果公司想招一名口语能力较强的翻译,则应该录取谁?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
听、说、读、写的成绩按照3:3:2:2的比确定.
解:通过计算比较,应该录取甲.
讲授新课
同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.
讨论 将问题(1)、(2)、(3)比较,你能体会到权的作用吗?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
数据的权能够反映数据的相对重要程度!
当堂检测
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
A.84 B. 86 C. 88 D. 90
2.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
A. (x+y)/2 B. (mx+ny)/(m+n)
C. (x+y)/(m+n) D. (mx+ny)/(x+y)
D
B
当堂检测
2.李大伯有一片果林,共有80棵果树.某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得10个果子,质量分别为(单位:㎏):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23.以此估算,李大伯收获的这批果子的单个质量和总质量分别约为( )
A.0.25 ㎏,200 ㎏ B.2.5 ㎏,100 ㎏
C.0.25 ㎏,100 ㎏ D.2.5 ㎏,200 ㎏
C
当堂检测
3.已知:x1,x2,x3,…, x10的平均数是a,x11,x12,x13,… ,x30
的平均数是b,则x1,x2,x3,… ,x30的平均数( )
A.(a+b) B.(a+b)
C.(a+3b)/3 D.(a+2b)/3
D
4.若x1,x2,…, xn的平均数为a,
(1)则数据x1+3,x2+3,…,xn+3的平均数为 .
(2)则数据10x1,10x2,… ,10xn 的平均数为 .
a+3
10a
当堂检测
5.一组数据为10, 8, 9, 12, 13, 10, 8,则这组数据的平均数是______.
6.已知x1, x2, x3, 3, 4, 7的平均数为6,则
x1+x2+x3=______.
10
22
7.若m个数的平均数为x, n个数的平均数为y, 则
(m+n)个数的平均数是( )
A.(x+y)/2 B.(x+y)/(m+n)
C.(mx+ny)/(x+y) D.(mx+ny)/(m+n)
D
当堂检测
8.甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每斤( )
A.3.87元 B.4.2元 C.4.3元 D.3.88元
9.某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为 ( )
A.60 B.62 C.70 D.无法确定
A
C
当堂检测
10.下表是校女子排球队队员的年龄分布:
年龄 13 14 15 16
频数 1 4 5 2
求校女子排球队队员的平均年龄.
答:校女子排球队队员的平均年龄为14.7岁.
解:
当堂检测
11.万载三中规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末成绩占50%.小桐的三项成绩(百分制)依次是95分、90分、85分,小桐这学期的体育成绩是多少?
答:小桐这学期的体育成绩是88.5分.
解:
(分).
课堂小结
平均数与加权平均数
算术平均数:
加权平均数:
(f( f1 + f2 + …+ fk =n)
https://www.21cnjy.com/help/help_extract.php
6.1.1平均数(1)
第六章
数据的分析
2021-2022学年八年级数学上册同步课件
学习目标
1.理解数据的权和加权平均数的概念,体会权的作用。
2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法。
3.会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念。
导入新课
小松鼠对小马说:这条河平均水深1米,太危险了。小马说:我的身高已经长到1米5了,上一次都轻松过河了,这次就更没有问题了。
请问小马过河有危险么?
答:有危险。
平均水深不代表所有水深。例如:前半部分水深1米8,后半部分水深0.2米,平均水深也为1米。所以有危险。
讲授新课
算术平均数
在篮球比赛中,队员的身高、年龄都是影响球队实力的因素,如何衡量两个球队队员的身高?
怎样理解“甲球队队员的身高比乙队更高”?怎样理解“甲队队员比乙队更年轻”?
讲授新课
北京金隅队 广东东莞银行队 号码 身高/cm 年龄/岁 号码 身高/cm 年龄/岁
3 188 35 3 205 31
6 175 28 5 206 21
7 190 27 6 188 23
8 188 22 7 196 29
9 196 22 8 201 29
10 206 22 9 211 25
12 195 29 10 190 23
13 209 22 11 206 23
20 204 19 12 212 23
21 185 23 20 203 21
25 204 23 22 216 22
31 195 28 30 180 19
32 211 26 32 207 21
51 202 26 0 183 27
55 227 29
哪支球队队员身材更为高大?
哪支球队的队员更为年轻?
讲授新课
北京金隅队的平均年龄
广东东莞银行队的平均年龄
所以广东东莞银行队的队员更为年轻.
=25.4 (岁),
≈24.1 (岁),
讲授新课
归纳总结
日常生活中,我们常用平均数表示一组数据的“平均水平”,它反映了一组数据的“集中趋势”.
记作:
x 读作:“x拔”
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数.
讲授新课
加权平均数
二
年龄/岁 19 22 23 26 27 28 29 35
相应的队员数 1 4 2 2 1 2 2 1
小明是这样计算北京金隅队队员的平均年龄的:
平均年龄 =(19×1+ 22×4+ 23×2+ 26×2+ 27×1+ 28×2+ 29×2+ 35×1)÷(1+4+2+2+1+2+2+1)
=25.4(岁)
小明的做法有道理吗?
讲授新课
如果在n个数中,x1出现 f1 次,x2出现 f2次,…,xk 出现 fk 次(这里f1+f2+… + fk =n),那么
当一组数据中有若干个数据多次重复出现时,可以考虑下面的做法:
讲授新课
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
测 试 项 目 测 试 成 绩 A B C
创 新
综合知识
语 言
72
50
88
85
74
45
67
70
67
某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
例
讲授新课
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
解:A的平均成绩为(72+50+88)÷3=70(分),
B的平均成绩为(85+74+45)÷3=68(分).
C的平均成绩为(67+70+67)÷3=68(分).
由70>68,故A将被录用.
这样选择好不好?
测 试 项 目 测 试 成 绩 A B C
创 新
综合知识
语 言
72
50
88
85
74
45
67
70
67
讲授新课
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩,此时谁将被录用?
解∶
A的测试成绩为∶(72×4+50×3+88×1)÷(4+3+1)=65.75(分),
B的测试成绩为∶(85×4+74×3+45×1)÷(4+3+1)=75.875(分),
C的测试成绩为∶(67×4+70×3+67×1)÷(4+3+1)=68.125(分).
因此候选人B将被录用.
为何结果不一样?
测 试 项 目 测 试 成 绩 A B C
创 新
综合知识
语 言
72
50
88
85
74
45
67
70
67
讲授新课
(1)(2)的结果不一样说明了什么?
思 考
实际问题中,一组数据的各个数据的“重要程度”未必相同.因此,在计算这组数据的平均数时,往往给每个数据一个“权”,如上例中的4就是创新的权、3是综合知识的权、1是语言的权 ,而称
为A的三项测试成绩的加权平均数.
讲授新课
归纳总结
一般地,若n个数x1, x2, …, xn的权分别是f1,f2,…,fn ,则
叫做这n个数的加权平均数.
权的意义:(1)数据的重要程度
(2)权衡轻重或份量大小
讲授新课
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
(1)如果这家公司想找一名综合能力较强的翻译,那听、说、读、写成绩按多少比确定?如何计算平均成绩,说明你的方法.
(2)如果公司要招聘一名笔译能力较强的翻译,那听、说、读、写成绩按2:1:3:4的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
例1 一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示:
讲授新课
因为79.5<80.4,所以应该录取乙.
因为80.25>79.5,所以应该录取甲.
解:(1)甲的平均成绩
(分),
乙的平均成绩
(分),
(2)甲的平均成绩
(分),
乙的平均成绩
(分),
讲授新课
(3)如果公司想招一名口语能力较强的翻译,则应该录取谁?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
听、说、读、写的成绩按照3:3:2:2的比确定.
解:通过计算比较,应该录取甲.
讲授新课
同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.
讨论 将问题(1)、(2)、(3)比较,你能体会到权的作用吗?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
数据的权能够反映数据的相对重要程度!
当堂检测
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
A.84 B. 86 C. 88 D. 90
2.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
A. (x+y)/2 B. (mx+ny)/(m+n)
C. (x+y)/(m+n) D. (mx+ny)/(x+y)
D
B
当堂检测
2.李大伯有一片果林,共有80棵果树.某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得10个果子,质量分别为(单位:㎏):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23.以此估算,李大伯收获的这批果子的单个质量和总质量分别约为( )
A.0.25 ㎏,200 ㎏ B.2.5 ㎏,100 ㎏
C.0.25 ㎏,100 ㎏ D.2.5 ㎏,200 ㎏
C
当堂检测
3.已知:x1,x2,x3,…, x10的平均数是a,x11,x12,x13,… ,x30
的平均数是b,则x1,x2,x3,… ,x30的平均数( )
A.(a+b) B.(a+b)
C.(a+3b)/3 D.(a+2b)/3
D
4.若x1,x2,…, xn的平均数为a,
(1)则数据x1+3,x2+3,…,xn+3的平均数为 .
(2)则数据10x1,10x2,… ,10xn 的平均数为 .
a+3
10a
当堂检测
5.一组数据为10, 8, 9, 12, 13, 10, 8,则这组数据的平均数是______.
6.已知x1, x2, x3, 3, 4, 7的平均数为6,则
x1+x2+x3=______.
10
22
7.若m个数的平均数为x, n个数的平均数为y, 则
(m+n)个数的平均数是( )
A.(x+y)/2 B.(x+y)/(m+n)
C.(mx+ny)/(x+y) D.(mx+ny)/(m+n)
D
当堂检测
8.甲、乙、丙三种饼干售价分别为3元、4元、5元,若将甲种10斤、乙种8斤、丙种7斤混到一起,则售价应该定为每斤( )
A.3.87元 B.4.2元 C.4.3元 D.3.88元
9.某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为 ( )
A.60 B.62 C.70 D.无法确定
A
C
当堂检测
10.下表是校女子排球队队员的年龄分布:
年龄 13 14 15 16
频数 1 4 5 2
求校女子排球队队员的平均年龄.
答:校女子排球队队员的平均年龄为14.7岁.
解:
当堂检测
11.万载三中规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末成绩占50%.小桐的三项成绩(百分制)依次是95分、90分、85分,小桐这学期的体育成绩是多少?
答:小桐这学期的体育成绩是88.5分.
解:
(分).
课堂小结
平均数与加权平均数
算术平均数:
加权平均数:
(f( f1 + f2 + …+ fk =n)
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
