6.4.2数据的离散程度(2) 课件(共24张PPT)
文档属性
| 名称 | 6.4.2数据的离散程度(2) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 976.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 19:34:07 | ||
图片预览






文档简介
(共24张PPT)
6.4.2数据的离散程度(2)
第六章
数据的分析
2021-2022学年八年级数学上册同步课件
学习目标
1.通过更为丰富的例子,让学生较为全面地理解方差及其在现实生活中的应用。
2.通过实例,让学生体会数据的离散程度在现实生活中广泛存在,应视情况分析方差或标准差对于问题的影响。
导入新课
极差是指一组数据中最大数据与最小数据的差。
方差是各个数据与平均数之差的平方的平均数。
标准差就是方差的算术平方根.
讲授新课
方差的应用
一
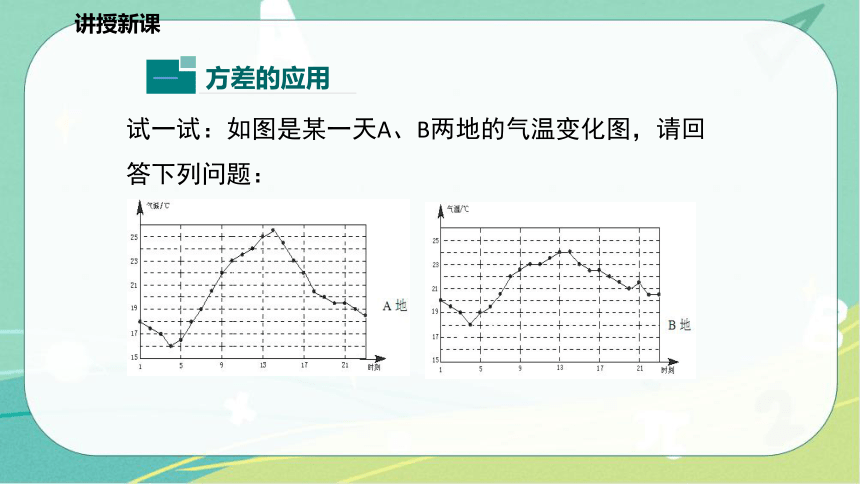
试一试:如图是某一天A、B两地的气温变化图,请回答下列问题:
讲授新课
(1)不进行计算,说说A、B两地这一天气候的特点
(2)分别计算这一天A、B两地气温的平均数和方差,与你刚才的看法一致吗?
A、B两地平均气温相近,但A地日温差较大,B地日温差较小.
A地平均气温20.42 ℃,方差7.76;
B地平均气温21.35 ℃,方差2.78.
一组数据的方差越小,这组数据就越稳定,那么,是不是方差越小就表示这组数据越好呢?
讲授新课
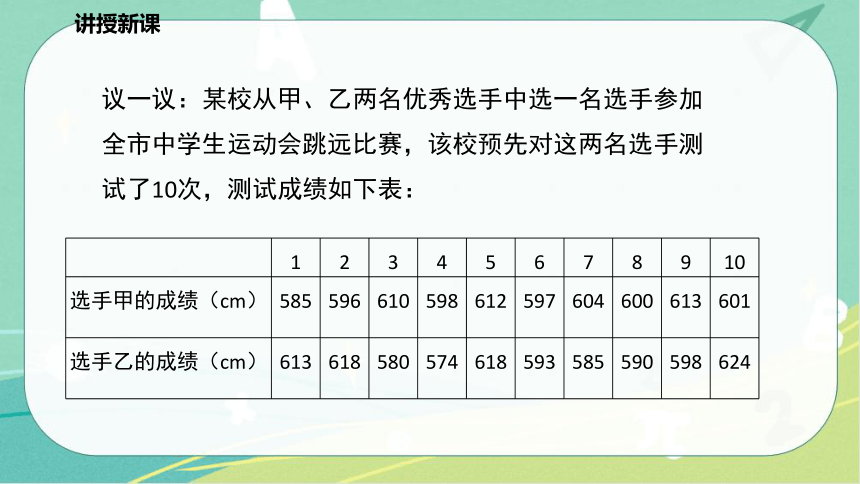
议一议:某校从甲、乙两名优秀选手中选一名选手参加全市中学生运动会跳远比赛,该校预先对这两名选手测试了10次,测试成绩如下表:
1 2 3 4 5 6 7 8 9 10
选手甲的成绩(cm) 585 596 610 598 612 597 604 600 613 601
选手乙的成绩(cm) 613 618 580 574 618 593 585 590 598 624
讲授新课
(1)他们的平均成绩分别是多少?
(2)甲、乙这10次比赛成绩的方差分别是多少?
(3)这两名运动员的运动成绩各有什么特点?
甲601.6 cm,乙599.3 cm。
甲65.84,乙284.21.
甲运动员成绩较稳定,因为极差、方差都比较小
甲的平均成绩比乙好
乙较有潜质,因为乙的最远成绩比甲的最远成绩好
讲授新课
(4)历届比赛表明,成绩达到596cm就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?
(5)如果历届比赛表明,成绩达到610cm就能打破记录,你认为为了打破记录应选谁参加这项比赛?
在10次比赛中,甲运动员有9次超过596cm,而乙仅有5次,因此一般应选甲运动员参加这项比赛。
若要打破610cm的跳远记录,则一般应选乙运动员。
讲授新课
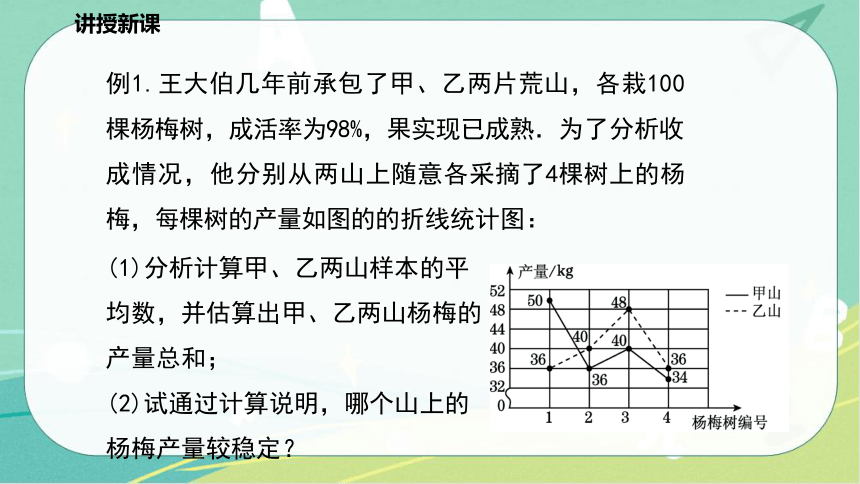
例1.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活率为98%,果实现已成熟.为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵树的产量如图的的折线统计图:
(1)分析计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
讲授新课
解:(1)甲山上4棵杨梅树的产量分别为50 kg、36 kg、40 kg、34 kg,所以甲山杨梅产量的样本平均数为 =40(kg).
乙山上4棵杨梅树的产量分别为36 kg、40 kg、48 kg、36 kg,所以乙山杨梅产量的样本平均数为
=40(kg).
讲授新课
(2)s甲= =
s乙= =
因为s甲>s乙,所以乙山上的杨梅产量较稳定.
甲、乙两山杨梅的产量总和约为2×100×98%×40=7840(kg).
讲授新课
甲团
163
164
164
165
165
166
166
167
乙团
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
例 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都
表演了舞剧《天鹅湖》,参加表演的女演员的身高(单
位:cm)分别是:
讲授新课
解: 甲乙两团演员的身高更分别是:
由
可知甲芭蕾舞团女演员的身高更整齐.
讲授新课
(1)在解决实际问题时,方差的作用是什么?
反映数据的波动大小.方差越大,数据的波动越大;
方差越小,数据的波动越小,可用样本方差估计总体方差.
(2)运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数相等或相近时,再利用样本方差来估计总体数据的波动情况.
归纳总结
当堂检测
1.学校准备从甲、乙、丙、丁四名同学中选择一名同学代表学校参加市里举办的“汉字听写”大赛,四名同学平时成绩的平均数 (单位:分)及方差s2如下表所示:
如果要选出一个成绩好且状态稳定的同学参赛,那么应该选择的同学是 .
甲 乙 丙 丁
94 98 98 96
s2 1 1.2 1 1.8
丙
当堂检测
2.申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表.
分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1)
当堂检测
解:A组数据的新数为:0.6,1.9,0.5,-1.3,-0.2,-0.3;
B组数据的新数为:0,0.8,1.1,-0.6,-1.1,-0.2.
×(0.6+1.9+0.5-1.3-0.2-0.3)=0.2(百万元);
×(0+0.8+1.1-0.6-1.1-0.2)=0(百万元).
s2A= ×[(0.2-0.6)2+(0.2-1.9)2+(0.2-0.5)2+(0.2+1.3)2+
(0.2+0.2)2+(0.2+0.3)2]≈0.97(百万元2);
s2B = ×[02+0.82+1.12+0.62+1.12+0.22]≈0.6(百万元2).
这两个方差的大小反映了A,B两家餐饮店相邻两天的日营业额的变化情况,并且B餐饮店相邻两天的日营业额的变化情况比较小.
当堂检测
3.某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下:
经过计算,甲进球的平均数为 =8,方差为 .
队员 每人每天进球数 甲 10 6 10 6 8
乙 7 9 7 8 9
当堂检测
(1)求乙进球的平均数和方差;
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
解:
乙进球的平均数为 ,
(1)
方差为 .
(2)
我认为应该选乙队员去参加3分球投篮大赛.
因为甲乙的平均成绩一样,
所以 说明乙队员进球数更稳定.
当堂检测
4.甲、乙两班各有8名学生参加数学竞赛,成绩如下表:
甲 65 74 70 80 65 66 69 71
乙 60 75 78 61 80 62 65 79
请比较两班学生成绩的优劣.
当堂检测
解:
所以从平均分看两个班一样,
从方差看
甲班的成绩比较稳定.
但是从高分看,80分都是1人,75分以上的甲班只有1人,而乙班有4人,占总数的一半,可见乙班成绩优于甲班.
综上可知,可见乙班成绩优于甲班.
课堂小结
根据方差做决策
方差的作用:比较数据的稳定性
利用方差解答实际问题
https://www.21cnjy.com/help/help_extract.php
6.4.2数据的离散程度(2)
第六章
数据的分析
2021-2022学年八年级数学上册同步课件
学习目标
1.通过更为丰富的例子,让学生较为全面地理解方差及其在现实生活中的应用。
2.通过实例,让学生体会数据的离散程度在现实生活中广泛存在,应视情况分析方差或标准差对于问题的影响。
导入新课
极差是指一组数据中最大数据与最小数据的差。
方差是各个数据与平均数之差的平方的平均数。
标准差就是方差的算术平方根.
讲授新课
方差的应用
一
试一试:如图是某一天A、B两地的气温变化图,请回答下列问题:
讲授新课
(1)不进行计算,说说A、B两地这一天气候的特点
(2)分别计算这一天A、B两地气温的平均数和方差,与你刚才的看法一致吗?
A、B两地平均气温相近,但A地日温差较大,B地日温差较小.
A地平均气温20.42 ℃,方差7.76;
B地平均气温21.35 ℃,方差2.78.
一组数据的方差越小,这组数据就越稳定,那么,是不是方差越小就表示这组数据越好呢?
讲授新课
议一议:某校从甲、乙两名优秀选手中选一名选手参加全市中学生运动会跳远比赛,该校预先对这两名选手测试了10次,测试成绩如下表:
1 2 3 4 5 6 7 8 9 10
选手甲的成绩(cm) 585 596 610 598 612 597 604 600 613 601
选手乙的成绩(cm) 613 618 580 574 618 593 585 590 598 624
讲授新课
(1)他们的平均成绩分别是多少?
(2)甲、乙这10次比赛成绩的方差分别是多少?
(3)这两名运动员的运动成绩各有什么特点?
甲601.6 cm,乙599.3 cm。
甲65.84,乙284.21.
甲运动员成绩较稳定,因为极差、方差都比较小
甲的平均成绩比乙好
乙较有潜质,因为乙的最远成绩比甲的最远成绩好
讲授新课
(4)历届比赛表明,成绩达到596cm就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?
(5)如果历届比赛表明,成绩达到610cm就能打破记录,你认为为了打破记录应选谁参加这项比赛?
在10次比赛中,甲运动员有9次超过596cm,而乙仅有5次,因此一般应选甲运动员参加这项比赛。
若要打破610cm的跳远记录,则一般应选乙运动员。
讲授新课
例1.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活率为98%,果实现已成熟.为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵树的产量如图的的折线统计图:
(1)分析计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
讲授新课
解:(1)甲山上4棵杨梅树的产量分别为50 kg、36 kg、40 kg、34 kg,所以甲山杨梅产量的样本平均数为 =40(kg).
乙山上4棵杨梅树的产量分别为36 kg、40 kg、48 kg、36 kg,所以乙山杨梅产量的样本平均数为
=40(kg).
讲授新课
(2)s甲= =
s乙= =
因为s甲>s乙,所以乙山上的杨梅产量较稳定.
甲、乙两山杨梅的产量总和约为2×100×98%×40=7840(kg).
讲授新课
甲团
163
164
164
165
165
166
166
167
乙团
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
例 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都
表演了舞剧《天鹅湖》,参加表演的女演员的身高(单
位:cm)分别是:
讲授新课
解: 甲乙两团演员的身高更分别是:
由
可知甲芭蕾舞团女演员的身高更整齐.
讲授新课
(1)在解决实际问题时,方差的作用是什么?
反映数据的波动大小.方差越大,数据的波动越大;
方差越小,数据的波动越小,可用样本方差估计总体方差.
(2)运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数相等或相近时,再利用样本方差来估计总体数据的波动情况.
归纳总结
当堂检测
1.学校准备从甲、乙、丙、丁四名同学中选择一名同学代表学校参加市里举办的“汉字听写”大赛,四名同学平时成绩的平均数 (单位:分)及方差s2如下表所示:
如果要选出一个成绩好且状态稳定的同学参赛,那么应该选择的同学是 .
甲 乙 丙 丁
94 98 98 96
s2 1 1.2 1 1.8
丙
当堂检测
2.申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表.
分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1)
当堂检测
解:A组数据的新数为:0.6,1.9,0.5,-1.3,-0.2,-0.3;
B组数据的新数为:0,0.8,1.1,-0.6,-1.1,-0.2.
×(0.6+1.9+0.5-1.3-0.2-0.3)=0.2(百万元);
×(0+0.8+1.1-0.6-1.1-0.2)=0(百万元).
s2A= ×[(0.2-0.6)2+(0.2-1.9)2+(0.2-0.5)2+(0.2+1.3)2+
(0.2+0.2)2+(0.2+0.3)2]≈0.97(百万元2);
s2B = ×[02+0.82+1.12+0.62+1.12+0.22]≈0.6(百万元2).
这两个方差的大小反映了A,B两家餐饮店相邻两天的日营业额的变化情况,并且B餐饮店相邻两天的日营业额的变化情况比较小.
当堂检测
3.某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下:
经过计算,甲进球的平均数为 =8,方差为 .
队员 每人每天进球数 甲 10 6 10 6 8
乙 7 9 7 8 9
当堂检测
(1)求乙进球的平均数和方差;
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
解:
乙进球的平均数为 ,
(1)
方差为 .
(2)
我认为应该选乙队员去参加3分球投篮大赛.
因为甲乙的平均成绩一样,
所以 说明乙队员进球数更稳定.
当堂检测
4.甲、乙两班各有8名学生参加数学竞赛,成绩如下表:
甲 65 74 70 80 65 66 69 71
乙 60 75 78 61 80 62 65 79
请比较两班学生成绩的优劣.
当堂检测
解:
所以从平均分看两个班一样,
从方差看
甲班的成绩比较稳定.
但是从高分看,80分都是1人,75分以上的甲班只有1人,而乙班有4人,占总数的一半,可见乙班成绩优于甲班.
综上可知,可见乙班成绩优于甲班.
课堂小结
根据方差做决策
方差的作用:比较数据的稳定性
利用方差解答实际问题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
