6.3从统计图分析数据的集中趋势 课件(共31张PPT)
文档属性
| 名称 | 6.3从统计图分析数据的集中趋势 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 19:35:06 | ||
图片预览











文档简介
(共31张PPT)
6.3从统计图分析数据的集中趋势
第六章
数据的分析
2021-2022学年八年级数学上册同步课件
学习目标
1.掌握扇形统计图、折线统计图、条形统计图的特点,并通过看统计图估计一组数据的平均数。
2.能读取各种统计图中的信息,通过信息计算平均数、中位数、众数。
3.掌握描述一组数据集中趋势的方法,能用统计知识解决实际问题。
导入新课
从前面的学习内容我们知道,平均数、中位数和众数都是用来代表一组数据的,那么在统计图中我们如何分析数据的集中趋势呢?又如何进行正确的估计呢?
导入新课
体现各项的具体数目
反映事物的变化趋势
表示各部分所占的百分比
我们学习过的统计图都有哪些?各自的特点呢?
讲授新课
从折线统计图分析数据的集中趋势
一
例.为了检查面包的质量是否达标,随机抽取了同种规格的面包10个,这10个面包的质量如图所示.这10个面包质量的众数是多少?你能估计出一个这样的面包的平均质量吗?你是怎么估计的?
讲授新课
因为折线统计图具有能够显示数据的变化趋势,反映事物的变化情况的特点,所以利用折线统计图比较容易看出数据的众数,也比较容易求出数据的中位数和平均数.
讲授新课
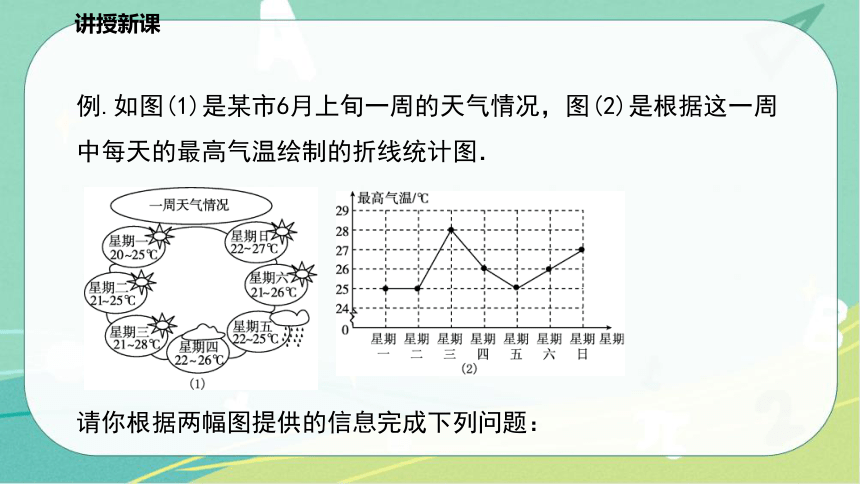
例.如图(1)是某市6月上旬一周的天气情况,图(2)是根据这一周中每天的最高气温绘制的折线统计图.
请你根据两幅图提供的信息完成下列问题:
讲授新课
(1)这一周中温差最大的一天是星期________;
(2)这一周中每天最高气温的众数是____℃,中位数是___℃,
平均数是___℃;
(3)这两幅图各有特点,而关于折线统计图的优点,下列四句话中描述最贴切的一句是___.(填序号)
①可以清楚地告诉我们每天天气情况;②可以清楚地告诉我们各
部分数量占总量的百分比的情况;③可以直观地告诉我们这一周
每天最高气温的变化情况;④可以清楚地告诉我们这一周每天气
温的总体情况.
三
25
26
26
③
讲授新课
在折线统计图中,可以怎样求一组数据的众数、中位数、平均数?
众数:同一水平线上出现次数最多的数据;
中位数:从上到下(或从下到上)找中间点所对的数;
平均数:读出各类数据,按平均数公式计算.
归纳总结
讲授新课
例:小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示:
(1)在这名同学中,本学期计划购买课外书的花费的众数是多少?
(2)计算这20名同学计划购买课外书的平均花费。
(1)众数是50元。
平均花费是57元
从扇形统计图分析数据的集中趋势
二
讲授新课
在上面的问题中,如果不知道调查的总人数,你还能求平均数吗
因为扇形统计图能看出部分在总体中所占的百分比,所以利用扇形统计图更容易看出数据的众数;利用加权平均数的求法可以求出数据的平均数.
讲授新课
例.某地连续统计了 10天日最高气温,并绘制成如图所示的扇形统计图.
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值.
解:(1)根据扇形统计图,35℃占的比
例最大,因此日平均气温的众数是35℃;
(2)这10天日最高气温的平均值是:32×10%+33×20%+34× 20%+35×30%+36×20%=34.3(℃).
讲授新课
扇形统计图中,圆中各扇形代表总体的不同部分,因此可直观的认为扇形大,则对应的部分所占百分比就大;扇形小,则对应的部分所占百分比就小.
在扇形统计图中,可以怎样求一组数据的众数、中位数、平均数?
归纳总结
讲授新课
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
(1) 从图中可以看出:
甲队队员年龄的众数是 ,中位数是 ;
乙队队员年龄的众数是 ,中位数是 ;
丙队队员年龄的众数是 ,中位数是 .
20岁
20岁
19岁
19岁
21岁
21岁
从条形统计图分析数据的集中趋势
三
讲授新课
(2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?与同伴交流.
甲队队员平均年龄为20,乙队队员平均年龄为约为19,丙队队员平均年龄约为21
(3)请你计算出三支球队队员的平均年龄,看看你上面的
估计是否准确?(分组进行计算)
答:甲、乙、丙三队队员的平均年龄依次是:20岁、19.3岁、20.6岁.
讲授新课
条形统计图能清楚的表示每个项目的具体数目,直条越高,对应具体数目就越多.
在条形统计图中,可以怎样求一组数据的众数、中位数、平均数呢?
归纳总结
讲授新课
从折线统计图中读取 从条形统计图中读取 从扇形统计图中读取
众数 同一水平线上出现次数最多的数据 最高的直条所对的横轴上的数就是众数 所占比例最大部分对应数就是众数
中位数 从左到右处于中间点所对应的数 从左到右处于中间点所对应的数 按从小到大顺序计算所占百分比之和,找到50%和51%对应部分的平均数就是中位数
平均数 从统计图中读出各类数据,按平均数的计算公式计算即可 从统计图中读出各类数据,按平均数的计算公式计算即可 从统计图中读出各类数据,按平均数的计算公式计算即可
归纳总结
讲授新课
例 甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
讲授新课
根据以上信息,整理分析数据如下:
平均成绩(环) 中位数(环) 众数(环)
甲 a 7 7
乙 7 b 8
(1)写出表格中a,b的值;
解:(1)a=7,b=7.5
(2)分别运用表中的三个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
解:(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多.综合以上各因素,若选派一名学生参赛的话,可选择乙参赛,因为乙获得高分的可能更大.
讲授新课
当堂检测
1.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表:
跳高成绩(m) 1.50 1.55 1.60 1.65 1.70 1.75
跳高人数 1 3 2 3 5 1
这些运动员跳高成绩的中位数和众数分别是( )
A.1.65,1.70 B.1.70,1.65
C.1.70,1.70 D.3,5
A
当堂检测
2.为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图.根据图中提供的信息,这50人一周的体育锻炼时间的众数和中位数分别是 ( )
A.6小时、6小时
B.6小时、4小时
C.4小时、4小时
D.4小时、6小时
A
当堂检测
3.某校为了解全校同学五一假期参加社团活动的情况 ,抽查了100名同学,统计他们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
A.4~6小时
B.6~8小时
C.8~10小时
D.不能确定
B
当堂检测
4.在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
A.众数是90
B.中位数是90
C.平均数是90
D.最高分与最低分的差是15
C
当堂检测
5. 如图,①是某城市三月份1至10月份的最低气温随时间变化的图象.
这10天最低气温的众数是 0C,最低气温的中位数是 0C, 最低气温的平均数是 0C。
①
2
0
0
当堂检测
6.如图是根据今年某校八年级学生体育考试跳绳的成绩绘制成的统计图.如果该校八年级共有200名学生参加了这项跳绳考试,根据该统计图给出的信息可得这些同学跳绳考试的平均成绩为________.
175.5
当堂检测
7.某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了如图所示的统计表:
零花钱数额(元) 5 10 15 20
学生人数(人) a 15 20 5
请根据表中的信息回答以下问题:
(1)求a的值;
(2)求这50名学生每人一周内的零花钱数额的众数和平均数.
解:(1)a=10
(2)这50名学生每人一周内的零花钱数额的众数是15,平均数是12
当堂检测
8.有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况:
请你根据图中信息回答下列问题:
(1)两次测试最低分在哪一次测试中?
(2)哪一次测试较容易?
(3)第一次测试中,中位数在哪一个分数段?第二次测试中,中位数在哪一个分数段?
解:(1)最低分在第一次测试中 (2)第二次 (3)20~39;40~59
课堂小结
从统计图分析数据的集中趋势
折线统计图
条形统计图
扇形统计图
https://www.21cnjy.com/help/help_extract.php
6.3从统计图分析数据的集中趋势
第六章
数据的分析
2021-2022学年八年级数学上册同步课件
学习目标
1.掌握扇形统计图、折线统计图、条形统计图的特点,并通过看统计图估计一组数据的平均数。
2.能读取各种统计图中的信息,通过信息计算平均数、中位数、众数。
3.掌握描述一组数据集中趋势的方法,能用统计知识解决实际问题。
导入新课
从前面的学习内容我们知道,平均数、中位数和众数都是用来代表一组数据的,那么在统计图中我们如何分析数据的集中趋势呢?又如何进行正确的估计呢?
导入新课
体现各项的具体数目
反映事物的变化趋势
表示各部分所占的百分比
我们学习过的统计图都有哪些?各自的特点呢?
讲授新课
从折线统计图分析数据的集中趋势
一
例.为了检查面包的质量是否达标,随机抽取了同种规格的面包10个,这10个面包的质量如图所示.这10个面包质量的众数是多少?你能估计出一个这样的面包的平均质量吗?你是怎么估计的?
讲授新课
因为折线统计图具有能够显示数据的变化趋势,反映事物的变化情况的特点,所以利用折线统计图比较容易看出数据的众数,也比较容易求出数据的中位数和平均数.
讲授新课
例.如图(1)是某市6月上旬一周的天气情况,图(2)是根据这一周中每天的最高气温绘制的折线统计图.
请你根据两幅图提供的信息完成下列问题:
讲授新课
(1)这一周中温差最大的一天是星期________;
(2)这一周中每天最高气温的众数是____℃,中位数是___℃,
平均数是___℃;
(3)这两幅图各有特点,而关于折线统计图的优点,下列四句话中描述最贴切的一句是___.(填序号)
①可以清楚地告诉我们每天天气情况;②可以清楚地告诉我们各
部分数量占总量的百分比的情况;③可以直观地告诉我们这一周
每天最高气温的变化情况;④可以清楚地告诉我们这一周每天气
温的总体情况.
三
25
26
26
③
讲授新课
在折线统计图中,可以怎样求一组数据的众数、中位数、平均数?
众数:同一水平线上出现次数最多的数据;
中位数:从上到下(或从下到上)找中间点所对的数;
平均数:读出各类数据,按平均数公式计算.
归纳总结
讲授新课
例:小明调查了班级里20名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示:
(1)在这名同学中,本学期计划购买课外书的花费的众数是多少?
(2)计算这20名同学计划购买课外书的平均花费。
(1)众数是50元。
平均花费是57元
从扇形统计图分析数据的集中趋势
二
讲授新课
在上面的问题中,如果不知道调查的总人数,你还能求平均数吗
因为扇形统计图能看出部分在总体中所占的百分比,所以利用扇形统计图更容易看出数据的众数;利用加权平均数的求法可以求出数据的平均数.
讲授新课
例.某地连续统计了 10天日最高气温,并绘制成如图所示的扇形统计图.
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值.
解:(1)根据扇形统计图,35℃占的比
例最大,因此日平均气温的众数是35℃;
(2)这10天日最高气温的平均值是:32×10%+33×20%+34× 20%+35×30%+36×20%=34.3(℃).
讲授新课
扇形统计图中,圆中各扇形代表总体的不同部分,因此可直观的认为扇形大,则对应的部分所占百分比就大;扇形小,则对应的部分所占百分比就小.
在扇形统计图中,可以怎样求一组数据的众数、中位数、平均数?
归纳总结
讲授新课
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
(1) 从图中可以看出:
甲队队员年龄的众数是 ,中位数是 ;
乙队队员年龄的众数是 ,中位数是 ;
丙队队员年龄的众数是 ,中位数是 .
20岁
20岁
19岁
19岁
21岁
21岁
从条形统计图分析数据的集中趋势
三
讲授新课
(2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?与同伴交流.
甲队队员平均年龄为20,乙队队员平均年龄为约为19,丙队队员平均年龄约为21
(3)请你计算出三支球队队员的平均年龄,看看你上面的
估计是否准确?(分组进行计算)
答:甲、乙、丙三队队员的平均年龄依次是:20岁、19.3岁、20.6岁.
讲授新课
条形统计图能清楚的表示每个项目的具体数目,直条越高,对应具体数目就越多.
在条形统计图中,可以怎样求一组数据的众数、中位数、平均数呢?
归纳总结
讲授新课
从折线统计图中读取 从条形统计图中读取 从扇形统计图中读取
众数 同一水平线上出现次数最多的数据 最高的直条所对的横轴上的数就是众数 所占比例最大部分对应数就是众数
中位数 从左到右处于中间点所对应的数 从左到右处于中间点所对应的数 按从小到大顺序计算所占百分比之和,找到50%和51%对应部分的平均数就是中位数
平均数 从统计图中读出各类数据,按平均数的计算公式计算即可 从统计图中读出各类数据,按平均数的计算公式计算即可 从统计图中读出各类数据,按平均数的计算公式计算即可
归纳总结
讲授新课
例 甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
讲授新课
根据以上信息,整理分析数据如下:
平均成绩(环) 中位数(环) 众数(环)
甲 a 7 7
乙 7 b 8
(1)写出表格中a,b的值;
解:(1)a=7,b=7.5
(2)分别运用表中的三个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
解:(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多.综合以上各因素,若选派一名学生参赛的话,可选择乙参赛,因为乙获得高分的可能更大.
讲授新课
当堂检测
1.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表:
跳高成绩(m) 1.50 1.55 1.60 1.65 1.70 1.75
跳高人数 1 3 2 3 5 1
这些运动员跳高成绩的中位数和众数分别是( )
A.1.65,1.70 B.1.70,1.65
C.1.70,1.70 D.3,5
A
当堂检测
2.为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图.根据图中提供的信息,这50人一周的体育锻炼时间的众数和中位数分别是 ( )
A.6小时、6小时
B.6小时、4小时
C.4小时、4小时
D.4小时、6小时
A
当堂检测
3.某校为了解全校同学五一假期参加社团活动的情况 ,抽查了100名同学,统计他们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
A.4~6小时
B.6~8小时
C.8~10小时
D.不能确定
B
当堂检测
4.在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
A.众数是90
B.中位数是90
C.平均数是90
D.最高分与最低分的差是15
C
当堂检测
5. 如图,①是某城市三月份1至10月份的最低气温随时间变化的图象.
这10天最低气温的众数是 0C,最低气温的中位数是 0C, 最低气温的平均数是 0C。
①
2
0
0
当堂检测
6.如图是根据今年某校八年级学生体育考试跳绳的成绩绘制成的统计图.如果该校八年级共有200名学生参加了这项跳绳考试,根据该统计图给出的信息可得这些同学跳绳考试的平均成绩为________.
175.5
当堂检测
7.某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了如图所示的统计表:
零花钱数额(元) 5 10 15 20
学生人数(人) a 15 20 5
请根据表中的信息回答以下问题:
(1)求a的值;
(2)求这50名学生每人一周内的零花钱数额的众数和平均数.
解:(1)a=10
(2)这50名学生每人一周内的零花钱数额的众数是15,平均数是12
当堂检测
8.有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况:
请你根据图中信息回答下列问题:
(1)两次测试最低分在哪一次测试中?
(2)哪一次测试较容易?
(3)第一次测试中,中位数在哪一个分数段?第二次测试中,中位数在哪一个分数段?
解:(1)最低分在第一次测试中 (2)第二次 (3)20~39;40~59
课堂小结
从统计图分析数据的集中趋势
折线统计图
条形统计图
扇形统计图
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
