人教版八年级数学 下册 第十九章 19.1.2 函数的图像 同步练习题(含答案)
文档属性
| 名称 | 人教版八年级数学 下册 第十九章 19.1.2 函数的图像 同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 205.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-22 19:28:35 | ||
图片预览

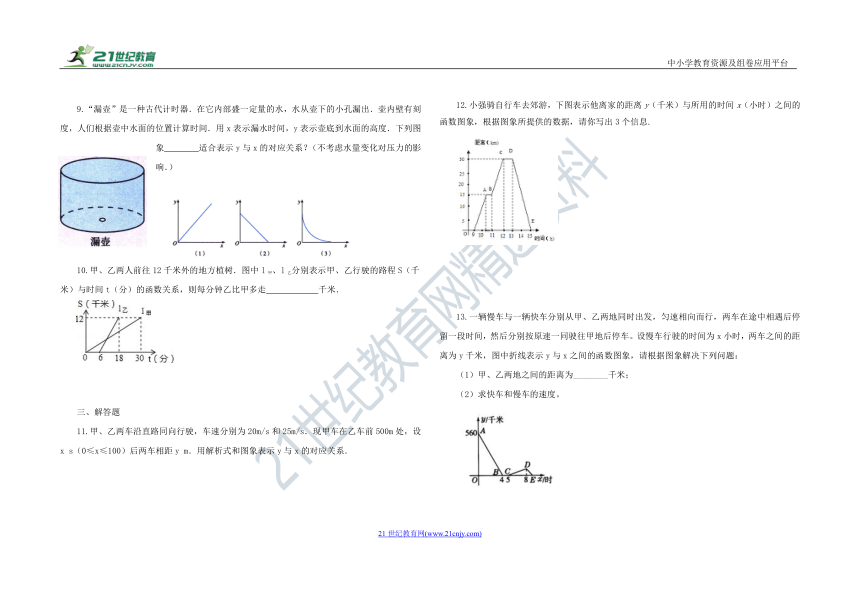
文档简介
中小学教育资源及组卷应用平台
第十九章 变量与函数
19.1.2 函数的图像
一、选择题
1.图中,表示y是x的函数图象是( )
2.如图,△ABC中,已知BC=16,高AD=10,动点C′由点C沿CB向点B移动(不与点B重合).设CC′的长为x,△ABC′的面积为S,则S与x之间的函数关系式为( )
A.S=80﹣5x B.S=5x C.S=10x D.S=5x+80
3.下列给出的四个点中,在函数y=3x+1的图像上的是( )
A.(1,4) B.(0,-1) C.(2,-7) D.(-1,2)
4.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这支蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).
如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中正确的是( )
B点表示此时快车到达乙地
B﹣C﹣D段表示慢车先加速后减速最后到达甲地
快车的速度为km/h
慢车的速度为125km/h
填空题
6.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ;自变量x的取值范围是 .
7.某物体从上午7时至下午4时的温度M(℃)是时间t(h)的函数: (其中t=0表示中午12时,t=-1表示上午11时,t=1表示13时),则上午10时此物体的温度为 ℃
8.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系的图象如图所示,则休息后园林队绿化面积为 平方米.
9.“漏壶”是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度.下列图象 适合表示y与x的对应关系?(不考虑水量变化对压力的影响.)
10.甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走 千米.
三、解答题
11.甲、乙两车沿直路同向行驶,车速分别为20m/s和25m/s.现甲车在乙车前500m处,设x s(0≤x≤100)后两车相距y m.用解析式和图象表示y与x的对应关系.
12.小强骑自行车去郊游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间的函数图象,根据图象所提供的数据,请你写出3个信息.
13.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后停留一段时间,然后分别按原速一同驶往甲地后停车。设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲、乙两地之间的距离为________千米;
(2)求快车和慢车的速度。
14.在同一直角坐标系中分别画出函数y=x与的图象.利用这两个图象回答:
(1)x取什么值时,x比大?
(2)x取什么值时,x比小?
15.李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下来聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a、b、c的值;
(2)求李老师从学校到家的总时间.
16.下面是小林画出函数的一部分图象,利用图象回答:
(1)自变量x的取值范围.
(2)当x取什么值时,y的最小值.最大值各是多少?
(3)在图中,当x增大时,y的值是怎样变化?
17.某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
18.请你编写一个故事,使故事情境中出现的一对变量x、y满足图所示的函数关系,要求:
(1)指出变量x和y的含义;
(2)利用图中的数据说明这对变量变化过程的实际意义,其中需涉及“速度”这个量.
参考答案:
一、1.C 2.A 3.A 4.C 5.C
二、6.Q=30-0.5x0≤x≤60
7.102
8.100
9.(2)
10.
三、11.y=500-5x(0≤x≤100).
12.解:(1)小强在离家30km处停留1h
(2)小强回家时速度为15km/h
(3)此次出行共耗费6h
13.分析:(1)甲、乙两地之间的距离为未出发时两车之间的距离;(2)抓住两点:①是相同而行,所行路程和=所行时间×速度和;②是快车行完全程用了8-1=7(小时).
解:(1)根据x,y的实际意义以及图像可知,甲、乙两地之间的距离是560千米.
(2)由图象可知,两车4小时相遇,相遇后停留了1小时,然后快车行驶3小时到达价低(点D表示快车到达甲地的时刻,此时慢车仍在返回的途中行驶).
∴快车的速度=560÷7=80(千米/时),
慢车的速度=(560-80×4)÷4=60(千米/时).
点拨:与行程有关的图象信息题中如果要求速度,一定要从图中读到一定的时间内路程的变化,用路程的变化除以时间的变化即为速度.相遇、追及问题中路程、速度、时间之间的关系要注意.
14.(1)-1<x<0或x>1;
(2)x<-1或0<x<1.
15.解:(1)由题意得b=2000-900=1100,
a=900÷45=20
c=20+30=50
(2)由C-D时,所用时间为1100÷110=10分钟
故总时间为c+10=50+10=60分钟
答:李老师从学校到家的总时间为60分钟.
16.解(1)0<x<10
(2)由图象得,当x=0时,y最大,此时y=10;
当x=10时,y最小,此时y=5.
(3)当x增大时,y减小.
17.解:(1)1000 25
(2)吃早餐公用了20-10=10分钟
(3)吃早餐前速度为500÷10=50米/分,
吃早餐后速度为(1000-500)÷5=100米/分.
18.解:本题答案不唯一,下列解法供参考.
(1)该函数图象表示小明骑车离出发地的距离y(单位:km)与他所用的时间x(单位:min)的关系.
(2)小明以0.4 km/min的速度匀速骑了5 min,原地休息了6 min后,以0.5 km/min的速度匀速骑车回出发地.
21世纪教育网(www.21cnjy.com)
第十九章 变量与函数
19.1.2 函数的图像
一、选择题
1.图中,表示y是x的函数图象是( )
2.如图,△ABC中,已知BC=16,高AD=10,动点C′由点C沿CB向点B移动(不与点B重合).设CC′的长为x,△ABC′的面积为S,则S与x之间的函数关系式为( )
A.S=80﹣5x B.S=5x C.S=10x D.S=5x+80
3.下列给出的四个点中,在函数y=3x+1的图像上的是( )
A.(1,4) B.(0,-1) C.(2,-7) D.(-1,2)
4.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这支蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).
如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中正确的是( )
B点表示此时快车到达乙地
B﹣C﹣D段表示慢车先加速后减速最后到达甲地
快车的速度为km/h
慢车的速度为125km/h
填空题
6.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ;自变量x的取值范围是 .
7.某物体从上午7时至下午4时的温度M(℃)是时间t(h)的函数: (其中t=0表示中午12时,t=-1表示上午11时,t=1表示13时),则上午10时此物体的温度为 ℃
8.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系的图象如图所示,则休息后园林队绿化面积为 平方米.
9.“漏壶”是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度.下列图象 适合表示y与x的对应关系?(不考虑水量变化对压力的影响.)
10.甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走 千米.
三、解答题
11.甲、乙两车沿直路同向行驶,车速分别为20m/s和25m/s.现甲车在乙车前500m处,设x s(0≤x≤100)后两车相距y m.用解析式和图象表示y与x的对应关系.
12.小强骑自行车去郊游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间的函数图象,根据图象所提供的数据,请你写出3个信息.
13.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后停留一段时间,然后分别按原速一同驶往甲地后停车。设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲、乙两地之间的距离为________千米;
(2)求快车和慢车的速度。
14.在同一直角坐标系中分别画出函数y=x与的图象.利用这两个图象回答:
(1)x取什么值时,x比大?
(2)x取什么值时,x比小?
15.李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下来聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a、b、c的值;
(2)求李老师从学校到家的总时间.
16.下面是小林画出函数的一部分图象,利用图象回答:
(1)自变量x的取值范围.
(2)当x取什么值时,y的最小值.最大值各是多少?
(3)在图中,当x增大时,y的值是怎样变化?
17.某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
18.请你编写一个故事,使故事情境中出现的一对变量x、y满足图所示的函数关系,要求:
(1)指出变量x和y的含义;
(2)利用图中的数据说明这对变量变化过程的实际意义,其中需涉及“速度”这个量.
参考答案:
一、1.C 2.A 3.A 4.C 5.C
二、6.Q=30-0.5x0≤x≤60
7.102
8.100
9.(2)
10.
三、11.y=500-5x(0≤x≤100).
12.解:(1)小强在离家30km处停留1h
(2)小强回家时速度为15km/h
(3)此次出行共耗费6h
13.分析:(1)甲、乙两地之间的距离为未出发时两车之间的距离;(2)抓住两点:①是相同而行,所行路程和=所行时间×速度和;②是快车行完全程用了8-1=7(小时).
解:(1)根据x,y的实际意义以及图像可知,甲、乙两地之间的距离是560千米.
(2)由图象可知,两车4小时相遇,相遇后停留了1小时,然后快车行驶3小时到达价低(点D表示快车到达甲地的时刻,此时慢车仍在返回的途中行驶).
∴快车的速度=560÷7=80(千米/时),
慢车的速度=(560-80×4)÷4=60(千米/时).
点拨:与行程有关的图象信息题中如果要求速度,一定要从图中读到一定的时间内路程的变化,用路程的变化除以时间的变化即为速度.相遇、追及问题中路程、速度、时间之间的关系要注意.
14.(1)-1<x<0或x>1;
(2)x<-1或0<x<1.
15.解:(1)由题意得b=2000-900=1100,
a=900÷45=20
c=20+30=50
(2)由C-D时,所用时间为1100÷110=10分钟
故总时间为c+10=50+10=60分钟
答:李老师从学校到家的总时间为60分钟.
16.解(1)0<x<10
(2)由图象得,当x=0时,y最大,此时y=10;
当x=10时,y最小,此时y=5.
(3)当x增大时,y减小.
17.解:(1)1000 25
(2)吃早餐公用了20-10=10分钟
(3)吃早餐前速度为500÷10=50米/分,
吃早餐后速度为(1000-500)÷5=100米/分.
18.解:本题答案不唯一,下列解法供参考.
(1)该函数图象表示小明骑车离出发地的距离y(单位:km)与他所用的时间x(单位:min)的关系.
(2)小明以0.4 km/min的速度匀速骑了5 min,原地休息了6 min后,以0.5 km/min的速度匀速骑车回出发地.
21世纪教育网(www.21cnjy.com)
