江西省上饶县中学2013届高三第二次月考数学(文)试题(零班、特长班)
文档属性
| 名称 | 江西省上饶县中学2013届高三第二次月考数学(文)试题(零班、特长班) |  | |
| 格式 | zip | ||
| 文件大小 | 305.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-19 20:15:41 | ||
图片预览



文档简介
上饶县中学2013届高三第二次月考数学(文)试题
(零班、特长班)
一.选择题(本大题共有10个小题,每小题5分,共50分)
1、已知,复数,若为纯虚数,则复数的虚部为
A.1 B. C. D.0
2、定义集合运算:,设A={1,2},B={0,2},
则集合A*B的所有元素之和为
A. 6 B. 3 C. 2 D. 0
3、已知:关于的不等式的解集是,:,则是的
A. 充分非必要条件 B. 必要非充分条件
C. 充分必要条件 D. 既非充分又非必要条件
4、设与(且≠2)具有不同的单调性,则与的大小关系是
A.MN D.M≤N
5、如果实数满足条件 ,那么的最大值为
A. B. C. D.
6、同时具有性质:①对任意,恒成立;②图象关于直线对称;
③在上是增函数的函数可以是
A. B.
C. D.
7、△ABC中,O为中线AM上一个动点,若AM=2,则的最小值为
A.-4 B.4 C. 2 D.-2
8、在各项均为正数的数列{}中,为前项和,且,
则=
A.- B. C.- D.
9、如果函数的图像关于点中心对称,那么的最小值为
A. B. C. D.
10、定义方程的实数根x0叫做函数的“新驻点”,如果函数,,()的“新驻点”分别为,,,那么,,的大小关系是
A.>> B.>> C.>> D.>>
二、填空题(每小题5分,共25分)
11、不等式的解集为
12、已知,且,则
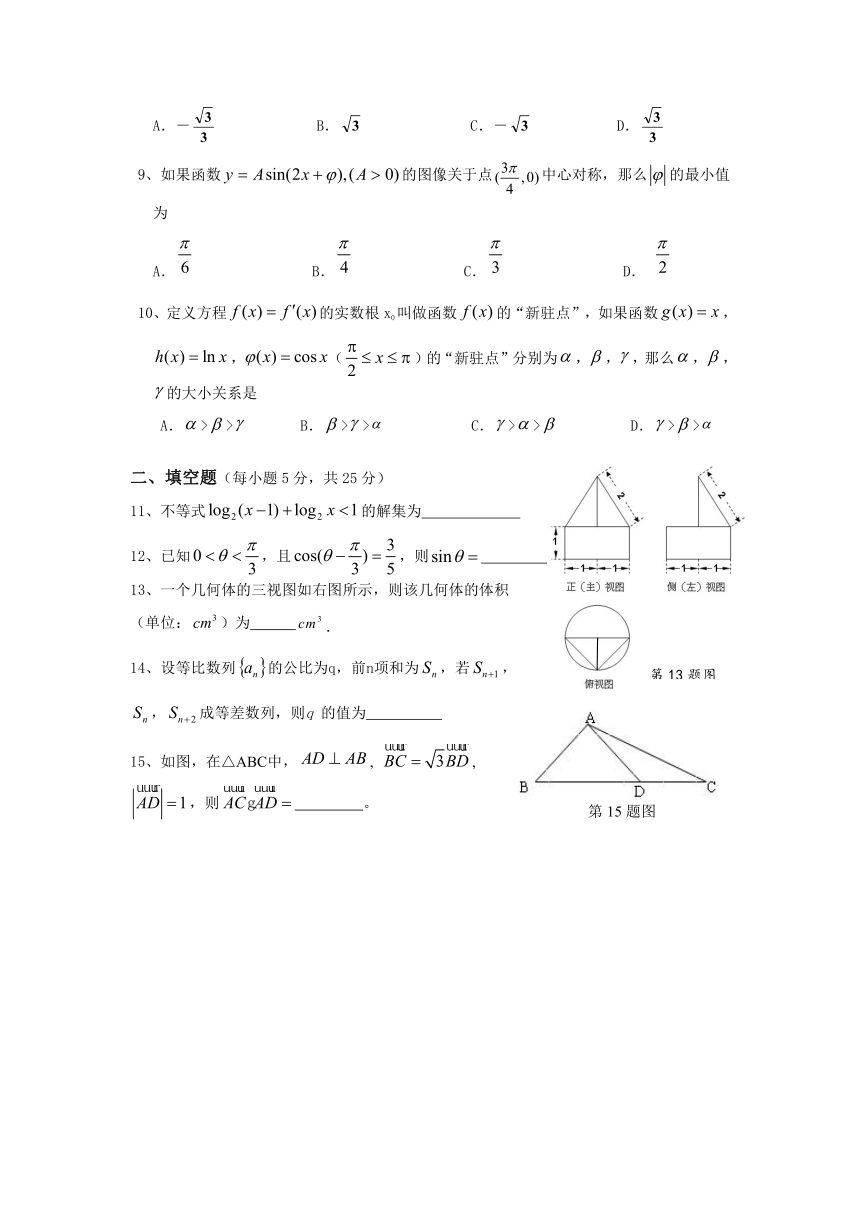
13、一个几何体的三视图如右图所示,则该几何体的体积
(单位:)为 .
14、设等比数列的公比为q,前n项和为,若,
,成等差数列,则q 的值为
15、如图,在△ABC中,, ,
,则 。
上饶县中学高三年级第二次月考
座位号
数 学 答 题 卡(文零、特)
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题
11、 12、 13、
14、 15、
三.解答题(本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.)
16.(本小题满分12分)
在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足
(Ⅰ)求角C的大小;
(Ⅱ)求的最大值。
17.(本小题满分12分)
已知等差数列。
(1)求数列的通项公式;
(2)若数列,当n为何值时,.
18.(本小题满分12分)
已知函数。
(Ⅰ)若曲线在处的切线平行于直线,求函数的单调区间;
(Ⅱ)若a >0,且对时,恒成立,求实数a的取值范围。
19.(本小题满分12分)
如图,在几何体中,
四边形为矩形,平面,。
(1)当时,求证:平面平面;
(2)若与所成角为45°,求几何体
的体积。
20.(本小题满分13分)
(1)已知是正常数,,,求证:,指出等号成立的条件;(2)利用(1)的结论求函数()的最小值,指出取最小值时的值.
21.(本小题满分14分)
设函数,函数y=f(x)-x有唯一的零点,其中实数a为常数,
(Ⅰ)求的表达式;
(Ⅱ)求的值;
(Ⅲ)若且,求证: .
高三数学第二次月考试卷
参 考 答 案(文零、特)
三、解答题(75分)解答应写文字说明,证明过程或演算步骤。
16 (Ⅰ)解:由题意可知 absinC=2abcosC.
所以tanC=. ………………4分
因为0所以C=. ………………6分
(Ⅱ)解:由已知sinA+sinB=sinA+sin(-C-A)=sinA+sin(-A)
=sinA+cosA+sinA=sin(A+)≤.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是. ………………12分
19、解:(1)当时,四边形是正方形,则 ……2分
∵平面,,∴ ……4分
又,∴平面,
∴平面平面. ……6分
(2)若与成角,,则. ……8分
∵,,
∴平面,
∴ ……10分
∴,∴
∴几何体的体积为 ……12分
20、(1)证:要证:
(2)
21、解:(1)由于,
-------2分当且仅当时,函数有唯一零点.
从而 -------4分
(2)由已知,得 -------5分
,即
数列是以为首项,为公差的等差数列. -------6分
,
,,即
(零班、特长班)
一.选择题(本大题共有10个小题,每小题5分,共50分)
1、已知,复数,若为纯虚数,则复数的虚部为
A.1 B. C. D.0
2、定义集合运算:,设A={1,2},B={0,2},
则集合A*B的所有元素之和为
A. 6 B. 3 C. 2 D. 0
3、已知:关于的不等式的解集是,:,则是的
A. 充分非必要条件 B. 必要非充分条件
C. 充分必要条件 D. 既非充分又非必要条件
4、设与(且≠2)具有不同的单调性,则与的大小关系是
A.M
5、如果实数满足条件 ,那么的最大值为
A. B. C. D.
6、同时具有性质:①对任意,恒成立;②图象关于直线对称;
③在上是增函数的函数可以是
A. B.
C. D.
7、△ABC中,O为中线AM上一个动点,若AM=2,则的最小值为
A.-4 B.4 C. 2 D.-2
8、在各项均为正数的数列{}中,为前项和,且,
则=
A.- B. C.- D.
9、如果函数的图像关于点中心对称,那么的最小值为
A. B. C. D.
10、定义方程的实数根x0叫做函数的“新驻点”,如果函数,,()的“新驻点”分别为,,,那么,,的大小关系是
A.>> B.>> C.>> D.>>
二、填空题(每小题5分,共25分)
11、不等式的解集为
12、已知,且,则
13、一个几何体的三视图如右图所示,则该几何体的体积
(单位:)为 .
14、设等比数列的公比为q,前n项和为,若,
,成等差数列,则q 的值为
15、如图,在△ABC中,, ,
,则 。
上饶县中学高三年级第二次月考
座位号
数 学 答 题 卡(文零、特)
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题
11、 12、 13、
14、 15、
三.解答题(本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.)
16.(本小题满分12分)
在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足
(Ⅰ)求角C的大小;
(Ⅱ)求的最大值。
17.(本小题满分12分)
已知等差数列。
(1)求数列的通项公式;
(2)若数列,当n为何值时,.
18.(本小题满分12分)
已知函数。
(Ⅰ)若曲线在处的切线平行于直线,求函数的单调区间;
(Ⅱ)若a >0,且对时,恒成立,求实数a的取值范围。
19.(本小题满分12分)
如图,在几何体中,
四边形为矩形,平面,。
(1)当时,求证:平面平面;
(2)若与所成角为45°,求几何体
的体积。
20.(本小题满分13分)
(1)已知是正常数,,,求证:,指出等号成立的条件;(2)利用(1)的结论求函数()的最小值,指出取最小值时的值.
21.(本小题满分14分)
设函数,函数y=f(x)-x有唯一的零点,其中实数a为常数,
(Ⅰ)求的表达式;
(Ⅱ)求的值;
(Ⅲ)若且,求证: .
高三数学第二次月考试卷
参 考 答 案(文零、特)
三、解答题(75分)解答应写文字说明,证明过程或演算步骤。
16 (Ⅰ)解:由题意可知 absinC=2abcosC.
所以tanC=. ………………4分
因为0
(Ⅱ)解:由已知sinA+sinB=sinA+sin(-C-A)=sinA+sin(-A)
=sinA+cosA+sinA=sin(A+)≤.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是. ………………12分
19、解:(1)当时,四边形是正方形,则 ……2分
∵平面,,∴ ……4分
又,∴平面,
∴平面平面. ……6分
(2)若与成角,,则. ……8分
∵,,
∴平面,
∴ ……10分
∴,∴
∴几何体的体积为 ……12分
20、(1)证:要证:
(2)
21、解:(1)由于,
-------2分当且仅当时,函数有唯一零点.
从而 -------4分
(2)由已知,得 -------5分
,即
数列是以为首项,为公差的等差数列. -------6分
,
,,即
同课章节目录
