【寒假衔接】北师大版 七年级数学下册4.5利用三角形全等测距离 预习检测卷(word版、含答案)
文档属性
| 名称 | 【寒假衔接】北师大版 七年级数学下册4.5利用三角形全等测距离 预习检测卷(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 488.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 10:43:00 | ||
图片预览



文档简介
【寒假衔接】北师大版 七年级数学下册
第四章 5.利用三角形全等测距离(预习检测卷)
一、选择题(共9题)
如图,为估计池塘岸边 , 两点间的距离,小方在池塘的一侧选取一点 ,测得 ,,, 间的距离不可能是
A. B. C. D.
把等腰直角三角形纸板 按如图所示的方式直立在桌面上,顶点 顶着桌面,若另外两个顶点与桌面的距离分别为 和 ,过另外两个顶点向桌面作垂线,则两个垂足之间的距离 为
A. B. C. D.无法确定
一块三角形玻璃样板不慎被张宇同学碰破了,成为四块完整碎片(如图所示),聪明的他经过仔细考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列选项中可行的是
A.带 , 或 , 去就可以了
B.带 , 或 , 去就可以了
C.带 , 或 , 去就可以了
D.带其中的任意两块去都可以
如图,为了测量点 到河对面的目标 之间的距离,在点 同侧选择了一点 ,测得 ,.然后在点 处立了标杆,使 ,,得到 ,测得 的长就是 , 两点间的距离.这里判定 的理由是
A. B. C. D.
如图,点 在 的延长线上,则下列条件中,不能判定 的是
A. B.
C. D.
如图,要测量河两岸相对的两点 , 的距离,先在 的垂线 上取两点 ,,使 ,再作出 的垂线 ,使点 ,, 在同一条直线上,可以证明 ,得到 ,因此测得 的长就是 的长,判定 最恰当的理由是
A. B. C. D.
把等腰 按如图所示立放在桌上,顶点 顶着桌面,若另两个顶点 , 距离桌面的距离分别是 和 ,垂足分别是 ,,则垂足之间的距离 的长为
A. B. C. D.求不出来
要测量河岸相对两点 , 的距离,已知 垂直于河岸 ,先在 上取两点 ,,使 ,再过点 作 的垂线段 ,使点 ,, 在一条直线上,如图,测出 ,,则 的长是
A. B. C. D.以上都不对
如图是人字形金属屋架的示意图.该屋架由 、 、 、 四段金属材料焊接而成,其中 、 、 、 四点均为焊接点,且 , 为 的中点.假设焊接所需的四段金属材料已截好,并已标出 段的中点 .那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及所选的焊接点是 .
A. 和 ,焊接点 B. 和 ,焊接点
C. 和 ,焊接点 D. 和 ,焊接点
二、填空题(共6题)
茗茗用同种材料制成的金属框架如图所示,已知 ,,,其中 的周长为 ,,则制成整个金属框架所需材料的长度为 .
把等腰直角三角形纸板 按如图所示的方式直立在桌面上,顶点 顶着桌面,若另外两个顶点与桌面的距离分别为 和 ,过另外两个顶点向桌面作垂线,则两个垂足之间的距离 为 .
利用三角形全等测距离,实际就是利用知识点“全等三角形的 相等”来解决.
如图,一块三角形玻璃碎成了Ⅰ,Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第 块玻璃碎片.
如图,有两个长度相等的滑梯 和 ,,则当 时,可以得出左边滑梯的高度 与右边滑梯水平方向的长度 相等.
在正方形 中,已知点 在边 上,,,如图所示.把线段 绕点 旋转,使点 落在直线 上的点 处,则 的长度 .
三、解答题(共5题)
如图,有一池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接到达点 ,,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长就是点 , 的距离,为什么?请结合解题过程,完成本题的证明.
证明:在 和 中,
.
.
如图,有两座相同的楼房,两人在六楼 , 上看两楼之间的空地上的一盆花 时,视线与水平方向的夹角(俯角)相等(即 ),你能判定一盆花 到两座楼的距离相等吗?为什么?
如图,,,试说明 .
如图, 为码头,, 两个灯塔与码头的距离相等,, 为海岸线,一轮船离开码头,计划沿 平分线航行,在航行途中,测得轮船与灯塔 , 的距离相等,试问轮船航行时是否偏离预定航线?为什么?
如图,在 中,点 是边 的中点,连接 并延长到点 ,使 ,连接 .
(1) 求证:;
(2) 若 的面积为 ,求 的面积.
答案
一、选择题(共9题)
1. 【答案】A
【知识点】三角形的三边关系
2. 【答案】C
【知识点】全等三角形的性质与判定、等腰直角三角形
3. 【答案】B
【解析】带 , 或 , 均只有一个角,无法确定三角形;
带 , 则只有两个角,也无法确定三角形.
带 , 可以用“角边角”确定三角形;
同样,带 , 可以用“角边角”确定三角形.
故选:B.
【知识点】全等三角形的应用
4. 【答案】D
【知识点】全等三角形的应用
5. 【答案】A
【知识点】同旁内角、内错角
6. 【答案】D
【解析】在 和 中,
.
【知识点】角边角
7. 【答案】C
【知识点】全等三角形的应用
8. 【答案】C
【知识点】角角边
9. 【答案】A
二、填空题(共6题)
10. 【答案】
【知识点】全等三角形的应用
11. 【答案】
【解析】由 得 ,因为 ,所以 ,所以 .又因为 ,,所以 .从而 ,,所以 .
【知识点】全等三角形的应用
12. 【答案】对应边
【知识点】全等三角形的应用
13. 【答案】
【知识点】全等三角形的应用
14. 【答案】
【解析】由题意得,在 和 中, .
.
又 ,
.
【知识点】斜边、直角边
15. 【答案】 或
【解析】分成两种情况,如图所示. 或 .
【知识点】旋转及其性质、正方形的性质
三、解答题(共5题)
16. 【答案】 ;;;
【知识点】全等三角形的应用
17. 【答案】一盆花 到两座楼的距离相等,即 .(提示:说明 即可)
【知识点】边角边、全等三角形的应用
18. 【答案】略.提示:利用“”说明 ,从而得出 .
【知识点】边角边
19. 【答案】没有偏离.
因为 ,,,
所以 .
所以 .
【知识点】边边边、全等三角形的应用
20. 【答案】
(1) 点 是边 的中点,
,
在 和 中,
.
(2) 在 中,点 是边 的中点,
,
,
,
.
答: 的面积为 .
【知识点】边角边、全等形的概念及性质
第四章 5.利用三角形全等测距离(预习检测卷)
一、选择题(共9题)
如图,为估计池塘岸边 , 两点间的距离,小方在池塘的一侧选取一点 ,测得 ,,, 间的距离不可能是
A. B. C. D.
把等腰直角三角形纸板 按如图所示的方式直立在桌面上,顶点 顶着桌面,若另外两个顶点与桌面的距离分别为 和 ,过另外两个顶点向桌面作垂线,则两个垂足之间的距离 为
A. B. C. D.无法确定
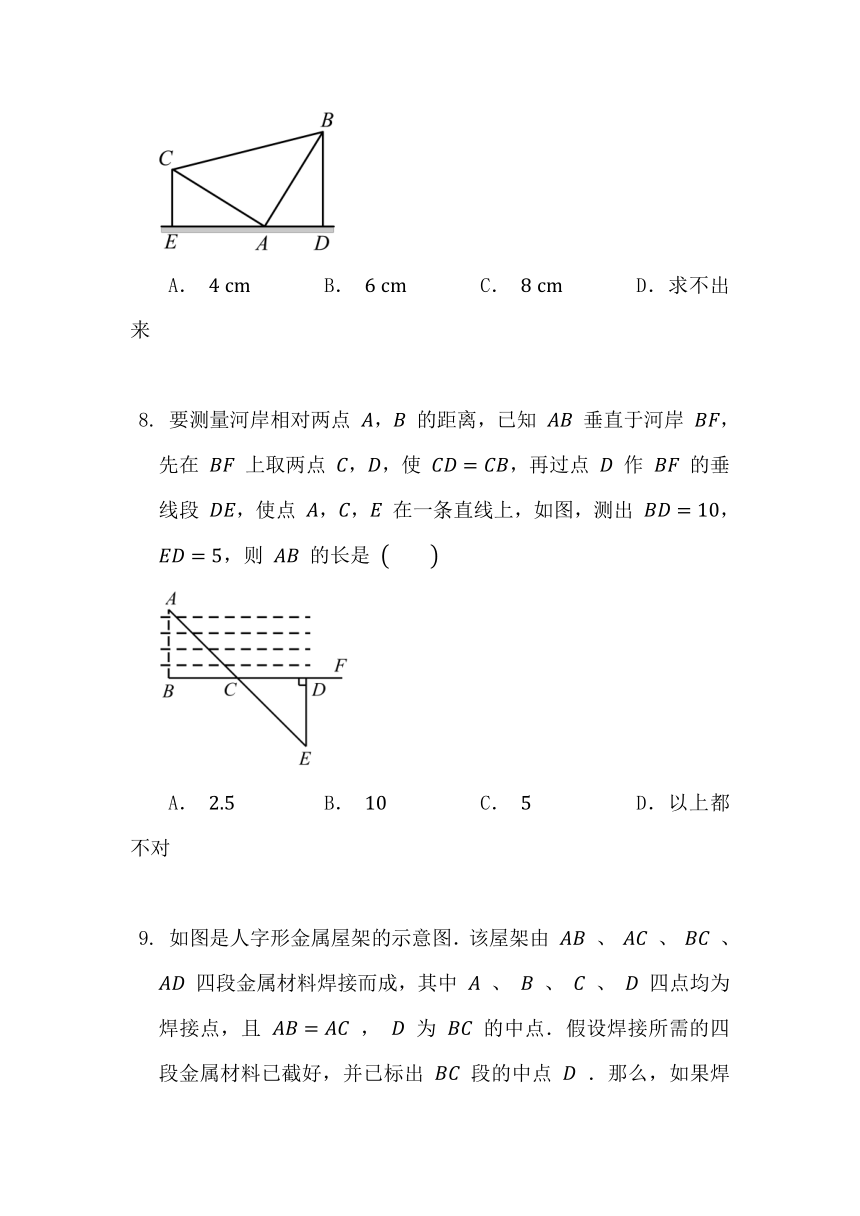
一块三角形玻璃样板不慎被张宇同学碰破了,成为四块完整碎片(如图所示),聪明的他经过仔细考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列选项中可行的是
A.带 , 或 , 去就可以了
B.带 , 或 , 去就可以了
C.带 , 或 , 去就可以了
D.带其中的任意两块去都可以
如图,为了测量点 到河对面的目标 之间的距离,在点 同侧选择了一点 ,测得 ,.然后在点 处立了标杆,使 ,,得到 ,测得 的长就是 , 两点间的距离.这里判定 的理由是
A. B. C. D.
如图,点 在 的延长线上,则下列条件中,不能判定 的是
A. B.
C. D.
如图,要测量河两岸相对的两点 , 的距离,先在 的垂线 上取两点 ,,使 ,再作出 的垂线 ,使点 ,, 在同一条直线上,可以证明 ,得到 ,因此测得 的长就是 的长,判定 最恰当的理由是
A. B. C. D.
把等腰 按如图所示立放在桌上,顶点 顶着桌面,若另两个顶点 , 距离桌面的距离分别是 和 ,垂足分别是 ,,则垂足之间的距离 的长为
A. B. C. D.求不出来
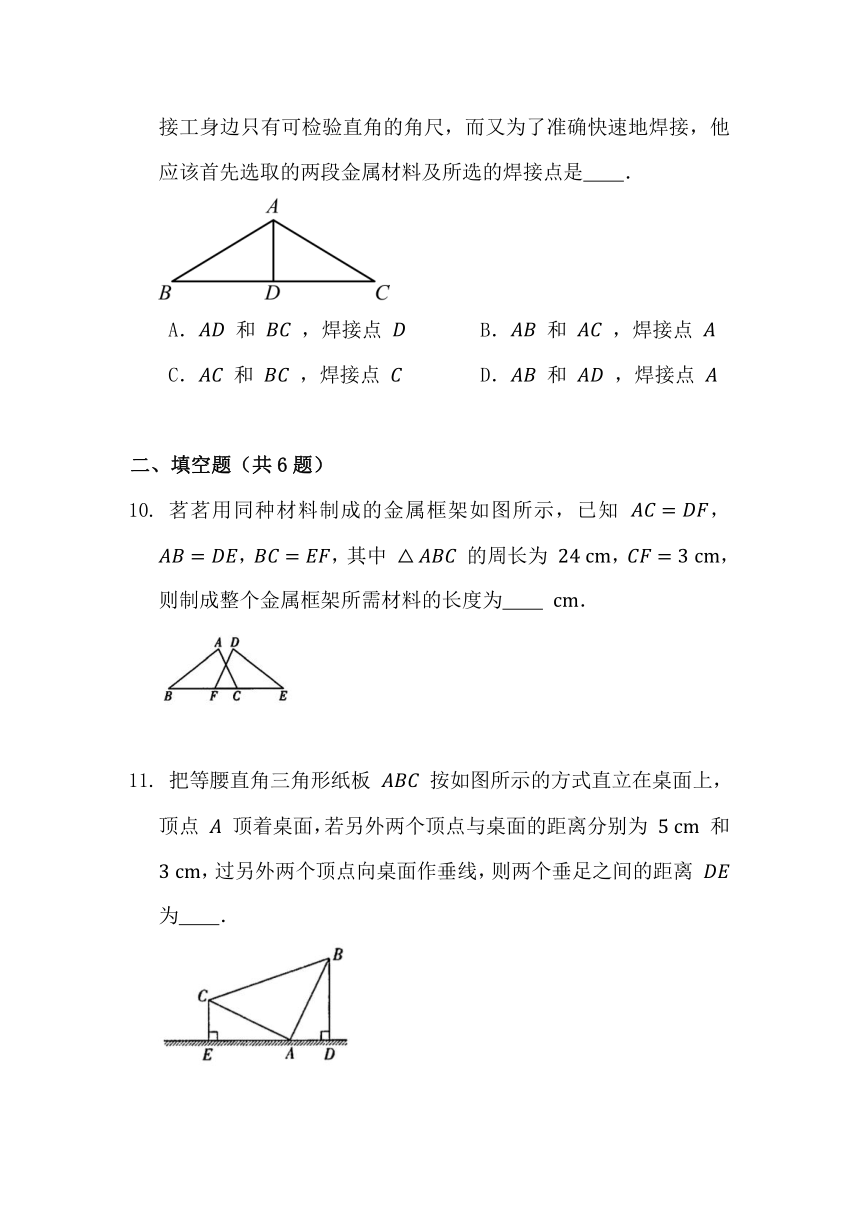
要测量河岸相对两点 , 的距离,已知 垂直于河岸 ,先在 上取两点 ,,使 ,再过点 作 的垂线段 ,使点 ,, 在一条直线上,如图,测出 ,,则 的长是
A. B. C. D.以上都不对
如图是人字形金属屋架的示意图.该屋架由 、 、 、 四段金属材料焊接而成,其中 、 、 、 四点均为焊接点,且 , 为 的中点.假设焊接所需的四段金属材料已截好,并已标出 段的中点 .那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及所选的焊接点是 .
A. 和 ,焊接点 B. 和 ,焊接点
C. 和 ,焊接点 D. 和 ,焊接点
二、填空题(共6题)
茗茗用同种材料制成的金属框架如图所示,已知 ,,,其中 的周长为 ,,则制成整个金属框架所需材料的长度为 .
把等腰直角三角形纸板 按如图所示的方式直立在桌面上,顶点 顶着桌面,若另外两个顶点与桌面的距离分别为 和 ,过另外两个顶点向桌面作垂线,则两个垂足之间的距离 为 .
利用三角形全等测距离,实际就是利用知识点“全等三角形的 相等”来解决.
如图,一块三角形玻璃碎成了Ⅰ,Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第 块玻璃碎片.
如图,有两个长度相等的滑梯 和 ,,则当 时,可以得出左边滑梯的高度 与右边滑梯水平方向的长度 相等.
在正方形 中,已知点 在边 上,,,如图所示.把线段 绕点 旋转,使点 落在直线 上的点 处,则 的长度 .
三、解答题(共5题)
如图,有一池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接到达点 ,,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长就是点 , 的距离,为什么?请结合解题过程,完成本题的证明.
证明:在 和 中,
.
.
如图,有两座相同的楼房,两人在六楼 , 上看两楼之间的空地上的一盆花 时,视线与水平方向的夹角(俯角)相等(即 ),你能判定一盆花 到两座楼的距离相等吗?为什么?
如图,,,试说明 .
如图, 为码头,, 两个灯塔与码头的距离相等,, 为海岸线,一轮船离开码头,计划沿 平分线航行,在航行途中,测得轮船与灯塔 , 的距离相等,试问轮船航行时是否偏离预定航线?为什么?
如图,在 中,点 是边 的中点,连接 并延长到点 ,使 ,连接 .
(1) 求证:;
(2) 若 的面积为 ,求 的面积.
答案
一、选择题(共9题)
1. 【答案】A
【知识点】三角形的三边关系
2. 【答案】C
【知识点】全等三角形的性质与判定、等腰直角三角形
3. 【答案】B
【解析】带 , 或 , 均只有一个角,无法确定三角形;
带 , 则只有两个角,也无法确定三角形.
带 , 可以用“角边角”确定三角形;
同样,带 , 可以用“角边角”确定三角形.
故选:B.
【知识点】全等三角形的应用
4. 【答案】D
【知识点】全等三角形的应用
5. 【答案】A
【知识点】同旁内角、内错角
6. 【答案】D
【解析】在 和 中,
.
【知识点】角边角
7. 【答案】C
【知识点】全等三角形的应用
8. 【答案】C
【知识点】角角边
9. 【答案】A
二、填空题(共6题)
10. 【答案】
【知识点】全等三角形的应用
11. 【答案】
【解析】由 得 ,因为 ,所以 ,所以 .又因为 ,,所以 .从而 ,,所以 .
【知识点】全等三角形的应用
12. 【答案】对应边
【知识点】全等三角形的应用
13. 【答案】
【知识点】全等三角形的应用
14. 【答案】
【解析】由题意得,在 和 中, .
.
又 ,
.
【知识点】斜边、直角边
15. 【答案】 或
【解析】分成两种情况,如图所示. 或 .
【知识点】旋转及其性质、正方形的性质
三、解答题(共5题)
16. 【答案】 ;;;
【知识点】全等三角形的应用
17. 【答案】一盆花 到两座楼的距离相等,即 .(提示:说明 即可)
【知识点】边角边、全等三角形的应用
18. 【答案】略.提示:利用“”说明 ,从而得出 .
【知识点】边角边
19. 【答案】没有偏离.
因为 ,,,
所以 .
所以 .
【知识点】边边边、全等三角形的应用
20. 【答案】
(1) 点 是边 的中点,
,
在 和 中,
.
(2) 在 中,点 是边 的中点,
,
,
,
.
答: 的面积为 .
【知识点】边角边、全等形的概念及性质
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
