【寒假衔接】北师大版 七年级数学下册4.3平行线的性质 预习检测卷(word版、含答案)
文档属性
| 名称 | 【寒假衔接】北师大版 七年级数学下册4.3平行线的性质 预习检测卷(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 486.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 10:54:45 | ||
图片预览

文档简介
【寒假衔接】北师大版 七年级数学下册
第二章 3.平行线的性质(预习检测卷)
一、选择题(共10题)
如图,,则根据图中标注的角,下列关系中成立的是
A. B.
C. D.
如图,直线 , 被直线 所截,且 ,则 的度数是
A. B. C. D.
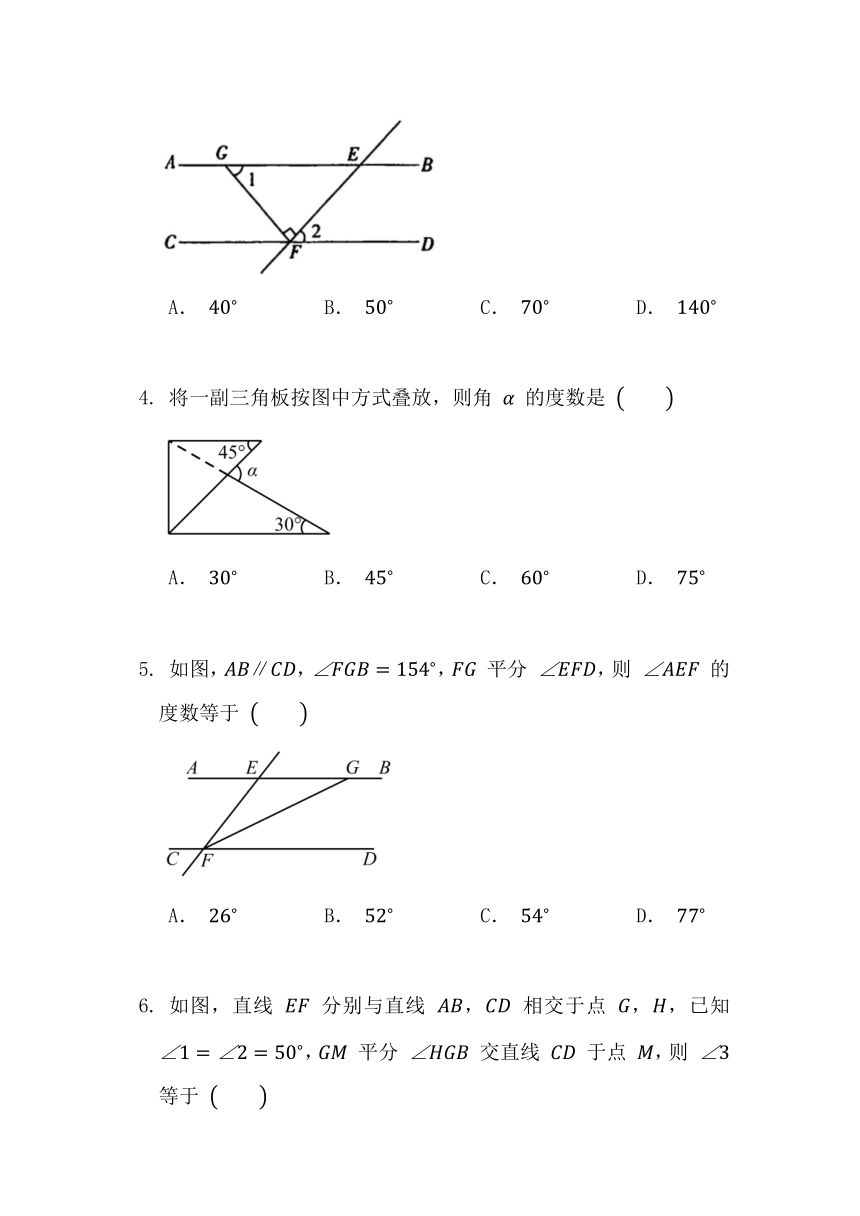
如图,, 分别交 , 于点 ,, 交 于点 ,若 ,则 的度数是
A. B. C. D.
将一副三角板按图中方式叠放,则角 的度数是
A. B. C. D.
如图,,, 平分 ,则 的度数等于
A. B. C. D.
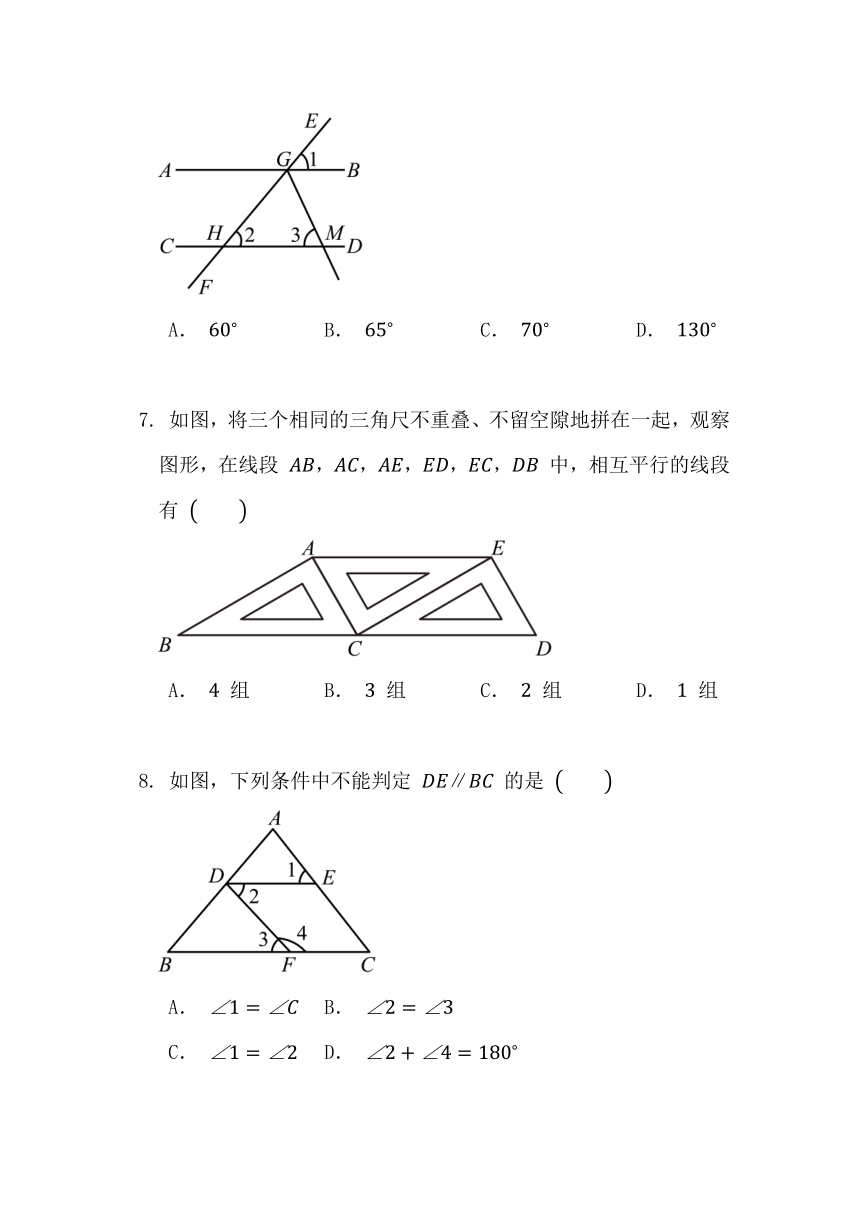
如图,直线 分别与直线 , 相交于点 ,,已知 , 平分 交直线 于点 ,则 等于
A. B. C. D.
如图,将三个相同的三角尺不重叠、不留空隙地拼在一起,观察图形,在线段 ,,,,, 中,相互平行的线段有
A. 组 B. 组 C. 组 D. 组
如图,下列条件中不能判定 的是
A. B.
C. D.
下列运算中正确的是
A. B.
C. D.
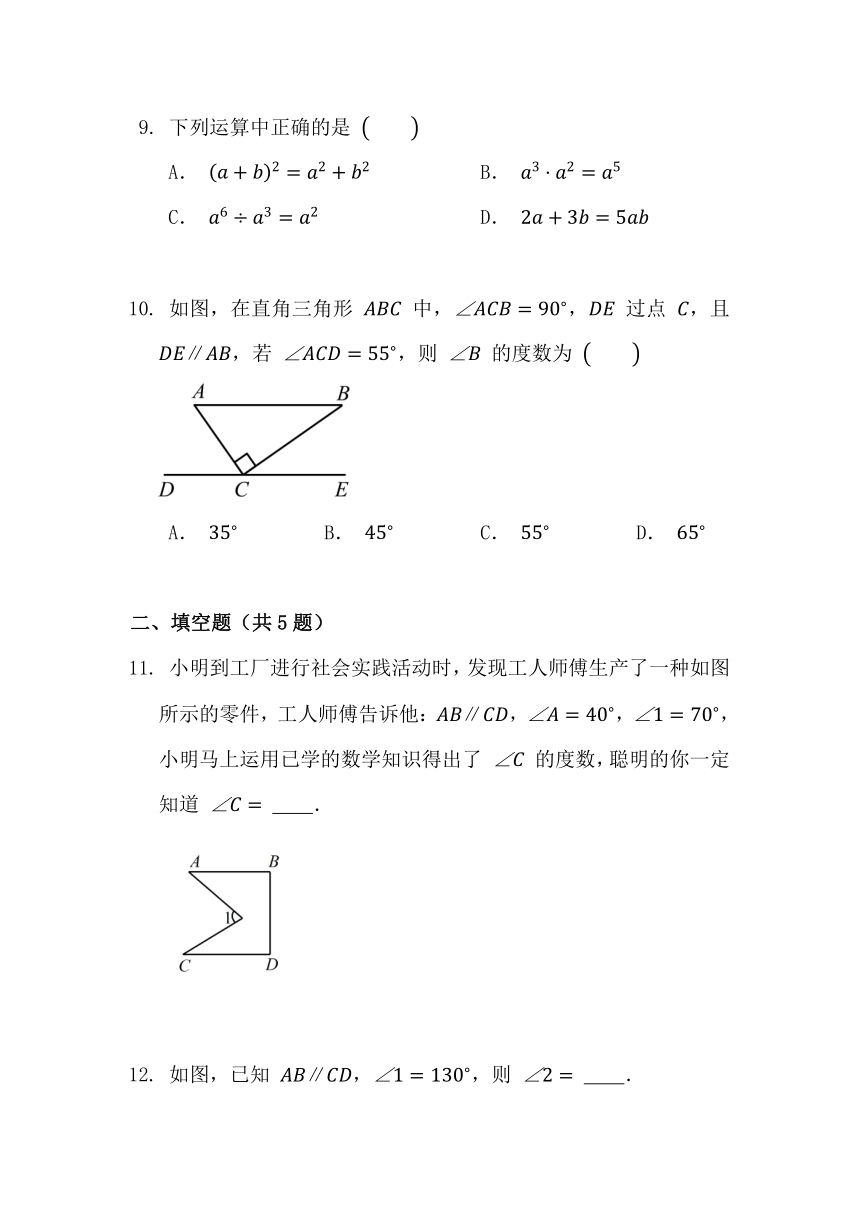
如图,在直角三角形 中,, 过点 ,且 ,若 ,则 的度数为
A. B. C. D.
二、填空题(共5题)
小明到工厂进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:,,,小明马上运用已学的数学知识得出了 的度数,聪明的你一定知道 .
如图,已知 ,,则 .
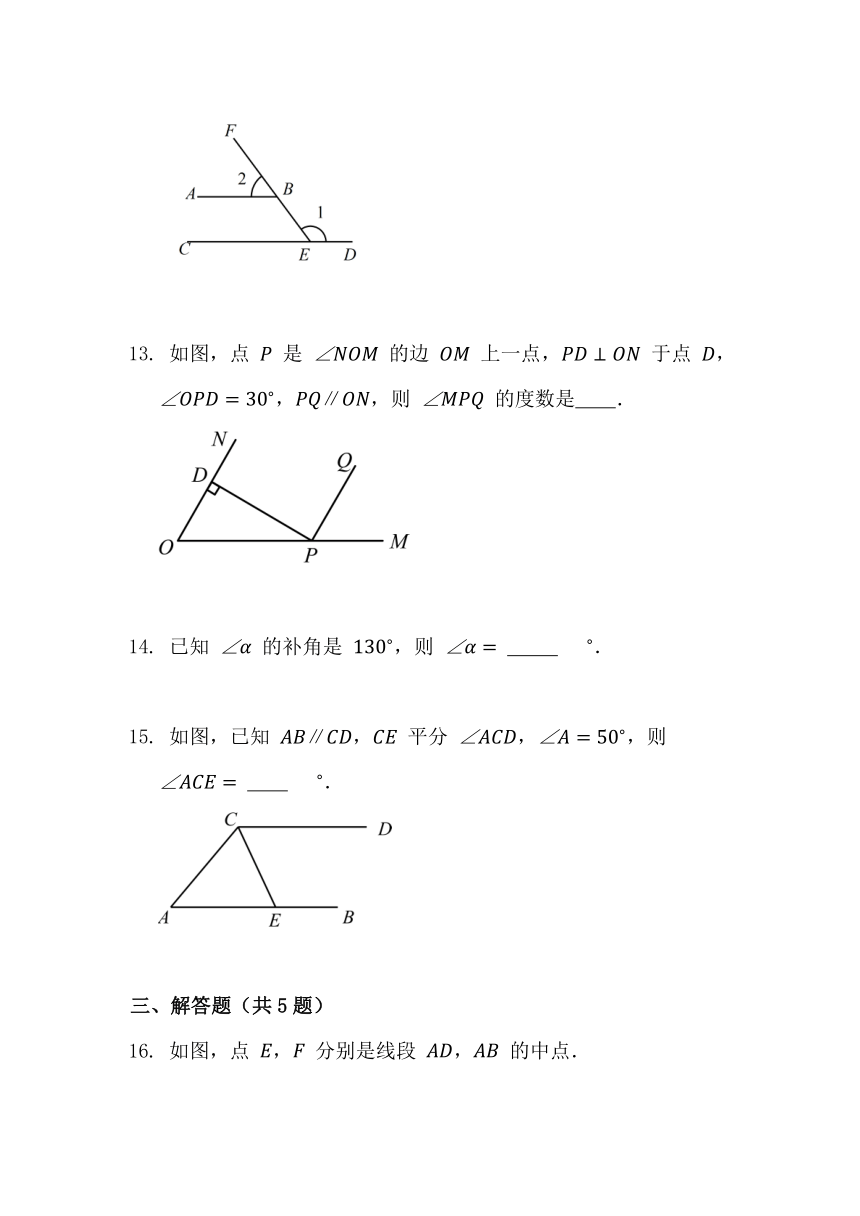
如图,点 是 的边 上一点, 于点 ,,,则 的度数是 .
已知 的补角是 ,则 .
如图,已知 , 平分 ,,则
.
三、解答题(共5题)
如图,点 , 分别是线段 , 的中点.
(1) 过点 画 ,交 于点 ;过点 画 ,交 于点 ,试判断 与 是否互相平行,并说明理由;
(2) 连接 ,,通过测量 ,,, 的度数,判断其中相等的角有哪些?互补的角有哪些?
如图,已知 以及 内一点 .
(1) 在图①中画出 ,使 的两边分别与 的两边平行,且用量角器量一下 , 的度数,可以发现:他们之间的数量关系是 ;
(2) 在图②中画出使 ,使 的两边分别与 的两边平行,且与()中的方法不同,量出 , 的度数,可以发现:它们之间的数量关系是 ;
(3) 由上述两种情况,可以得出结论:如果一个角的两边分别与另一个角的两边分别平行,则这两个角 .
在证明角相等时常见的方法有哪些?
如图,已知 , 是 平分线,,,求 和 的度数.
如图,在四边形 中,,找出图中所有与 相等的角并证明.
答案
一、选择题(共10题)
1. 【答案】D
【解析】A、 与 不平行,
不成立,故本选项错误;
B、 与 不平行,
不成立,故本选项错误;
C、 ,
,故本选项错误;
D、 ,
,故本选项正确.
【知识点】平行线的性质
2. 【答案】B
【知识点】平行线的性质
3. 【答案】A
【解析】 ,,
,
,,
.
【知识点】平行线的性质
4. 【答案】D
【知识点】内错角相等、三角形的外角及外角性质
5. 【答案】B
【解析】 ,
,
,
平分 ,
,
,
.
故选:B.
【知识点】角平分线的定义、平行线的性质
6. 【答案】B
【知识点】内错角相等、同位角
7. 【答案】B
【知识点】同位角、内错角
8. 【答案】C
【知识点】同旁内角
9. 【答案】B
【知识点】同底数幂的除法
10. 【答案】A
【知识点】内错角相等
二、填空题(共5题)
11. 【答案】
【知识点】平行线的性质、平行公理的推论
12. 【答案】
【知识点】平行线的性质、相交与垂直
13. 【答案】
【解析】 ,,
.
又 ,
.
【知识点】平行线的性质
14. 【答案】
【知识点】补角的概念
15. 【答案】
【知识点】同旁内角互补
三、解答题(共5题)
16. 【答案】
(1) 如图.
.理由:
,,
.
(2) 相等的角:,.
互补的角:,,,.
【知识点】平行线的画法、余角,补角、平行线的性质、平行公理的推论
17. 【答案】
(1) 如图①;
与 相等
(2) 如图②;
与 互补
(3) 相等或互补
【知识点】平行线的画法、角的度量、平行线的性质、余角,补角
18. 【答案】证明角相等,常见方法有:
()同角的余角相等;
()同角的补角相等;
()平行线的性质;
()等量代换等.
【知识点】余角,补角、平行线的性质
19. 【答案】 是 平分线,,
,
.
在 中,
.
,.
【知识点】平行线的性质
20. 【答案】因为 ,(已知)
所以 (两直线平行,同位角相等).
因为 ,
所以 (两直线平行,内错角相等),
所以 (等量代换).
又因为 与 时对顶角,
所以 (对顶角相等).
【知识点】平行线的性质
第二章 3.平行线的性质(预习检测卷)
一、选择题(共10题)
如图,,则根据图中标注的角,下列关系中成立的是
A. B.
C. D.
如图,直线 , 被直线 所截,且 ,则 的度数是
A. B. C. D.
如图,, 分别交 , 于点 ,, 交 于点 ,若 ,则 的度数是
A. B. C. D.
将一副三角板按图中方式叠放,则角 的度数是
A. B. C. D.
如图,,, 平分 ,则 的度数等于
A. B. C. D.
如图,直线 分别与直线 , 相交于点 ,,已知 , 平分 交直线 于点 ,则 等于
A. B. C. D.
如图,将三个相同的三角尺不重叠、不留空隙地拼在一起,观察图形,在线段 ,,,,, 中,相互平行的线段有
A. 组 B. 组 C. 组 D. 组
如图,下列条件中不能判定 的是
A. B.
C. D.
下列运算中正确的是
A. B.
C. D.
如图,在直角三角形 中,, 过点 ,且 ,若 ,则 的度数为
A. B. C. D.
二、填空题(共5题)
小明到工厂进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:,,,小明马上运用已学的数学知识得出了 的度数,聪明的你一定知道 .
如图,已知 ,,则 .
如图,点 是 的边 上一点, 于点 ,,,则 的度数是 .
已知 的补角是 ,则 .
如图,已知 , 平分 ,,则
.
三、解答题(共5题)
如图,点 , 分别是线段 , 的中点.
(1) 过点 画 ,交 于点 ;过点 画 ,交 于点 ,试判断 与 是否互相平行,并说明理由;
(2) 连接 ,,通过测量 ,,, 的度数,判断其中相等的角有哪些?互补的角有哪些?
如图,已知 以及 内一点 .
(1) 在图①中画出 ,使 的两边分别与 的两边平行,且用量角器量一下 , 的度数,可以发现:他们之间的数量关系是 ;
(2) 在图②中画出使 ,使 的两边分别与 的两边平行,且与()中的方法不同,量出 , 的度数,可以发现:它们之间的数量关系是 ;
(3) 由上述两种情况,可以得出结论:如果一个角的两边分别与另一个角的两边分别平行,则这两个角 .
在证明角相等时常见的方法有哪些?
如图,已知 , 是 平分线,,,求 和 的度数.
如图,在四边形 中,,找出图中所有与 相等的角并证明.
答案
一、选择题(共10题)
1. 【答案】D
【解析】A、 与 不平行,
不成立,故本选项错误;
B、 与 不平行,
不成立,故本选项错误;
C、 ,
,故本选项错误;
D、 ,
,故本选项正确.
【知识点】平行线的性质
2. 【答案】B
【知识点】平行线的性质
3. 【答案】A
【解析】 ,,
,
,,
.
【知识点】平行线的性质
4. 【答案】D
【知识点】内错角相等、三角形的外角及外角性质
5. 【答案】B
【解析】 ,
,
,
平分 ,
,
,
.
故选:B.
【知识点】角平分线的定义、平行线的性质
6. 【答案】B
【知识点】内错角相等、同位角
7. 【答案】B
【知识点】同位角、内错角
8. 【答案】C
【知识点】同旁内角
9. 【答案】B
【知识点】同底数幂的除法
10. 【答案】A
【知识点】内错角相等
二、填空题(共5题)
11. 【答案】
【知识点】平行线的性质、平行公理的推论
12. 【答案】
【知识点】平行线的性质、相交与垂直
13. 【答案】
【解析】 ,,
.
又 ,
.
【知识点】平行线的性质
14. 【答案】
【知识点】补角的概念
15. 【答案】
【知识点】同旁内角互补
三、解答题(共5题)
16. 【答案】
(1) 如图.
.理由:
,,
.
(2) 相等的角:,.
互补的角:,,,.
【知识点】平行线的画法、余角,补角、平行线的性质、平行公理的推论
17. 【答案】
(1) 如图①;
与 相等
(2) 如图②;
与 互补
(3) 相等或互补
【知识点】平行线的画法、角的度量、平行线的性质、余角,补角
18. 【答案】证明角相等,常见方法有:
()同角的余角相等;
()同角的补角相等;
()平行线的性质;
()等量代换等.
【知识点】余角,补角、平行线的性质
19. 【答案】 是 平分线,,
,
.
在 中,
.
,.
【知识点】平行线的性质
20. 【答案】因为 ,(已知)
所以 (两直线平行,同位角相等).
因为 ,
所以 (两直线平行,内错角相等),
所以 (等量代换).
又因为 与 时对顶角,
所以 (对顶角相等).
【知识点】平行线的性质
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
