2019人教版选择性必修第一册第四章第2节全反射提升练习(word版含答案)
文档属性
| 名称 | 2019人教版选择性必修第一册第四章第2节全反射提升练习(word版含答案) | 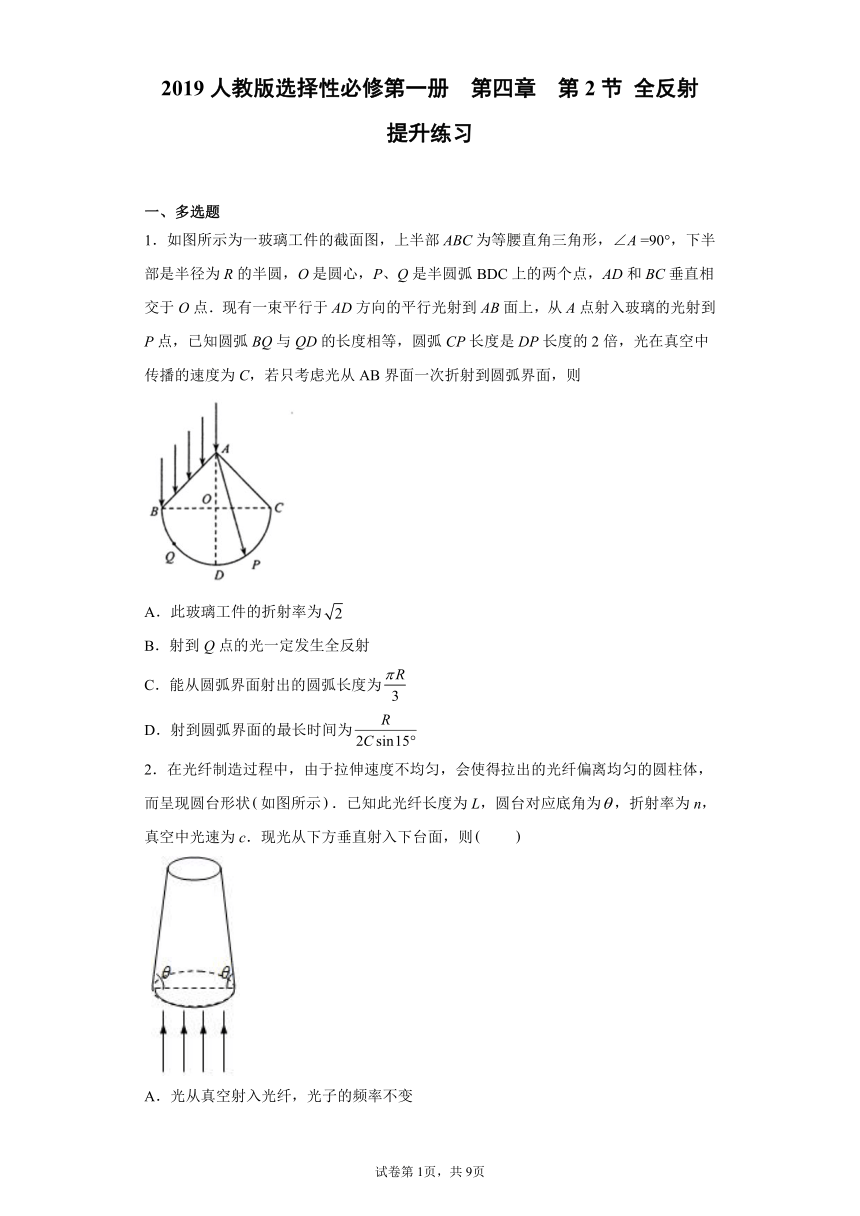 | |
| 格式 | docx | ||
| 文件大小 | 647.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-23 03:15:42 | ||
图片预览




文档简介
2019人教版选择性必修第一册 第四章 第2节 全反射 提升练习
一、多选题
1.如图所示为一玻璃工件的截面图,上半部ABC为等腰直角三角形,∠A =90°,下半部是半径为R的半圆,O是圆心,P、Q是半圆弧BDC上的两个点,AD和BC垂直相交于O点.现有一束平行于AD方向的平行光射到AB面上,从A点射入玻璃的光射到P点,已知圆弧BQ与QD的长度相等,圆弧CP长度是DP长度的2倍,光在真空中传播的速度为C,若只考虑光从AB界面一次折射到圆弧界面,则
A.此玻璃工件的折射率为
B.射到Q点的光一定发生全反射
C.能从圆弧界面射出的圆弧长度为
D.射到圆弧界面的最长时间为
2.在光纤制造过程中,由于拉伸速度不均匀,会使得拉出的光纤偏离均匀的圆柱体,而呈现圆台形状如图所示.已知此光纤长度为L,圆台对应底角为,折射率为n,真空中光速为c.现光从下方垂直射入下台面,则
A.光从真空射入光纤,光子的频率不变
B.光通过此光纤到达小截面的最短时间为
C.从上方截面射出的光束一定是平行光
D.若满足,则光在第一次到达光纤侧面时不会从光纤侧面射出
3.由透明材料制成的长方体物块放在水平面上,且长方体物块的下表面涂有水银层面。一束由两种单色光组成的细光束沿的方向斜射到长方体物块的上表面,且与上表面的夹角大小为,结果在长方体物块的上表面得到三束光线甲、乙、丙。则下列说法正确的是 。
A.甲、乙、丙中只有甲为复色光
B.光束乙的折射率大于光束丙的折射率
C.减小角,甲、乙、丙一定平行
D.如果用以上两种色光通过相同的双缝,光束丙的条纹间距小于光束乙的条纹间距
E. 两种色光在该透明材料中传播的时间一定相等
4.下列说法正确的是( )
A.光导纤维的内芯是光密介质,外套是光疏介质
B.太阳光下的油膜呈彩色,这是太阳光经薄膜干涉产生的
C.电视机遥控器发出的红外线的波长比消毒用的紫外线的波长短
D.若红光与紫光以相同的入射角从水面射向空中,则在不断增大入射角的过程中,水面上紫光比红光先消失
E.分别用红光,紫光在同一装置上做双缝干涉实验,红光的相邻两个亮条纹的中心间距小于紫光的相邻两个亮条纹的中心间距
二、单选题
5.如图所示,一束本应会聚于A点的光束,在O点放一凸透镜会聚于B点若把一个点光源置于B点,则它发出的光线
A.经凸透镜折射后成虚像于A点
B.经凸透镜折射后成虚像于A点和B点之间
C.经凸透镜折射后成实像于凸透镜左侧
D.经凸透镜折射后成为平行光
6.在一次讨论中,老师问道:“假如水中相同深度处有a、b、c三种不同颜色的单色点光源,有人在水面上方同等条件下观测发现,b在水下的像最深,c照亮水面的面积比a的大。关于这三种光在水中的性质,同学们能作出什么判断?”有同学回答如下:①c光的频率最大;②a光的传播速度最小;③b光的折射率最小;④a光的波长比b光的长。根据老师的假定,以上回答正确的是
A.①② B.②③
C.②④ D.③④
7.下列说法中正确的是( )
A.在玻璃幕墙表面镀一定厚度的金属氧化物,利用衍射现象使外面的人在白天看不到幕墙里面的情况
B.紫外线的频率与固体物质分子的固有频率接近,容易引起分子共振,产生内能
C.来回抖动带电的梳子,在空间就会形成变化的电磁场,产生电磁波
D.地面上两北斗卫星导航终端同时发出定位申请信号,在高速运行的卫星上看两信号也一定是同时发出的
8.惠更斯在研究了光的折射现象之后曾思考过一个问题:让两束折射率不同的单色光以相同的入射角从截面为半圆形的玻璃砖左端入射,不考虑光在玻璃砖中的反射,则它们在玻璃砖中运动时间关系( )
A.折射率大的光运动时间长 B.折射率小的光运动时间长
C.它们运动的时间相等 D.无法确定
9.如图所示,光线由空气透过半圆形玻璃砖,或光线由玻璃砖射入空气的光路图中,正确的是(玻璃的折射率为1.5)( )
A.图乙、丙、丁 B.图乙、丁
C.图乙、丙 D.图甲、丙
10.下列说法正确的是( )
A.汽车灯光夜间照着自行车“尾灯”,就变得十分明亮,是利用了光的折射
B.当波源与观察者相互远离时,波源的频率会减小
C.只有狭缝宽度与波长相差不多或比波长小的情况下,才发生衍射现象
D.用透明的标准样板和单色光检查工件平面的平整度,利用了光的干涉
11.如图为一圆柱中空玻璃管,管内径为R1,外径为R2,已知R2=2R1,一束光线在圆柱横截面内射向玻璃管,为保证在内壁处光不会进入中空部分,则入射角i的最小值是( )
A.30° B.45° C.60° D.75°
12.如图,一玻璃柱体的横截面为半圆形,细的单色光束从柱体的O点(半圆的圆心)射向空气,入射角,产生的反射光束1和折射光束2恰好垂直,下列说法正确的是( )
A.玻璃的折射率为
B.光线1和光线2的传播速度相同
C.光线1和光线2的传播频率相同
D.无论α增加到多大,都不可能发生全发射
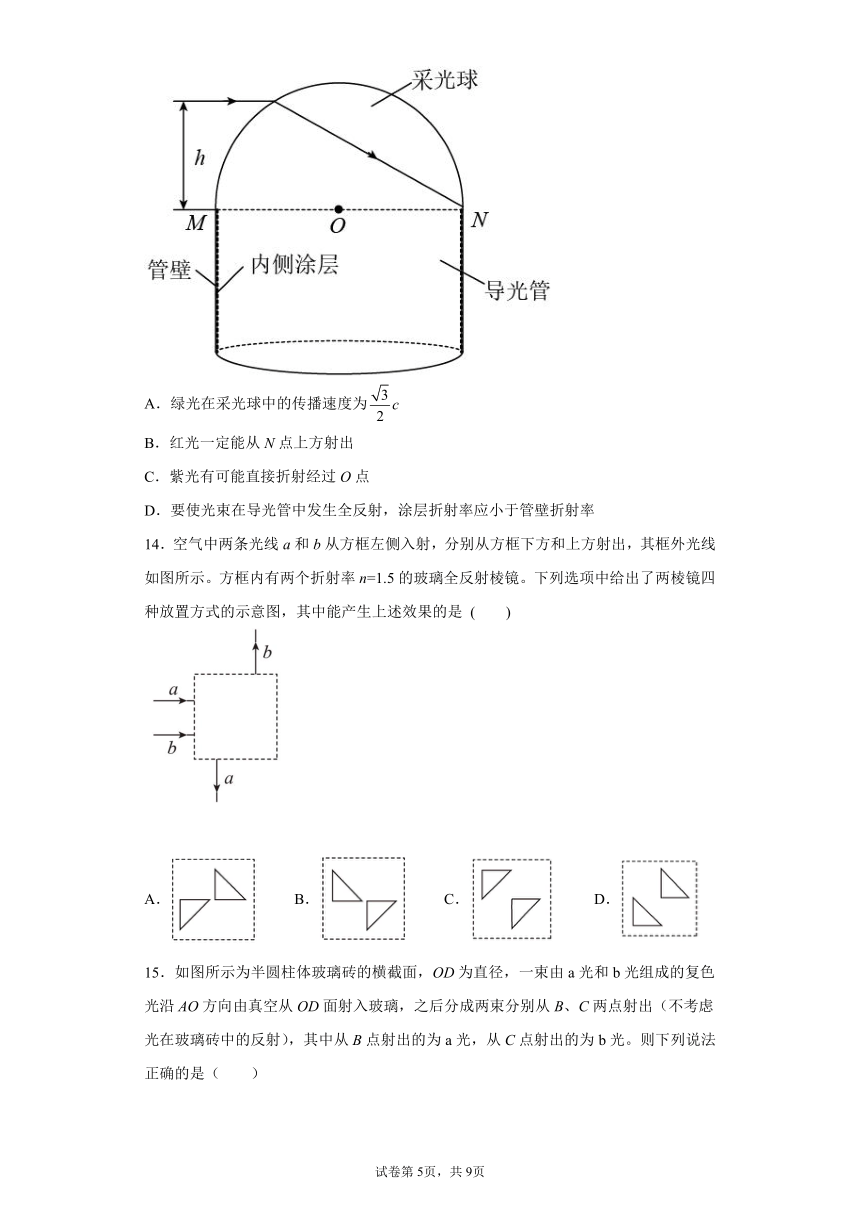
13.导光管采光系统是一套采集天然光,并经管道传输到室内的采光系统,如图为过装置中心轴线的截面。上面部分是收集阳光的半径为R的某种均匀透明材料的半球形采光球,O为球心,下面部分是内侧涂有反光涂层的导光管,MN为两部分的分界面,M、N为球面两点。若一束平行MN且与MN相距的细光束从空气入射到采光球表面时,经折射绿光恰好照射到N点。则( )
A.绿光在采光球中的传播速度为
B.红光一定能从N点上方射出
C.紫光有可能直接折射经过O点
D.要使光束在导光管中发生全反射,涂层折射率应小于管壁折射率
14.空气中两条光线a和b从方框左侧入射,分别从方框下方和上方射出,其框外光线如图所示。方框内有两个折射率n=1.5的玻璃全反射棱镜。下列选项中给出了两棱镜四种放置方式的示意图,其中能产生上述效果的是 ( )
A. B. C. D.
15.如图所示为半圆柱体玻璃砖的横截面,OD为直径,一束由a光和b光组成的复色光沿AO方向由真空从OD面射入玻璃,之后分成两束分别从B、C两点射出(不考虑光在玻璃砖中的反射),其中从B点射出的为a光,从C点射出的为b光。则下列说法正确的是( )
A.从B点射出玻璃砖的a光的频率较小
B.将a光和b光通过相同的双缝干涉装置,b光的干涉条纹间距较小
C.a光和b光在玻璃砖中的传播时间相等
D.若将a光和b光分别放在水面足够大的池塘底部同一位置,则a光照亮的水面区域大
16.如图所示,EOFGC为某种透明介质的截面图,EC是半径为R的四分之一圆弧,OFGC是一个正方形AB为足够大的水平屏幕并紧贴介质的底面,由红光和紫光两种单色光组成的复色光射向圆心O,该介质对红光和紫光的折射率分别为,设光在真空中的速度为c,则
A.红光在介质中的传播速度为
B.随着角度逐渐变大的过程中,紫光和红光依次发生全反射
C.当时,光在屏幕AF上出现了两个亮斑,则这两个亮斑之间的距离为
D.红光在玻璃中的频率比空气中的频率大
17.有一束单色光从A穿过B再折向C,如图所示,下列说法中正确的是( )
A.介质B的折射率最大 B.介质C的折射率最大
C.光在介质B中的速度最小 D.光在介质C中的速度最大
三、解答题
18.某种透明光学元件截面如图所示,区域Ⅰ为半径为R的半球形,区域Ⅱ为圆柱体,其半径也是R,BC长度也为R,且圆柱体下表面涂有反光涂层。O为AB中点,半圆形透明物质Ⅰ的折射率为,透明物质Ⅱ的折射率为。一束单色光在纸面对准O点射入半圆形透明物质Ⅰ,当逐渐减小光线与AB面垂线的夹角至θ时,通过观察发现此时从BC面射出的光线恰好在B点消失,不考虑元件中多次反射的情况。求:
(1)透明物质Ⅱ的折射率;
(2)光线与AB面垂线的夹角θ的正弦值。
19.如图所示,平面镜M斜放入装满水的槽中,一束单色光从O点以入射角α射入水中,经水面折射和平面镜反射后从O点右侧水面上某点回到空气中,最后射到槽右侧上方的屏幕N上形成一个光点。改变平面镜M与水平面夹角θ,当θ=450时,屏幕上的光点恰好消失。已知水对该单色光的折射率为,所有光线均在同一竖直平面内,求入射角α。
20.如图所示为某玻璃砖的截面图,ABCE部分为梯形,AB垂直于上、下两底.CD是ED圆弧所在圆的直径,O为圆心,直径CD长为d,∠ECO=60 ,一束单色光从AB的中点斜射入玻璃砖,在AE面上刚好发生全反射,经AE面反射后反射光刚好垂直平分CE,求:
①光在AB面的入射角的正弦值及玻璃对单色光的折射率;
②光在玻璃砖中运动的时间.(已知光在真空中的传播速度为c)
21.如图,半径为R的玻璃球冠,其底面AB镀银,底面的半径是球半径的倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线(该光线的延长线恰好过底面边缘上的A点)射到球冠上的M点经球冠折射后到达底面AB上的E点(图中未标出),再经E点反射后反射光线通过球心,最后从球冠上的F点(图中未标出)射出,已知光速为c,求:
(1)玻璃球冠的折射率;
(2)光线从M点传到F点的时间。
22.如图所示,在平静的湖面岸边处,垂钓者的眼晴恰好位于岸边P点正上方0.9 m高度处,浮标Q离P点1.2 m远,鱼饵灯M在浮标正前方1.8 m远处的水下,垂钓者发现鱼饵灯刚好被浮标挡住,已知水的折射率
① 求鱼饵灯离水面的深度
② 若鱼饵灯缓慢竖直上浮,当它离水面深多少时,鱼饵灯发出的光恰好无法从水面PQ间射出。
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.ABC
【详解】
A.如图所示:
过A点做AB面的法线,连接AP,连接OP,设从A点射入玻璃的光的入射角为i,折射角为r,则i=45°,设OP与OD夹角为θ1,由于圆弧CP长度是DP的2倍,则,设AP与AD夹角为θ2,由于△ABC为等腰直角三角形,则OA=OP=R,所以△AOP是等腰三角形,,r=∠OAC-θ2=30°,由折射定律有:,解得:
故A正确.
B.设玻璃的临界角为C,,解得:
C=45°
作出射到圆弧上Q点光线FQ,连接OQ,设FQ与BC的夹角为θ3,FQ与OQ的夹角θ4,因为圆弧BQ与QD的长度相等,所以∠BOQ=45°,因为所有入射光平行,所以所有折射光线平行,则θ3=90°-θ2=75° ,θ4=180°-θ3-∠BOQ=60°,由于θ4>C,所以射到Q点的光一定发生全反射.故B正确.
C.由上可知对应的圆心角是60°,可得圆能从圆弧界面射出的圆弧长度为.故C正确.
D.当光线沿AP射出时,所用时间最长,根据几何关系可得:,速度为:,传播的时间为:
故D错误.
2.AD
【详解】
A、光子的频率由光源决定,与介质无关,所以光从真空射入光纤,光子的频率不变;故A正确.
B、光通过此光纤到达小截面的最短距离为L,光在光纤中的传播速度,则光通过此光纤到达小截面的最短时间为;故B错误.
C、通过光纤侧面全反射后再从上方截面射出的光束与垂直射出上方截面的光束不平行;故C错误.
D、设临界角为C,则到达光纤侧面光线入射角等于,当,即有,则光在第一次到达光纤侧面时发生全反射,不会从光纤侧面射出;故D正确.
故选AD.
【点睛】
解决本题的关键是掌握全反射现象的条件和临界角公式,结合几何知识进行分析.要注意光的频率与介质无关,而光速与介质有关.
3.ABC
【解析】
【详解】
所有色光都能反射,则由反射定律可知,不同色光的反射角均相同,因此甲光束仍为复色光,而乙光束、丙光束由于折射率不同导致偏折分离,因此为单色光,A正确;由图知,光束乙的偏折程度大于光束丙,根据折射定律可知光束乙的折射率大于光束丙的折射率,B正确;一束由两种色光混合的复色光沿AO方向射出,经过折射、反射、再折射后,光线仍是平行,因为第一次折射时的折射角与第二次折射时的入射角是相等的,反射时反射角与入射角相等,所以由光路可逆可得出射光线平行。如果减小角,光束甲、乙、丙仍保持平行,C正确;光束乙的折射率大于光束丙,则光束乙的频率大于光束丙,光束乙的波长小于光束丙的波长,而双缝干涉条纹间距与波长成正比,则双缝干涉实验中光束乙产生的条纹间距比光束丙小,D错误;根据,则光在玻璃中的传播时间,因两光束的折射角r不同,所以在该透明材料中传播的时间t不相等,E错误。
4.ABD
【详解】
A.光导纤维有内、外两层材料,其中内层是光密介质,外层是光疏介质,故A正确;
B.在太阳光照射下,水面上油膜前后表面反射光,频率相同,出现彩色是因为光的薄膜干涉现象,故B正确;
C.根据电磁波谱的特点可知,红外线的波长比紫外线的波长要长,故C错误;
D.根据
可知,紫光的频率大,临界角小,在不断增大入射角的过程中,水面上紫光比红光先消失,故D正确;
E.红光的波长长于紫光波长,根据
可知在同一装置上做双缝干涉实验,红光的相邻两个亮条纹的中心间距大于紫光的相邻两个亮条纹的中心间距,故E错误。
故选ABD。
5.A
【解析】
【详解】
凸透镜成像是折射成像,根据光路的可逆性可知,把一个点光源置于B点,发出两条光线沿着原光线返回,折射光线依然沿着原来的光路,故经凸透镜折射后反向延长线在A点,故成虚像于A点,故A正确,B,C,D错误;故选A.
【点睛】
本题关键明确凸透镜成像是折射成像,折射成像光路是可逆的.
6.B
【详解】
由视深与实深的关系式 可知b光的折射率最小,故③正确;c光从水下照亮水面的面积比a的大说明c光不容易发生全反射,即c光的折射率比a光的小,其频率也小于a的频率,故①错误,综上可知nb7.C
【详解】
A.在玻璃幕墙表面镀一定厚度的金属氧化物,利用镜面反射使外面的人看不到幕墙里面的情况,A错误;
B.红外线的频率与固体物质分子的固有频率接近,容易引起分子共振,产生内能,B错误;
C.来回抖动带电的梳子,产生变化的电场,变化的电场产生变化的磁场,变化的电场和变化的磁场交替产生,形成电磁波,C正确;
D.地面上两北斗卫星导航终端同时发出定位申请信号,在高速运行的卫星上看两信号不是同时的,D错误。
故选C。
8.C
【详解】
设光的入射角为,折射角为,则根据折射定律有
又因为
设圆的直径为,则光在玻璃砖中的运动的距离为,光在玻璃砖中运动的时间为
将以上式子联立后求得
由于两种单色光的入射角相等,所以它们在玻璃砖中运动的时间相同。
故选C。
9.B
【详解】
光线由空气进入玻璃砖中时,入射角大于折射角,由玻璃砖射入空气时,入射角小于折射角,由临界角计算公式得
入射角50°大于临界角,将发生全反射。
ACD错误,B正确。
故选B。
10.D
【详解】
A.自行车“尾灯”为全反射棱镜,利用光的全反射现象,故A错误;
B.当波源与观察者相互远离时,根据多普勒效应,可知观察者接收到的频率减小,但是波源的频率不变,故B错误;
C.只有狭缝宽度与波长相差不多或比波长小的情况下,才发生明显衍射现象,故C错误;
D.用透明的标准样板和单色光检查工件平面的平整度,利用了光的薄膜干涉现象。故D正确。
故选D。
11.A
【详解】
光路图如图,设第一次折射角为r,全反射临界角为C,折射率为n。由折射定律有 ,得: ,又
对图中△ABO,由正弦定理得:,则得: 可解得i=30°,所以为保证在内壁处光不会进入中空部分,入射角i应满足i≥30°,故选A。
点睛:本题考查了光的折射、全反射的知识,解题时要正确画出光路图,找到恰好发生全反射的临界光线;能正确充分利用数学知识是解决此类问题的关键。
12.C
【详解】
A.反射光束1和折射光束2恰好垂直,由几何知识可求得此时的折射角为,由折射定律可得,玻璃的折射率为
可求得:,故A错误;
B.同一单色光,在不同介质中传播时,速度不同,但频率相同,故B错误,C正确;
D.光从光密介质进入光疏介质,当入射角等于或大于临界角时,将发生全反射现象,根据公式
由题可求得该单色光从玻璃进入空气时的临界角
到范围内有该值存在,所以当时,将发生全反射,故D错误。
故选C。
13.B
【详解】
A.如图所示
根据几何关系
,
折射率
绿光在采光球中的传播速度为
故A错误;
B.红光折射率小,折射角大,则红光一定能从N点上方射出,故B正确;
C.紫光不可能直接折射经过O点,如果过的话,折射角为0°,故C错误;
D.光由光密到光疏可能发生全反射,则涂层折射率应大于管壁折射率,故D错误。
故选B。
14.B
【详解】
玻璃折射率为,由临界角公式得
可得出玻璃砖的临界角,则当光线垂直直角边进入玻璃砖,射到斜边上时入射角为45°,光线能发生全反射,故可知B图可产生如图所示的效果,故选B。
15.C
【详解】
A.由图可知,玻璃砖对a光的折射率大于b光的折射率,所以a光的频率较大,A错误;
B.,由干涉条纹间距公式
可知b光的干涉条纹间距较大,B错误;
C.连接B、D;C、D,设,,设玻璃砖半径为R,则有
,
设玻璃砖对a光的折射率为,对b光的折射率为,则有
,
故a光和b光在玻璃砖的传播时间为
,
设复色光从真空射入玻璃砖时的入射角为,则有
,
联立以上各式解得
C正确;
D.a光和b光在水中传播时有
由
可知b光的全反射临界角较大,所以b光照亮的范围大,D错误。
故选C。
16.C
【详解】
A.红光在介质中传播的速度
选项A错误;
B.α不是入射角,由可知,红光的全反射角为60° ,紫光的全反射角为45°,所以当α逐渐变大的过程中,入射角逐渐变小,红光和紫光均不会发生全反射,B错误;
C.当α=53°时,对应的入射角:i=37°,光在屏幕AF上出现了两个亮斑分别是红色光与紫色光的紫色光,所以在AM区域的亮斑P1为红色,在AN区域的亮斑P2为红色与紫色的混合色.画出如图光路图.
设折射角分别为r1和r2,两个光斑分别为P1、P2,根据折射定律:
得:
,
由几何知识可得:
解得:
同理解得:
所以:
故C正确;
D.同一单色光在不同的介质中传播时频率不变,D错误.
17.B
【详解】
AB.由光路的可逆性,假设光分别由B进入A和C,根据折射率的物理意义可知,折射率是反映介质对光线偏折程度的物理量,进入C的偏折程度大于进入A的偏折程度,可知C的折射率比A的大,B中的入射角最大,折射率最小,可得
nC>nA>nB
A错误,B正确;
CD.由可以判断出,光在B中传播的速度最大,在C中传播的速度最小,CD错误。
故选B。
18.(1);(2)
【详解】
(1)由题意可知,光线与AB面垂线的夹角为θ时,射向BC面的光线恰好发生全反射,光路图如图所示
设透明物质Ⅱ的临界角为C,由几何关系可知
解得
(2)由光的折射定律可得
由几何关系可得
联立解得
19.600
【解析】试题分析:先画出光路图,屏幕上的光点恰好消失时,入射角等于临界角,由几何关系和全反射临界角公式求折射率n,再由折射定律求得入射角。
画出如图所示的光路图所示:
设入射为α,OA是入射到平面镜上的光线,AD是法线,设, ,由几何关系得:
由折射定律得:
因为:
代入解得:
可得:α=600
试题分析:本题主要考查了折射和反射两种光学现象,根据折射定律和反射定律进行分析.对于平面镜,要充分利用对称性分析光路。
20.(1)(2)
【解析】
由题意可知,CE是圆的一个弦.因此经AE面反射后反射光垂直平分CE,则反射光刚好照射到圆心O,光路图如图所示.
由几何关系可知,光钱在AE面的入射角为60 ,由于光线刚好在AE面上发生全反射,则全反射的临界角:C=60
则玻璃对光的折射率:
由几何关系可知,光在AB面上折射的折射角为r=30 ,设入射角为i,则
求得:
②由几何关系,圆弧的直径为d,则AB长为
则光在玻璃种传播的距离
光在玻璃种传播的时间
点睛:本题的关键是要掌握有关折射率的两个公式和.解题时,要作出光路图,利用几何知识帮助解答.
21.(1);(2)
【详解】
(1)光路图如图所示
根据几何关系得
解得,故,所以为等边三角形
又
解得
所以
由折射定律得
解得
(2)由几何关系可得,该光线在球冠中的传播路程
可知光在球冠中的传播时间
联立解得
22.① ②
【详解】
①设入射角、折射角分别为、,鱼饵灯离水面深度为,作出光路如图
则有
,
据光的折射定律,解得
②当鱼饵灯离水面深度为时,水面PQ间恰无光射出,此时鱼饵灯与浮标的连线和竖直方向的夹角恰好为临界角C,则
解得
答案第1页,共2页
答案第1页,共2页
一、多选题
1.如图所示为一玻璃工件的截面图,上半部ABC为等腰直角三角形,∠A =90°,下半部是半径为R的半圆,O是圆心,P、Q是半圆弧BDC上的两个点,AD和BC垂直相交于O点.现有一束平行于AD方向的平行光射到AB面上,从A点射入玻璃的光射到P点,已知圆弧BQ与QD的长度相等,圆弧CP长度是DP长度的2倍,光在真空中传播的速度为C,若只考虑光从AB界面一次折射到圆弧界面,则
A.此玻璃工件的折射率为
B.射到Q点的光一定发生全反射
C.能从圆弧界面射出的圆弧长度为
D.射到圆弧界面的最长时间为
2.在光纤制造过程中,由于拉伸速度不均匀,会使得拉出的光纤偏离均匀的圆柱体,而呈现圆台形状如图所示.已知此光纤长度为L,圆台对应底角为,折射率为n,真空中光速为c.现光从下方垂直射入下台面,则
A.光从真空射入光纤,光子的频率不变
B.光通过此光纤到达小截面的最短时间为
C.从上方截面射出的光束一定是平行光
D.若满足,则光在第一次到达光纤侧面时不会从光纤侧面射出
3.由透明材料制成的长方体物块放在水平面上,且长方体物块的下表面涂有水银层面。一束由两种单色光组成的细光束沿的方向斜射到长方体物块的上表面,且与上表面的夹角大小为,结果在长方体物块的上表面得到三束光线甲、乙、丙。则下列说法正确的是 。
A.甲、乙、丙中只有甲为复色光
B.光束乙的折射率大于光束丙的折射率
C.减小角,甲、乙、丙一定平行
D.如果用以上两种色光通过相同的双缝,光束丙的条纹间距小于光束乙的条纹间距
E. 两种色光在该透明材料中传播的时间一定相等
4.下列说法正确的是( )
A.光导纤维的内芯是光密介质,外套是光疏介质
B.太阳光下的油膜呈彩色,这是太阳光经薄膜干涉产生的
C.电视机遥控器发出的红外线的波长比消毒用的紫外线的波长短
D.若红光与紫光以相同的入射角从水面射向空中,则在不断增大入射角的过程中,水面上紫光比红光先消失
E.分别用红光,紫光在同一装置上做双缝干涉实验,红光的相邻两个亮条纹的中心间距小于紫光的相邻两个亮条纹的中心间距
二、单选题
5.如图所示,一束本应会聚于A点的光束,在O点放一凸透镜会聚于B点若把一个点光源置于B点,则它发出的光线
A.经凸透镜折射后成虚像于A点
B.经凸透镜折射后成虚像于A点和B点之间
C.经凸透镜折射后成实像于凸透镜左侧
D.经凸透镜折射后成为平行光
6.在一次讨论中,老师问道:“假如水中相同深度处有a、b、c三种不同颜色的单色点光源,有人在水面上方同等条件下观测发现,b在水下的像最深,c照亮水面的面积比a的大。关于这三种光在水中的性质,同学们能作出什么判断?”有同学回答如下:①c光的频率最大;②a光的传播速度最小;③b光的折射率最小;④a光的波长比b光的长。根据老师的假定,以上回答正确的是
A.①② B.②③
C.②④ D.③④
7.下列说法中正确的是( )
A.在玻璃幕墙表面镀一定厚度的金属氧化物,利用衍射现象使外面的人在白天看不到幕墙里面的情况
B.紫外线的频率与固体物质分子的固有频率接近,容易引起分子共振,产生内能
C.来回抖动带电的梳子,在空间就会形成变化的电磁场,产生电磁波
D.地面上两北斗卫星导航终端同时发出定位申请信号,在高速运行的卫星上看两信号也一定是同时发出的
8.惠更斯在研究了光的折射现象之后曾思考过一个问题:让两束折射率不同的单色光以相同的入射角从截面为半圆形的玻璃砖左端入射,不考虑光在玻璃砖中的反射,则它们在玻璃砖中运动时间关系( )
A.折射率大的光运动时间长 B.折射率小的光运动时间长
C.它们运动的时间相等 D.无法确定
9.如图所示,光线由空气透过半圆形玻璃砖,或光线由玻璃砖射入空气的光路图中,正确的是(玻璃的折射率为1.5)( )
A.图乙、丙、丁 B.图乙、丁
C.图乙、丙 D.图甲、丙
10.下列说法正确的是( )
A.汽车灯光夜间照着自行车“尾灯”,就变得十分明亮,是利用了光的折射
B.当波源与观察者相互远离时,波源的频率会减小
C.只有狭缝宽度与波长相差不多或比波长小的情况下,才发生衍射现象
D.用透明的标准样板和单色光检查工件平面的平整度,利用了光的干涉
11.如图为一圆柱中空玻璃管,管内径为R1,外径为R2,已知R2=2R1,一束光线在圆柱横截面内射向玻璃管,为保证在内壁处光不会进入中空部分,则入射角i的最小值是( )
A.30° B.45° C.60° D.75°
12.如图,一玻璃柱体的横截面为半圆形,细的单色光束从柱体的O点(半圆的圆心)射向空气,入射角,产生的反射光束1和折射光束2恰好垂直,下列说法正确的是( )
A.玻璃的折射率为
B.光线1和光线2的传播速度相同
C.光线1和光线2的传播频率相同
D.无论α增加到多大,都不可能发生全发射
13.导光管采光系统是一套采集天然光,并经管道传输到室内的采光系统,如图为过装置中心轴线的截面。上面部分是收集阳光的半径为R的某种均匀透明材料的半球形采光球,O为球心,下面部分是内侧涂有反光涂层的导光管,MN为两部分的分界面,M、N为球面两点。若一束平行MN且与MN相距的细光束从空气入射到采光球表面时,经折射绿光恰好照射到N点。则( )
A.绿光在采光球中的传播速度为
B.红光一定能从N点上方射出
C.紫光有可能直接折射经过O点
D.要使光束在导光管中发生全反射,涂层折射率应小于管壁折射率
14.空气中两条光线a和b从方框左侧入射,分别从方框下方和上方射出,其框外光线如图所示。方框内有两个折射率n=1.5的玻璃全反射棱镜。下列选项中给出了两棱镜四种放置方式的示意图,其中能产生上述效果的是 ( )
A. B. C. D.
15.如图所示为半圆柱体玻璃砖的横截面,OD为直径,一束由a光和b光组成的复色光沿AO方向由真空从OD面射入玻璃,之后分成两束分别从B、C两点射出(不考虑光在玻璃砖中的反射),其中从B点射出的为a光,从C点射出的为b光。则下列说法正确的是( )
A.从B点射出玻璃砖的a光的频率较小
B.将a光和b光通过相同的双缝干涉装置,b光的干涉条纹间距较小
C.a光和b光在玻璃砖中的传播时间相等
D.若将a光和b光分别放在水面足够大的池塘底部同一位置,则a光照亮的水面区域大
16.如图所示,EOFGC为某种透明介质的截面图,EC是半径为R的四分之一圆弧,OFGC是一个正方形AB为足够大的水平屏幕并紧贴介质的底面,由红光和紫光两种单色光组成的复色光射向圆心O,该介质对红光和紫光的折射率分别为,设光在真空中的速度为c,则
A.红光在介质中的传播速度为
B.随着角度逐渐变大的过程中,紫光和红光依次发生全反射
C.当时,光在屏幕AF上出现了两个亮斑,则这两个亮斑之间的距离为
D.红光在玻璃中的频率比空气中的频率大
17.有一束单色光从A穿过B再折向C,如图所示,下列说法中正确的是( )
A.介质B的折射率最大 B.介质C的折射率最大
C.光在介质B中的速度最小 D.光在介质C中的速度最大
三、解答题
18.某种透明光学元件截面如图所示,区域Ⅰ为半径为R的半球形,区域Ⅱ为圆柱体,其半径也是R,BC长度也为R,且圆柱体下表面涂有反光涂层。O为AB中点,半圆形透明物质Ⅰ的折射率为,透明物质Ⅱ的折射率为。一束单色光在纸面对准O点射入半圆形透明物质Ⅰ,当逐渐减小光线与AB面垂线的夹角至θ时,通过观察发现此时从BC面射出的光线恰好在B点消失,不考虑元件中多次反射的情况。求:
(1)透明物质Ⅱ的折射率;
(2)光线与AB面垂线的夹角θ的正弦值。
19.如图所示,平面镜M斜放入装满水的槽中,一束单色光从O点以入射角α射入水中,经水面折射和平面镜反射后从O点右侧水面上某点回到空气中,最后射到槽右侧上方的屏幕N上形成一个光点。改变平面镜M与水平面夹角θ,当θ=450时,屏幕上的光点恰好消失。已知水对该单色光的折射率为,所有光线均在同一竖直平面内,求入射角α。
20.如图所示为某玻璃砖的截面图,ABCE部分为梯形,AB垂直于上、下两底.CD是ED圆弧所在圆的直径,O为圆心,直径CD长为d,∠ECO=60 ,一束单色光从AB的中点斜射入玻璃砖,在AE面上刚好发生全反射,经AE面反射后反射光刚好垂直平分CE,求:
①光在AB面的入射角的正弦值及玻璃对单色光的折射率;
②光在玻璃砖中运动的时间.(已知光在真空中的传播速度为c)
21.如图,半径为R的玻璃球冠,其底面AB镀银,底面的半径是球半径的倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线(该光线的延长线恰好过底面边缘上的A点)射到球冠上的M点经球冠折射后到达底面AB上的E点(图中未标出),再经E点反射后反射光线通过球心,最后从球冠上的F点(图中未标出)射出,已知光速为c,求:
(1)玻璃球冠的折射率;
(2)光线从M点传到F点的时间。
22.如图所示,在平静的湖面岸边处,垂钓者的眼晴恰好位于岸边P点正上方0.9 m高度处,浮标Q离P点1.2 m远,鱼饵灯M在浮标正前方1.8 m远处的水下,垂钓者发现鱼饵灯刚好被浮标挡住,已知水的折射率
① 求鱼饵灯离水面的深度
② 若鱼饵灯缓慢竖直上浮,当它离水面深多少时,鱼饵灯发出的光恰好无法从水面PQ间射出。
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.ABC
【详解】
A.如图所示:
过A点做AB面的法线,连接AP,连接OP,设从A点射入玻璃的光的入射角为i,折射角为r,则i=45°,设OP与OD夹角为θ1,由于圆弧CP长度是DP的2倍,则,设AP与AD夹角为θ2,由于△ABC为等腰直角三角形,则OA=OP=R,所以△AOP是等腰三角形,,r=∠OAC-θ2=30°,由折射定律有:,解得:
故A正确.
B.设玻璃的临界角为C,,解得:
C=45°
作出射到圆弧上Q点光线FQ,连接OQ,设FQ与BC的夹角为θ3,FQ与OQ的夹角θ4,因为圆弧BQ与QD的长度相等,所以∠BOQ=45°,因为所有入射光平行,所以所有折射光线平行,则θ3=90°-θ2=75° ,θ4=180°-θ3-∠BOQ=60°,由于θ4>C,所以射到Q点的光一定发生全反射.故B正确.
C.由上可知对应的圆心角是60°,可得圆能从圆弧界面射出的圆弧长度为.故C正确.
D.当光线沿AP射出时,所用时间最长,根据几何关系可得:,速度为:,传播的时间为:
故D错误.
2.AD
【详解】
A、光子的频率由光源决定,与介质无关,所以光从真空射入光纤,光子的频率不变;故A正确.
B、光通过此光纤到达小截面的最短距离为L,光在光纤中的传播速度,则光通过此光纤到达小截面的最短时间为;故B错误.
C、通过光纤侧面全反射后再从上方截面射出的光束与垂直射出上方截面的光束不平行;故C错误.
D、设临界角为C,则到达光纤侧面光线入射角等于,当,即有,则光在第一次到达光纤侧面时发生全反射,不会从光纤侧面射出;故D正确.
故选AD.
【点睛】
解决本题的关键是掌握全反射现象的条件和临界角公式,结合几何知识进行分析.要注意光的频率与介质无关,而光速与介质有关.
3.ABC
【解析】
【详解】
所有色光都能反射,则由反射定律可知,不同色光的反射角均相同,因此甲光束仍为复色光,而乙光束、丙光束由于折射率不同导致偏折分离,因此为单色光,A正确;由图知,光束乙的偏折程度大于光束丙,根据折射定律可知光束乙的折射率大于光束丙的折射率,B正确;一束由两种色光混合的复色光沿AO方向射出,经过折射、反射、再折射后,光线仍是平行,因为第一次折射时的折射角与第二次折射时的入射角是相等的,反射时反射角与入射角相等,所以由光路可逆可得出射光线平行。如果减小角,光束甲、乙、丙仍保持平行,C正确;光束乙的折射率大于光束丙,则光束乙的频率大于光束丙,光束乙的波长小于光束丙的波长,而双缝干涉条纹间距与波长成正比,则双缝干涉实验中光束乙产生的条纹间距比光束丙小,D错误;根据,则光在玻璃中的传播时间,因两光束的折射角r不同,所以在该透明材料中传播的时间t不相等,E错误。
4.ABD
【详解】
A.光导纤维有内、外两层材料,其中内层是光密介质,外层是光疏介质,故A正确;
B.在太阳光照射下,水面上油膜前后表面反射光,频率相同,出现彩色是因为光的薄膜干涉现象,故B正确;
C.根据电磁波谱的特点可知,红外线的波长比紫外线的波长要长,故C错误;
D.根据
可知,紫光的频率大,临界角小,在不断增大入射角的过程中,水面上紫光比红光先消失,故D正确;
E.红光的波长长于紫光波长,根据
可知在同一装置上做双缝干涉实验,红光的相邻两个亮条纹的中心间距大于紫光的相邻两个亮条纹的中心间距,故E错误。
故选ABD。
5.A
【解析】
【详解】
凸透镜成像是折射成像,根据光路的可逆性可知,把一个点光源置于B点,发出两条光线沿着原光线返回,折射光线依然沿着原来的光路,故经凸透镜折射后反向延长线在A点,故成虚像于A点,故A正确,B,C,D错误;故选A.
【点睛】
本题关键明确凸透镜成像是折射成像,折射成像光路是可逆的.
6.B
【详解】
由视深与实深的关系式 可知b光的折射率最小,故③正确;c光从水下照亮水面的面积比a的大说明c光不容易发生全反射,即c光的折射率比a光的小,其频率也小于a的频率,故①错误,综上可知nb
【详解】
A.在玻璃幕墙表面镀一定厚度的金属氧化物,利用镜面反射使外面的人看不到幕墙里面的情况,A错误;
B.红外线的频率与固体物质分子的固有频率接近,容易引起分子共振,产生内能,B错误;
C.来回抖动带电的梳子,产生变化的电场,变化的电场产生变化的磁场,变化的电场和变化的磁场交替产生,形成电磁波,C正确;
D.地面上两北斗卫星导航终端同时发出定位申请信号,在高速运行的卫星上看两信号不是同时的,D错误。
故选C。
8.C
【详解】
设光的入射角为,折射角为,则根据折射定律有
又因为
设圆的直径为,则光在玻璃砖中的运动的距离为,光在玻璃砖中运动的时间为
将以上式子联立后求得
由于两种单色光的入射角相等,所以它们在玻璃砖中运动的时间相同。
故选C。
9.B
【详解】
光线由空气进入玻璃砖中时,入射角大于折射角,由玻璃砖射入空气时,入射角小于折射角,由临界角计算公式得
入射角50°大于临界角,将发生全反射。
ACD错误,B正确。
故选B。
10.D
【详解】
A.自行车“尾灯”为全反射棱镜,利用光的全反射现象,故A错误;
B.当波源与观察者相互远离时,根据多普勒效应,可知观察者接收到的频率减小,但是波源的频率不变,故B错误;
C.只有狭缝宽度与波长相差不多或比波长小的情况下,才发生明显衍射现象,故C错误;
D.用透明的标准样板和单色光检查工件平面的平整度,利用了光的薄膜干涉现象。故D正确。
故选D。
11.A
【详解】
光路图如图,设第一次折射角为r,全反射临界角为C,折射率为n。由折射定律有 ,得: ,又
对图中△ABO,由正弦定理得:,则得: 可解得i=30°,所以为保证在内壁处光不会进入中空部分,入射角i应满足i≥30°,故选A。
点睛:本题考查了光的折射、全反射的知识,解题时要正确画出光路图,找到恰好发生全反射的临界光线;能正确充分利用数学知识是解决此类问题的关键。
12.C
【详解】
A.反射光束1和折射光束2恰好垂直,由几何知识可求得此时的折射角为,由折射定律可得,玻璃的折射率为
可求得:,故A错误;
B.同一单色光,在不同介质中传播时,速度不同,但频率相同,故B错误,C正确;
D.光从光密介质进入光疏介质,当入射角等于或大于临界角时,将发生全反射现象,根据公式
由题可求得该单色光从玻璃进入空气时的临界角
到范围内有该值存在,所以当时,将发生全反射,故D错误。
故选C。
13.B
【详解】
A.如图所示
根据几何关系
,
折射率
绿光在采光球中的传播速度为
故A错误;
B.红光折射率小,折射角大,则红光一定能从N点上方射出,故B正确;
C.紫光不可能直接折射经过O点,如果过的话,折射角为0°,故C错误;
D.光由光密到光疏可能发生全反射,则涂层折射率应大于管壁折射率,故D错误。
故选B。
14.B
【详解】
玻璃折射率为,由临界角公式得
可得出玻璃砖的临界角,则当光线垂直直角边进入玻璃砖,射到斜边上时入射角为45°,光线能发生全反射,故可知B图可产生如图所示的效果,故选B。
15.C
【详解】
A.由图可知,玻璃砖对a光的折射率大于b光的折射率,所以a光的频率较大,A错误;
B.,由干涉条纹间距公式
可知b光的干涉条纹间距较大,B错误;
C.连接B、D;C、D,设,,设玻璃砖半径为R,则有
,
设玻璃砖对a光的折射率为,对b光的折射率为,则有
,
故a光和b光在玻璃砖的传播时间为
,
设复色光从真空射入玻璃砖时的入射角为,则有
,
联立以上各式解得
C正确;
D.a光和b光在水中传播时有
由
可知b光的全反射临界角较大,所以b光照亮的范围大,D错误。
故选C。
16.C
【详解】
A.红光在介质中传播的速度
选项A错误;
B.α不是入射角,由可知,红光的全反射角为60° ,紫光的全反射角为45°,所以当α逐渐变大的过程中,入射角逐渐变小,红光和紫光均不会发生全反射,B错误;
C.当α=53°时,对应的入射角:i=37°,光在屏幕AF上出现了两个亮斑分别是红色光与紫色光的紫色光,所以在AM区域的亮斑P1为红色,在AN区域的亮斑P2为红色与紫色的混合色.画出如图光路图.
设折射角分别为r1和r2,两个光斑分别为P1、P2,根据折射定律:
得:
,
由几何知识可得:
解得:
同理解得:
所以:
故C正确;
D.同一单色光在不同的介质中传播时频率不变,D错误.
17.B
【详解】
AB.由光路的可逆性,假设光分别由B进入A和C,根据折射率的物理意义可知,折射率是反映介质对光线偏折程度的物理量,进入C的偏折程度大于进入A的偏折程度,可知C的折射率比A的大,B中的入射角最大,折射率最小,可得
nC>nA>nB
A错误,B正确;
CD.由可以判断出,光在B中传播的速度最大,在C中传播的速度最小,CD错误。
故选B。
18.(1);(2)
【详解】
(1)由题意可知,光线与AB面垂线的夹角为θ时,射向BC面的光线恰好发生全反射,光路图如图所示
设透明物质Ⅱ的临界角为C,由几何关系可知
解得
(2)由光的折射定律可得
由几何关系可得
联立解得
19.600
【解析】试题分析:先画出光路图,屏幕上的光点恰好消失时,入射角等于临界角,由几何关系和全反射临界角公式求折射率n,再由折射定律求得入射角。
画出如图所示的光路图所示:
设入射为α,OA是入射到平面镜上的光线,AD是法线,设, ,由几何关系得:
由折射定律得:
因为:
代入解得:
可得:α=600
试题分析:本题主要考查了折射和反射两种光学现象,根据折射定律和反射定律进行分析.对于平面镜,要充分利用对称性分析光路。
20.(1)(2)
【解析】
由题意可知,CE是圆的一个弦.因此经AE面反射后反射光垂直平分CE,则反射光刚好照射到圆心O,光路图如图所示.
由几何关系可知,光钱在AE面的入射角为60 ,由于光线刚好在AE面上发生全反射,则全反射的临界角:C=60
则玻璃对光的折射率:
由几何关系可知,光在AB面上折射的折射角为r=30 ,设入射角为i,则
求得:
②由几何关系,圆弧的直径为d,则AB长为
则光在玻璃种传播的距离
光在玻璃种传播的时间
点睛:本题的关键是要掌握有关折射率的两个公式和.解题时,要作出光路图,利用几何知识帮助解答.
21.(1);(2)
【详解】
(1)光路图如图所示
根据几何关系得
解得,故,所以为等边三角形
又
解得
所以
由折射定律得
解得
(2)由几何关系可得,该光线在球冠中的传播路程
可知光在球冠中的传播时间
联立解得
22.① ②
【详解】
①设入射角、折射角分别为、,鱼饵灯离水面深度为,作出光路如图
则有
,
据光的折射定律,解得
②当鱼饵灯离水面深度为时,水面PQ间恰无光射出,此时鱼饵灯与浮标的连线和竖直方向的夹角恰好为临界角C,则
解得
答案第1页,共2页
答案第1页,共2页
