24.1.3_弧、弦、圆心角
文档属性
| 名称 | 24.1.3_弧、弦、圆心角 |

|
|
| 格式 | zip | ||
| 文件大小 | 453.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-19 00:00:00 | ||
图片预览





文档简介
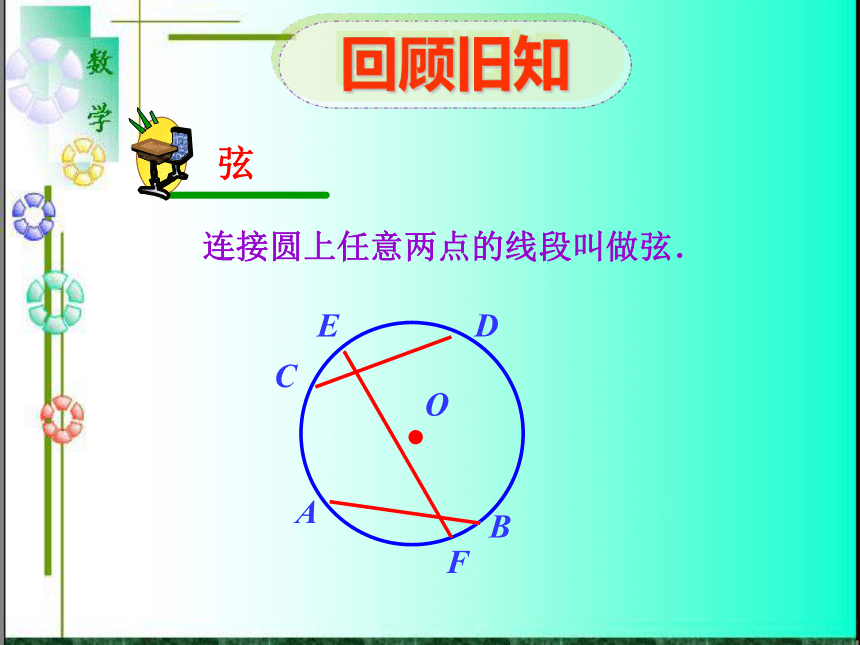
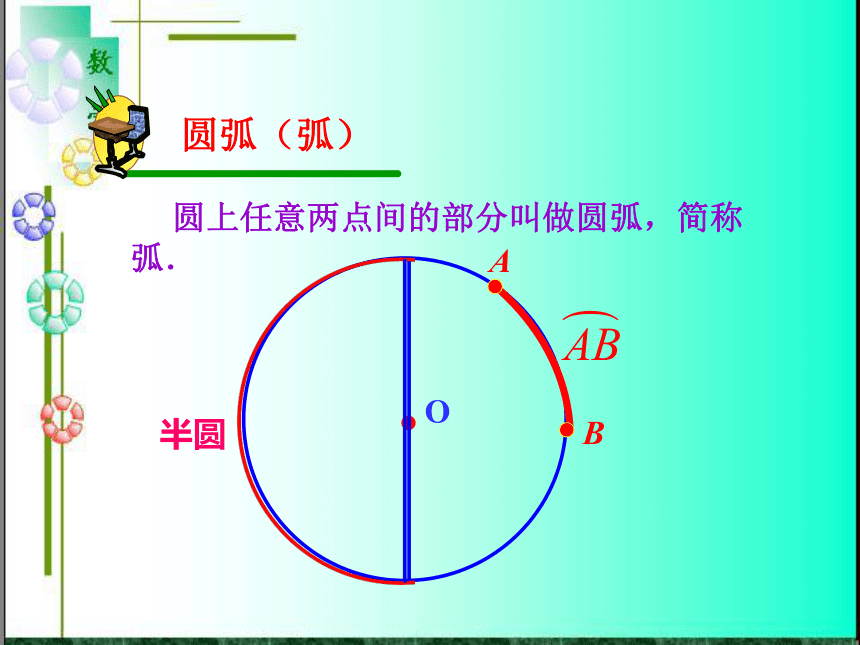
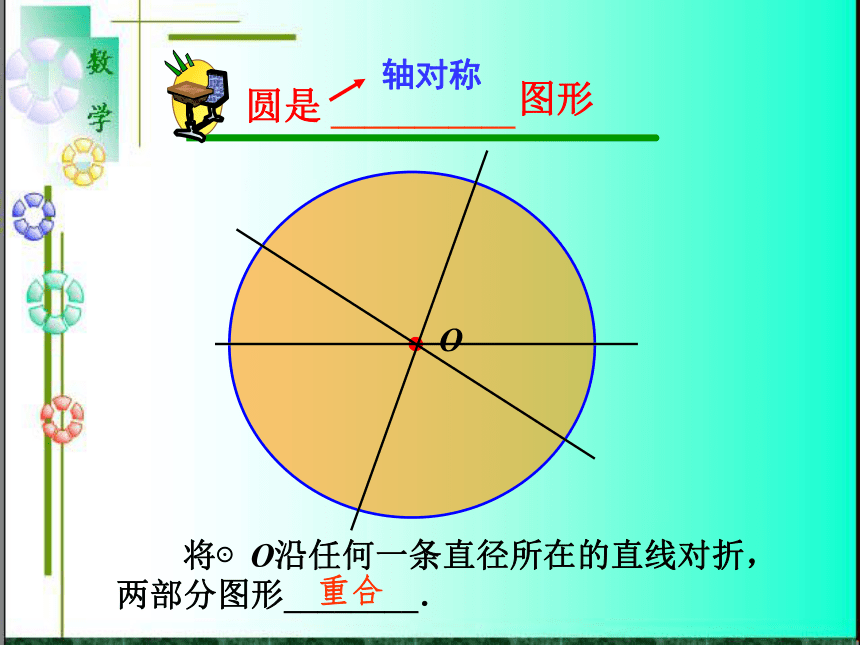
课件24张PPT。弦.弧.圆心角.回顾旧知弦连接圆上任意两点的线段叫做弦.O 圆上任意两点间的部分叫做圆弧,简称弧.圆弧(弧)OAB半圆圆是图形轴对称___________O 将⊙O沿任何一条直径所在的直线对折,两部分图形________.重合 将⊙O 绕圆心 O 顺时针旋转180°,这两个图形________.圆是图形轴对称中心对称___________O重合教学目标【知识与能力】 理解弦、弧等概念.
初步会运用这些概念判断真假命题. 逐步培养阅读教材、亲自动手实践,总结出新概念的能力.
进一步提高观察、比较、分析、概括知识的能力.【过程与方法】【情感态度与价值观】 培养通过动手实践发现问题的能力.
渗透“观察→分析→归纳→概括”的数学思想方法.教学重难点 对“等圆”、“等弧”的定义中的“互相重合”这一特征的理解.
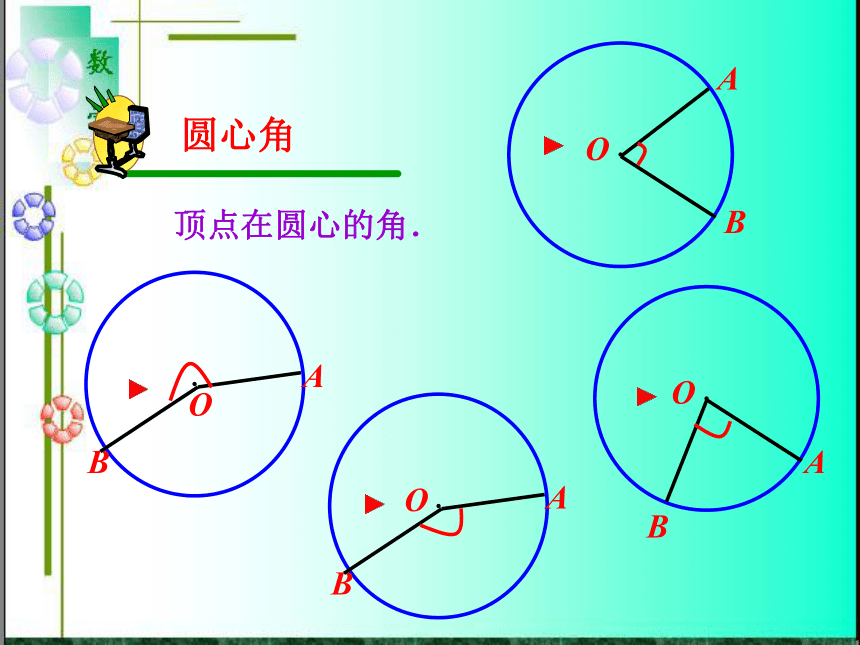
学生容易把长度相等的两条弧看成是等弧.顶点在圆心的角.圆心角圆心到弦的距离(即圆心到弦的垂线段的距离).弦心距 在⊙O中,分别作相等的圆心角∠AOB和∠A′OB′,将∠AOB旋转一定角度,使OA和O′A′重合. 你能发现哪些等量关系?·OAB·OABA′B′A′B′ 根据旋转的性质,∠AOB=∠A′OB′,射线 OA与OA′重合,OB与OB′重合.
而同圆的半径相等,OA=OA′,OB=OB′,
∴点 A与 A′重合,B与B′重合.·OABA′B′∴ 重合,AB与A′B′重合分析再根据△AOB≌△A′O′B′,OC=OC′ 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′弧、弦、圆心角的关系定理①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′两个圆心角相等两条弧相等两条弦相等两条弦心距相等 这四组关系分别轮换,其它关系是否成立?①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′弧、弦、圆心角关系定理的推论 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等.弧、弦、圆心角关系定理的推论①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′ 在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧相等,所对的弦的弦心距相等.①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′弧、弦、圆心角关系定理的推论 在同圆或等圆中,相等的弦心距所对的圆心角相等,所对的弧相等,所对的弦相等. 在同圆或等圆中,有一组关系相等,那么所对应的其它各组关系均分别相等.证明:∴AB=AC.又∠ACB=60°,∴AB=BC=CA.∴∠AOB=∠BOC=∠AOC.·ABCO 已知:在⊙O中, ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.解:已知:AB是⊙O 的直径, ∠COD=35°
求:∠AOE 的度数.课堂小结顶点在圆心的角.1. 圆心角 圆心到弦的距离(即圆心到弦的垂线段的距离).2. 弦心距 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.3. 弧、弦、圆心角的关系定理 1. AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.AB=CDAB=CD随堂练习 (4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
初步会运用这些概念判断真假命题. 逐步培养阅读教材、亲自动手实践,总结出新概念的能力.
进一步提高观察、比较、分析、概括知识的能力.【过程与方法】【情感态度与价值观】 培养通过动手实践发现问题的能力.
渗透“观察→分析→归纳→概括”的数学思想方法.教学重难点 对“等圆”、“等弧”的定义中的“互相重合”这一特征的理解.
学生容易把长度相等的两条弧看成是等弧.顶点在圆心的角.圆心角圆心到弦的距离(即圆心到弦的垂线段的距离).弦心距 在⊙O中,分别作相等的圆心角∠AOB和∠A′OB′,将∠AOB旋转一定角度,使OA和O′A′重合. 你能发现哪些等量关系?·OAB·OABA′B′A′B′ 根据旋转的性质,∠AOB=∠A′OB′,射线 OA与OA′重合,OB与OB′重合.
而同圆的半径相等,OA=OA′,OB=OB′,
∴点 A与 A′重合,B与B′重合.·OABA′B′∴ 重合,AB与A′B′重合分析再根据△AOB≌△A′O′B′,OC=OC′ 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′弧、弦、圆心角的关系定理①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′两个圆心角相等两条弧相等两条弦相等两条弦心距相等 这四组关系分别轮换,其它关系是否成立?①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′弧、弦、圆心角关系定理的推论 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等.弧、弦、圆心角关系定理的推论①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′ 在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧相等,所对的弦的弦心距相等.①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′弧、弦、圆心角关系定理的推论 在同圆或等圆中,相等的弦心距所对的圆心角相等,所对的弧相等,所对的弦相等. 在同圆或等圆中,有一组关系相等,那么所对应的其它各组关系均分别相等.证明:∴AB=AC.又∠ACB=60°,∴AB=BC=CA.∴∠AOB=∠BOC=∠AOC.·ABCO 已知:在⊙O中, ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.解:已知:AB是⊙O 的直径, ∠COD=35°
求:∠AOE 的度数.课堂小结顶点在圆心的角.1. 圆心角 圆心到弦的距离(即圆心到弦的垂线段的距离).2. 弦心距 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.3. 弧、弦、圆心角的关系定理 1. AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.AB=CDAB=CD随堂练习 (4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
同课章节目录
