北师大版九年级上 3.1 用树状图或表格求概率 同步练习(Word版含答案)
文档属性
| 名称 | 北师大版九年级上 3.1 用树状图或表格求概率 同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 386.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 14:35:11 | ||
图片预览



文档简介
北师大版同步练习 3.1 用树状图或表格求概率
一、选择题(共13小题;共65分)
1. 如图是两个完全相同的转盘,每个转盘被分成了面积相等的四个区域,每个区域内分别填上数字 ,,,.甲、乙两同学玩转盘游戏,规则如下:固定指针,同时转动两个转盘,任其自由转动,当转盘停止时,把左边转盘上指针指向的数字作为底数,把右边转盘上指针指向的数字作为指数,若指针指向分界线,则重新转动.若所得的幂为奇数,则甲获胜;若所得的幂为偶数,则乙获胜,那么该游戏
A. 对甲有利 B. 对乙有利
C. 公平 D. 公平性无法确定
2. 不透明的袋子中有两个小球,上面分别写着数字“”“”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为 的概率是
A. B. C. D.
3. 从 ,,, 这四个数中任取两个不同的数,则这两个数之和小于 的概率为
A. B. C. D.
4. 某中学有 名教师自愿献血,其中 人A型血, 人B型血, 人O型血,现从他们当中随机挑选 人参与献血,抽到的两人血型不同的概率为
A. B. C. D.
5. 红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是
A. 红红不是胜就是输,所以红红胜的概率为
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为
D. 娜娜胜的概率和两人出相同手势的概率一样
6. 不透明的袋子中有两个小球,上面分别写着数字“”“,除数字外两个小球无其他差别.从中随机摸出一个小球.记录其数字,放回并摇匀.再从中随机摸出一个小球,记录其数字.那么两次记录的数字之和为 的概率是
A. B. C. D.
7. 经过某个十字路口的汽车,可能直行,也可能左转或者右转,假设这 种可能性相同,现有两辆汽车经过这个十字路口,驶向相同方向的概率是
A. B. C. D.
8. 有四个一模一样的小球,其中三个小球上面分别标有数字 ,,,小明和小亮各摸一个,前一个人随机摸一个小球记下数字后放回,混合均匀,后一个人再随机摸一个小球,如果两人摸得小球的数字之和为 的概率为 ,那么第四个小球上的数字是
A. B. C. 或 D.
9. “田忌赛马”的故事家喻户晓,若田忌出马的顺序一直是下等马、中等马、上等马(上等马跑得最快,中等马次之,下等马跑得最慢),而齐王随机出马,则田忌获胜(三局两胜则为胜)的可能性是
A. B. C. D.
10. 某地新高考有一项“ 选 ”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为
A. B. C. D.
11. 九()班从小华、小琪、小明、小伟四人中随机抽出 人参加学校举行的乒乓球双打比赛,每人被抽到的可能性相等,则恰好抽到小华和小明的概率是
A. B. C. D.
12. 小刚一家三口参加“懂法纪,知敬畏”网上答题活动,每人获得一次抽奖机会:有三个彩球,分别代表特等奖,一等奖,谢谢参与,随机点击其中一个,翻开即为所得奖项.三人都随机点击其中一个,则三人获得的奖项都不相同的概率是
A. B. C. D.
13. 随机掷两枚质地均匀的硬币,落地后全部正面朝上的概率是
A. B. C. D.
二、填空题(共4小题;共20分)
14. 有两双完全相同的鞋,从中任取两只,恰好成为一双的概率为 .
15. 有三张大小、形状完全相同的卡片.卡片上分别写有数字 ,,,从这三张卡片中随机先后不放回地抽取两张,则两次抽出数字之和为奇数的概率是 .
16. 小明和小红玩抛硬币的游戏,连续抛两次.小明说:“若两次都是正面,则你赢;若两次是一正一反,则我赢”.则小红赢的概率是 ,小明赢的概率是 ,据此判断该游戏 .(填“公平”或“不公平”)
17. 《中国地名大会》是中央广播电视总台制作的中国首档大型地名文化类节目,旨在弘扬民族文化、提升民族自豪感.一个题目如下:
甲、乙两名同学都不会这个题目,就随机选择一个答案,他们选取的答案恰好都是正确答案 的概率为 .
三、解答题(共3小题;共39分)
18. 经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
19. 在一个口袋中装有 个完全相同的小球,把它们分别标号为 ,,,随机摸出一个小球后放回,再随机摸出一个小球,将两次摸出小球的标号相加.
(1)将所有的结果填入下表:
(2)求两次摸出小球的标号和等于 的概率
20. 在阳光体育活动时间,小莹、小芳和小刚到学校乒乓球室打乒乓球,当时只有一副空球拍,他们只能选两人打第一场.
(1)如果确定小芳打第一场,再随机选取一人打第一场,则恰好选中小刚的概率是 ;
(2)用“手心”、“手背”的方法决定哪两人打第一场.游戏规则是:三人同时伸“手心”、“手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始.这三人伸出“手心”或“手背”都是随机的,请用画树状图或列表的方法求小莹和小芳打第一场的概率.
答案
第一部分
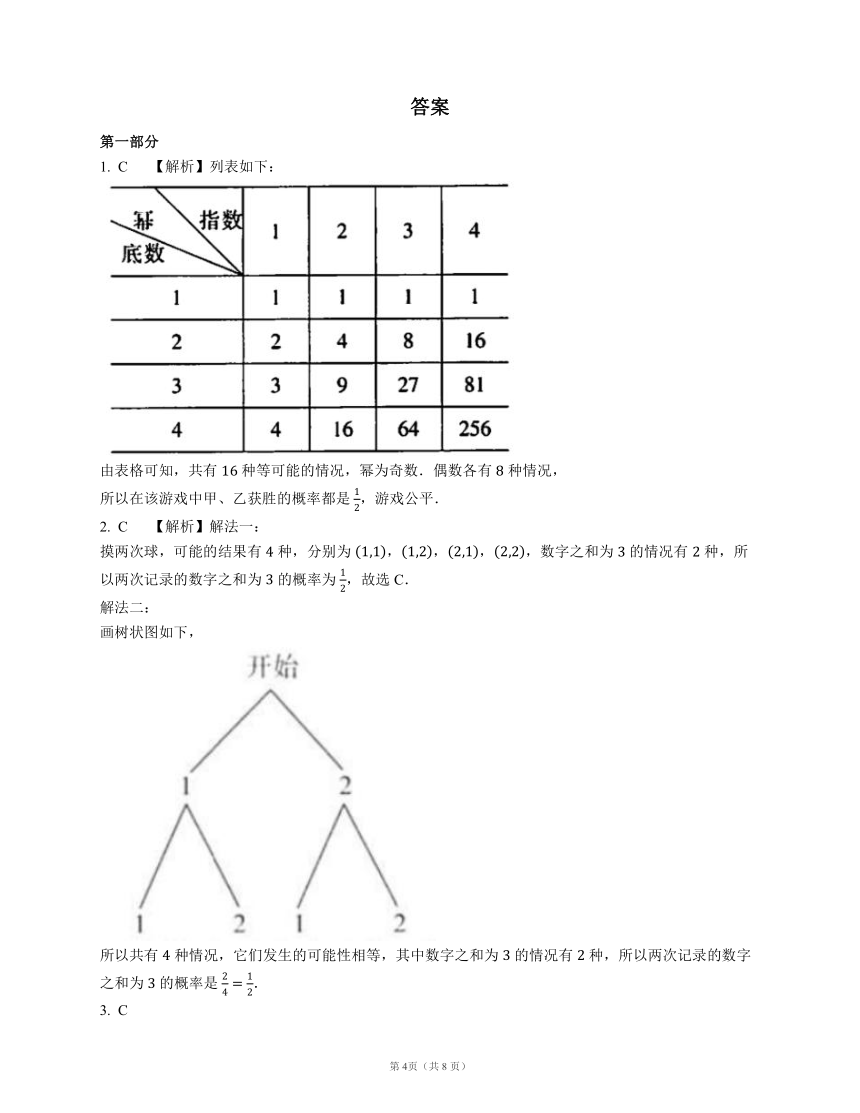
1. C 【解析】列表如下:
由表格可知,共有 种等可能的情况,幂为奇数.偶数各有 种情况,
所以在该游戏中甲、乙获胜的概率都是 ,游戏公平.
2. C 【解析】解法一:
摸两次球,可能的结果有 种,分别为 ,,,,数字之和为 的情况有 种,所以两次记录的数字之和为 的概率为 ,故选C.
解法二:
画树状图如下,
所以共有 种情况,它们发生的可能性相等,其中数字之和为 的情况有 种,所以两次记录的数字之和为 的概率是 .
3. C
4. C
5. A
【解析】红红和娜娜玩“锤子、剪刀、布”游戏,所有可能出现的结果列表如下:
由表格可知,共有 种等可能的情况.其中平局的有 种:(锤子,锤子),(剪刀,剪刀),(布,布);红红胜的有 种:(锤子,布),(剪刀,锤子),(布,剪刀);娜娜胜的有 种:(锤子,剪刀),(剪刀,布),(布,锤子).因此,红红和娜娜两人出相同手势的概率为 ,两人获胜的概率都为 .
6. C 【解析】列表如下:
由上表可知,共有 种等可能的结果,其中两次记录的数字之和为 的结果有 种,所以两次记录的数字之和为 的概率为 .
故选C.
7. A
8. C 【解析】设第四个小球上的数字为 ,画树状图如下:
共有 种等可能的结果,而两人摸得小球的数字之和为 的概率为 ,则两人摸得小球的数字之和为 的结果有 种.分析树状图知 ,当 时不符合,当 时,,,符合;当 时,,,符合,所以第四个小球上的数字为 或 .故选C.
9. D 【解析】当齐王的马随机出阵时,双方马的对阵情况如下:
分析可以知道,田忌赢得比赛的可能性是 .
10. A
【解析】设“物理、化学、政治、历史”分别用A,B,C,D表示,画树状图如下:
共有 种等可能的结果,其中李鑫和张锋恰好一人选物理,另一人选化学的结果有 种,
所以李鑫和张锋恰好一人选物理,另一人选化学的概率为 .
11. C 【解析】把小华、小琪、小明、小伟分别记为 ,,,,列表如下:
共有 个等可能的结果,恰好抽到小华和小明的结果有 个,
恰好抽到小华和小明的概率为 .
12. D 【解析】用 ,, 分别表示特等奖,一等奖和谢谢参与,画树状图如下:
由树状图可知,共有 种等可能的结果,三人获得的奖项都不相同的结果有 种
.故选D.
13. D 【解析】列表如下:
所有等可能的情况有 种,其中全部正面朝上的情况有 种,
则掷两枚质地均匀的硬币,落地后全部正面朝上的概率为 .
第二部分
14.
15.
【解析】列表得:
共有 种情况,取出的两张卡片上的数字之和为奇数的情况数为 种,
两次抽出数字之和为奇数的概率为 .
故答案为:.
16. ,,不公平
17.
【解析】列表如下:
由表格可知,共有 种等可能的结果,其中两人都选择 的结果有 种,
所以他们选取的答案恰好都是正确答案 的概率为 .
第三部分
18. (1) .
(2) .
(3) .
19. (1)
(2) 由表格可知,共有 种等可能的结果,其中两次摸出小球的标号和等于 的结果有 种,
两次摸出小球的标号和等于 的概率为 .
20. (1)
(2) 画树状图如图所示.
由树状图可知,共有 种等可能的结果,其中小莹和小芳伸出的手势恰好相同且与小刚不同的结果有 种,
小莹和小芳打第一场的概率为 .
第1页(共1 页)
一、选择题(共13小题;共65分)
1. 如图是两个完全相同的转盘,每个转盘被分成了面积相等的四个区域,每个区域内分别填上数字 ,,,.甲、乙两同学玩转盘游戏,规则如下:固定指针,同时转动两个转盘,任其自由转动,当转盘停止时,把左边转盘上指针指向的数字作为底数,把右边转盘上指针指向的数字作为指数,若指针指向分界线,则重新转动.若所得的幂为奇数,则甲获胜;若所得的幂为偶数,则乙获胜,那么该游戏
A. 对甲有利 B. 对乙有利
C. 公平 D. 公平性无法确定
2. 不透明的袋子中有两个小球,上面分别写着数字“”“”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为 的概率是
A. B. C. D.
3. 从 ,,, 这四个数中任取两个不同的数,则这两个数之和小于 的概率为
A. B. C. D.
4. 某中学有 名教师自愿献血,其中 人A型血, 人B型血, 人O型血,现从他们当中随机挑选 人参与献血,抽到的两人血型不同的概率为
A. B. C. D.
5. 红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是
A. 红红不是胜就是输,所以红红胜的概率为
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为
D. 娜娜胜的概率和两人出相同手势的概率一样
6. 不透明的袋子中有两个小球,上面分别写着数字“”“,除数字外两个小球无其他差别.从中随机摸出一个小球.记录其数字,放回并摇匀.再从中随机摸出一个小球,记录其数字.那么两次记录的数字之和为 的概率是
A. B. C. D.
7. 经过某个十字路口的汽车,可能直行,也可能左转或者右转,假设这 种可能性相同,现有两辆汽车经过这个十字路口,驶向相同方向的概率是
A. B. C. D.
8. 有四个一模一样的小球,其中三个小球上面分别标有数字 ,,,小明和小亮各摸一个,前一个人随机摸一个小球记下数字后放回,混合均匀,后一个人再随机摸一个小球,如果两人摸得小球的数字之和为 的概率为 ,那么第四个小球上的数字是
A. B. C. 或 D.
9. “田忌赛马”的故事家喻户晓,若田忌出马的顺序一直是下等马、中等马、上等马(上等马跑得最快,中等马次之,下等马跑得最慢),而齐王随机出马,则田忌获胜(三局两胜则为胜)的可能性是
A. B. C. D.
10. 某地新高考有一项“ 选 ”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为
A. B. C. D.
11. 九()班从小华、小琪、小明、小伟四人中随机抽出 人参加学校举行的乒乓球双打比赛,每人被抽到的可能性相等,则恰好抽到小华和小明的概率是
A. B. C. D.
12. 小刚一家三口参加“懂法纪,知敬畏”网上答题活动,每人获得一次抽奖机会:有三个彩球,分别代表特等奖,一等奖,谢谢参与,随机点击其中一个,翻开即为所得奖项.三人都随机点击其中一个,则三人获得的奖项都不相同的概率是
A. B. C. D.
13. 随机掷两枚质地均匀的硬币,落地后全部正面朝上的概率是
A. B. C. D.
二、填空题(共4小题;共20分)
14. 有两双完全相同的鞋,从中任取两只,恰好成为一双的概率为 .
15. 有三张大小、形状完全相同的卡片.卡片上分别写有数字 ,,,从这三张卡片中随机先后不放回地抽取两张,则两次抽出数字之和为奇数的概率是 .
16. 小明和小红玩抛硬币的游戏,连续抛两次.小明说:“若两次都是正面,则你赢;若两次是一正一反,则我赢”.则小红赢的概率是 ,小明赢的概率是 ,据此判断该游戏 .(填“公平”或“不公平”)
17. 《中国地名大会》是中央广播电视总台制作的中国首档大型地名文化类节目,旨在弘扬民族文化、提升民族自豪感.一个题目如下:
甲、乙两名同学都不会这个题目,就随机选择一个答案,他们选取的答案恰好都是正确答案 的概率为 .
三、解答题(共3小题;共39分)
18. 经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
19. 在一个口袋中装有 个完全相同的小球,把它们分别标号为 ,,,随机摸出一个小球后放回,再随机摸出一个小球,将两次摸出小球的标号相加.
(1)将所有的结果填入下表:
(2)求两次摸出小球的标号和等于 的概率
20. 在阳光体育活动时间,小莹、小芳和小刚到学校乒乓球室打乒乓球,当时只有一副空球拍,他们只能选两人打第一场.
(1)如果确定小芳打第一场,再随机选取一人打第一场,则恰好选中小刚的概率是 ;
(2)用“手心”、“手背”的方法决定哪两人打第一场.游戏规则是:三人同时伸“手心”、“手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始.这三人伸出“手心”或“手背”都是随机的,请用画树状图或列表的方法求小莹和小芳打第一场的概率.
答案
第一部分
1. C 【解析】列表如下:
由表格可知,共有 种等可能的情况,幂为奇数.偶数各有 种情况,
所以在该游戏中甲、乙获胜的概率都是 ,游戏公平.
2. C 【解析】解法一:
摸两次球,可能的结果有 种,分别为 ,,,,数字之和为 的情况有 种,所以两次记录的数字之和为 的概率为 ,故选C.
解法二:
画树状图如下,
所以共有 种情况,它们发生的可能性相等,其中数字之和为 的情况有 种,所以两次记录的数字之和为 的概率是 .
3. C
4. C
5. A
【解析】红红和娜娜玩“锤子、剪刀、布”游戏,所有可能出现的结果列表如下:
由表格可知,共有 种等可能的情况.其中平局的有 种:(锤子,锤子),(剪刀,剪刀),(布,布);红红胜的有 种:(锤子,布),(剪刀,锤子),(布,剪刀);娜娜胜的有 种:(锤子,剪刀),(剪刀,布),(布,锤子).因此,红红和娜娜两人出相同手势的概率为 ,两人获胜的概率都为 .
6. C 【解析】列表如下:
由上表可知,共有 种等可能的结果,其中两次记录的数字之和为 的结果有 种,所以两次记录的数字之和为 的概率为 .
故选C.
7. A
8. C 【解析】设第四个小球上的数字为 ,画树状图如下:
共有 种等可能的结果,而两人摸得小球的数字之和为 的概率为 ,则两人摸得小球的数字之和为 的结果有 种.分析树状图知 ,当 时不符合,当 时,,,符合;当 时,,,符合,所以第四个小球上的数字为 或 .故选C.
9. D 【解析】当齐王的马随机出阵时,双方马的对阵情况如下:
分析可以知道,田忌赢得比赛的可能性是 .
10. A
【解析】设“物理、化学、政治、历史”分别用A,B,C,D表示,画树状图如下:
共有 种等可能的结果,其中李鑫和张锋恰好一人选物理,另一人选化学的结果有 种,
所以李鑫和张锋恰好一人选物理,另一人选化学的概率为 .
11. C 【解析】把小华、小琪、小明、小伟分别记为 ,,,,列表如下:
共有 个等可能的结果,恰好抽到小华和小明的结果有 个,
恰好抽到小华和小明的概率为 .
12. D 【解析】用 ,, 分别表示特等奖,一等奖和谢谢参与,画树状图如下:
由树状图可知,共有 种等可能的结果,三人获得的奖项都不相同的结果有 种
.故选D.
13. D 【解析】列表如下:
所有等可能的情况有 种,其中全部正面朝上的情况有 种,
则掷两枚质地均匀的硬币,落地后全部正面朝上的概率为 .
第二部分
14.
15.
【解析】列表得:
共有 种情况,取出的两张卡片上的数字之和为奇数的情况数为 种,
两次抽出数字之和为奇数的概率为 .
故答案为:.
16. ,,不公平
17.
【解析】列表如下:
由表格可知,共有 种等可能的结果,其中两人都选择 的结果有 种,
所以他们选取的答案恰好都是正确答案 的概率为 .
第三部分
18. (1) .
(2) .
(3) .
19. (1)
(2) 由表格可知,共有 种等可能的结果,其中两次摸出小球的标号和等于 的结果有 种,
两次摸出小球的标号和等于 的概率为 .
20. (1)
(2) 画树状图如图所示.
由树状图可知,共有 种等可能的结果,其中小莹和小芳伸出的手势恰好相同且与小刚不同的结果有 种,
小莹和小芳打第一场的概率为 .
第1页(共1 页)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
