2021-2022学年人教版七年级数学下册 寒假预习检测卷 5.1相交线(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册 寒假预习检测卷 5.1相交线(word版含答案) | 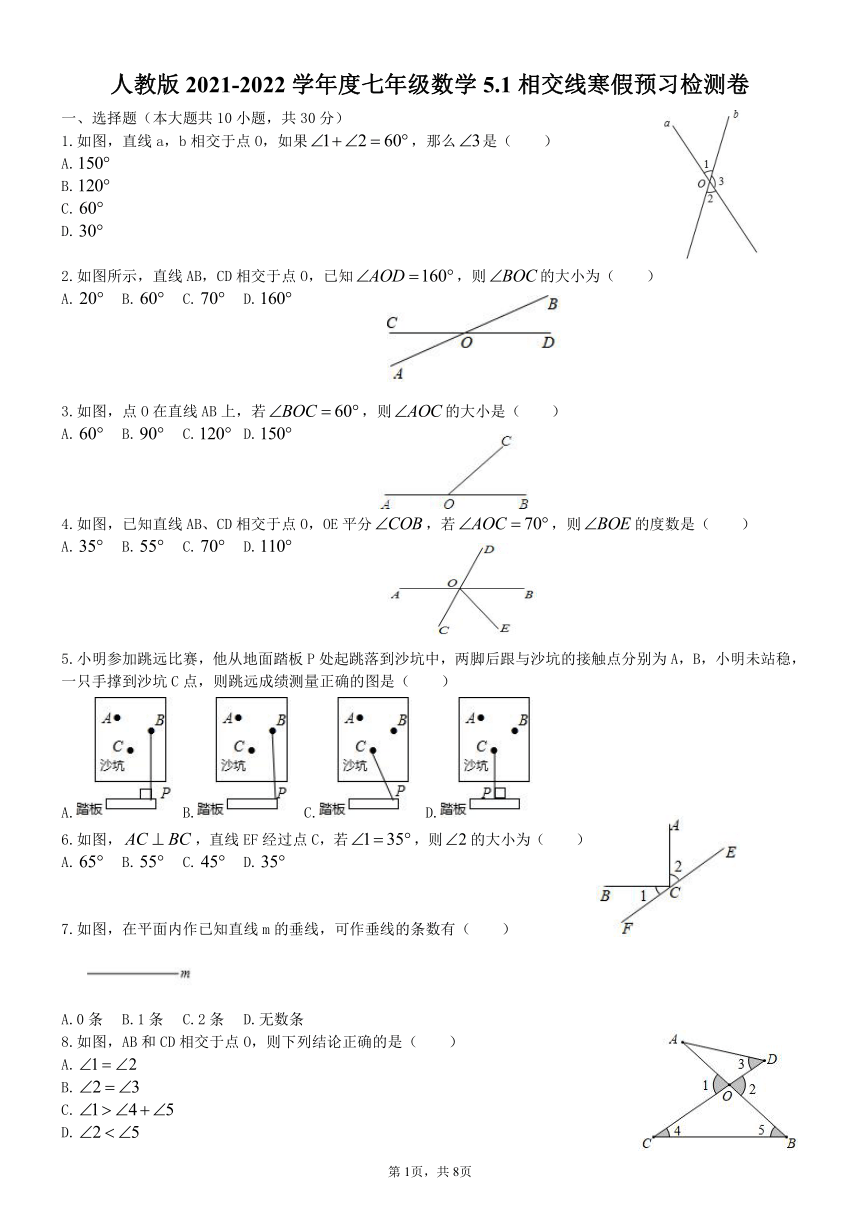 | |
| 格式 | docx | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 14:54:23 | ||
图片预览


文档简介
人教版2021-2022学年度七年级数学5.1相交线寒假预习检测卷
一、选择题(本大题共10小题,共30分)
1.如图,直线a,b相交于点O,如果,那么是( )
A.
B.
C.
D.
2.如图所示,直线AB,CD相交于点O,已知,则的大小为( )
A. B. C. D.
3.如图,点O在直线AB上,若,则的大小是( )
A. B. C. D.
4.如图,已知直线AB、CD相交于点O,OE平分,若,则的度数是( )
A. B. C. D.
5.小明参加跳远比赛,他从地面踏板P处起跳落到沙坑中,两脚后跟与沙坑的接触点分别为A,B,小明未站稳,一只手撑到沙坑C点,则跳远成绩测量正确的图是( )
A. B. C. D.
6.如图,,直线EF经过点C,若,则的大小为( )
A. B. C. D.
7.如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
8.如图,AB和CD相交于点O,则下列结论正确的是( )
A.
B.
C.
D.
9.如图,直线AD,BE被直线BF和AC所截,则的同位角和的内错角分别是( )
A., B., C., D.,
10.如图,与是同旁内角的是( )
A. B.
C. D.
二、填空题(本大题共5小题,共15分)
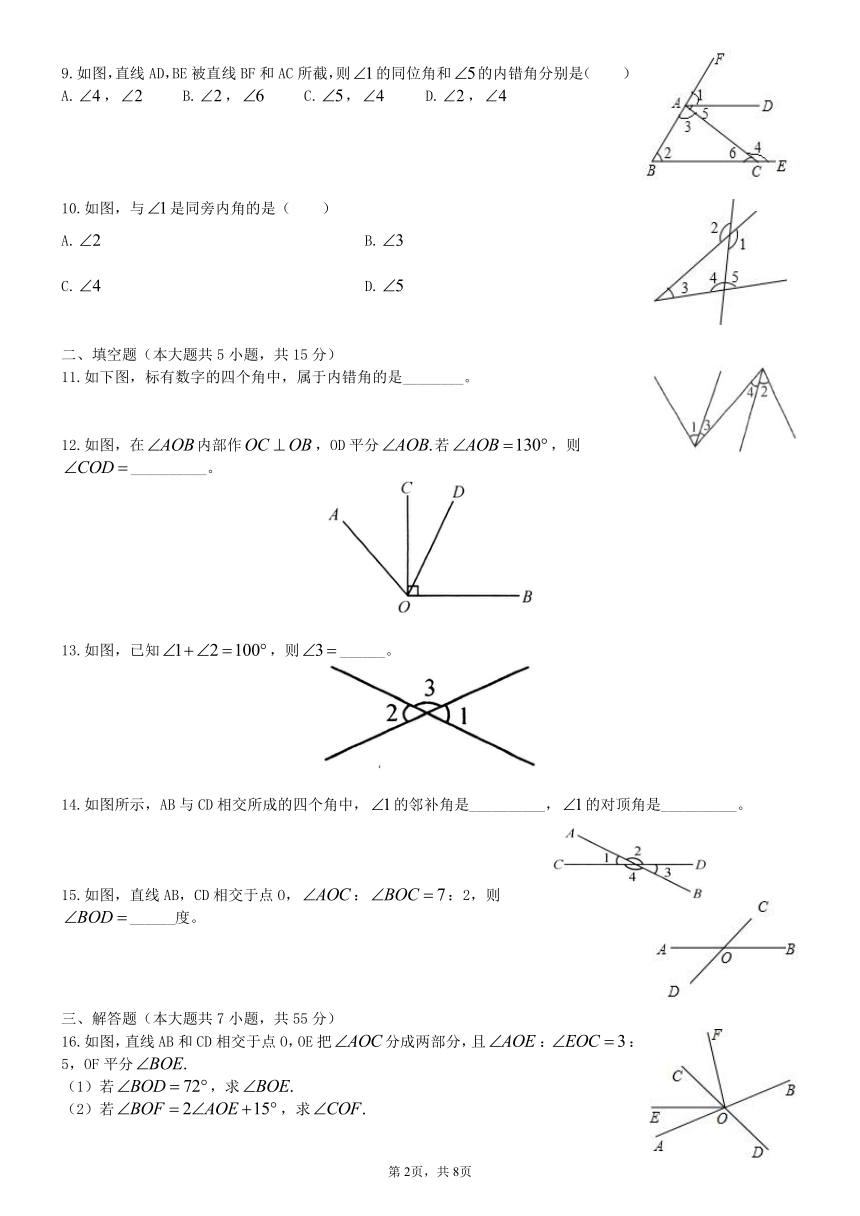
11.如下图,标有数字的四个角中,属于内错角的是________。
12.如图,在内部作,OD平分若,则__________。
13.如图,已知,则______。
14.如图所示,AB与CD相交所成的四个角中,的邻补角是__________,的对顶角是__________。
15.如图,直线AB,CD相交于点O,::2,则______度。
三、解答题(本大题共7小题,共55分)
16.如图,直线AB和CD相交于点O,OE把分成两部分,且::5,OF平分
(1)若,求
(2)若,求
17.如图,两条直线a,b相交.
(1)如果,求,的度数;
(2)如果,求,的度数.
18.平面内两条直线EF、CD相交于点O,,OC恰好平分
(1)如图1,若,求的度数;
(2)在图1中,若,请求出的度数用含有x的式子表示,并写出和的数量关系;
(3)如图2,当OA,OB在直线EF的同侧时,和的数量关系是否会发生改变?若不变,直接写出它们之间的数量关系;若发生变化,请说明理由.
19.如图,已知直线AB,CD,EF相交于点O,,,求和的度数.
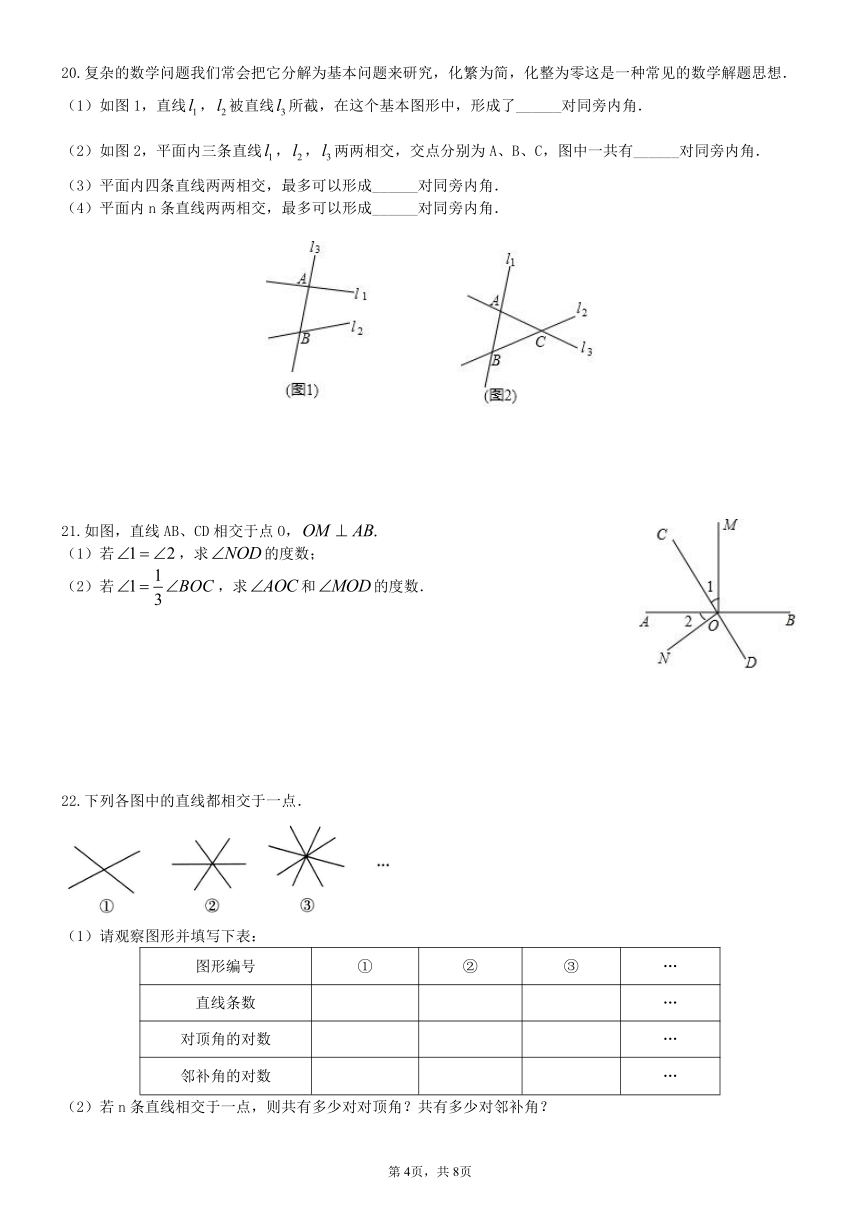
20.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为A、B、C,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内n条直线两两相交,最多可以形成______对同旁内角.
21.如图,直线AB、CD相交于点O,
(1)若,求的度数;
(2)若,求和的度数.
22.下列各图中的直线都相交于一点.
(1)请观察图形并填写下表:
图形编号 ① ② ③ …
直线条数 …
对顶角的对数 …
邻补角的对数 …
(2)若n条直线相交于一点,则共有多少对对顶角?共有多少对邻补角?
参考答案
1.A
2.D
3.C
4.B
5.D
6.B
7.D
8.A
9.B
10.D
11.和
12.
13.
14.和;
15.140
16.解:由对顶角相等,得,
由OE把分成两部分且::5,得,
由邻补角,得;
由OF平分,得
由邻补角,得,即,
解得
,,
17.解:,,
,
又与是对顶角,
;
,,
,
,
,
,
又,
18.解:,
,
平分,
,
,
,
;
,
,
平分,
,
,
,
;
;
不变,
19.解:和互为对顶角,,
,
,
,
20.解:直线,被直线所截,在这个基本图形中,形成了2对同旁内角.
平面内三条直线,,两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
平面内四条直线两两相交,最多可以形成24对同旁内角.
平面内n条直线两两相交,最多可以形成对同旁内角
所以答案为:;;;
21.解:,
,
,
,
;
,
,
,
,
解得,
,
22.解:填表如下:
图形编号 ① ② ③ …
直线条数 2 3 4 …
对顶角的对数 2 6 12 …
邻补角的对数 4 12 24 …
由中表格可发现:对顶角的对数是直线条数的倍,邻补角的对数是对顶角对数的2倍,
条直线相交于一点,对顶角共有对,邻补角共有对。第2页,共3页
第1页,共3页
一、选择题(本大题共10小题,共30分)
1.如图,直线a,b相交于点O,如果,那么是( )
A.
B.
C.
D.
2.如图所示,直线AB,CD相交于点O,已知,则的大小为( )
A. B. C. D.
3.如图,点O在直线AB上,若,则的大小是( )
A. B. C. D.
4.如图,已知直线AB、CD相交于点O,OE平分,若,则的度数是( )
A. B. C. D.
5.小明参加跳远比赛,他从地面踏板P处起跳落到沙坑中,两脚后跟与沙坑的接触点分别为A,B,小明未站稳,一只手撑到沙坑C点,则跳远成绩测量正确的图是( )
A. B. C. D.
6.如图,,直线EF经过点C,若,则的大小为( )
A. B. C. D.
7.如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
8.如图,AB和CD相交于点O,则下列结论正确的是( )
A.
B.
C.
D.
9.如图,直线AD,BE被直线BF和AC所截,则的同位角和的内错角分别是( )
A., B., C., D.,
10.如图,与是同旁内角的是( )
A. B.
C. D.
二、填空题(本大题共5小题,共15分)
11.如下图,标有数字的四个角中,属于内错角的是________。
12.如图,在内部作,OD平分若,则__________。
13.如图,已知,则______。
14.如图所示,AB与CD相交所成的四个角中,的邻补角是__________,的对顶角是__________。
15.如图,直线AB,CD相交于点O,::2,则______度。
三、解答题(本大题共7小题,共55分)
16.如图,直线AB和CD相交于点O,OE把分成两部分,且::5,OF平分
(1)若,求
(2)若,求
17.如图,两条直线a,b相交.
(1)如果,求,的度数;
(2)如果,求,的度数.
18.平面内两条直线EF、CD相交于点O,,OC恰好平分
(1)如图1,若,求的度数;
(2)在图1中,若,请求出的度数用含有x的式子表示,并写出和的数量关系;
(3)如图2,当OA,OB在直线EF的同侧时,和的数量关系是否会发生改变?若不变,直接写出它们之间的数量关系;若发生变化,请说明理由.
19.如图,已知直线AB,CD,EF相交于点O,,,求和的度数.
20.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为A、B、C,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内n条直线两两相交,最多可以形成______对同旁内角.
21.如图,直线AB、CD相交于点O,
(1)若,求的度数;
(2)若,求和的度数.
22.下列各图中的直线都相交于一点.
(1)请观察图形并填写下表:
图形编号 ① ② ③ …
直线条数 …
对顶角的对数 …
邻补角的对数 …
(2)若n条直线相交于一点,则共有多少对对顶角?共有多少对邻补角?
参考答案
1.A
2.D
3.C
4.B
5.D
6.B
7.D
8.A
9.B
10.D
11.和
12.
13.
14.和;
15.140
16.解:由对顶角相等,得,
由OE把分成两部分且::5,得,
由邻补角,得;
由OF平分,得
由邻补角,得,即,
解得
,,
17.解:,,
,
又与是对顶角,
;
,,
,
,
,
,
又,
18.解:,
,
平分,
,
,
,
;
,
,
平分,
,
,
,
;
;
不变,
19.解:和互为对顶角,,
,
,
,
20.解:直线,被直线所截,在这个基本图形中,形成了2对同旁内角.
平面内三条直线,,两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
平面内四条直线两两相交,最多可以形成24对同旁内角.
平面内n条直线两两相交,最多可以形成对同旁内角
所以答案为:;;;
21.解:,
,
,
,
;
,
,
,
,
解得,
,
22.解:填表如下:
图形编号 ① ② ③ …
直线条数 2 3 4 …
对顶角的对数 2 6 12 …
邻补角的对数 4 12 24 …
由中表格可发现:对顶角的对数是直线条数的倍,邻补角的对数是对顶角对数的2倍,
条直线相交于一点,对顶角共有对,邻补角共有对。第2页,共3页
第1页,共3页
