7.5.1三角形的内角和定理(1) 课件(共30张PPT)
文档属性
| 名称 | 7.5.1三角形的内角和定理(1) 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1001.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 12:29:07 | ||
图片预览








文档简介
(共30张PPT)
7.5.1三角形的内角和定理(1)
第七章
平行线的证明
2021-2022学年八年级数学上册同步课件
学习目标
1.证明三角形内角和定理,并能运用这些定理解决简单的问题.
2.经历探索与证明的过程,进一步发展推理能力.
3.在一题多解、一题多变中,积累解决几何问题的经验,提升解决问题的能力.
导入新课
三角形家族的问题
不对!是我们钝角三角形的内角和最大!
我们锐角三角形的内角和度数最大!
你们别吵了!还是我们直角三角形的内角和最大!
讲授新课
三角形的内角和定理的证明
一
问题1:你觉得他们谁说的对
问题2:你还记得吗?小学我们是怎样探索三角形内角和的?
你能给大家说说或者展示一下吗?
讲授新课
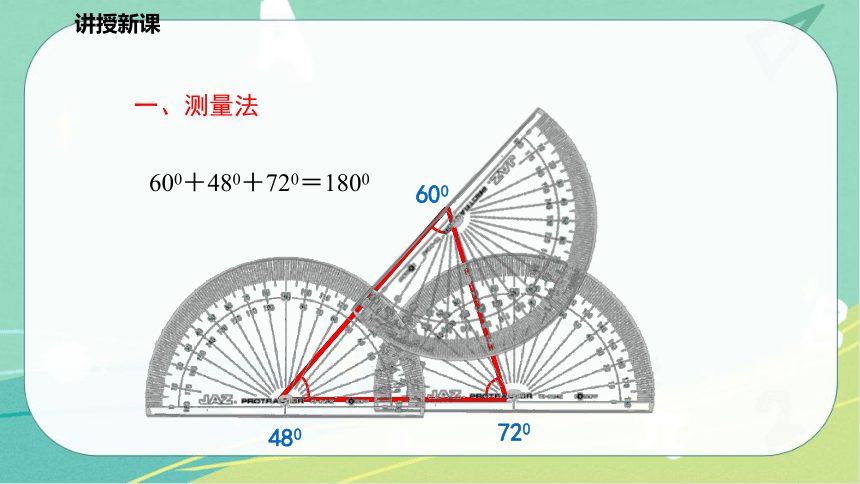
一、测量法
480
720
600
600+480+720=1800
讲授新课
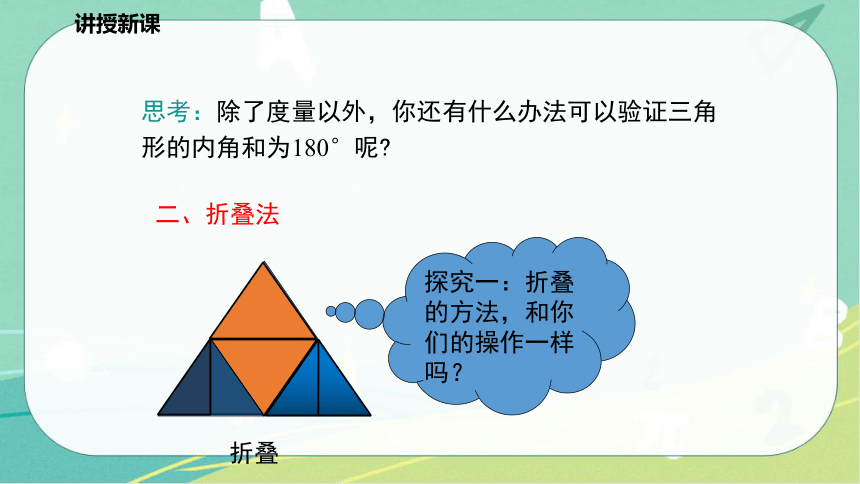
思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢
折叠
探究一:折叠的方法,和你们的操作一样吗?
二、折叠法
讲授新课
三、剪拼法(撕拼法)
A
B
C
2
1
讲授新课
A
C
B
A
C
B
E
旋转平移
问题1:如图,当∠A移到∠1的位置时,残边CD和边AB有何位置关系?为什么?
问题2:在剪拼法中,通过移动角拼成了一个平角;如果不实际移动角,那么你还有其它方法可以达到同样的效果吗
讲授新课
A
C
B
E
D
A
C
B
1
2
3
E
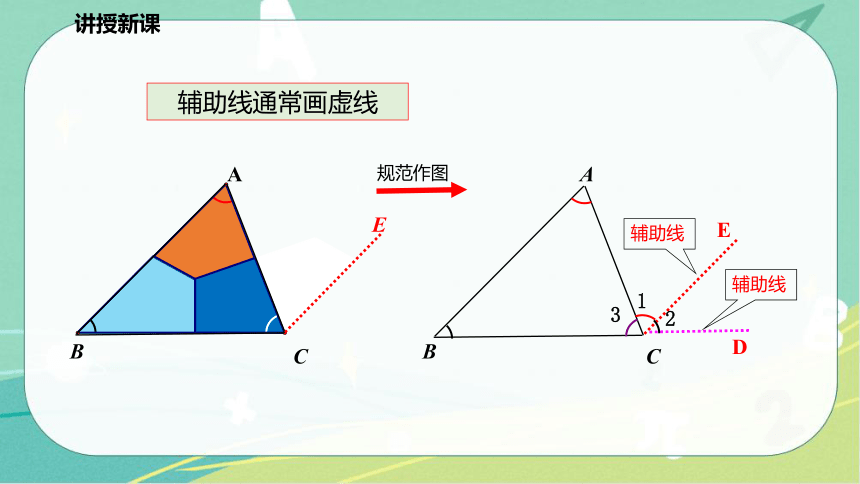
规范作图
辅助线
辅助线通常画虚线
辅助线
讲授新课
思路总结
添加辅助线
三角形内角和
转化
平角/同旁内角
讲授新课
知识要点
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
讲授新课
你还有什么方法可以达到同样的效果?
可以用“两直线平行,同旁内角互补”来说明.可以通过作辅助线实现移动的效果,例如延长BC到点D,过点C作射线CE∥BA,这样就相当于把∠A移到了∠1的位置,∠B移到了∠2的位置.这里的CD、CE称为辅助线,辅助线通常画成虚线。
讲授新课
想一想:还有其他方法证明三角形内角和定理吗?
讲授新课
已知:如图,在△ABC中.
求证:∠A+∠B+∠C=180°.
证明:(如图①)过点A作PQ∥BC,
则∠1=∠B,∠2=∠C
(两直线平行,内错角相等).
∵∠1+∠BAC+∠2=180°(平角的定义)
∴∠B+∠BAC+∠C=180°(等量代换).
讲授新课
已知:如图,在△ABC中.
求证:∠A+∠B+∠C=180°.
证明:(如图②)过点C作CE∥AB,
则∠1=∠A(两直线平行,内错角相等),∠B+∠BCE=180°
(两直线平行,同旁内角互补).
∵∠BCE=∠BCA+∠1,
∴∠B+∠BCA+∠1=180°(等量代换),
∴∠B+∠BAC+∠A=180°(等量代换).
讲授新课
已知:如图,在△ABC中.
求证:∠A+∠B+∠C=180°.
证明:(如图③)过BC边上的一点P作QP∥AC,RP∥AB,交AB于Q,交AC于R,
则∠1=∠B,∠2=∠C
(两直线平行,同位角相等).
∠A=∠BQP=∠QPR
(两直线平行,同位角相等,内错角相等).
∵∠1+∠2+∠QPR=180°(平角的定义),
∴∠A+∠B+∠C=180°(等量代换).
讲授新课
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
三角形的内角和定理的运用
二
讲授新课
【变式题】如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°-∠A-∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
讲授新课
例2 如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°-∠FEA-∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°-∠CFD-∠FCD=40°.
讲授新课
基本图形
由三角形的内角和定理易得∠A+∠B=∠C+∠D.
由三角形的内角和定理易得∠1+∠2=∠3+∠4.
总结归纳
讲授新课
例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°,
∠C为(x + 15)°, 从而有
3x + x +(x + 15)= 180.
解得 x = 33.
所以 3x = 99 , x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°.
几何问题借助方程来解. 这是一个重要的数学思想.
讲授新课
【变式题】在△ABC中,∠A= ∠B= ∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数.
解析:根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,∠ACD,最后根据角平分线的定义求出∠ACE即可求得∠DCE的度数.
比例关系可考虑用方程思想求角度.
讲授新课
解:∵∠A= ∠B= ∠ACB,
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°-90°-30°=60°.
∵CE是∠ACB的平分线,
∴∠ACE= ×90°=45°,
∴∠DCE=∠ACD-∠ACE=60°-45°=15°.
当堂检测
1. 在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30° B.必有一个内角等于45°
C.必有一个内角等于60° D.必有一个内角等于90°
D
2.三角形的内角和等于( )
A.90° B.180° C.270° D.360°
B
当堂检测
3.在△ABC中,∠A=∠B+∠C,则下列对△ABC形状的判断正确的是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
4.若一直角三角形的两个锐角的差是20°,则较大
锐角的度数是________.
55°
B
当堂检测
5.已知:如图,AB∥CD,∠BEF,∠EFD的平分线相交于点G.求证:EG⊥FG.
证明:∵AB∥CD,
∴∠BEF+∠EFD=180°.
∵ EG,FG分别平分∠BEF,∠EFD,
∴ ∠GEF= ∠BEF,∠EFG= ∠EFD.
∴ ∠GEF+∠EFG= (∠BEF+∠EFD)=90°.
∴ ∠G=180°-(∠GEF+∠EFG)=180°-90°=90°,
即EG⊥FG.
当堂检测
6.在△ABC中,∠A= ∠B= ∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数.
解:∵∠A= ∠B= ∠ACB,
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°-90°-30°=60°.
∵CE是∠ACB的平分线,
∴∠ACE= ×90°=45°,
∴∠DCE=∠ACD-∠ACE=60°-45°=15°.
课堂小结
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
https://www.21cnjy.com/help/help_extract.php
7.5.1三角形的内角和定理(1)
第七章
平行线的证明
2021-2022学年八年级数学上册同步课件
学习目标
1.证明三角形内角和定理,并能运用这些定理解决简单的问题.
2.经历探索与证明的过程,进一步发展推理能力.
3.在一题多解、一题多变中,积累解决几何问题的经验,提升解决问题的能力.
导入新课
三角形家族的问题
不对!是我们钝角三角形的内角和最大!
我们锐角三角形的内角和度数最大!
你们别吵了!还是我们直角三角形的内角和最大!
讲授新课
三角形的内角和定理的证明
一
问题1:你觉得他们谁说的对
问题2:你还记得吗?小学我们是怎样探索三角形内角和的?
你能给大家说说或者展示一下吗?
讲授新课
一、测量法
480
720
600
600+480+720=1800
讲授新课
思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢
折叠
探究一:折叠的方法,和你们的操作一样吗?
二、折叠法
讲授新课
三、剪拼法(撕拼法)
A
B
C
2
1
讲授新课
A
C
B
A
C
B
E
旋转平移
问题1:如图,当∠A移到∠1的位置时,残边CD和边AB有何位置关系?为什么?
问题2:在剪拼法中,通过移动角拼成了一个平角;如果不实际移动角,那么你还有其它方法可以达到同样的效果吗
讲授新课
A
C
B
E
D
A
C
B
1
2
3
E
规范作图
辅助线
辅助线通常画虚线
辅助线
讲授新课
思路总结
添加辅助线
三角形内角和
转化
平角/同旁内角
讲授新课
知识要点
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
讲授新课
你还有什么方法可以达到同样的效果?
可以用“两直线平行,同旁内角互补”来说明.可以通过作辅助线实现移动的效果,例如延长BC到点D,过点C作射线CE∥BA,这样就相当于把∠A移到了∠1的位置,∠B移到了∠2的位置.这里的CD、CE称为辅助线,辅助线通常画成虚线。
讲授新课
想一想:还有其他方法证明三角形内角和定理吗?
讲授新课
已知:如图,在△ABC中.
求证:∠A+∠B+∠C=180°.
证明:(如图①)过点A作PQ∥BC,
则∠1=∠B,∠2=∠C
(两直线平行,内错角相等).
∵∠1+∠BAC+∠2=180°(平角的定义)
∴∠B+∠BAC+∠C=180°(等量代换).
讲授新课
已知:如图,在△ABC中.
求证:∠A+∠B+∠C=180°.
证明:(如图②)过点C作CE∥AB,
则∠1=∠A(两直线平行,内错角相等),∠B+∠BCE=180°
(两直线平行,同旁内角互补).
∵∠BCE=∠BCA+∠1,
∴∠B+∠BCA+∠1=180°(等量代换),
∴∠B+∠BAC+∠A=180°(等量代换).
讲授新课
已知:如图,在△ABC中.
求证:∠A+∠B+∠C=180°.
证明:(如图③)过BC边上的一点P作QP∥AC,RP∥AB,交AB于Q,交AC于R,
则∠1=∠B,∠2=∠C
(两直线平行,同位角相等).
∠A=∠BQP=∠QPR
(两直线平行,同位角相等,内错角相等).
∵∠1+∠2+∠QPR=180°(平角的定义),
∴∠A+∠B+∠C=180°(等量代换).
讲授新课
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
三角形的内角和定理的运用
二
讲授新课
【变式题】如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°-∠A-∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
讲授新课
例2 如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°-∠FEA-∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°-∠CFD-∠FCD=40°.
讲授新课
基本图形
由三角形的内角和定理易得∠A+∠B=∠C+∠D.
由三角形的内角和定理易得∠1+∠2=∠3+∠4.
总结归纳
讲授新课
例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°,
∠C为(x + 15)°, 从而有
3x + x +(x + 15)= 180.
解得 x = 33.
所以 3x = 99 , x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°.
几何问题借助方程来解. 这是一个重要的数学思想.
讲授新课
【变式题】在△ABC中,∠A= ∠B= ∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数.
解析:根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,∠ACD,最后根据角平分线的定义求出∠ACE即可求得∠DCE的度数.
比例关系可考虑用方程思想求角度.
讲授新课
解:∵∠A= ∠B= ∠ACB,
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°-90°-30°=60°.
∵CE是∠ACB的平分线,
∴∠ACE= ×90°=45°,
∴∠DCE=∠ACD-∠ACE=60°-45°=15°.
当堂检测
1. 在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30° B.必有一个内角等于45°
C.必有一个内角等于60° D.必有一个内角等于90°
D
2.三角形的内角和等于( )
A.90° B.180° C.270° D.360°
B
当堂检测
3.在△ABC中,∠A=∠B+∠C,则下列对△ABC形状的判断正确的是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
4.若一直角三角形的两个锐角的差是20°,则较大
锐角的度数是________.
55°
B
当堂检测
5.已知:如图,AB∥CD,∠BEF,∠EFD的平分线相交于点G.求证:EG⊥FG.
证明:∵AB∥CD,
∴∠BEF+∠EFD=180°.
∵ EG,FG分别平分∠BEF,∠EFD,
∴ ∠GEF= ∠BEF,∠EFG= ∠EFD.
∴ ∠GEF+∠EFG= (∠BEF+∠EFD)=90°.
∴ ∠G=180°-(∠GEF+∠EFG)=180°-90°=90°,
即EG⊥FG.
当堂检测
6.在△ABC中,∠A= ∠B= ∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数.
解:∵∠A= ∠B= ∠ACB,
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°-90°-30°=60°.
∵CE是∠ACB的平分线,
∴∠ACE= ×90°=45°,
∴∠DCE=∠ACD-∠ACE=60°-45°=15°.
课堂小结
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
